双无刷直流电机同步系统的仿真研究

王桂英，程向向

（沈阳农业大学信息与电气工程学院，辽宁沈阳110866）

1 引言

无刷直流电机结构简单，维护方便，运行可靠，体积小，寿命长，在伺服控制、计算机外围设备、数控机床、机器人等领域得以广泛的应用。在纺织、机器人手臂、印刷和单台电机不足以驱动负载等系统中，都需要双电机高精度同步控制，而同步控制算法的优劣将直接影响系统动静态性能和产品的质量。实际运行中，各传动轴的特性和外界负载扰动的变化都会降低系统的同步性能，达不到系统快速性，鲁棒性强的要求。因此，作为同步系统核心的同步控制算法成为研究的热点。

目前，采用主从同步控制方式将主电机转速作为从电机速度给定，系统稳定运行时同步性能好，但在电机启停时存在转速波动较大的问题且从电机负载扰动无法回馈给主电机，进一步降低了同步性能［3］。并行同步控制控制方式采用机械传动轴实现同步，性能较差，精度低；等状态耦合控制可以克服启停时性能差的问题，但只能适应于双电机的系统且耦合参数的选择比较复杂［3］。

在纺织工业等应用中常用到多台电机以一定的同步系数同步运行，为此，本文在单台电机仿真的基础上采用了偏差耦合控制方式，运用变论域自适应模糊PID控制算法（VUFPID）来实现双电机同步控制，通过仿真结果验证电机数学模型搭建的正确性和该算法在同步控制系统中的可行性。

2 单台无刷直流电机数学模型和建模

采用三相无刷直流电机，三相星形连接，两两导通的通电方式。为便于分析，假定：

（1）三相绕组完全对称，气隙磁场为方波，定子电流、转子磁场分布皆对称;

（2）忽略齿槽、换相过程和电枢反应等的影响；

（3）磁路不饱和，不计涡流和磁滞损耗［4］。

再结合BLDC的原理和特性，利用相变量法建立数学模型，列出电压方程、转矩方程和反电动势方程。

电压方程：

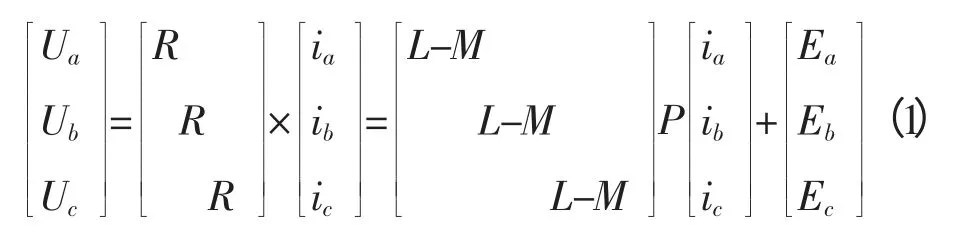
转矩方程：

其中：B为阻尼系数（N·m·s／rad）；J为转动惯量（kg·m2）；Te为电磁转矩（N·m），TL为负载转矩（N·m）,R为三相定子电阻；L为定子自感；M为定子互感；U为三相定子电压；E为三相反电动势；p为微分

反电动势方程：采用线性分段法表示三相反电动势［4］。

单台电机采用速度电流双闭环控制，其中速度环采用常规PID控制，考虑到积分饱和的影响，采用防积分饱和的PID模块，电流环采用电流滞环控制策略，使电流紧跟速度环输出的电流参考值。模型的建立如文献［2］、［4］。这些文献没有考虑到中性点的情况，虽然理想情况下三相定子电流之和0，但由于换相等原因造成电流波动的幅度依然很大，本文将每相定子电流减去三相电流和的1/3来作为每相电流实现模拟中性点。文献［4］提出的采用线性分段法表示三项反电动势会造成转矩波动等问题，本文在此基础上提出每相电压减去三相电压和的1/3作为每相电压输入。

3 双无刷直流电机同步控制系统设计与建模

3.1 系统总体结构

偏差耦合控制的思想是将一台电机转速反馈与其他电机的转速反馈分别作差，再将偏差相加经过算法运算后作为当前电机的速度补偿[11]。本文考虑两台电机，同步系数设为λ1与λ2，电机转速满足当均为1时转速比为1∶1，跟随误差为补偿控制器1和2中用PI控制器做前馈控制，旨在消除因负载波动较大，电机参数不同造成的同步误差与速度波动大的影响，因为任意一台电机速度波动对另一台造成干扰，而PI控制器能够在控制量发生变化之前产生作用，按一定规律快速消除跟随误差，在满足同步性能同时，提高系统动静态性能。如图1所示为偏差耦合同步控制结构图。

图1 偏差耦合同步控制结构图

3.2 变论域自适应模糊PID算法

PID控制算法简单，鲁棒性好，理论体系较为成熟，在工业控制中得到了广泛的应用，但对于BLDC这种非线性、强耦合的时变系统来说，PID的参数难以确定，需要丰富的经验，且参数一经确定，运行中无法更改［1］。因此，限制了常规PID控制在同步系统中的应用。针对这些复杂的系统，可以用自适应模糊PID控制来替换常规PID来进行速度补偿。模糊控制不需要具体了解受控对象的数学模型，以系统偏差和偏差变化率作为输入来实现工业控制。模糊PID由参数模糊化、模糊规则推理、解模糊化和PID控制实现，将系统偏差n*与偏差变化率nc作为输入，通过量化因子将基本论域转化到模糊论域并经过推理，解模糊，比例因子得到实际的输出值给被控对象。一般为了实现PID参数的自整定，将PID中kp、ki和kd的变化量Δkp、Δki和Δkd作为模糊控制器的输出。采用三角函数作为隶属度函数，输入、输出论域模糊集均为[-6,6]，模糊语言值{NB，NM,NS，Z，PS，PM，PB}，模糊规则表如表1所示。

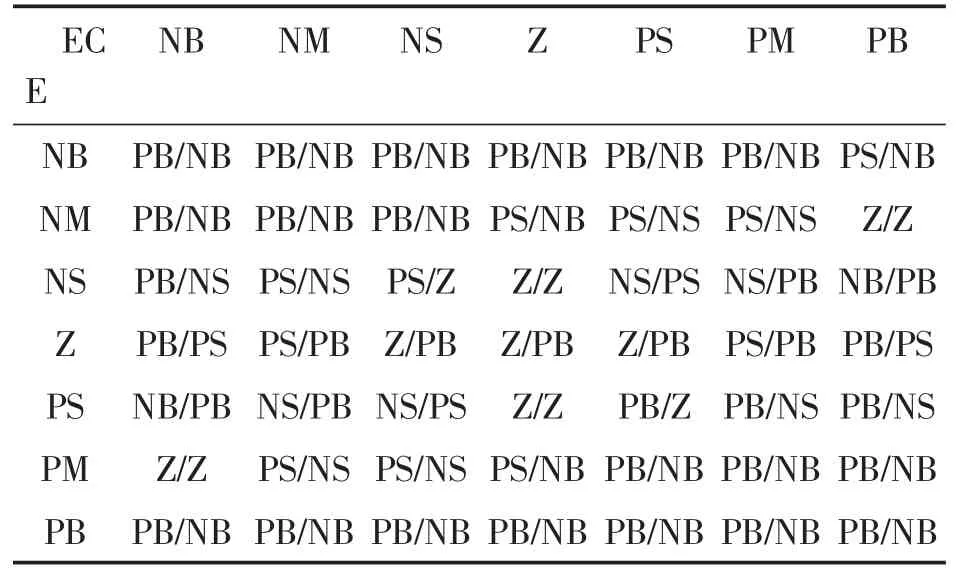
表1 Δkp、Δki的模糊控制规则表

误差较小时，PID具有调节速度快的优点，而模糊控制是分档处理，在误差较大时，具有明显优势，消除稳态误差能力较弱。一般希望在大范围内调速时要求快速性，在小范围误差内实现精调，VUFPID在自适应模糊PID控制的基础上引入了伸缩因子，使基本论域的划分发生改变，在适当时刻合理地划分来提高控制性能［7］、［9］。论域调整规则为：放大量化因子相当于收缩输入论域,缩小量化因子相当于扩大输入论域;缩小比例因子相当于收缩输出论域,放大比例因子相当于扩大输出论域。而关键就在于怎样确定论域伸缩的合理机制,即确定适当的伸缩因子,使最终的控制效果能够最大限度满足要求,常用选择基于函数型的伸缩因子［7］。

对于输入论域，选择函数为：

输出论域选择函数为：

伸缩因子选择基于论域调整规则和PID参数对性能的影响即kp与kd与误差具有一致性，而ki与误差具有单调反向性［6］。

3.3 系统建模

本文中两台电机结构参数相同，均采用转速电流双闭环控制策略，仿真模型包括电机本体模块、速度给定模块、偏差耦合控制模块、速度补偿模块、补偿输出模块等。单台电机模块运用Matlab/Simulink的封装功能封装成bldc1和bldc2。如图2所示为同步控制仿真模型。图2中补偿输出模块采用Matlab中S函数来编写，以速度补偿作为输入，输出回馈给各电机，bldc1为正反馈，bldc2为负反馈。该模块主要减小调节时间和当误差较小时的震荡，输出功能的程序如下：

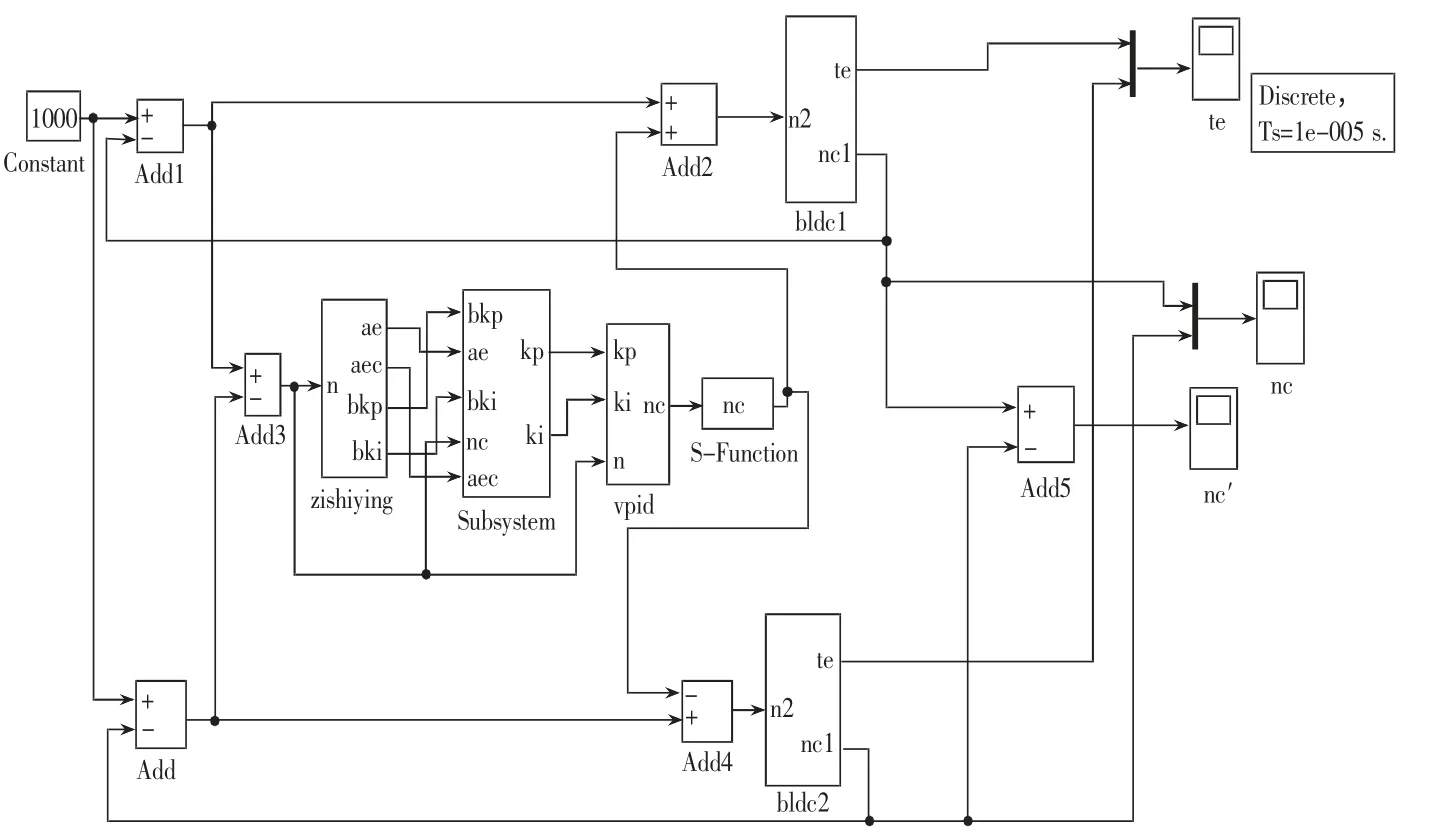
图2 同步控制仿真模型

4 仿真结果与分析

本例选择两台同参数的BLDC，参数如下：电子电阻4.765Ω，阻尼系数0.008N·m·s／rad，定子电感0.008H，励磁磁通0.1848Wb，极对数1，额定电压220V，额定转矩30N·m，转速给定1000rpm，0.035s时给BLDC1大小为10N·m的扰动。在PID参数整定时，由于微分环节延长了调节时间，而且无法用DSP来实现，本文中舍掉微分环节，选择速度环kp=10，ki=0.15，电流环上限为0.3A，下限为0.1A，防积分饱和限幅0.98。

在同步系统中，根据实际需求，选取误差范围n*为[-15,15]rpm，误差变化率范围nc为[-150,150]r/min/s，选择kp=2，变化范围[1,3]；ki=5，变化范围[1,10]。模糊控制器中量化因子分别为0.4,0.04，比例因子为0.16,0.83。VUFPID的转速差伸缩因子：1－0.5exp（－0.4e2），转速差变化率的伸缩因子：1－0.5exp（－0.4e2），比例作用的伸缩因子：积分作用的伸缩因子：

仿真使用步长可变的Runge-Kuttasuanfa算法，运行上述模型得到常规PID，自适应模糊PID，变论域自适应模糊PID分别作为速度补偿器得到的转速曲线如图3所示。

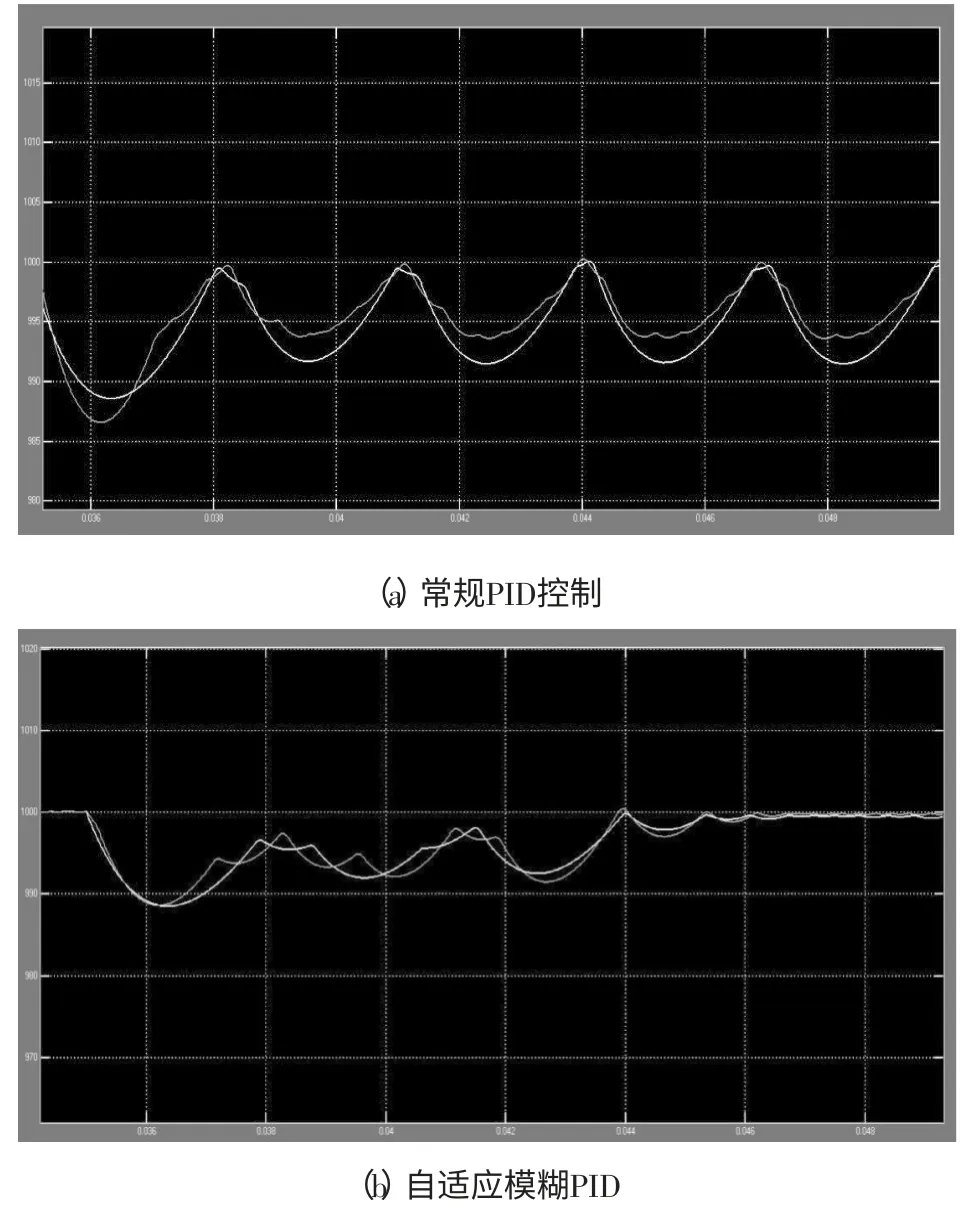
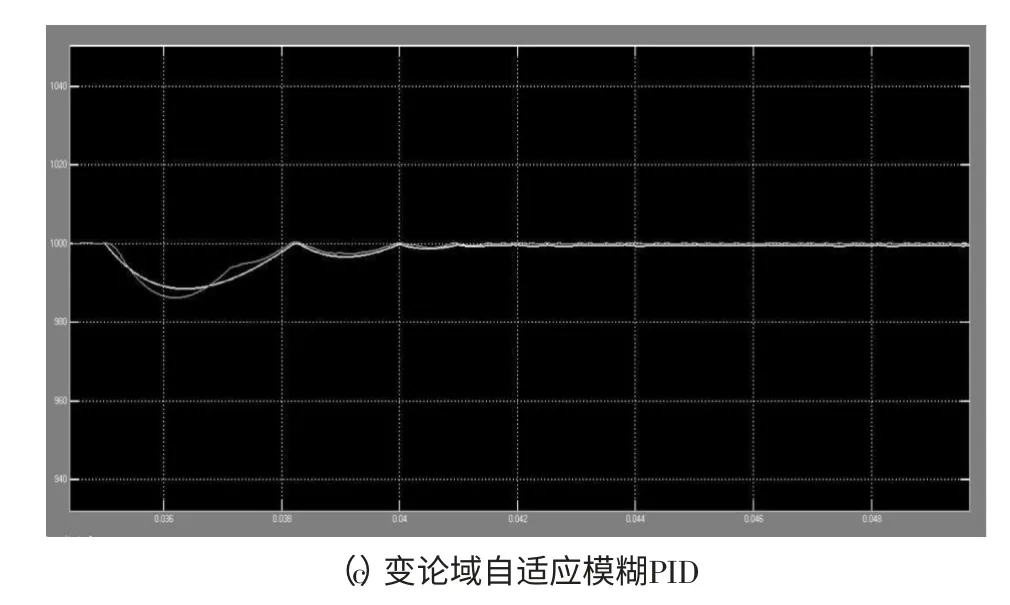
图3 局部放大后的转速曲线

3种控制策略转矩输出曲线如图4所示，图3（c）中bldc2在0.035s突加5N·m的负载扰动,bldc1不变。

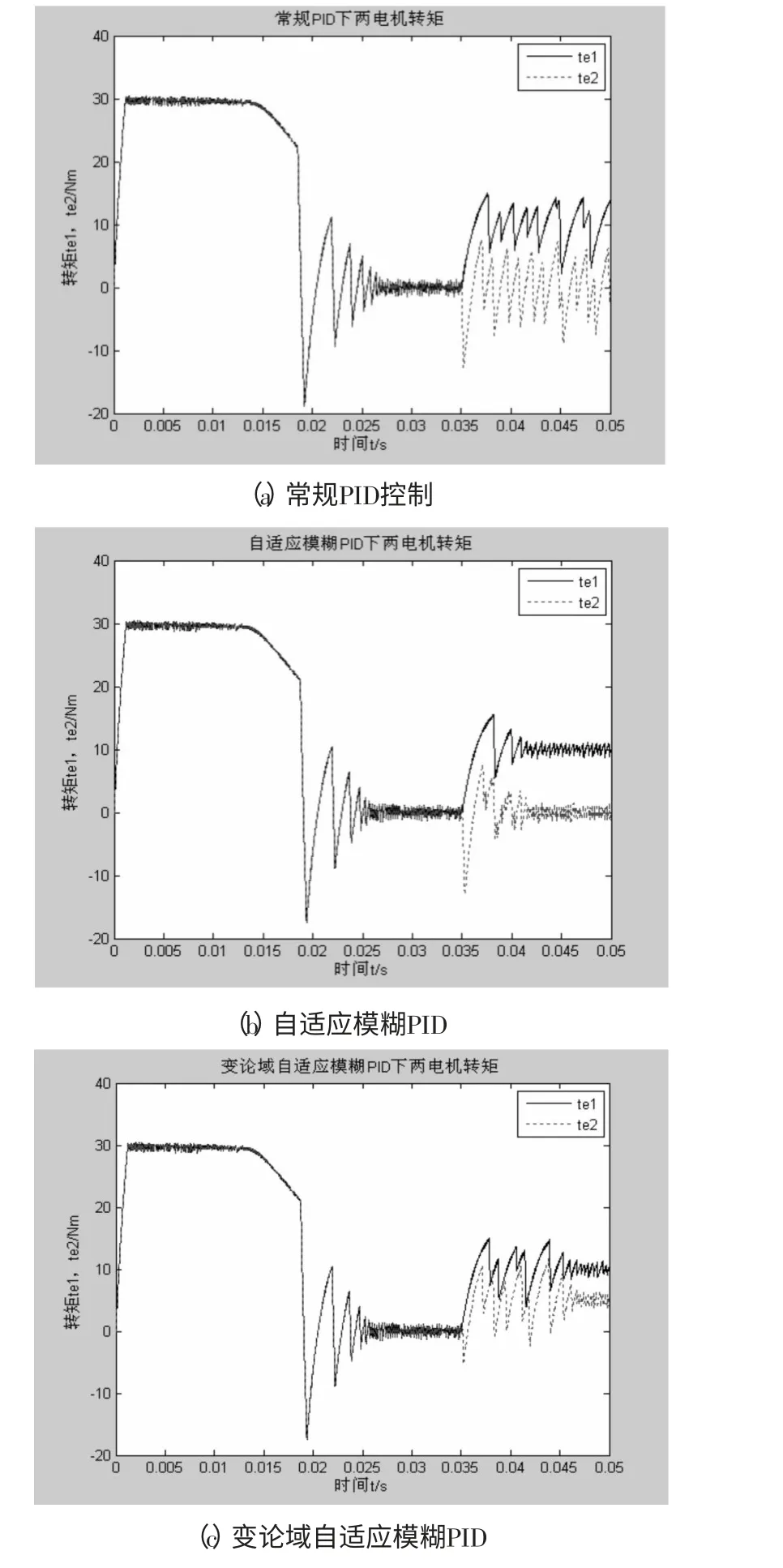
图4 转矩输出曲线

局部放大后的相电流波形如图5所示，电流波形较为理想,与分析的矩形波一致,验证了BLDC模型建立的准确性。

图5 一相局部放大后电流波形

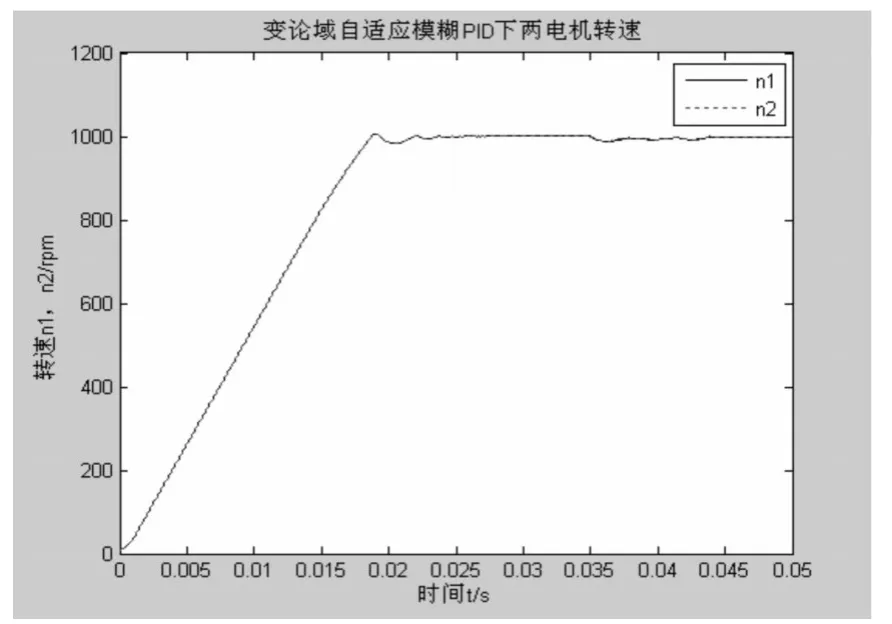
图6 转速输出曲线

从图3和图4波形可以看出遇到负载扰动时,3种控制策略都出现不同程度转速波动和转矩波动,如表2所示，为3种策略下遇扰动后参数比较。

表2 3种策略下遇扰动后参数比较

由此得出VUFPID控制器较常规PID和自适应PID控制器更好的转速跟随性能，扰动后超调更小，转矩波动更小，虽然转矩的调节时间较自适应PID控制策略长，但转矩跟随性能较好。

5 结束语

本文将基于函数的伸缩因子引入到自适应模糊PID控制器中，使模糊论域自适应伸缩，组成变论域自适应模糊PID控制器，进而作为偏差耦合控制的速度补偿器应用于双无刷直流电机同步控制系统中。仿真结果表明，相比较于常规PID和自适应模糊PID控制，在快速性、抗干扰性、转矩波动方面等方面得到了改善，负载扰动后速度波动范围小，调节时间更短，验证了该方法的可行性。为无刷直流电机采用DSP来实现在纺织、机器人等精度要求高、抗扰性能高的场合的应用提供了一种解决方案。

［1］席爱民.模糊控制技术［M］.西安：西安电子科技大学出版社，2008.6.

［2］洪乃刚.电力电子，电机控制系统的建模和仿真［M］.北京：机械工业出版社，2010.

［3］张 良，于海生，刘华波等.基于模糊－PID控制的主从电机同步传动系统［J］.电气传动自动化，2008，30（5）：34－37.

［4］殷云华，郑 宾，郑浩鑫.一种基于Matlab 的无刷直流电机控制系统建模仿真方法［J］.系统仿真学报，2008，20（2）：293－298.

［5］Teck－Seng Low，Tong－Heng Lee，King－Jet Tseng，Kai－Sang Lock.Servo performance of a BLDC drive with instantaneous torquecontrol［J］.IEEE TransactionsonIndustryApplications，1992，28（2）.

［6］许 宏，李乐宝，张 怡等.变摩擦负载下双电机同步控制系统设计与实验［J］.中国机械工程，2011，22（24）：2908－2913.

［7］李红伟.变论域模糊控制的无刷直流电机控制系统［J］.控制工程，2010，17（5）：599－602.

［8］夏长亮，方红伟.永磁无刷直流电机及其控制［J］.电工技术学报，2012，27（3）：25－34.

［9］孙 怡.基于模糊PID控制的多电机同步控制系统的研究［D］.／王庆明：华东理工大学，2012.

［10］尹达一，黄玉婷，刘云芳.基于MATLAB／Simulink的双电机速度跟踪伺服系统仿真［J］.中国惯性技术学报，2011，19（2）：229－233.

［11］杨晨娜，张 怡.双电机同步控制系统的设计与仿真［J］.工业控制计算机，2009，22（1）：36－37.