基于傅里叶级数展开的纵波方位各向异性裂缝预测
王康宁,孙赞东,侯昕晔
(1.中国石油大学(北京)地质地球物理综合研究中心,北京102249;2.中国石油化工股份有限公司石油勘探开发研究院,北京100083;3.中国石油天然气集团东方地球物理勘探有限责任公司,河北涿州072751)
基于傅里叶级数展开的纵波方位各向异性裂缝预测
王康宁1,2,孙赞东1,3,侯昕晔1
(1.中国石油大学(北京)地质地球物理综合研究中心,北京102249;2.中国石油化工股份有限公司石油勘探开发研究院,北京100083;3.中国石油天然气集团东方地球物理勘探有限责任公司,河北涿州072751)
利用地震反射纵波的方位各向异性信息预测地下裂缝的发育和分布情况一直是地球物理学家研究的热点课题,常规方法是使用两项Ruger线性近似公式反演得到裂缝相对密度和走向,其计算结果存在多解性且只能计算入射角较小的情况。对任意对称面各向异性介质的纵波方位各向异性弱反射系数近似公式进行整理,结合Schoenberg线性滑移理论,得到纵波方位各向异性反射系数近似公式的傅里叶级数展开公式,给出了基于傅里叶级数展开的纵波方位地震数据裂缝预测方法。将该方法应用于辽河油田雷家地区沙河街组白云岩储层的裂缝预测,并与常规各向异性反演结果及实际成像测井数据进行对比,验证了方法的有效性。研究结果表明,该方法计算简单且不受入射角度的限制,预测的裂缝相对密度与常规反演方法预测的结果精度近似,与成像测井资料吻合,故可作为传统方法的验证和补充。
裂缝预测;傅里叶级数;各向异性;沙河街组;白云岩储层
天然裂缝对油气的运移和聚集有着重要的意义,因此裂缝预测逐渐成为油气勘探开发中越来越重要的研究领域。目前裂缝预测的技术主要包含两大类:一是基于叠后数据的断裂检测技术,在宏观上间接地反映裂缝发育情况;二是基于叠前地震数据根据各向异性原理预测裂缝发育程度。后者由于其预测结果的直观性以及随着地震数据处理能力的不断发展,已引起越来越多学者的重视。
含有裂缝的储层是典型的各向异性介质,自20世纪70年代以来,地震勘探中的各向异性研究发展迅速。其中Crampin提出了方位各向异性和横波分裂等概念,极大地推动了各向异性技术的发展[1-2];Thomsen[3-4],Hudson[5-6],Schoenberg等[7-9]先后提出了不同的理论模型,对该技术的发展做出了重要的贡献;而Ruger提出的近似方程[10]大大地推动了纵波振幅方位各向异性反演技术的发展,利用纵波振幅随着地震观测方位变化的信息来预测裂缝成为当下最常用的裂缝检测技术。但目前基于Ruger方程的叠前裂缝反演方法具有以下一些缺陷:①根据Ruger方程所求得的各向异性参数无法确定符号,导致裂缝方位具有多解性[11];②在方程求解的过程中舍弃了高次项,得到的解是在入射角较小情况下的近似解。因此,纵波振幅方位各向异性反演技术仍具有较大的改进空间,需要进行深入的探索。国外已有学者提出利用傅里叶技术分析纵波方位反射系数的思路[11-12],本文根据这一思路,利用三角函数变换公式对任意对称面各向异性介质的纵波方位各向异性弱反射系数近似公式进行整理,得到纵波方位各向异性反射系数近似公式的傅里叶级数展开公式,探索了利用傅里叶级数预测裂缝的具体实现方法。
1 方法原理
随观测方位发生变化的纵波反射系数序列可以视为周期为2π的函数,并表示成傅里叶级数的形式[11,13]:
(1)
式中:φ为方位角;a0,an,bn(n=1,2,…)为常数。
(1)式也可以用三角函数正交集表示:
(2)
其中,r0为常数,每一项的振幅和相位分别如下:
(3)
(4)
由于纵波地震数据关于共中心点对称,纵波方位各向异性反射系数的近似方程可以被看作偶谐函数,因此其傅里叶级数展开式只包含偶次谐波分量,如图1所示[12]。
由于各向异性佐普里兹方程物理上的非直观性和数学形式上的复杂性,研究者提出很多描述纵波方位各向异性反射系数的近似方程,但目前在裂缝反演研究中最常用到的是Ruger线性近似方程。本文通过对任意对称面各向异性介质的纵波弱反射系数近似公式[14]进行整理,结合Schoenberg线性滑移理论模型(见附录A)[15-16],给出纵波方位各向异性反射系数近似公式的傅里叶级数展开式:
(5)
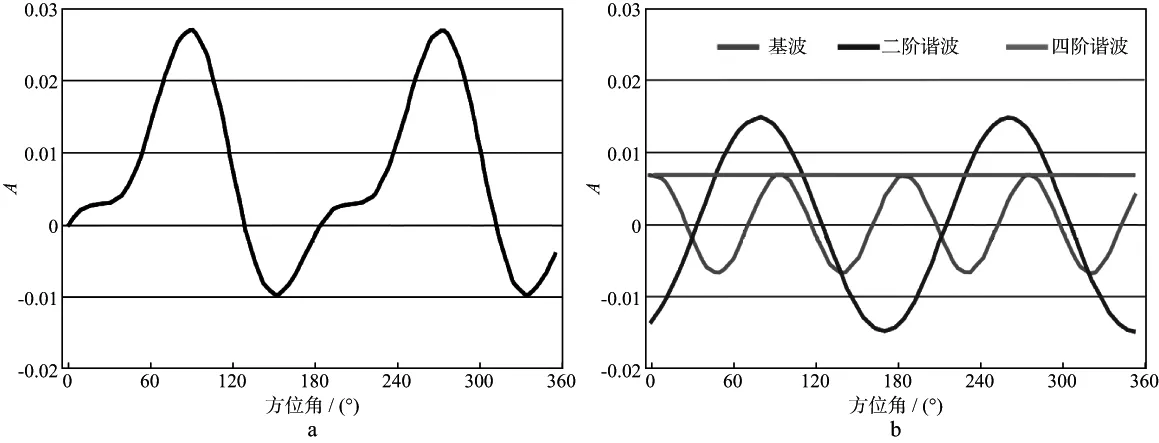
图1 固定入射角振幅随方位角变化特征(a)以及傅里叶级数分解结果(b)
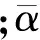
(6)
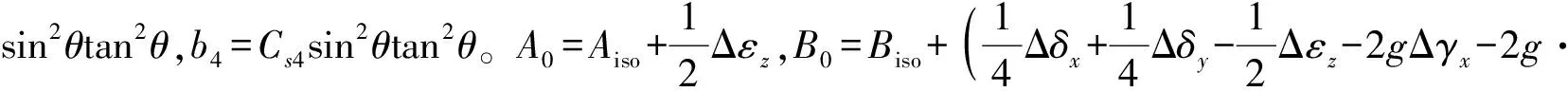

其中D为Schoenberg线性滑移理论模型中的刚度矩阵,而当各向异性介质为斜方晶体或者其它可以用9个以下独立弹性常数表征的晶体时,以下几个参数为0:
(7)
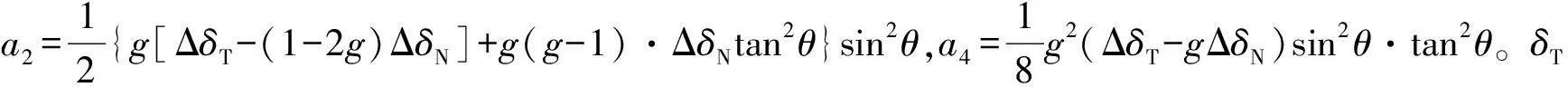
由此可知,根据Pšencǐk线性近似方程整理的傅里叶级数表达式最高次的傅里叶级数n=4项。而完整的各向异性佐普里兹方程表示的纵波反射系数函数并非只包含四阶以下的傅里叶级数,其包含的级数越多,各向异性佐普里兹方程的近似程度就越高,对各向异性参数的描述越准确。但是在实际数据的计算中,四阶以上的傅里叶级数往往会因受到噪声的严重干扰而被舍去[12];同时,傅里叶级数展开方法要求分方位偏移数据的方位角采样间隔必须满足尼奎斯特采样定理[11]。
我们通过傅里叶级数形式的纵波方位各向异性线性近似公式与常规反演方法对比,阐述了傅里叶级数方法预测裂缝的可行性。常规各向异性反演方法通常使用Ruger近似方程,并且为了便于计算,当入射角较小时,方程的高次项一般被舍弃,进一步简化为两项Ruger公式:
(8)
其中,Bani为描述地层各向异性程度的参数,通常被近似认为是地层裂缝发育密度。根据Ruger方程中Bani的计算公式[10]以及Thomsen参数的定义[5-6],结合Schoenberg裂缝介质理论模型,可以得到各向异性参数Bani的近似公式:
(9)
因此(7)式中傅里叶级数的二阶展开式可改写为[11]:
(10)
2 实例研究
为了验证基于傅里叶级数展开的裂缝预测方法的有效性,将该方法应用于辽河油田雷家地区沙河街组白云岩储层裂缝预测研究,同时,用基于两项Ruger方程的各向异性线性反演方法对比验证上述方法的有效性和精度。
2.1 研究区地质概况
辽河油田西部凹陷雷家地区古近系沙河街组沙四段广泛发育以泥质白云岩为主的致密储层,目的层生油及封盖条件良好,油气显示极为丰富。由于该区沙四段具有极低孔、低渗的致密储层特征,且储层厚度变化大、非均质性强,因此开发效果不均衡,大部分井只见油气显示和低产油气流,自然产能低,高产井很少,主要依靠压裂措施增加产量。图2显示了该地区白云岩主要储集空间类型,岩心观察发现研究区致密油藏裂缝发育,裂缝类型包括微裂缝、穿层缝、层内缝和顺层缝,其中大部分裂缝产状为高角度裂缝。裂缝发育程度与岩性关系密切,含白云质越高的岩石越容易产生裂缝。研究发现,各种类型的裂缝是该区致密储层主要的储集空间及渗流通道,单井产量与裂缝发育程度密切相关,裂缝预测研究对这种非常规致密油藏的开发具有重要意义。

图2 沙四段泥质白云岩储集空间特征
2.2 方法应用与效果对比
对本区地震观测系统进行分析和试验之后,选取6个方位角范围进行分方位筛选,从而得到平均方位角分别为90°,106°,122°,138°,154°,170°的6个方位角共中心点道集(表1),对其进行叠前时间偏移处理得到各向异性反演所需要的不同方位CRP道集。在方位角分析过程中,发现单个CDP的覆盖次数较低,为了有效压制噪声,处理过程中应用了超道集技术,将面元由25m×25m扩大到50m×50m(图3)。该技术的应用牺牲了一定的横向分辨率,但是提高了方位各向异性反演的准确性。同时,为使每个方位的地震覆盖次数较为均匀,在预处理时舍弃了较小和较大偏移距数据。

表1 研究区地震资料方位角划分方案

图3 方位角划分方案(a)及面元扩大(b)
针对6个分方位地震纵波数据,分别进行了基于Ruger方程的常规各向异性反演和基于傅里叶级数展开的裂缝相对密度计算。在应用常规Ruger各向异性反演方法的过程中,为了提高反演精度并压制噪声,使用了30°角以内的全部入射角道集数据来求取超定解,因此得到的结果是该方法所能求得的精度最高解。傅里叶级数展开方法由于算法自身的原因,只能选取某一个入射角数据进行分析,经过对比研究,优选了26°~34°的入射角道集数据进行了部分角度叠加,最终使用平均角度为30°的数据计算裂缝相对密度。
研究区内雷88井实钻揭示目的层为裂缝型泥质白云岩储层,试油结果显示较好,初期试采产油24t/d。该井电阻率成像测井(FMI)显示单组裂缝发育,具备地震各向异性响应的地质基础。应用基于Ruger方程的常规反演方法和傅里叶级数展开方法计算过雷88井地震剖面的各向异性强度,采用FMI成像测井数据标定预测结果,发现各向异性参数Bani高值区域对应雷88井裂缝发育层段,验证了方法的可行性(图4)。对比图4a和图4b 可见,两种方法均能在整体上有效预测白云岩储层各向异性展布特征,且傅里叶级数展开方法明显较好地消除了一些各向异性反演中出现的噪声。
雷77井为研究区内另一口高产井,钻遇火山角砾岩储层,FMI成像测井显示高角度裂缝非常发育。应用上述两种方法计算过雷77井地震剖面各向异性强度,发现两种方法在井点处的裂缝各向异性强度预测结果较为一致,均符合实钻FMI成像测井解释的裂缝发育情况(图5)。两种方法反演的地层各向异性规律基本一致,只是在分辨率和信噪比上有所差别,其中傅里叶级数展开法预测的各向异性体空间展布范围较常规Ruger方程法预测范围小,更接近火山岩储层地质认识。

图4 过雷88井地震剖面不同反演方法计算的各向异性强度与成像测井资料对比
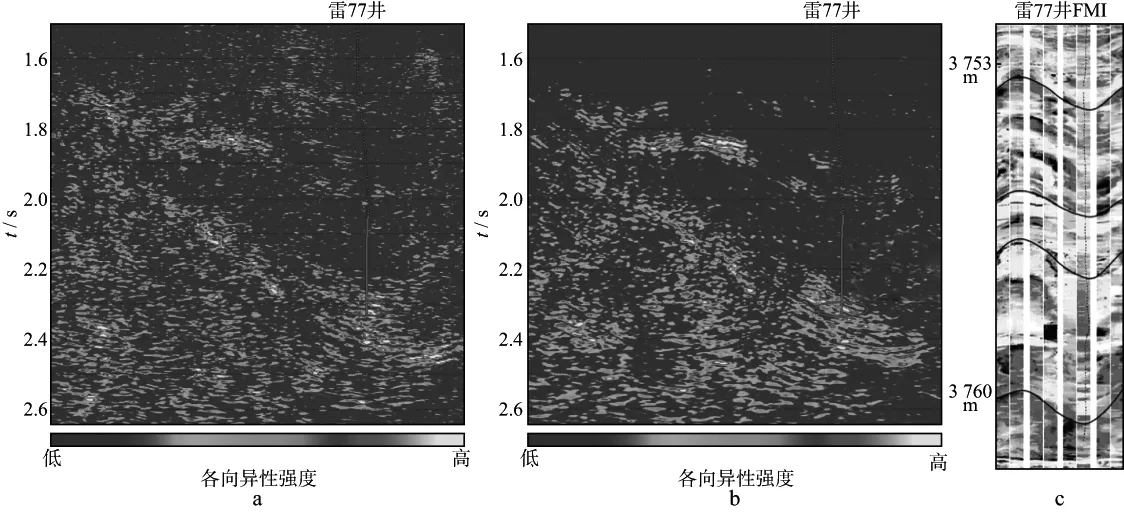
图5 过雷77井地震剖面不同反演方法计算的各向异性强度与成像测井资料对比
3 结束语
本文研究结果显示,纵波方位各向异性反射系数的近似公式可以合理地展开为傅里叶级数的形式,利用级数的二阶项系数可以直接近似估算地层的各向异性强度,进而预测地层裂缝相对密度。该方法预测精度与常规反演方法近似,故可作为传统方法的验证和补充。
由于傅里叶级数的系数全部为正数,本文方法与常规方法一样无法得到裂缝走向的唯一解。如果使用完整的傅里叶展开式,利用多个入射角、多个方位角的纵波反射数据进行非线性反演,则可以准确地得到裂缝方位,解决Ruger方程等传统方法的多解性问题,这将成为本文进一步的研究目标。
致谢:感谢中国石油天然气股份有限公司辽河油田分公司提供的各种资料与支持;感谢中国石油大学(北京)地质地球物理综合研究中心提供的良好硬件设施与研究条件。
[1] Crampin S.A review of wave motion in an anisotropic and cracked elastic media[J].Wave Motion,1981,3(4):343-391
[2] Crampin S.Evaluation of anisotropy by shear-wave splitting[J].Geophysics,1985,50(1):142-152
[3] Thomsen L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954-1966
[4] Thomsen L.Elastic anisotropy due to aligned cracks in porous rock[J].Geophysical Prospecting,1995,43(6):805-829
[5] Hudson J A.Wave speeds and attenuation of elastic waves in material containing cracks[J].Geophysical Journal International,1980,64(1):133-150
[6] Hudson J A.A higher order approximation to the wave propagation constants for a cracked solid[J].Geophysical Journal of the Royal Astronomical Society,1986,87(1):265-274
[7] Schoenberg M A.Reflection of elastic waves from periodically stratified media with interfacial slip[J].Geophysical Prospecting,1983,31(2):265-292
[8] Schoenberg M,Douma J.Elastic wave propagation in media with parallel and alligned cracks[J].Geopysical Prospecting,1988,36(6):571-590
[9] Schoenberg M,Sayers C.Seismic anisotropy of fractured rock[J].Geophysics,1995,60(1):204-211
[10] Ruger A.Variation of P-wave reflectivity with offset and azimuth in anisotropic media[J].Geophysics,1998,63(3):935-947
[11] Downton J.Azimuthal Fourier coefficients:a simple method to estimate fracture parameters[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011,269-273
[12] Roure B,Downton J,Doyen P M,et al.Azimuthal seismic inversion for shale gas reservoir characterization[J].Expanded Abstracts of 6thInternational Petroleum Technology Conference,2013,17034
[13] 乐正友.信号与系统[M].北京:清华大学出版社,2004:117-121 Le Z Y.Signals and systems[M].Beijing:Tsinghua University Press,2004:117-121
[14] Pšencǐk I.Properties of weak contrast PP reflection/transmission coefficients for weakly anisotropic elastic media[J].Studia Geophysica et Geodaetica,2001,45(4):176-199
[15] Backus G E.Long-wave elastic anisotropy produced by horizontal layering[J].Journal of Geophysical Research,1962,67(11):4427-4440
[16] Hsu C J,Schoenberg M.Elastic waves through a simulated fractured medium[J].Geophysics,1993,58(7):964-977
附录A
Schoenberg假设裂缝之间具有不连通性以及裂缝具有旋转不变性,提出了线性滑移裂缝理论,给出了在这种假设模型下的裂缝刚度矩阵和柔度矩阵的表达式。其与Hudson理论的最大区别是:Schoenberg理论用柔度参数Z和柔度矩阵S对裂缝介质进行描述,而Hudson理论用刚度矩阵C描述裂缝介质。下面对Schoenberg线性滑移裂缝理论进行介绍。
Backus引入了柔度矩阵(即刚度矩阵C的逆)对各向同性背景下的平行薄裂缝进行描述:
S=Sb+Sf
(A1)
其中,Sb是各向同性背景岩石的柔度矩阵,Sf是裂缝的柔度矩阵。
对于垂直平行薄裂缝,柔度矩阵Sf为:
(A2)
其中,ZN,ZV,ZH,ZNH,ZNV,ZVH是描述位移与应力关系的柔度矩阵元素。
对于最简单的旋转不变性裂缝,柔度矩阵的元素满足:
(A3)
令ZV=ZH=ZT,则公式(A2)中的柔度矩阵变为:
(A4)
其中,ZN为法向柔度参数,ZT为切向柔度参数。
对于完全各向同性背景模型,假设其拉梅系数为λ和μ,Hsu和Schoenberg引入无量纲参数:
(A5)
并称δN为法向弱度,δT为切向弱度。
通过求解柔度矩阵的逆,则等效裂缝介质的刚度矩阵为:
(A6)
刚度矩阵的密度标准化矩阵为:
(A7)
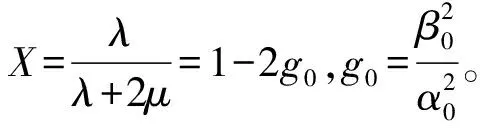
(编辑:戴春秋)
Fracture prediction by P-wave azimuthal anisotropy based on Fourier series decomposition
Wang Kangning1,2,Sun Zandong1,3,Hou Xinye1
(1.LabortaryforIntegrationofGeology&Geophysics,ChinaUniversityofPetroleum,Beijing102249,China; 2.SinopecPetroleumExploration&ProductionResearchInstitute,Beijing100083,China; 3.BGP,CNPC,Zhuozhou072751,China)
The application of anisotropic information of seismic reflection wave amplitude in underground fracture development and distribution prediction has always been a hot subject in geologists’ study.The conventional method,which adopts Ruger’s two-term linear formula to inverse the relative density and direction of fractures,obtains non-unique solutions and can only be applied with small incidence angles.To improve the method,the approximate formula of P-wave weak reflection coefficient varying with incidence-angle and azimuth-angle in arbitrary symmetric anisotropy media was rearranged.Based on the Schoenberg’s linear slip theory,the Fourier series expansion of P-wave azimuthally anisotropic reflection coefficient approximate equation is obtained.The Fourier series expansion of P-wave seismic data with different azimuth was applied in fracture prediction.It is applied in dolomite reservoir fracture prediction in Shahejie Formation,Liaohe Oilfield.The method is proved to be effective and reliable by comparison on the results with the conventional anisotropic inversion method and actual FMI data.The study shows that the method is simple in calculation and is not limited by the range of incidence angle.Meanwhile,the prediction accuracy of fracture density is close to conventional inversion method and the result agrees well with the FMI data.
fracture prediction,Fourier series,anisotropy,Shahejie formation,dolomite reservoir
2015-02-03;改回日期:2015-07-29。
王康宁(1986—),女,博士,主要从事地震反演及储层预测研究工作。
中国石油天然气股份有限公司科技重大专项子课题“深层地震资料保幅处理与叠前储层描述新技术”(2014E-3204)资助。
P631
A
1000-1441(2015)06-0755-07
10.3969/j.issn.1000-1441.2015.06.014

