快递公司协同车辆路径问题的优化

黄何列 蔡延光 汤雅连

(广东工业大学 自动化学院，广州 510006)

电子商务的快速发展离不开快递服务的支撑和带动。70%以上的网络购物，依靠快递完成交易过程。快递围绕着“物品传递”这一核心，把商家、消费者和电商平台，紧密地联系在一起。而且随着电子商务的发展，商品包裹的比重越来越大，全国快递业必将出现各大集团营运网络大规划和大整合的发展趋势。

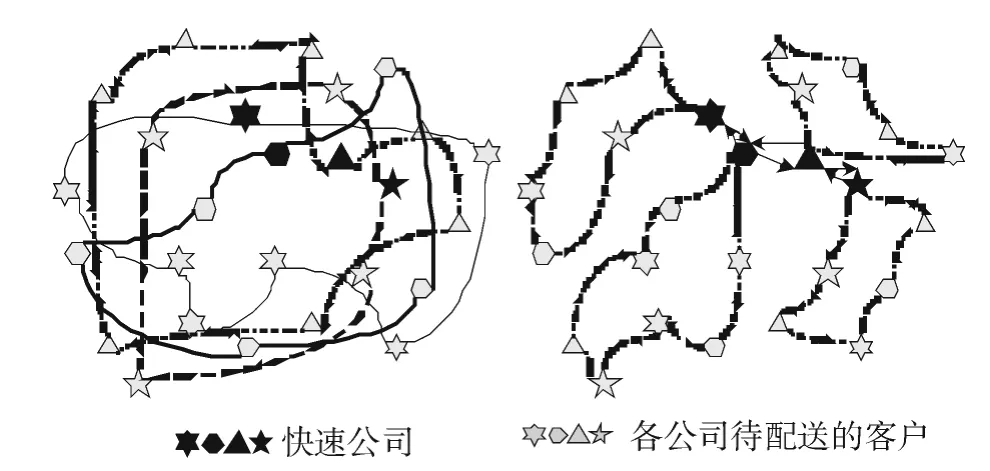
图1 快递公司协同配送的示意图 (4家快递公司和22个客户)

车辆路径问题 (Vehicle Routing Problem，VRP)［1］自1959年Dantzig和Ramser首先提出以来就引起了人们的高度重视。VRP的实用性强，应用广泛。所谓快递公司中多车场协同车辆路径问题 (multidepot collaborative vehicle routing problem，MDCVRP)可以这样描述:相邻的几家快递公司都有各自的车场，为该区域的多个客户配送货物，整合客户需求以及充分利用各快递公司的车队及人力资源，在满足所有客户需求的前提下，选择合理的配送路线进行协同配送，最小化配送成本。MDCVRP是MDVRP的延伸，快递公司协同配送的示意图如图1所示。不同快递公司之间协作运营，共同完成任务，MDCVRP与MDVRP的不同点在于MDCVRP包含了协同策略。

目前，许多学者对MDVRP进行了广泛研究。M.Mirabi等人［2］应用混合的启发式算法求解MDVRP，通过确定性、随机性和模拟退火机制来改进算法，仿真证明该算法优于现存的其他启发式算法;B Yu等人［3］应用融合了粗粒度并行策略、蚁群均衡策略和变异操作的改进ACO对MDVRP求解，建立一个虚拟的中心车场，将MDVRP转化为多个以虚拟中心车场为源节点的VRP问题;Yiyo Kuo等人［4］应用可变邻域搜索算法求解带负载成本的MDVRP，首先应用随机方法产生初始解，其次随机产生4个算子搜索邻域解，最后采用模拟退火机制接受邻域解;Andrea Bettinelli等人［5］应用分支定界定价算法求解带时间窗的多车型多车场MDVRP;Surekha P等人［6］应用GA求解MDVRP，首先基于距离分组将客户分配给最近的车场，然后应用C－W节约算法构建路径，最后应用遗传算法对其进行优化。目前，对协同车辆路径问题 (collaborative vehicle routing problem，CVRP)的研究不是太多。温惠英等人［7］建立以车辆配送总费用最小为目标的一类带时间窗协同车辆路径问题数学规划模型，采用自适应离散粒子群算法求解;之后，温惠英等人［8］又考虑了车辆行驶时间和顾客服务时间的不确定性，建立了带时间窗协同车辆路径问题模糊规划模型;张文静等人［9］利用协同粒子群算法来解决MDVRP，通过真正的全局最优值来更新个体速度，同时每个子群体又采用不同的速度进化方式来保持解得多样性，避免陷入局部最优;孙博等人［10］研究了3种类型的CVRP，研究表明随着车辆任务可靠度的增大，物流配送方案费用将可能越高，但该方案的可靠性较好，故它在物流实际配送中受不确定性的干扰较小;之后，孙博等人［11］又研究了一类属于不同公司的配送中心共享车队、仓储等资源为客户协同配送货物的协同车辆路径问题;刘冉等人［12］研究了面向协同运输的多企业利益分配问题，采用Shapley值法对协同的利益进行合理分配。但是综合MDVRP和CVRP两种问题模型的研究还没发现，所以研究MDCVRP具有非常重要的意义。

1 问题描述及数学模型

1.1 问题描述

快递配送中的MDCVRP是指多家快递公司的车辆从该公司所属车场出发，可以将货物送到其他快递公司，由其他公司配送，也可以自行配送。各个公司所配备车场的车辆数量充裕，有多辆不同类型的车。组织适当的配送计划及行车路线，在满足一定的约束条件下 (客户需求量、车辆载重、时间窗等)，实现目标的最优化 (成本最小、车辆最少等)，提高客户满意度，不考虑装卸货时间。

1.2 数学模型

优化模型符号如下:

客户编号:，i=1，2，…，l 到达客户i的时间:Tai

客户i的需求量:gi(i=1，2，…，l) 车辆配送的单位运价:

客户i的送货时间窗:(Ei，Li) 车辆启用成本:cnh

车场个数:n(n=1，2，…，N) 车辆服务的顾客数:Cnh

车辆类型:h(h=1，2，…，H) 车辆载重:qnh，gi＜ qnh

车辆最大里程约束:Dnh路段i与j的平均速度:vij

每种类型的车辆数量:Knh中心车场的编号:0

客户i与j之间的距离:dij子车场编号:l+1，l+2，…，l+N

定义变量如下:

建立数学模型

目标函数:

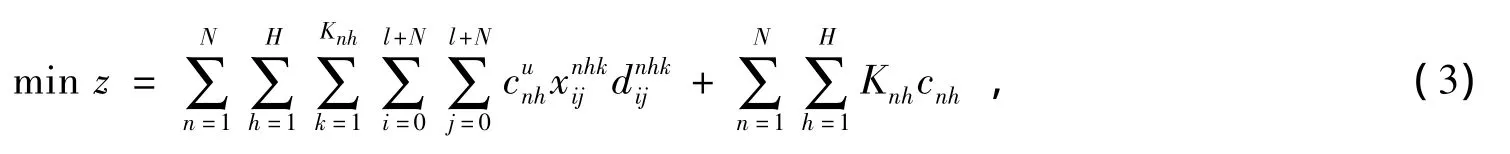
约束条件:

目标函数式 (3)表示总成本最小，包括运输成本及车辆启用成本。式 (4)和式 (5)表示每个客户只能由一辆车服务。式 (6)表示车场派出的车辆数不能超过该车场的车辆总数。式 (7)表示n车场h类型的车辆的行驶里程约束。式 (8)表示车辆从所在的车场出发，完成配送任务后，回到原车场。式 (9)表示每辆车所运送的货物重量不能超过此类型车辆的载重限制。式 (10)消除了车辆不是从车场出发的现象。式 (11)表示配送必须严格遵守客户的时间窗约束。式 (12)表示车辆服务的顾客数不小于1，则参与配送，否则没有参与。

2 算法设计

2.1 设计思想

扫描算法能初步对客户分组，从而缩短了寻优时间;而遗传算法的优点主要体现在以下几个方面:与问题领域无关切快速随机的搜索能力;搜索从群体出发，具有潜在的并行性，可以进行多个个体的同时比较;搜索使用评价函数启发，过程简单;使用概率机制进行迭代，具有随机性;具有可扩展性，容易与其他算法结合。但也有易早熟的缺点，采用模拟退火机制可以弥补这一缺点，模拟退火机制具有能往目标值较差处移动的机会，这种随机过程产生的机会使得该算法有能力避免陷入局部优化，而得到全局最优解。

2.2 扫描算法

扫描算法［13］(Scanning Algorithm)是Gillett和Miller在1974年提出的，即:旋转一个以车场为中心的射线对客户进行分区，直到不满足约束条件 (货运能力以及时间窗等)，然后开启新一次的扫描，直到平面上所有客户都被扫描了。

步骤1 按照就近原则对客户群进行分组，将客户安排给附近的快递公司所配备的车场。

步骤2 连接车场—客户，以车场0作为极坐标的原点，并以连通图中的任意一客户和车场的连线定义为角度0，然后对所有客户的位置进行坐标系的变换，全部转换为极坐标系;

步骤3 从最小角度的客户开始，建立一个组，按逆时针方向，将客户逐渐加入到组中，直到客户的加入违背了约束条件，然后建立一个新组，继续按逆时针方向将客户加入到组中;

步骤4 重复步骤2，直到完成所有客户的分组;

步骤5 对各个分组内的客户群，应用HGA求解单独的VRP。

2.3 混合遗传算法

2.3.1 产生初始种群及编码

采用文献 ［14］的方法，染色体表示为基因序列 (G1，G2，…，Gm)，Gi由三部分构成，车场编号DepotNum、车辆编号VehicleNum和排序值SortValue，表示客户i由n车场h类型的车辆服务，根据车辆所有客户的SortValue决定客户在路径中的位置。DepotNum、VehicleNum和SortValue随着初始群体的产生而生成。

2.3.2 适应度值计算

计算相应的目标函数值以及适应度函数值fj，j=1，2，…，m。用当前群体中最佳染色体的目标函数值z与当前染色体的目标函数值zi的比值作为适应度值，如式 (13)所示。

2.3.3 精英选择策略

精英选择［15］是群体收敛到优化问题最优解的一种基本保障。如果下一代群体的最佳个体适应值小于当前群体最佳个体的适应值，则将当前群体最佳个体或者适应值大于下一代最佳个体适应值的多个个体直接复制到下一代，随机替代或替代最差的下一代群体中的相应数据的个体。对于给定的t代规模为n的群体P(t)={a1(t)，a2(t)，…，an(t)}，一般描述为

fmax(t)=max{f(a1(t))，f(a2(t))，…，f(an(t))}，

fmax(t+1)=max{f(a1(t+1))，f(a2(t+1))，…，f(an(t+1))}．

if fmax(t)＞fmax(t+1)

replace randomly {aq(t+1)∈ P(t+1)}with{a'm(t)} (q=1，orq=1，2，…，M)

or replace the worst ones of{aq(t+1)∈P(t+1)}with{a'm(t)}

end if

2.3.4 自适应交叉

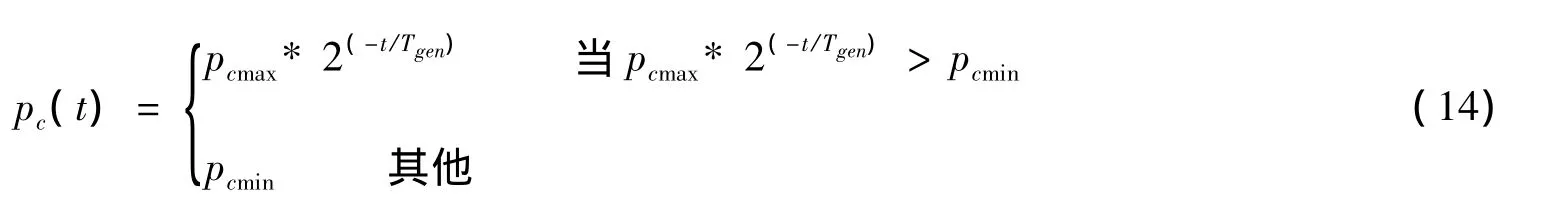
交叉算子［16］主要用于产生新个体，实现算法的全局搜索能力。考虑到整个种群的变化趋势及每个个体的变异机会，本节设计了与进化代数相关而与个体适应度无关的交叉概率计算公式，如式 (14)所示。t为当前进化代数，Tgen为预设的最大进化代数，pcmax为预设最大概率，pcmin为预设最小概率，pc(t)为当前种群的交叉概率。本文采取均匀交叉的方式进行交叉操作。假设两个父代为A和B，均匀操作如下:

1)随机产生一个与个体编码串长度等长的染色体C，C=c1c2…ci…cl，l为染色体编码长度。

2)若ci=0，A'在第i个基因座上的基因值继承A的基因值，B'在第i个基因座上的基因值继承B的基因值。

3)若ci=1，A'在第i个基因座上的基因值继承B的基因值，B'在第i个基因座上的基因值继承A的基因值。

2.3.5 混沌变异

采用混沌变异策略［17］，混沌变异形式如式 (15)所示。K(0，1)为 (－2，2)按混沌规律变化的序列。根据Logistic映射［18］，如式 (16)所示。式中，u表示种群序号，u=0，1，…，n;β表示混沌变量，0≤β≤1;μ表示吸引子，当μ取0～4时，Logistic映射为 ［0，1］间的不可逆映射，μ=4时，完全处于混沌的状态，此时产生的混沌变量β(u)具有很好的遍历性。β(u)经过放大和平移可得K(0，1)。变异算子的变化尺度对算法的性能有一定的影响。既要达到精度，又要搜索到全局最优解，所以在进化初期应采用逐渐缩小的变异尺度，利用文献 ［17］提出的变异策略，如式 (17)所示。kc为当前代数，Gen为最大迭代次数，δ为当前群体中某个体的某分量的变异尺度，α，β，γ为控制尺度收缩参数。

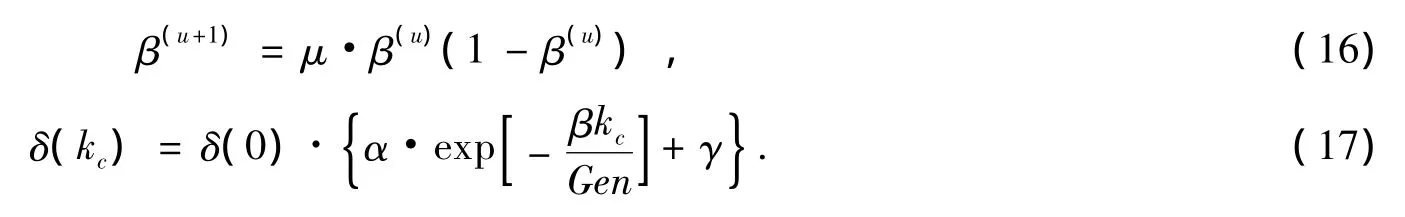
2.3.6 引入模拟退火机制

退火初始温度为T0，终止温度为Tend，温度冷却系数qcool。以fi为当前解，计算每一个个体的适应值fi'。若f'i＞fi，则以新个体替换旧个体;否则，以概率exp(fi－f'i)T接受新个体，舍弃旧个体。

2.3.7 终止条件

当算法运行达到最大迭代次数或者Ti＜Tend，算法终止。

2.4 3-opt局部搜索

采用3-opt局部搜索［18］方法，可以增强遗传算法的局部搜索能力。

步骤1从路径中删除3条边，并在路径的其他地方加上3条新的边，使路径保持完整。如果更换之后使路径长度变短，保留切换结果;否则，通过删除添加不同的边，并尝试其他更换方式。

步骤2重复步骤1，直到尝试了所有可能的更换方式，且不能再提高解的质量，则输出最优路径，退出算法。

3 仿真

3.1 实例

随机产生实例:某街道附近有4家快递公司为48个客户送货。客户的信息如表1所示，其中1～10表示A快递公司要送货的客户，11～20表示B快递公司要送货的客户，21～30表示C快递公司要送货的客户，31～48表示D快递公司要送货的客户。各公司都配备车场，如表2所示。最早发车时间为8:00，时速为60 km/h。Benchmark算例p03、p04和p06可从http://www.bernabe.dorronsoro.es/vrp/上获得。

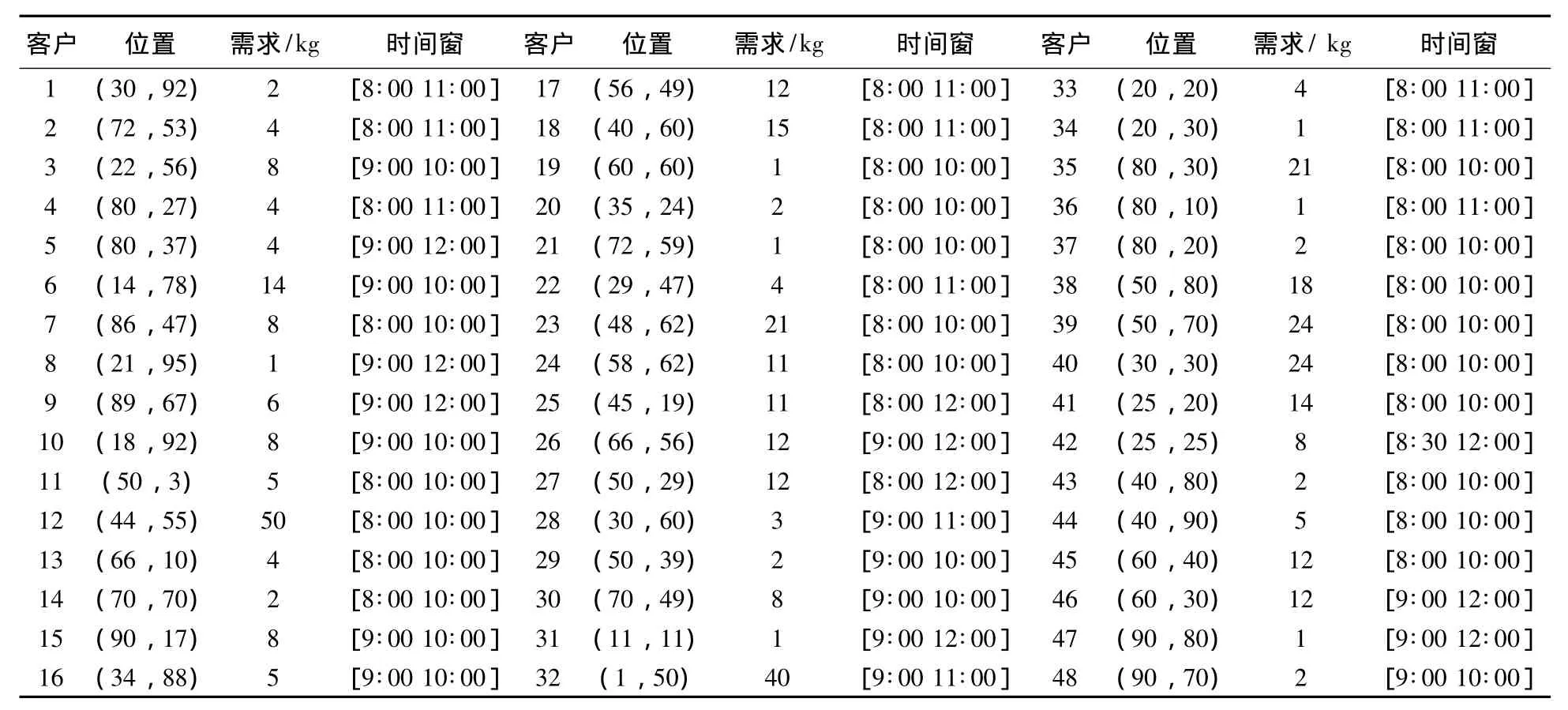
表1 客户信息

表2 车场信息

3.2 结果分析

实验是在Intel(R)CoreTMi5 CPU 2.6 GHz、内存为4.0 G、安装系统为win7的PC机上采用Matlab R2010b编程实现的。混合遗传算法参数设计:种群规模为sizepop=50，最大迭代次数TGen=300，pcmax=0.4，pcmin=0.004，变异概率pm=0.005，均匀交叉，单点变异，尺度收缩参数为α=1，β=10，γ=0.6，δ=0.6，T0=100，Tend=0，qcool=0.8。运行算法20次，取最好的结果。

针对快递公司协同配送问题，如果不考虑协同策略，就相当于多个车辆路径优化问题 (multiple vehicle routing problem，MVRP)。MVRP的最优行驶路线如图2所示，MDCVRP的最优行驶路线如图3所示。应用HGA对MVRP和MDCVRP两种模型求解的一次优化曲线如图4所示，HGA求解MVRP时，在第20代搜索到最优解，为320元;HGA求解MDCVRP时，在第15代搜索到最优解，为178元。可见，提出的MDCVRP模型相对于MVRP，约了44%的成本，所以该模型是优越的。并应用HGA、文献［4］中算法和文献［14］中算法求解MDCVRP的结果相比较，如图5所示，HGA在第15代搜索到最优解，178元;文献［4］中算法在第25代搜索到最优解，178元;文献 ［14］中算法在第34代搜索到次优解，188元。可见本文提出的算法在收敛速度和收敛质量两个方面都优于另外两种算法。两种模型中每辆车的行驶距离及车辆利用率如图6和图7所示，可见MVRP的总行驶距离远远大于MDCVRP，而车辆利用率却远远小于MDCVRP，进一步说明了提出的模型既能减少资源浪费又能节约成本。MDCVRP的最优行驶路线及行驶时刻表，如表3所示。由于车辆行驶里程约束和硬时间窗约束比较宽松，所以两种模型使用车辆数量一样，但是MVRP使用的车辆车型更大，成本更高，而且利用率不高，所以浪费了资源。如果以上两种约束更严格更紧致，可以预见MVRP使用车辆数量肯定多于MDCVRP。

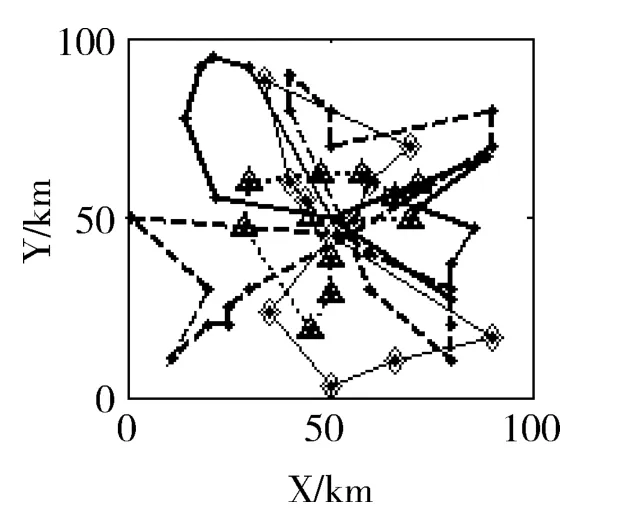
图2 MVRP的最优行驶网络

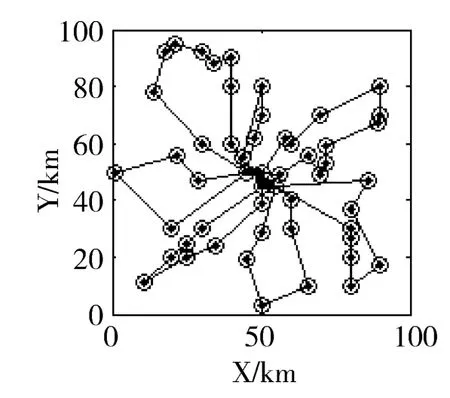
图3 MDCVRP的最优行驶网络

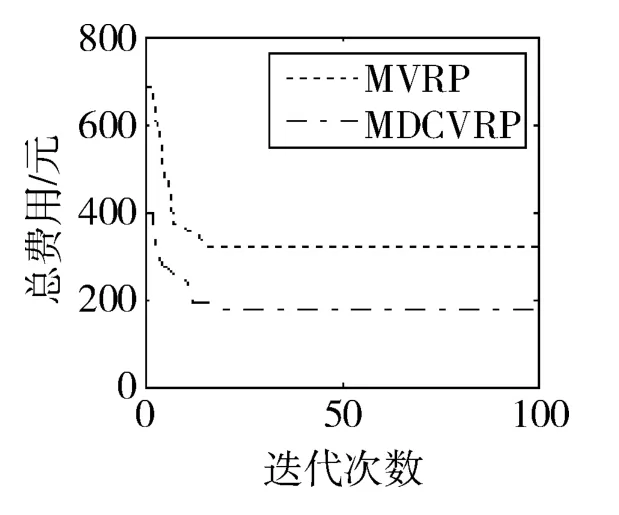
图4 HGA求解两种模型的一次最优进化曲线

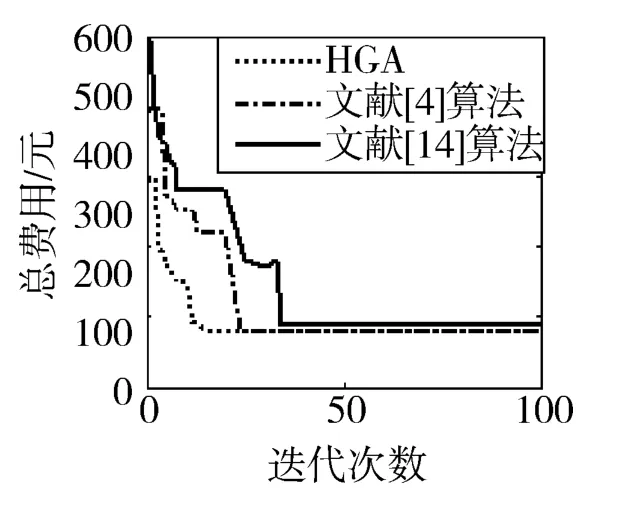
图5 三种算法求解MDCVRP的一次最优进化曲线

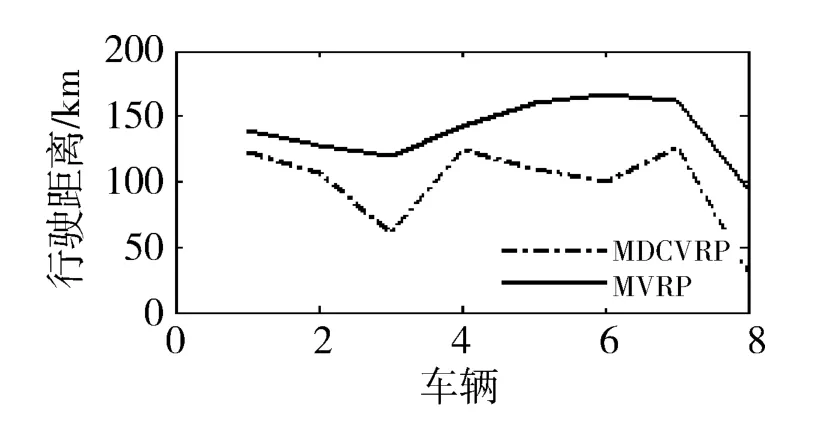
图6 每辆车的行驶距离 (MVRP和MDCVRP)

图7 每辆车的车辆利用率 (MVRP和MDCVRP)

表3 最优行驶路线及行驶时刻表

应用本文提出的HGA求解3个benchmark算例和文献 ［26］中的结果进行比较，对比结果如表4所示，从总运输距离、迭代时间、运行时间和偏差几个方面可以得出结论，虽然本文提出的算法得到的解与目前最好解还存在偏差，但是略优于文献 ［26］提出的算法。

表4 两种算法求解结果比较

4 结语

快递公司之间交付货物的过程是一个闭环VRP，首先通过最近车场距离方法将客户分配给不同的快递公司，将客户货物交付给离客户最近的快递公司即车场，求解快递公司之间的VRP，然后MDCVRP可转化为单车场多车型的路径优化问题，合理部署车辆资源，协同完成配送任务。应用基于精英选择策略、自适应交叉、混沌变异，并引入了模拟退火机制的HGA求解，最后应用3-opt局部搜索策略对解进行调整，得到最优解。本算法的优点在于:运用扫描算法对客户分组，简化了问题模型;考虑到收敛精度与进化代数的关系，混沌变异结合了“尺度收缩”思想，并采用了避免近亲繁殖的策略，引入模拟退火机制能有效克服传统遗传算法易早熟的现象;3-opt局部搜索对解的调整，从而提高算法的性能。下一步将要探讨的问题是考虑更为复杂的问题模型，如道路因素、客户需求紧急程度、个性化送货时间窗、1个客户可能在不同快递公司有多个订单、可分批配送、装卸货时间、分拣中转配送时间、周期性、开放式、客户随机性需求等，以及研究如何改进算法，使算法的性能更优。

［1］钟石泉，贺国光．多车场有时间窗的多车型车辆调度及其禁忌算法研究［J］．运筹学学报，2006，9(4):67－73．

［2］Mirabi M，Fatemi Ghomi S M T，Jolai F．Efficient stochastic hybrid heuristics for the multi-depot vehicle routing problem［J］．Robotics and Computer-Integrated Manufacturing，2010，26(6):564 －569．

［3］Yu B，Yang Z Z，Xie J X．A parallel improved ant colony optimization for multi-depot vehicle routing problem［J］．Journal of the Operational Research Society，2011，62(1):183－188．

［4］Kuo Y，Wang C C．A variable neighborhood search for the multi-depot vehicle routing problem with loading cost［J］．Expert Systems with Applications，2012，39(8):6949 －6954．

［5］Bettinelli A，Ceselli A，Righini G．A branch-and-cut-and-price algorithm for the multi-depot heterogeneous vehicle routing problem with time windows［J］．Transportation Research Part C:Emerging Technologies，2011，19(5):723 －740．

［6］Surekha P，Sumathi S．Solution To Multi-Depot Vehicle Routing Problem Using Genetic Algorithms［J］．World Applied Programming，2011，1(3):118－131．

［7］温惠英，孙博．基于离散粒子群算法的协同车辆路径问题［J］．公路交通科技，2011，28(1):153－158．

［8］温惠英，孙博．协同车辆路径问题的模糊规划模型和算法［J］．计算机应用研究，2011，28(2):442－444．

［9］张文静．协同粒子群算法及其在多车场路径优化问题中的应用［D］．上海:华东师范大学，2010．

［10］孙博．协同车辆路径问题模型及其算法研究［D］．广州:华南理工大学，2012．

［11］孙博，魏明，姚娟．基于车辆任务可靠性的协同车辆路径问题［J］．计算机应用研究，2013，30(8):2280－2282．

［12］刘冉．面向协同运输的车辆路径问题优化算法研究［D］．上海:上海交通大学，2011．

［13］黄海鹏．PSS模式下带时间窗多配送中心VRP建模及优化［D］．杭州:浙江工业大学，2010．

［14］汤雅连，蔡延光，赵学才．关联物流运输调度问题的改进遗传算法［J］．微型机与应用，2012，31(17):69－71．

［15］汪勇，杨海琴，张瑞军．基于强基因模式组织算法的VRPTW研究［J］．控制与决策，2011，26(4):606－610．

［16］汤雅连，蔡延光，郭帅，等．单车场关联物流运输调度问题的混沌遗传算法［J］．广东工业大学学报，2013，30(3):53－57．

［17］王华秋，曹长修．一种结合 O3-opt局部优化的智能蚂蚁算法研究［J］．计算机应用与软件，2010，27(010):89－91．

［18］Surekha P，Sumathi S．Solution To Multi-Depot Vehicle Routing Problem Using Genetic Algorithms［J］．World Applied Programming，2011，1(3):118－131．