基于Carathéodory-Fejér插值定理考虑误差界的负荷建模方法

唐秀明 袁荣湘 陈 君 彭小奇

（1.武汉大学电气工程学院 武汉 430072 2.中南大学信息科学与工程学院 长沙 410083 3.湖南科技大学信息与电气工程学院 湘潭 411201）

0 引言

负荷模型是电力系统安全稳定分析的基础，在某些情况下改变负荷模型甚至会改变系统稳定分析的定性结论[1]。负荷与系统中其他元件相比，构成成分复杂，包括大量性能各异的用电设备，且运行中存在着随机投切，这使得负荷建模难度很大，是电力系统领域公认的难题。因此，建立符合实际、考虑负荷随机特性的动态负荷模型具有十分重要的现实意义。

随着电力系统运行监测数据的丰富和系统辨识理论的发展，基于实测数据的负荷建模方法得到了专家学者的深入研究[2-5]。这些建模方法按模型的结构可以分为机理型[6,7]和非机理型[8-10]。机理型模型一般由静态部分和动态感应电动机两大部分构成，配电网络可单独考虑或间接在电动机模型参数中考虑。非机理模型包括常微分方程、传递函数、状态空间等形式的线性动态模型和非线性动态模型。

测量的负荷数据中的噪声会影响基于实测算法的模型参数的准确性。J.Yang 研究数据噪信比对辨识准确性的影响，当噪信比在0.2%～5%之间增加时，未进行噪声滤波时算法模型输出相对误差明显增加，进行滤波处理后算法模型输出误差值较小且增加幅度很小[11]。Y.G.Kim 使用离散小波算法对实测负荷扰动数据滤波，未说明滤波算法参数的适用性范围[12]；文献[13]将负荷数据中的噪声视为高斯白噪声，用低通滤波器滤除，但论文没有详细讨论滤波器的参数。这些考虑实测数据中噪声影响的文献，一般假设噪声为高斯白噪声，即均值和方差已知的概率分布。实际中负荷动态建模的实测数据数量有限，难以满足高斯白噪声的假设，且相应的分布参数也很难确定[14]。Milanese M 等提出将模型的未建模高阶部分及噪声假设为未知但有界的[15]（Unknown-But-Bounded，UBB）。系统中，UBB 噪声误差界限通常比统计特性更易获得，也更符合实际。

为了考虑实测数据中未知但有界的测量误差及随机扰动对负荷模型的影响，本文提出了基于Carathéodory-Fejér插值定理[16]（Carathéodory-Fejér Interpolation,CFI）的负荷建模方法。首先，将实测数据误差和负荷随机小幅扰动用未知但有界的非构造性误差在负荷模型输出端考虑对系统的影响；其次，根据哈代空间理论建立具有一定先验参数的负荷模型集，把先验参数和实测数据相容的条件转化为线性矩阵不等式求解，得到满足条件的解；最后，利用Nehari定理[17]和CFI定理构造出满足不等式考虑UBB误差的高阶线性传递函数模型。该负荷建模方法对一定误差界范围内的系统动态响应都能准确拟合，适用于基于实测数据的负荷建模。为检验本文负荷建模方法的有效性，论文从两方面对考虑误差界的CFI插值模型进行仿真，一方面用数值计算仿真，结果表明当数据中加入幅度为0.5%～10%的UBB随机干扰时，CFI插值算法模型输出的方均根误差值小于0.03，比最小二乘算法的方均根误差值小，模型的拟合效果较好，在UBB随机干扰误差界估计不准确时，该建模方法仍能得到较好的模型输出，当负荷构成比例改变时，在一定范围内，对模型参数的影响不大。另一方面，用大扰动时实测的数据进行负荷建模，考虑实际系统数据中的随机小干扰，模型仿真结果表明该CFI建模算法能准确拟合实际负荷动态特性。

1 哈代空间上的模型描述

哈代空间是单位圆盘上的解析函数空间，对于线性、时不变、因果及指数稳定的系统，可用哈代空间理论来分析。该理论广泛应用于系统辨识，控制系统分析等方面[18,19]。

假设线性时不变系统传递函数相对稳定裕度下界为ρ−1，系统在指数衰减的正弦信号激励下稳态增益上界为M，对于因果稳定系统，有ρ＞1，M＞0。令Dρ表示半径为ρ的圆面，即C为所有复数构成的空间。记Dρ的补集为，即。根据哈代空间理论，相对稳定裕度下界为ρ−1的线性时不变系统的稳定性等价于该系统的离散传递函数H(z)在上解析。由于不是闭 合有界的，难以直接使用最大模定理[20]和CFI 定理，因而引入变换z=λ−1，则系统H(z)稳定变换为H(λ)在闭合有界的Dρ上解析。在哈代空间中这类因果稳定的传递函数集合定义为

考虑图1所示线性时不变因果稳定系统模型，X为输入数据，；Y为输出数据，；N是数据长度；系统单位脉冲响应序列为，相应的传递函数为；系统的高阶未建 模部分、测量误差、负荷的随机小扰动等不确定的 UBB 随机干扰用输出端的有界干扰表示，是幅值小于ε的干扰集合，其中ε＞0；则考虑干扰的系统非伪模型集为p(y)

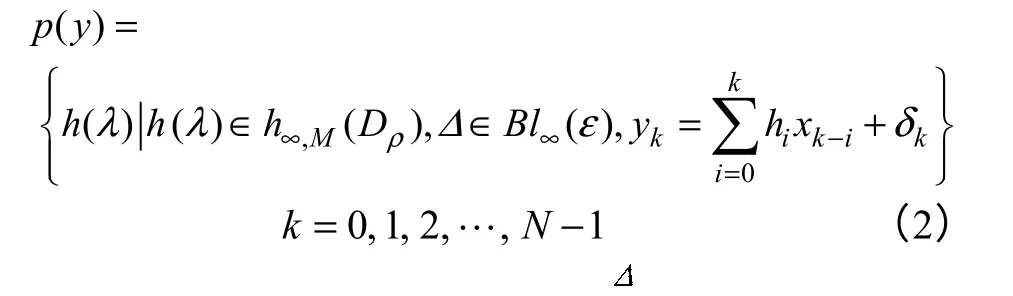
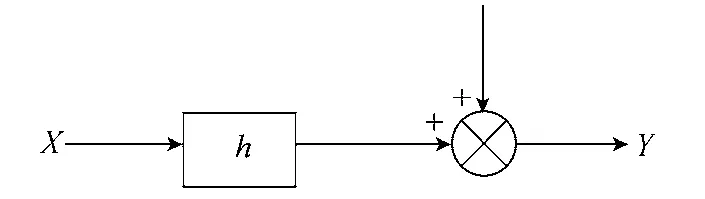
图1 考虑UBB 干扰的系统模型Fig.1 System model considering UBB disturbance

2 CFI 定理及在H∞,M(Dρ)函数空间的应用

2.1 CFI 定理

CFI 定理解决了给定范数约束条件下，在指定点函数取值为给定值的判断条件和函数的参数化方 法[21]。给定N维向量，定义矩阵函数定义的矩阵Λp

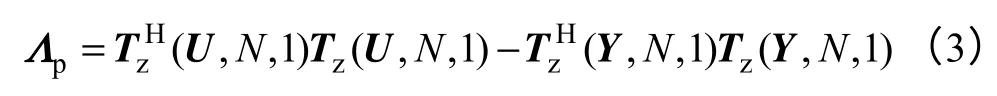
半正定时，存在矩阵函数F(λ)满足：①范数约束：F(λ)在是复平面上的单位圆面；②插值表达式F(λ)U(λ)=Y(λ)且F(λ)可由已知数据构造。

式（3）中，Tz(U,N,1)和Tz(Y,N,1)分别为由U=(u0u1…uN−1)和Y=(y0y1…yN−1)构成的下三角Toeplitz 阵

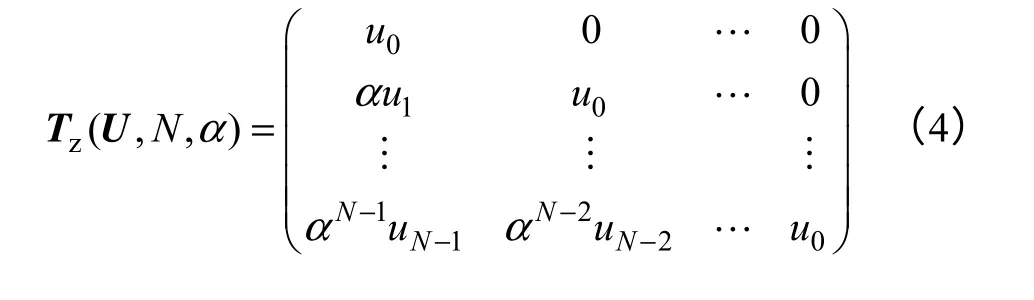
α=1时可简记为的转置，满足范数约束条件和插值条件的函数F(λ)为

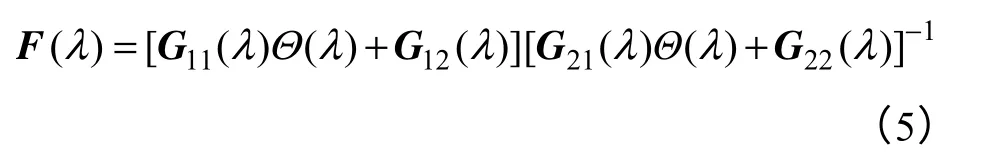
式中，Θ(λ)是在单位圆面D上解析且的 函数。矩阵函数F(λ)由已知矩阵Aπ、Aξ、B+、B−、C+、C−、S和Λp构造，矩阵之间需满足的条件[22]

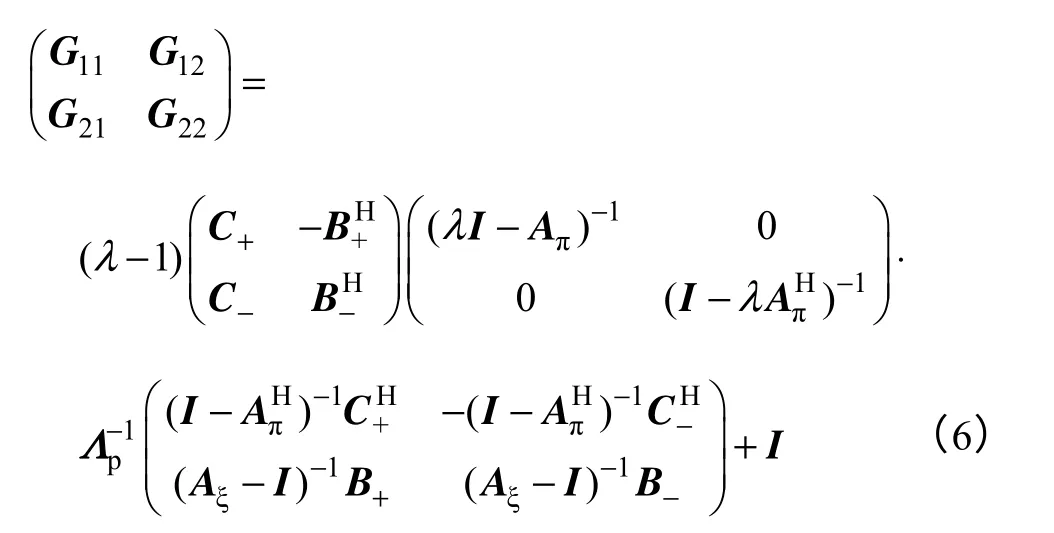
2.2 H∞,M(Dρ)函数空间CFI 定理的应用

由2.1 节内容知矩阵函数F(λ) ∈H∞,1(D1)，本文研究的对象电力负荷的传递函数属于H∞,M(Dρ)函数空间，需得到当插值函数R(λ) ∈H∞,M(Dρ)时 CFI定理在H∞,M(Dρ)上需满足的约束条件和插值函数。

引入变换λ→ρλ，利用CFI 定理可以证明[23]，当测量数据U、Y满足Ωp≥ 0时，存在传递函数R(λ) ∈H∞,M(Dρ)与测量数据相容。Ωp定义为

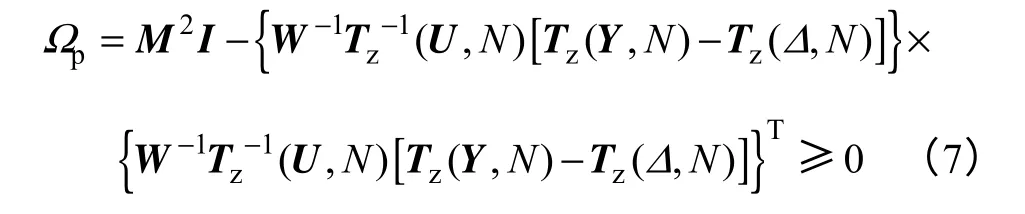
式中，W为对角阵，。插值函数

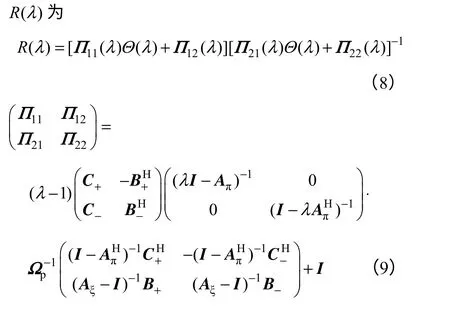
3 基于CFI 定理的负荷建模

3.1 UBB 噪声与模型的相容性

据CFI 定理，当负荷测量数据和模型UBB 误差界Δ满足式（7）的约束条件时，才存在插值函数R(λ)与已知相容。对矩阵X，当M2I−XXT≥0时，有，则式（7）的不等式约束条件转化为

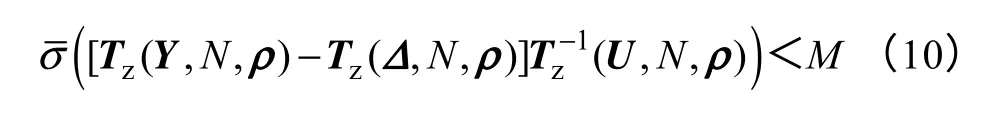
由Schur 补定理[24]，式（10）等价于线性矩阵不等式（Linear Matrix Inequality，LMI）

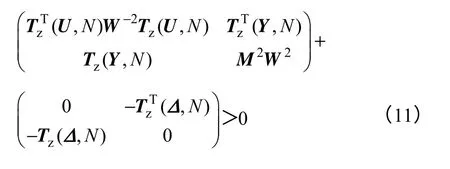
式（11）经过变换，可表达为关于决策向量Δ=(δ1,δ2,… ,δN)的LMI

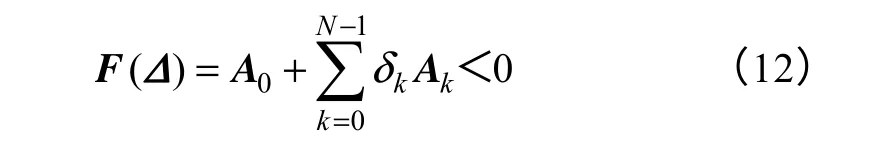
式中

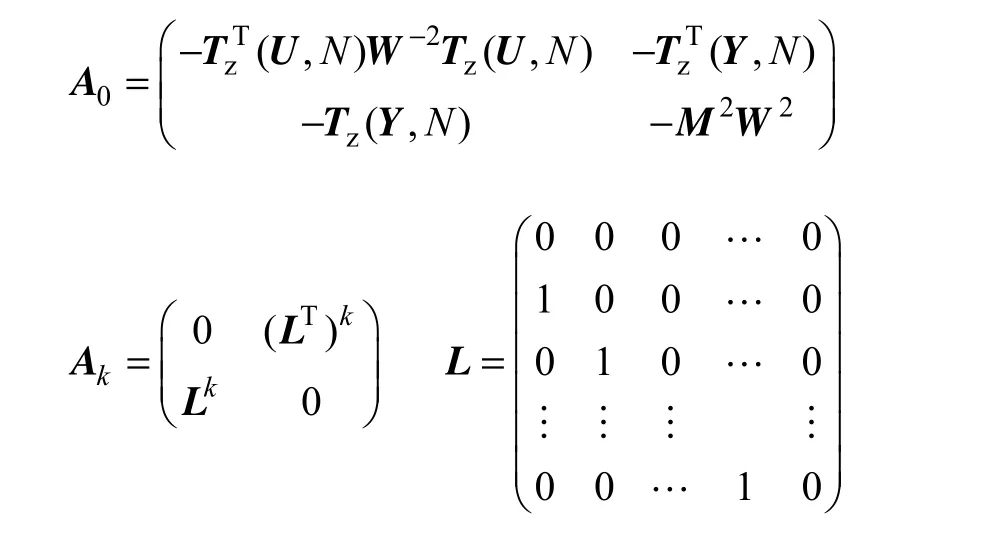
L是N N×维矩阵，决策向量Δ还需同时满足误差界 的不等式约束。此LMI 是关于特征 值最值的问题，即在一个线性矩阵不等式约束下，求矩阵的最大特征值的最小化问题。该问题的一般形式为

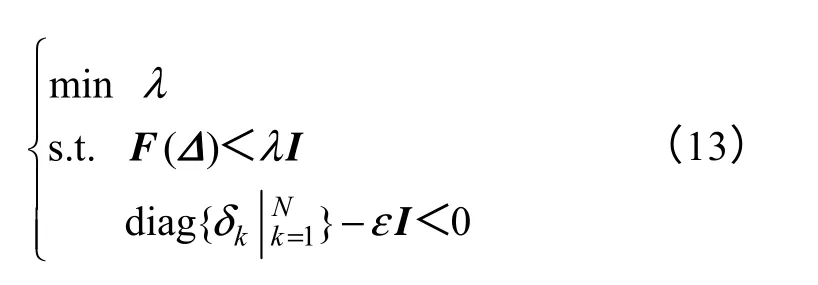
设解为Δ∗，若对应的λ∗＜0，则当扰动幅度在误差界内时，可以构造插值传递函数满足测量输入输出数据关系。将Δ∗构成的toeplitz 矩阵Tz(Δ∗,N,ρ)>代入Ωp中的Tz(Δ,N,ρ)，得到所求的系统传递函数hid

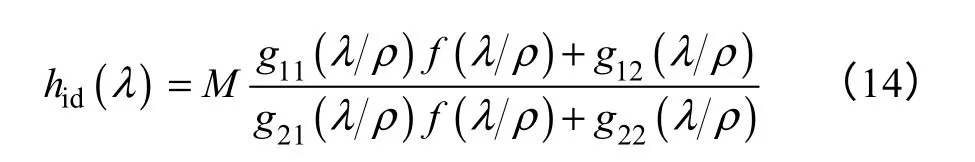
式中

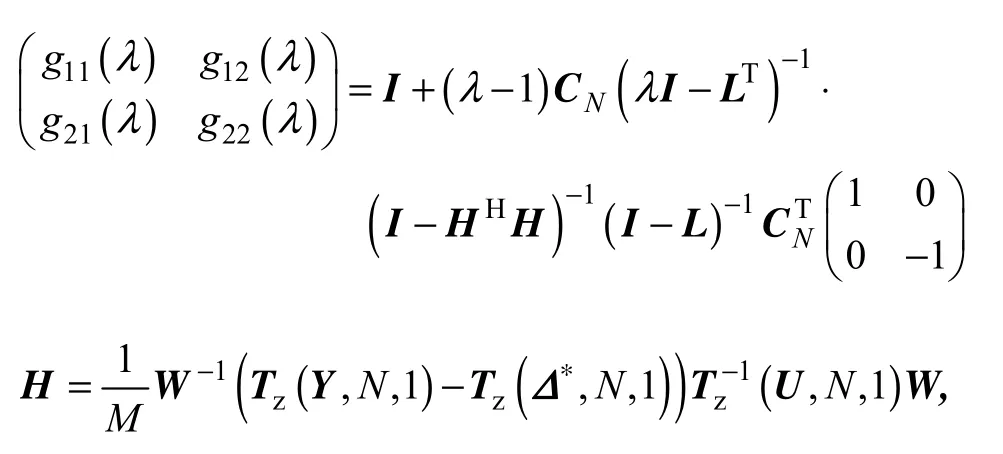
3.2 算法具体步骤

基于CFI 定理的算法具体步骤如下：

（2）若0λ∗≥ ，则先验信息与测量数据不相容，增大误差界值ε，转入步骤（1）（当0λ∗=时为临界情况，满足条件的传递函数唯一，也认为需增大误差界值）；若0λ∗＜ ，先验信息与测量数据相容，转入步骤（3）。

（3）根据∗Δ，构造矩阵H和NC及函数，得到被辨识系统的名义模型

4 仿真分析

4.1 不同幅度UBB 干扰下CFI 建模方法的输出

为了更全面方便地验证考虑未知但有界干扰的CFI建模方法，此处采用系统参数辨识研究常用的办法，即用精确模型（Accurate Model，AM）计算值代替实时采样值，通过对AM计算值加入不同幅度的随机干扰来研究CFI算法在UBB干扰下的鲁棒性。

AM由40%的静态ZIP负荷（其中恒阻抗负荷比例为30%，恒电流负荷为30%，恒功率负荷为40%）加60%的考虑机电暂态的一阶感应电动机负荷构成，感应电动机参数采用国内常用的典型参数[25]。系统电压故障扰动用ae−btcos(ct+d)+1函数模拟产 生，通过改变常数a、b、c、d的值可以模拟不同程度的故障扰动后电压下跌并恢复的过程。由AM模型可以得到故障期间的电压值及有功、无功响应。

为了探讨CFI算法对数据中的UBB干扰的鲁棒性，分别对AM数据加入干扰幅度为1%、5%、8%和10%的随机干扰，用加入有界干扰的数据模拟实测负荷数据。定义方均根误差（Root Mean Square Error，RMSE）[25]

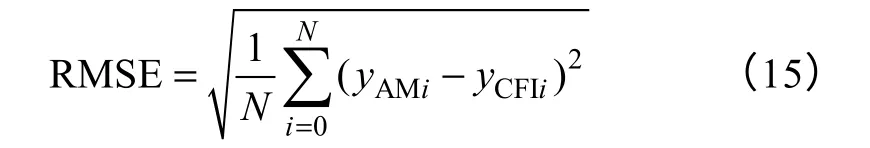
式中，N为采样数；yAMi为AM模型的第i个采样点数据；yCFIi为CFI算法模型第i个输出数据。其中CFI建模过程中使用的是加入有界随机干扰的数据。当RMSE接近0说明算法模型的输出与真实模型输出拟合程度高，反之RMSE越大说明拟合程度越低。

图2为UBB 干扰幅度为5%时CFI 建模算法有功及无功输出。从图2可以看出，数据中有干扰时，本文的模型输出响应曲线较光滑，不随误差界范围内上下扰动的数据波动，且对超出误差界范围的大幅变化的故障动态过程拟合程度高。

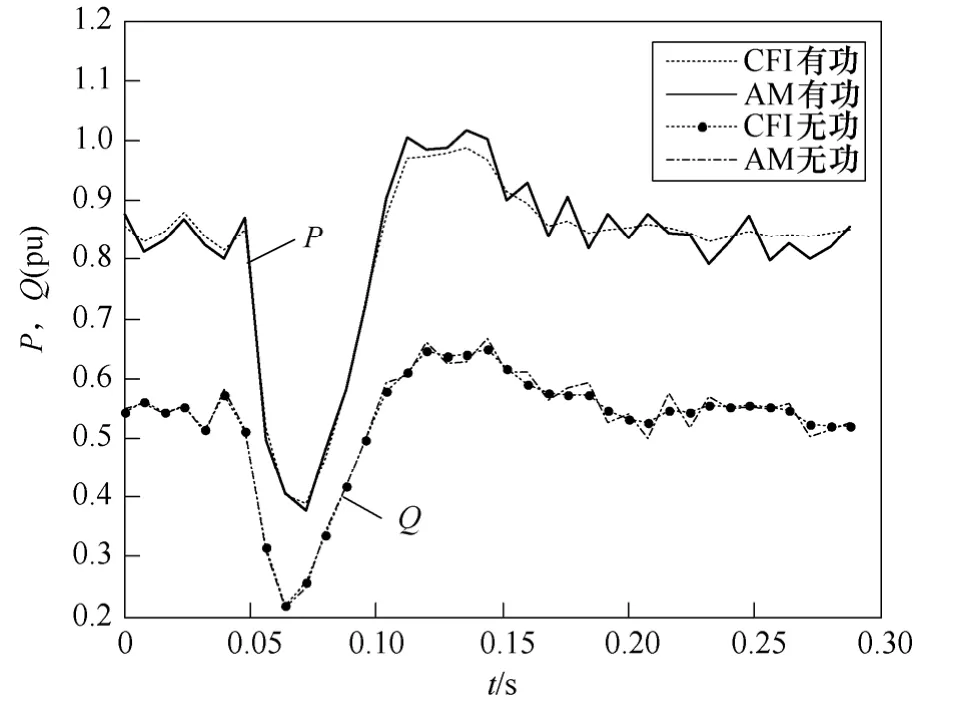
图2 UBB 干扰幅度为5%时CFI 算法和AM 算法输出Fig.2 Output of CFI and AM with 5% UBB noise

表1 为不同幅度UBB 干扰下，CFI 建模算法根据干扰数据所建模型输出与AM 无干扰真实模型输出的方均根误差值统计情况，同一干扰幅度进行20次仿真计算方均根误差值，表中为20 次方均根误差的平均值。由表中统计可知，当数据中有随机干扰时，本建模方法模型输出的方均根误差值较小，拟合度较高；干扰幅度增加，方均根误差均值增加，但当随机干扰幅度达到10%时，方均根误差均值仍能维持在3%以内，说明该CFI 建模方法的模型拟合准确度较高。

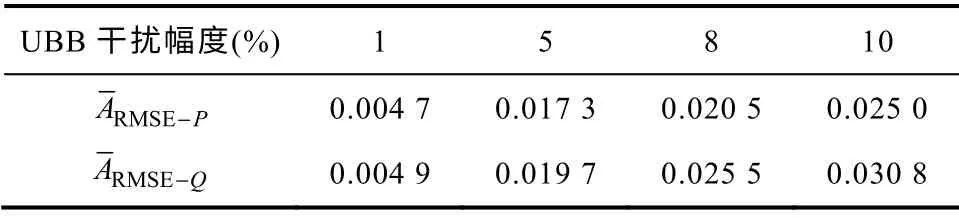
表1 不同幅度UBB 干扰下模型输出的方均根误差均值Tab.1 Mean of RMSE under different UBB noise

4.2 CFI 算法对噪声界的鲁棒性

负荷实测数据包含了测量设备准确度造成的误差和负荷的随机投切引起的波动，由于这些干扰精确的误差界值是未知的，即 CFI 算法中设定的UBB 误差界ε值可能大于或小于实际的干扰误差幅度。本文就CFI 算法中误差界值ε大小与实际干扰误差幅度的不同大小关系进行了仿真分析。

表2 中，用AM 输出叠加幅度为5%的随机干扰模拟实际负荷的非构造性误差，分别对CFI 算法中误差界参数ε取不同值仿真计算。从表2 可知，当CFI 算法所取误差界ε值与实际干扰幅度相差不大时，本文建模算法的模型输出方均根误差值小，模型拟合度高；图3是表2 中的不同误差界设定值下仿真的输出曲线，可以直观地看出输出曲线差异较小。由此可知，即使对于测量数据中误差界的估计值不准确，本建模方法的模型也能较好拟合负荷的动态输出。

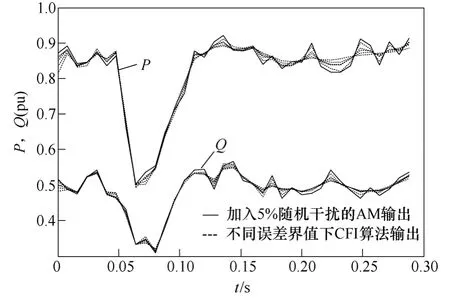
图3 不同误差界ε时CFI 算法和AM 算法输出Fig.3 Output of CFI and AM with difference error boundaryε

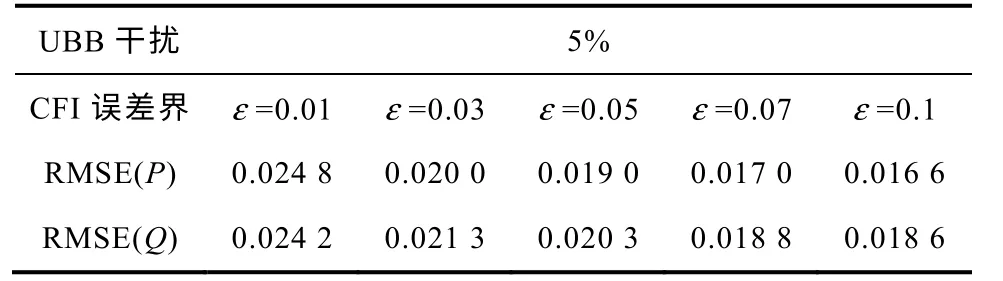
表2 不同ε值时CFI 算法模型输出方均根误差Tab.2 RMSE of CFI with different error boundaryε

4.3 随机干扰对CFI 与LMS 输出的影响比较

最小二乘法（Least Square Method，LSM）是应用广泛的辨识方法。对输入-输出系统，令u(kT)及y(kT)分别为系统的输入及输出采样值，简记为u(k)和y(k)，T为采样周期，则该系统可用差分方程描述为

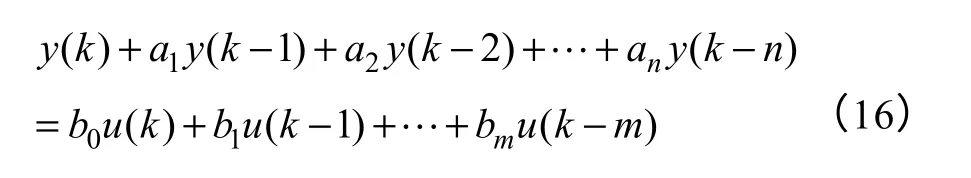
式中，aj、bj为待辨识的常系数；m、n为系统阶次。辨识准则为系统输出与测量值的方差最小。最小二乘法的差分方程模型与传递函数模型在本质上是相同的，其对应的传递函数形式为

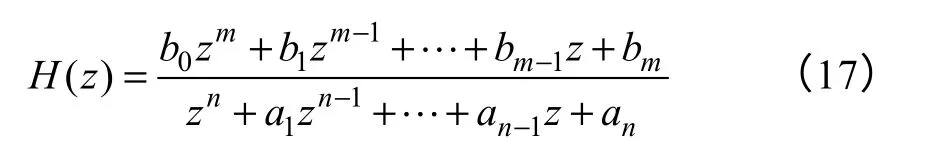
式中，aj、bj与差分方程中相同。因此选择LSM法与本文的方法比较，LSM的具体辨识方法见文献[26]。辨识使用相同的AM数据，加入不同幅度的UBB干扰，计算LMS及CFI两种不同方法的方均根误差，研究干扰对算法输出拟合的影响。

由表3中的数据可知，CFI模型输出的方均根误差与LSM算法相比小，即模型的输出拟合较好。随着随机干扰幅度的增加，最小二乘法的方均根误差值增大。这是因为只有当数据中的干扰为白色噪声时，LSM辨识方法的无偏性、有效性和一致性等优良性质才能得到保证，而有限的负荷数据中随机干扰难以满足高斯白噪声的统计规律。所以使用含有随机噪声的实测数据进行辨识时，LSM算法的输出误差受噪声影响明显。本文的CFI方法对干扰的假设仅为有界的，当扰动幅度在误差界内时被视为噪声。从表3的数据可知，本文算法对噪声的干扰有较强的鲁棒性。这说明在有限的数据下辨识时，本文对噪声的有界假设更符合实际也能够减少随机干扰对建模的影响。

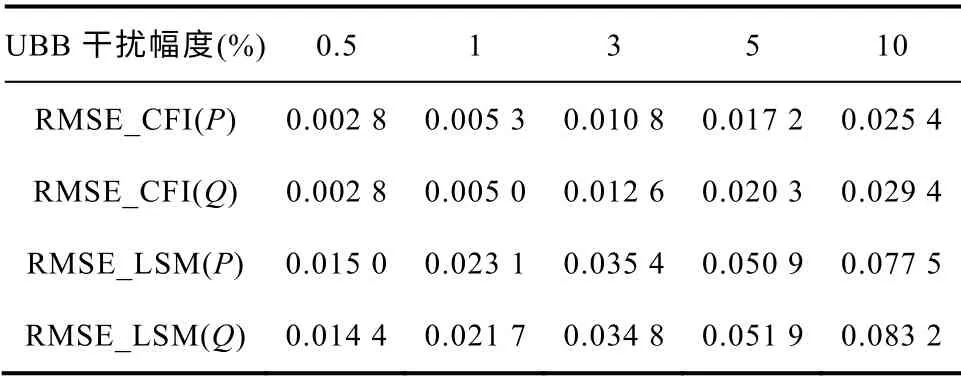
表3 不同幅度UBB 干扰CFI 和LSM 方法的 方均根误差Tab.3 RMSE comparison of CFI and LSM

4.4 负荷构成变化对模型的影响

电力负荷中各类用电设备的比例、容量大小等受时间、天气、运行方式等多种因素的影响。这些因素对负荷模型的影响主要体现在静态ZIP 负荷各部分构成比例的变化和动态感应电动机负荷所占比例的变化[27,28]。

为研究本文建模方法在考虑负荷时变性时的性能，本文考虑了不同静态ZIP负荷构成比例kz、ki、kp下CFI所建模型的差异及动态感应电动机负荷比例k_m改变时模型的变化。定义模型参数变化幅度，其中ia、ib分别是负荷构成变化前传递函数模型分母和分子的系数，具体见式（17），ia′、ib′分别是负荷构成变化后传递函数模型分母和分子的系数，maxαΔ、maxβΔ 表示系数变化的最大值。

修改精确模型中相应的参数，可得到负荷构成改变后的数据，以变化后的负荷数据进行建模，模型参数变化的情况见表4，参数的变化是与静态ZIP负荷占40%（其中恒阻抗负荷比例kz=30%，恒电流负荷比例ki=30%，恒功率负荷比例kp=40%），动态感应电动机负荷占60%时的模型参数比较。保持静态ZIP负荷比例不变，改变静态动态负荷比例值k_m，当比例值变化为10%时，模型参数变化的最大值为0.019 9；静态负荷构成改变时，假设静动态负荷比例k_m不变，保持一种静态负荷比例不变，其他两种负荷比例改变，从表中可以看出，当静态负荷构成比例改变为10%时，模型参数变化值最大为0.007 8。从参数的改变幅度可以看出，静态负荷成分变化对模型参数的影响较小，动态感应电动机负荷比例对模型的参数影响较大，但当负荷时变性等因素造成的负荷构成成分变化在5%内时，可以看出负荷变化对模型参数的影响可以忽略，这是因为本文的建模算法已经考虑负荷的随机干扰。当负荷比例变化达10%时，模型参数有变化，但本文CFI 建模方法得到的模型仍然能够较准确地描述负荷的动态响应。

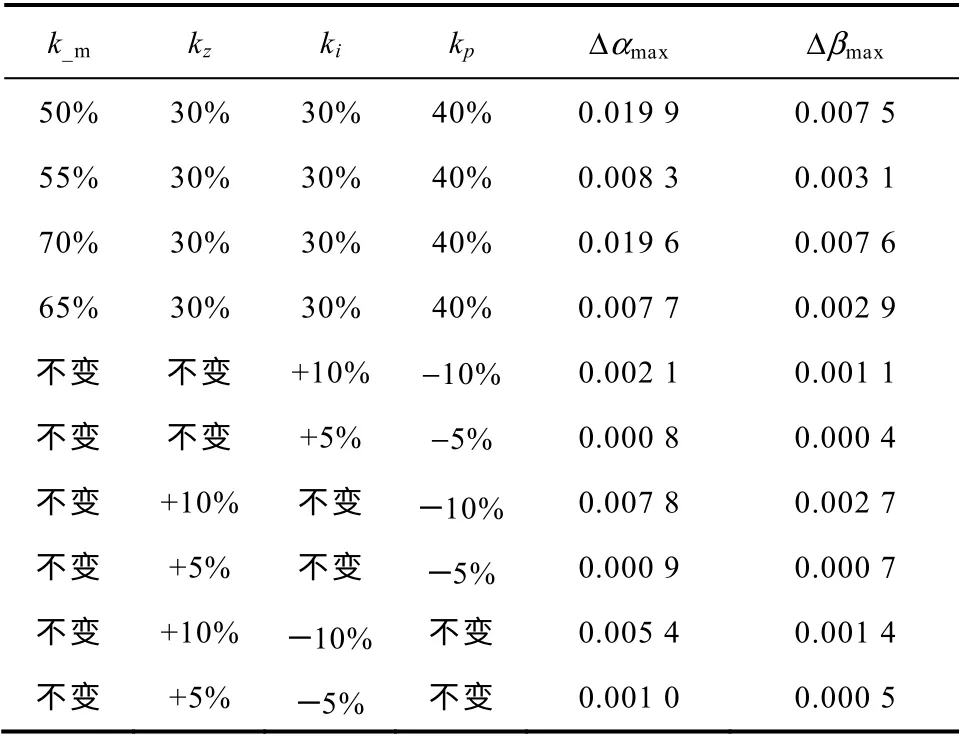
表4 负荷构成变化对模型参数的影响Tab.4 Effect on model parameters withdifferent load composition

4.5 电力系统实测数据的负荷建模

为进一步检验本文提出的CFI 辨识算法的实用性能，取某电网220kV 变电站大扰动实测的数据，经标幺化处理后用本文的方法进行负荷建模。考虑同步相量测量装置的测量准确度为0.5%[29,30]，正常运行时负荷的随机投切在短期内造成的有功及无功的波动幅度约为5%。CFI 方法对实测数据进行建模时的误差界取ε=5%。

模型有功及无功输出如图4和图5所示，可以看到本建模方法能较好地拟合实际负荷的动态响应。

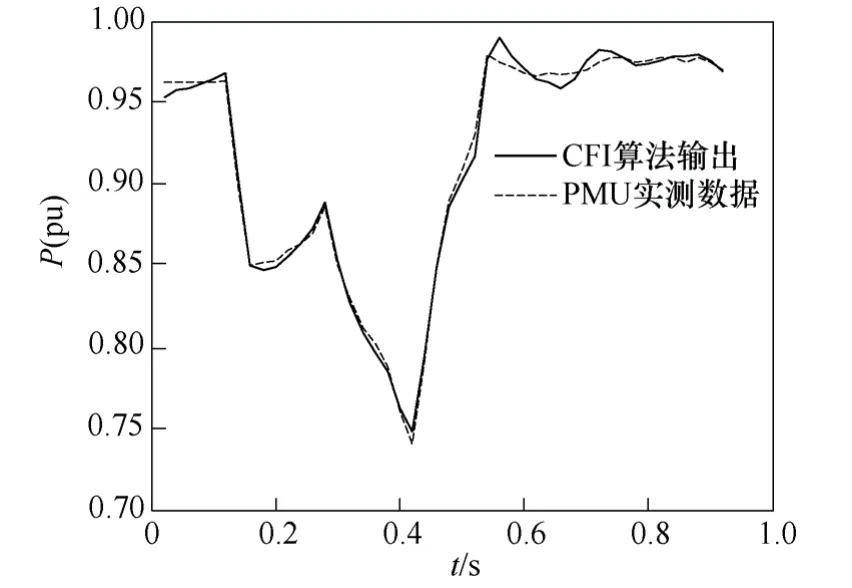
图4 实测及CFI 算法有功输出Fig.4 CFI and measured active power output

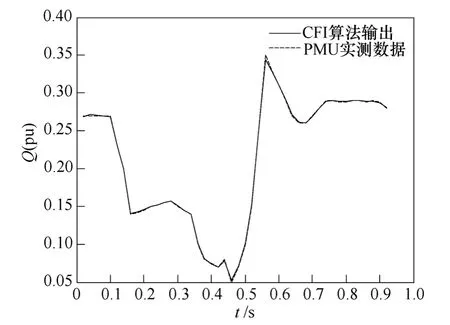
图5 实测及CFI 算法无功输出Fig.5 CFI and measured reactive power output

5 结论

针对电力负荷实测数据中存在随机小扰动及噪声的问题，考虑到实测数据量有限的情况，假设扰动及噪声是未知分布但有界的噪声。本文提出了考虑噪声误差界的CFI 插值算法。将模型和测量数据相容性问题用LMI 求解，得到在最不利情况下的解并据此构造负荷的高阶传递函数模型，当噪声幅度在误差界范围内，该模型能描述负荷的动态响应。仿真结果表明，实测负荷数据存在有界随机扰动时，CFI 算法对误差界估计值ε的准确性要求不高，算法的估计值在实际误差界值上下浮动时，该算法模型输出仍能较好拟合输出；和LSM 方法相比，CFI算法的输出方均根误差明显优于LSM 法，与噪声分布函数无关；当负荷构成比例在一定范围内发生改变，原建模模型仍能较准确地描述负荷的动态响应；采用变电站实测的数据进行建模的结果表明本算法具有实用性。

[1]Kosterev D N,Taylor C W,Mittelstadt W A.Model validation for the August 10,1996 WSCC system outage[J].IEEE Transactions on Power Systems,1999,14(3):967-979.

[2]Maitra A,Gaikwad A,Zhang P,et al.Using system disturbance measurement data to develop improved load models[C]//Power Systems Conference and Exposition,PSCE'06,2006:1978-1985.

[3]Kim B H,Kim H.Measurement-based estimation of the composite load model parameters[J].Journal of Electrical Engineering & Technology,2012,7(6):845-851.

[4]李欣然,钱军,王立德,等.配电网集结等效的异步电动机综合负荷模型及其总体测辨建模[J].电工技术学报,2009,24(4):175-185.

Li Xinran,Qian Jun,Wang Lide,et al.Synthesis induction motor model of power composite load considering distribution network structure[J].Trans- actions of China Electrotechnical Society,2009,24(4):175-185.

[5]韩冬,马进,贺仁睦.基于Bootstrap 的实测负荷模型参数优选[J].电工技术学报,2012,27(8):141-146.

Han Dong,Ma Jin,He Rengmu.Parameter optimiz- ation of measurement-based load model based on Bootstrap[J].Transactions of China Electrotechnical Society,2012,27(8):141-146.

[6]宋人杰,李文明.一种提高静态负荷模型参数辨识精度方法的研究[J].电力系统保护与控制,2013,41(6):89-92.

Song Renjie,Li Wenming.Research on improving the precision of static load model parameter identifi- cation[J].Power System Protection and Control,2013,41(6):89-92.

[7]黄玉龙,陈迅,刘明波,等.动态负荷模型参数辨识的微分进化算法[J].电工技术学报,2013,28(11):270-277.

Huang Yulong,Chen Xun,Liu Mingbo,et al.Differential evolution algorithm for dynamic load model parameter identification[J].Transactions of China Electrotechnical Society,2013,28(11):270-277.

[8]Visconti I F,Lima D A,Costa J,et al.Measurement- based load modeling using transfer functions for dynamic simulations[J].IEEE Transactions on Power Systems,2014,29(1):111-120.

[9]张红斌,汤涌,李柏青.差分方程负荷模型参数分散性的研究[J].中国电机工程学报,2006,26(18):1-5.

Zhang Hongbing,Tang Yong,Li Boqing.Study on dispersing of difference equation load model parameters[J].Proceedings of the CSEE,2006,26(18):1-5.

[10]肖锋,李欣然,王立德,等.基于神经网络的并行差分方程综合负荷模型[J].电力系统及其自动化学报,2009,21(1):41-47.

Xiao Feng,Li Xinran,Wang Lide,et al.Parallel difference equations load model based on neural network[J].Proceedings of the CSU-EPSA,2009,21(1):41-47.

[11]Yang J,Wu M,He Y,et al.Identification and application of nonlinear dynamic load models[J].Journal of Control Theory and Applications,2013,11(2):173-179.

[12]Kim Y G,Song H,Kim H R,et al.Particle swarm optimization based load model parameter identifi- cation[C].IEEE Power and Energy Society General Meeting,2010:1-6.

[13]Hain Y,Kulessky R,Nudelman G.Identification- based power unit model for load-frequency control purposes[J].IEEE Transactions on Power Systems,2000,15(4):1313-1321.

[14]熊传平,曹军杰,陈谦.基于小波分析的电力负荷模型辨识数据去噪[J].河海大学学报(自然科学版),2011,39(4):470-474.

Xiong Chuanpin,Cao Junjie,Chen Qian.A wavelet- based method for de-noising data of electric load modeling[J].Journal of Hohai University(Natural Sciences)2011,39(4):470-474.

[15]Milanese M,Belforte G.Estimation theory and uncertainty intervals evaluation in presence of unknown but bounded errors:linear families of models and estimators[J].IEEE Transactions on Automatic Control,1982,27(2):408-414.

[16]Rosenblum M,Rovnyak J.Hardy classes and operator theory[M].NewYork:Clarendon Press Oxford University Press,1997.

[17]Adamjan V M,Arov D Z,Kreĭn M G.Analytic properties of Schmidt pairs for a Hankel operator and the generalized Schur-Takagi problem[J].Sbornik:Mathematics,1971,15(1):31-73.

[18]丁思奇,曼苏乐,胡志勇,等.基于鲁棒H∞控制的静止同步补偿器研究[J].电力系统保护与控制,2012,40(13):98-103.

Ding Siqi,Man Sule,Hu Zhiyong,et al.Study of STATCOM based on robustH∞controller[J].Power System Protection and Control,2012,40(13):98-103.

[19]Ying S,Ge T,Ai J.H∞parameter identification andH2feedback control synthesizing for inflight aircraft icing[J].Journal of Shanghai Jiaotong University(Science),2013,18(3):317-325.

[20]周克敏,多伊尔,格洛弗,等.鲁棒与最优控制[M].北京:国防工业出版社,2002.

[21]Nikolov N,Pflug P,Thomas P J.Spectral Nevanlinna- Pick and Carathéodory-Fejér problems forn≤3[J].Indiana University Mathematics Journal,2011,60(3):883-893.

[22]Bolotnikov V.On the Carathéodory-Fejér interpolation problem for generalized Schur functions[J].Integral Equations and Operator Theory,2004,50(1):9-41.

[23]Chen J,Nett C N.The Carathéodory-Fejér problem andH∞identification:a time domain approach[C].Proceedings of the 32nd IEEE Conference on Decision and Control,1993:68-73.

[24]俞立.鲁棒控制:线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.

[25]王振树,李林川,牛丽.基于贝叶斯证据框架的支持向量机负荷建模[J].电工技术学报,2009,24(8):127-134.

Wang Zhenshu,Li Linchuan,Niu Li.Load modeling based on support vector machine based on Bayesian evidence framework[J].Transactions of China Electro- technical Society,2009,24(8):127-134.

[26]章健.电力系统负荷模型与辨识[M].北京:中国电力出版社,2007.

[27]李欣然,徐振华,宋军英,等.基于功率空间的分时段负荷模型参数在线修正[J].电工技术学报,2012,27(8):147-156.

Li Xinran,Xu Zhenhua,Song Junying,et al.On-line revising algorithm for load model parameters of substation in different daily periods based on the measured active power[J].Transactions of China Electrotechnical Society,2012,27(8):147-156.

[28]陈迁,徐箭,孙元章,等.考虑气温影响的负荷模型参数不确定性建模[J].电力自动化设备,2011,31(10):17-22.

Chen Qian,Xu Jian,Sun Yuanzhang,et al.Model of liad model parameter uncertainty considering temper- ature[J].Electric Power Automation Equipment,2011,31(10):17-22.

[29]王茂海,鲍捷,齐霞,等.相量测量装置（PMU）动态测量精度在线检验[J].电力系统保护与控制,2009,37(10):48-52.

Wang Maohai,Bao Jie,Qi Xia,et al.Online assess- ment of phasor measurement unit's performance based on sample data[J].Power System Protection and Control,2009,37(10):48-52.

[30]毕天姝,刘灏,杨奇逊.PMU 算法动态性能及其测试系统[J].电力系统自动化,2014,38(1):62-67.

Bi Tianshu,Liu Hao,Yang Qixun.Dynamic perfor- mance of PMU algorithm and its testing system[J].Automation of Electric Power Systems,2014,38(1):62-67.