间谐波环境下并联有源电力滤波器系统设计

张 超 马小平 张义君 任子晖

（1.山东科技大学电气与自动化工程学院 青岛 266590 2.中国矿业大学信电学院 徐州 221008 3.龙口矿业集团 龙口 265700）

0 引言

间谐波是指频率不等于基波频率（工频）整数倍的分量。随着高压直流输电装置、电弧炉和变频器等电力电子设备的应用，电网中出现大量的间谐波[1,2]。间谐波具有类似谐波的危害，而且会导致电压闪变和冲击性转矩[3]。由于间谐波的频率会随着谐波源设备运行状况而变化，导致其难以准确检测和消除。

有源滤波器（Active Power Filter，APF）已经在解决电网谐波污染问题方面得到广泛应用。在设计APF时，应考虑不同的电网环境和负载设备的要求，APF 应该可以在各种复杂电网环境下投入运行，并且运行时不会对电网产生干扰。目前，国内外关于间谐波的研究主要集中在检测方面，对间谐波的抑制方法，主要采用无源滤波器，利用APF 消除电网中间谐波含量的研究较少，并且现有应用于APF装置的谐波检测及控制方法并不能有效适用于间谐波环境下[4]。所以，在电网中间谐波含量明显时，研究APF 针对间谐波和谐波的共同检测及补偿方法具有重要意义。

目前谐波、间谐波的检测主要可以分为两大类：基于频域和时域检测方法。傅里叶变换是频域检测的经典算法，但由于间谐波的存在，傅里叶变换较难实现同步采样，采用非同步采样时，又存在着频谱泄漏等缺陷。采用加窗插值[5-7]、小波变换[8]、HHT（Hilbert-Huang transform）变换[9]的办法可以有效减少频谱泄漏等带来的误差，但存在实时性、边缘效应、频率分辨率低等问题。用现代谱估计的方法可以减少采样时间，提高频率分辨率，谱估计方法主要有：自回归（Auto Recursive，AR）谱估计[10]、三线性算法[11]、采用自适应、粒子群优化谱估计算法[12,13]等。

频域检测的方法可以获取谐波电流，但计算量较大，实时性较差。电网中电压、电流存在畸变时，传统功率理论已不适用，而现有时域检测方法主要基于各种非正弦功率理论，对APF 的适用性强，且算法本身构造简单，应用广泛。常用的基于功率理论时域检测方法，主要有两类：基于瞬时功率定义和基于Fryze 功率定义的方法。基于传统瞬时无功功率理论（p-q theory）的检测方法无法在三相电压不对称及发生波形畸变时，准确地检测出电网谐波电流；基于p-q-r 功率理论的检测方法增加了零功率的定义[14]，可以用于三相不平衡系统检测中；通用瞬时功率理论及其改进算法解决了在三相电压不对称及畸变系统中谐波和无功电流检测的问题[15,16]。FBD 法由Fryze 提出，经Buchholz 和Dpenbrock 完善，通过等效电导概念来分离电流，讨论各电流分量的物理含义，并且相比于传统瞬时功率定义的方法，不需要坐标变换，算法实现相对简单[17,18]；CPT（conservative power theory）定义了在三相不平衡及畸变系统中的瞬时功率[19]，与pq 功率理论、FBD功率理论相比，CPT 对不平衡及畸变系统中电流分解的表达更准确[20,21]，但对于电网含间谐波的情况需要进一步的研究。

重复控制（repetitive control）可以实现对周期参考信号的跟踪和周期干扰信号的抑制，与PI 控制、预测控制等相结合，可以实现对PWM 变换器取得较好的电流控制性能。但重复控制系统对非周期信号的控制以及非周期信号的干扰抑制性能较差，因此需要寻求改善重复控制系统非周期控制性能的方法。解决的思路有：高阶重复控制器（High- Order Repetitive Controller，HORC）[22]和自适应重复控制器[23]，这些方法在改善控制系统性能的同时，增加了系统复杂程度，使得系统稳定性难以实现。如果将非周期信号看作干扰，采用干扰观测器与重复控制结合的方法也是解决重复控制非周期控制问题的思路。等价输入干扰（Equivalent Input Disturbance，EID）方法[24]与通常干扰观测器不同，并不是基于系统逆理论，是一种主动扰动抑制方法。这种方法结构简单、易于实现，可以用于重复控制器中，提高重复控制系统的非周期扰动抑制性能。

本文以三电平SAPF 为研究对象，基于CPT 功率理论的定义，研究了间谐波环境下SAPF 指令谐波电流的检测，采用重复和PI 复合的控制方式对电网电流谐波以及间谐波分量进行补偿，通过引入EID 控制器，提高了SAPF 在非周期信号干扰下的控制性能，分析了所设计系统稳定性及灵敏度问题，给出了一种适合于间谐波环境下的SAPF 系统设计方法。仿真和实验表明，所设计系统可以准确检测电网谐波、间谐波含量，有效对电网谐波和间谐波进行补偿。

1 基于小信号干扰SAPF 数学模型

图1为二极管中点钳位式三电平变换器主电路拓扑，三电平变换器每相桥臂的四个开关可以组合出三种开关状态。

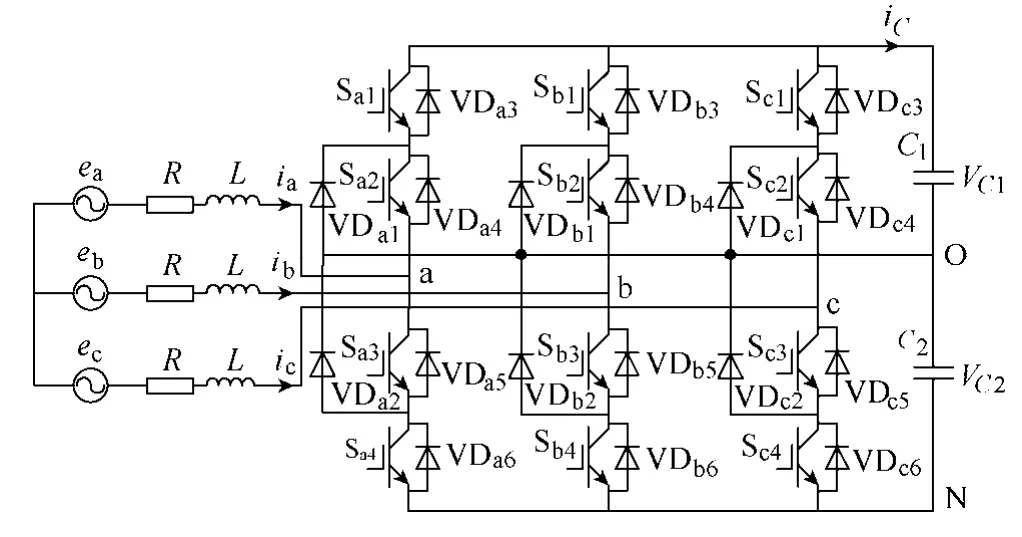
图1 三电平变换器结构拓扑Fig.1 The topology of three-level converter

根据基尔霍夫定律和图1所示结构，直接给出SAPF 在dq 旋转坐标系下状态空间表达式

式中

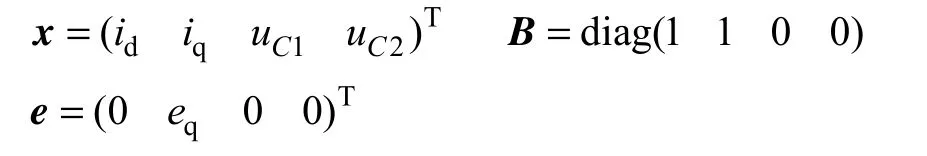
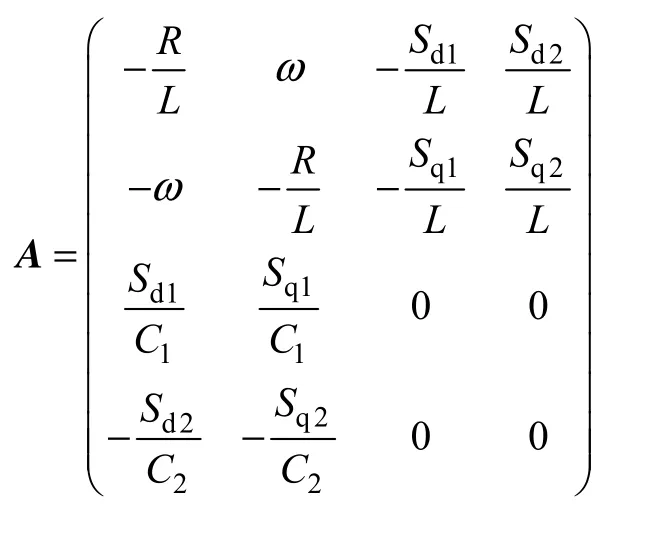
三电平SAPF 数学模型为非线性，可以在稳态值附近进行线性化，由扰动值引起稳态值附近的小信号变化可表示为

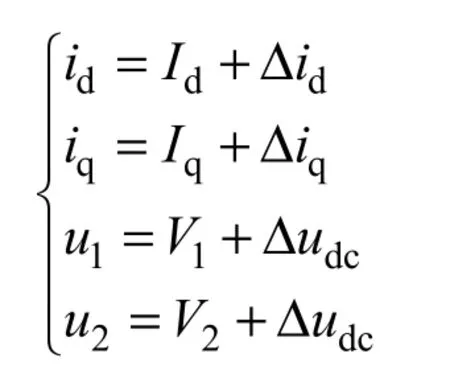
对SAPF 数学模型线性化并忽略高阶信号后，可以得到其小信号数学模型

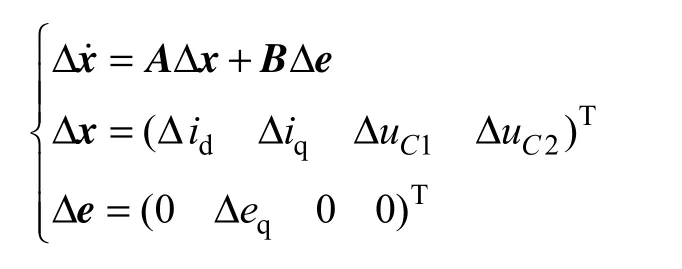
式中，下标d、q分别对应有功、无功分量。

2 间谐波环境下CPT 方法检测

2.1 CPT 定义

CPT 理论是近几年提出的关于非线性时域条件下的功率定义方法。对于一个连续变量x(t)，周期为T，定义原函数和导函数如下

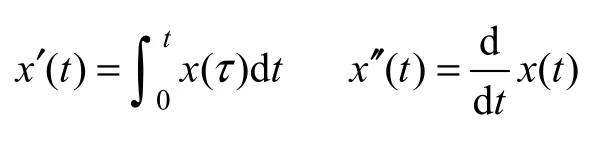
定义其直流分量

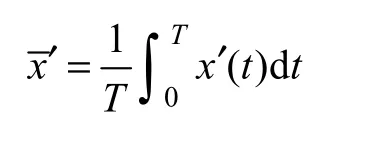
令ω=2π/T，定义x同源变量

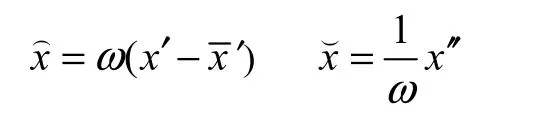
注意到x、和这三个变量在数量上是相等的，并且衡量单位相同，所以称这三个变量为同源变量。

根据CPT 理论定义，以三相系统为例，定义有功功率P

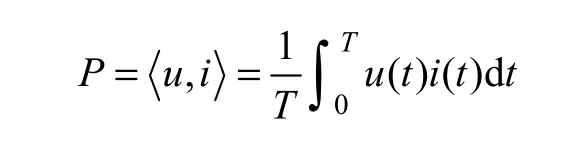
无功功率Q

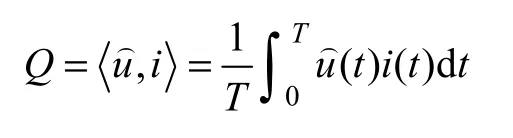
有功电流ia

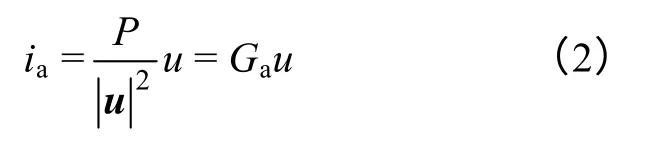
无功电流ir

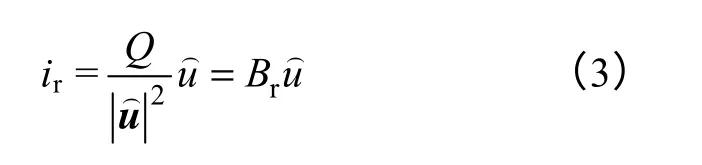
畸变电流iv

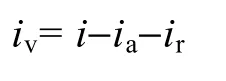
2.2 基于CPT 的间谐波检测方法

为了将CPT 功率理论应用于三相SAPF 谐波检测中，假设三相电源电压对称无畸变，初始相位角为0，标幺化处理后得

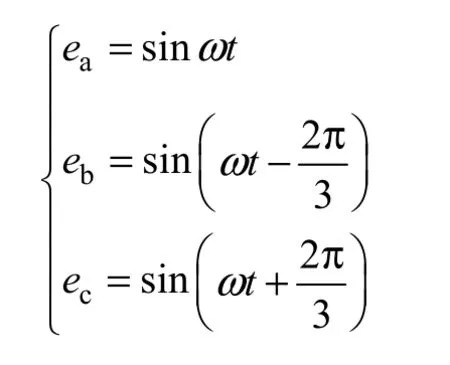
式中，ea、eb、ec分别为标幺化处理后的三相电源电压；ω为角频率。

对于ea来说，根据CPT 理论定义，其同源变量分别为

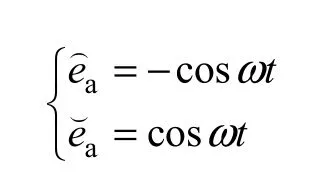
设三相负载电流为

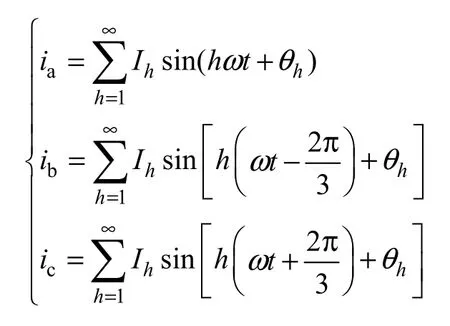
式中，ia、ib、ic分别为三相负载电流；I为谐波电流分量的幅值；θ为谐波电流分量的初始相位角，下标h为谐波次数，当h=1时，表示基波分量；当h取整数时，表示基波倍频分量；当h取非整数时，表示间谐波分量。

根据CPT 理论有功功率定义，代入电压、电流表达式，计算得

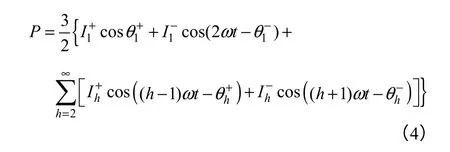
若将式（4）交流分量滤除，可得线性有功功率

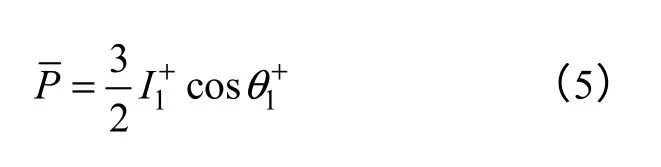
可以看出，式（5）与电流基波有功分量对应。根据CPT 理论，设三相电源电压的同源变量为

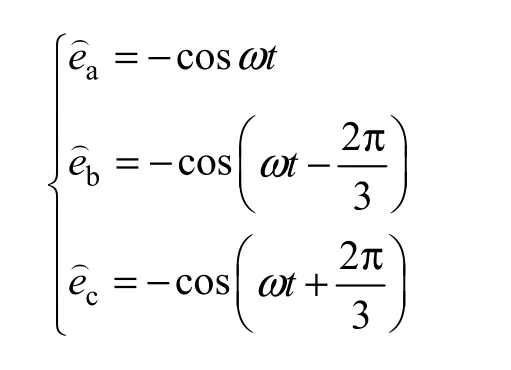
根据CPT 理论无功功率的定义，同样可以得到瞬时无功功率Q

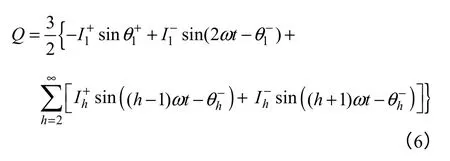
将式（6）交流分量滤除，可得线性无功功率

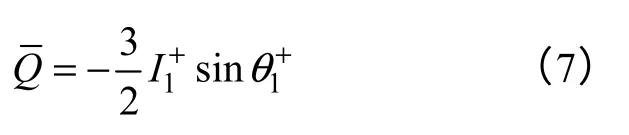
将式（5）和式（7）代入式（2）和式（3），两式相加即得基波正序分量，除基波正序分量外其余分量即为SAPF 的谐波检测信号。基于CPT 功率定义的SAPF 谐波检测系统如图2所示。

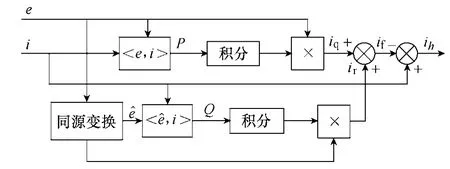
图2 基于CPT 谐波检测系统Fig.2 Harmonic detection system based on CPT

3 基于EID 重复控制补偿

3.1 控制系统设计

根据三电平APF 数学模型，按照等价输入干扰、重复控制的设计方法，设计APF 电流环补偿控制系统如图3a 所示。

APF 补偿信号是除去基波外的谐波信号，主要包含基波倍数频率次谐波。当电网间谐波含量明显时，补偿信号混入非基波倍频信号，重复控制器无法对这些非周期信号进行控制。复合重复控制系统由改进重复控制和PI 控制器并联而成。通过重复控制对周期信号控制，提高APF 补偿精度。PI 控制调节重复控制的延迟特性，并对非周期信号控制，改善APF 的动态特性。考虑采样等因素，PI 控制器加入一拍延迟环节。控制系统框图如图3b 所示。

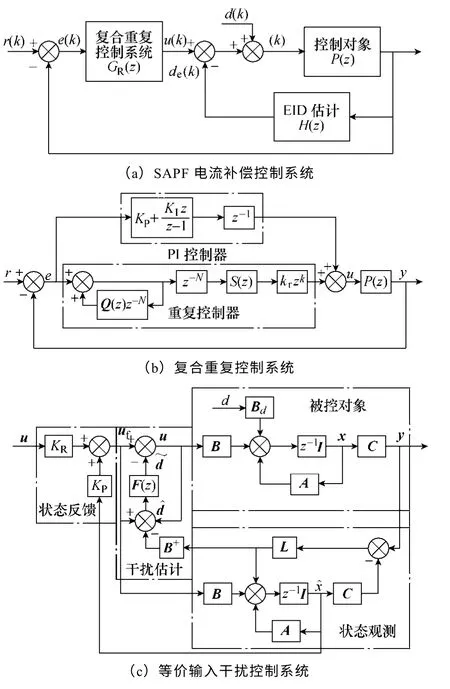
图3 SAPF 电流补偿控制系统Fig.3 The current compensation system of SAPF

随着APF 中器件老化，器件参数会有波动，再加上死区效应、负荷波动等因素影响，APF 在实际运行中会出现周期和非周期干扰。对于重复控制器来说，可以消除周期干扰影响，但对于非周期干扰，控制效果反而会恶化。本文引入等价输入干扰控制器对非周期信号干扰进行抑制，提高APF 电流补偿控制器的鲁棒性，改善APF 补偿效果。

根据等价输入干扰定理，对于如图3a 所示控制系统，由输入干扰d(t)引起的输出为y(t)，那么存在一个从控制输入引入的等价输入干扰de(t)，满足de(t)与干扰信号d(t)产生同样的输出。

EID 控制系统主要包括用于等价输入干扰的干扰估计器和用于状态反馈的状态观测器，图3c 中控制系统干扰de(t)可以用下式表示

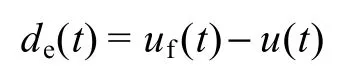
由图3c 可以得到等价输入干扰估计器所推测干扰表达式为

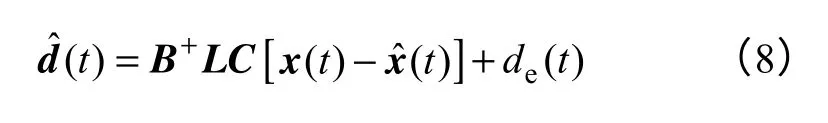
从式（8）可以看出，当状态观测器观测状态与被控对象一致时，等价输入干扰估计干扰值与实际一致。

3.2 控制系统灵敏度分析

灵敏度是反映控制系统性能的重要指标，对于图3a 所示控制系统，灵敏度定义为外部扰动d对控制对象输出y的传递函数，也可理解为外部输入信号r对误差信号e的传递函数。所以，灵敏度反映了控制系统对输入信号的跟踪特性，以及对扰动的抑制特性。图3a 所示控制系统灵敏度函数S为

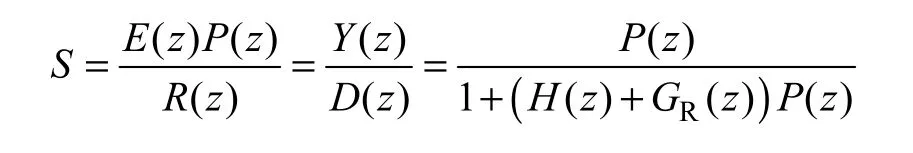
控制系统的设计，除了考虑数学模型和性能指标外，其设计还要受到一定约束。灵敏度函数是控制系统重要性能指标，但不是可以任意取值的，要受到Bode 积分定理的约束。根据Bode 积分定理，对数灵敏度的积分是一个常数，如果控制系统稳定，则积分为零，即

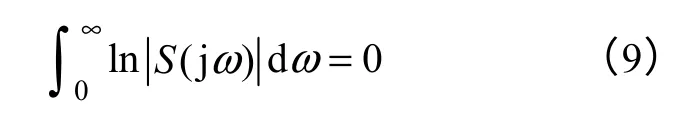
当S＜1时，对数灵敏度为负；当S＞1时，对数灵敏度为正。所以，根据式（9），积分为零即要求对数灵敏度正负面积相等。虽然控制系统性能要求灵敏度越小越好，但是根据Bode 积分定理，灵敏度在某一频段被调低后，必然会在其他频段升高。重复控制就是在周期信号频段将灵敏度降低，导致非周期频段灵敏度升高，造成非周期信号控制性能的恶化。

对于重复控制系统，其灵敏度函数Sr为

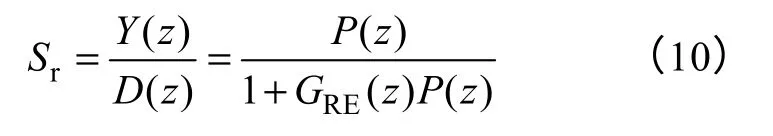
加入PI 控制后，系统灵敏度函数Sp为

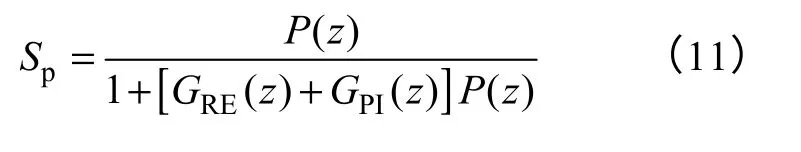
对于图3c 所示控制系统，其灵敏度函数Se为

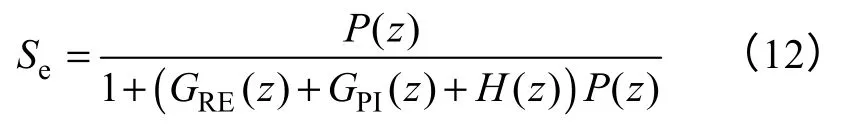
式中

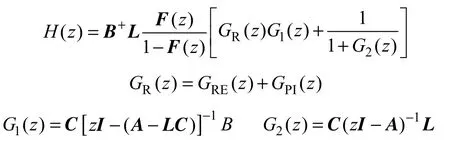
比较式（10）～式（12），可以看出，引入PI控制和EID 控制后，通过调节PI 与EID 控制传递函数，可以使得系统灵敏度函数减小。

图4为根据式（10）～式（12），针对SAPF控制系统设计重复控制、重复和PI 复合控制，以及加入EID 控制的三个控制系统灵敏度函数比较。可以看出重复控制在基波即50Hz 倍频处，灵敏度函数处于低点，而在基波倍频之间的非周期位置，灵敏度函数处于高点。所以，重复控制对于基波及倍频信号有很好的跟踪或抑制作用，而对于非周期信号，以SAPF 来说，主要是指间谐波及非周期干扰，控制性能则会恶化。

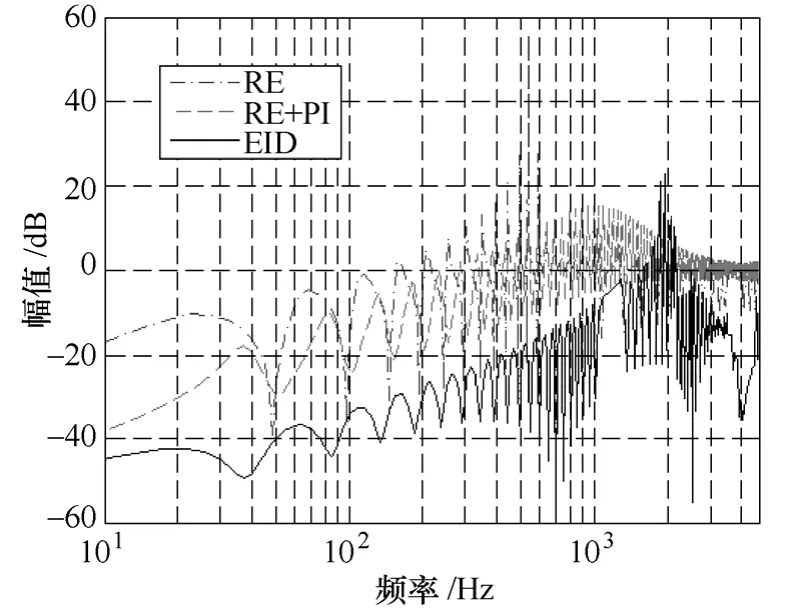
图4 控制系统灵敏度函数比较Fig.4 The sensitivity comparison of control system

从图4还可以看出，加入PI、EID 控制后，灵敏度函数低频段整体下拉，显示控制系统对于基波倍频信号以及非周期干扰信号的控制性能提升，符合式（9）体现的控制规律。同时，根据前述Bode积分定理以及图4所示，EID 的引入恶化了系统部分高频段的控制性能。SAPF 的作用主要在于抑制电网当中低频特征次谐波含量，虽然EID 控制的引入使得系统对于部分高频信号控制性能变差，但并不会对SAPF 在实际应用时的性能造成影响。

3.3 控制系统稳定性分析

系统稳定性是控制系统设计时的最基本要求。只有在控制系统稳定的前提下，才能进一步进行系统设计，考虑系统其他性能指标的要求。

对于图3a 所示控制系统，可以看成重复和PI的复合控制系统与EID 系统两个子系统串联而成。整个控制系统的稳定性，可以看成是两个子系统同时稳定，由于复合重复控制系统与EID 控制系统中的控制参数选取没有重合项，两个子系统可以单独设计。对于图3b 所示复合重复控制系统，令PI 控制器传递函数为GPI(z)，直接给出其特征方程为

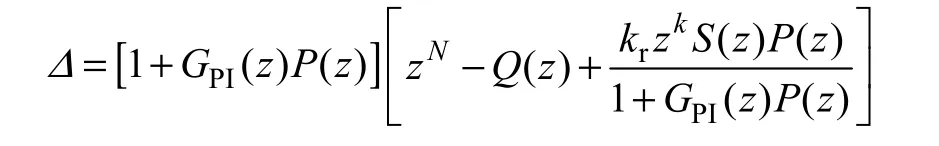
复合重复控制系统特征方程包含两个部分，不难看出1+GPI(z)P(z)为PI 单独控制时的特征方程，后一部分为加入重复控制后的特征方程。所以，复合重复控制系统的稳定，是在单独使用PI 控制系统稳定前提下，要求经PI 控制后的系统在重复控制下也是稳定的。

为了分析控制系统稳定性，令图3a 系统中输入信号及干扰为零，以干扰估计器中低通滤波器F(z)输入输出作为系统输入输出，可以将图3c 所示EID 控制系统等效为图5所示系统，图中虚线框部分G(z)为

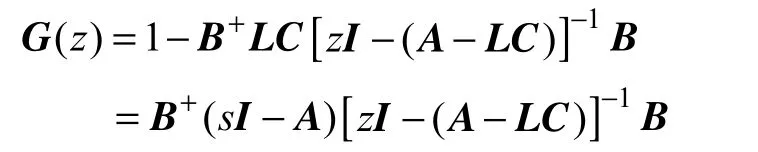
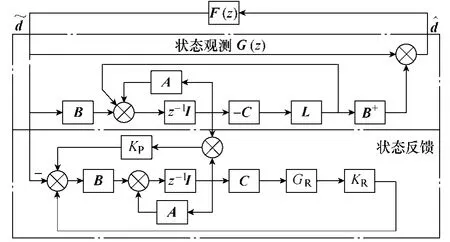
图5 EID 等效控制系统Fig.5 The equivalent control system of EID

由图5可以看出，EID 系统设计分为状态观测、低通滤波和状态反馈三个部分。状态反馈部分不会影响其他系统稳定性，可根据LMI 或最优控制等方法独立设计。对于状态观测和低通滤波系统，根据小增益定理，在状态观测与低通滤波系统分别稳定前提下，整个系统稳定还需满足系统传递函数的H∞范数小于1，即满足

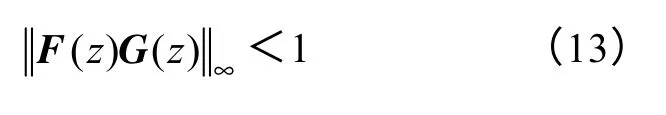
3.4 控制系统参数设计

控制器增益L的设计可以看作是输出反馈H∞问题。对于低通滤波器F(s)，设定输入和输出分别为ω(t)、z(t)。那么，系统状态空间表达式可以写成

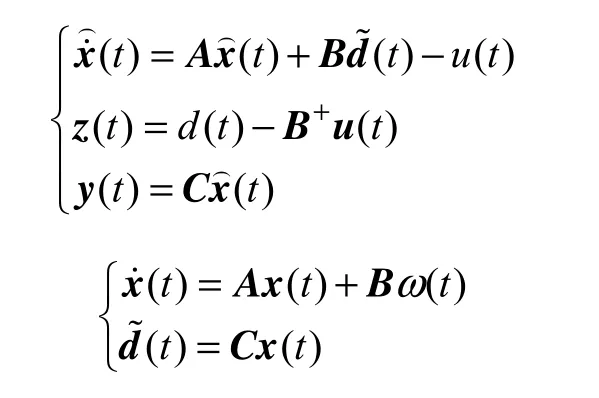
对于如图5所示控制系统，G和F系统可以写成如下形式

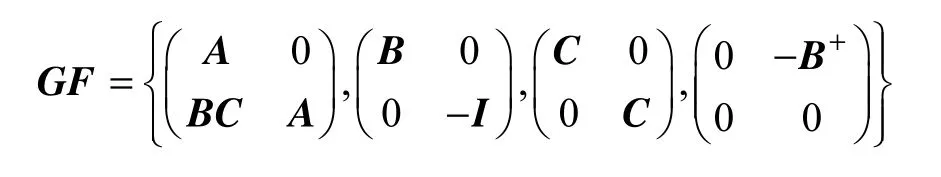
需要设计输出反馈控制器u=Ly来保证式成立，可以得到增益L满足

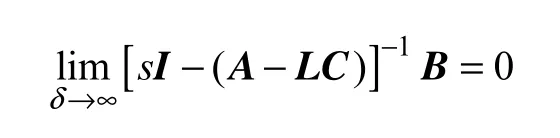
综上所述，控制系统设计步骤如下：

（1）设计系统反馈增益KP和KR。

（2）低通滤波器F(s)需要满足如下式子成立

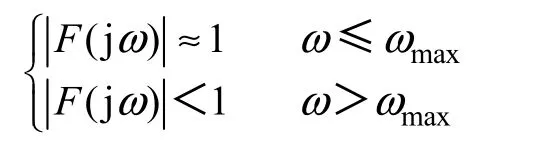
式中，ωmax为非周期干扰角频率的最大值。

（3）设计观测器增益L，保证G(s)系统稳定。

（4）调整控制器参数至系统满足控制要求为止。针对图3所示控制系统，根据最优控制设计方法，对系统反馈增益KR、KP进行设计。构建控制系统小信号数学模型为

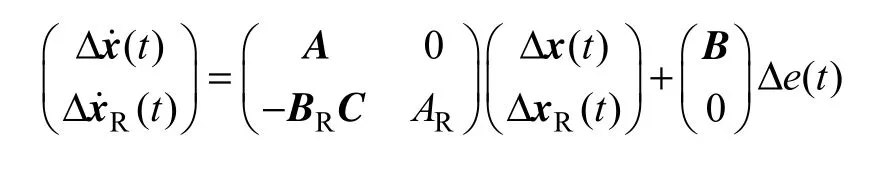
取线性二次型（Linear Quadratic,LQ）性能指标

得到

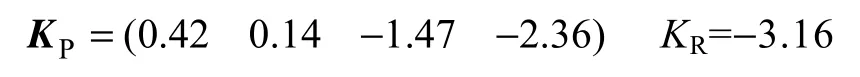
针对式（1）所示系统的对偶系统，有

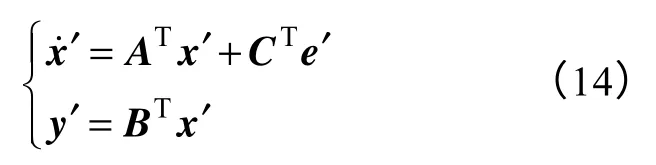
给出性能指标

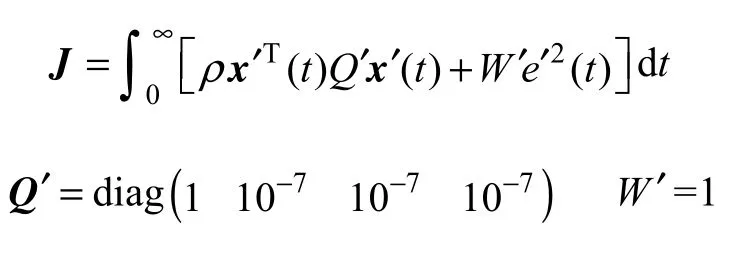
通过调整ρ的取值，使得式（13）成立，取ρ=107，得到

4 仿真和实验验证

为了验证所设计SAPF 控制性能，以Matlab 软件和三电平实验平台为依托，建立SAPF 控制系统仿真及实验模型。实验系统如图6所示。

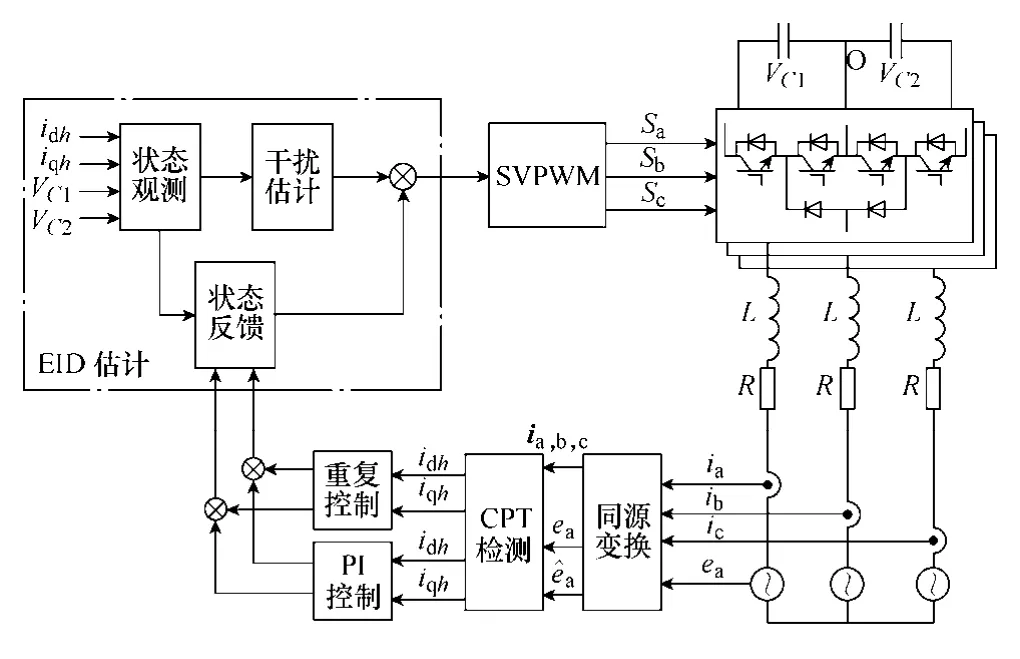
图6 三电平SAPF 控制系统结构图Fig.6 Three-level SAPF control system structure

三电平SAPF 检测电网三相电流、电压及其同源变量，无需坐标变换，经CPT 检测出谐波电流指令，送入控制器中，经EID 控制器滤除干扰后，由三电平SVPWM 调制出开关控制信号，控制三电平SAPF 产生补偿电流，抵消电网电流中谐波分量。图6中谐波源为带电阻负载三相不可控整流器。实验参数见下表。

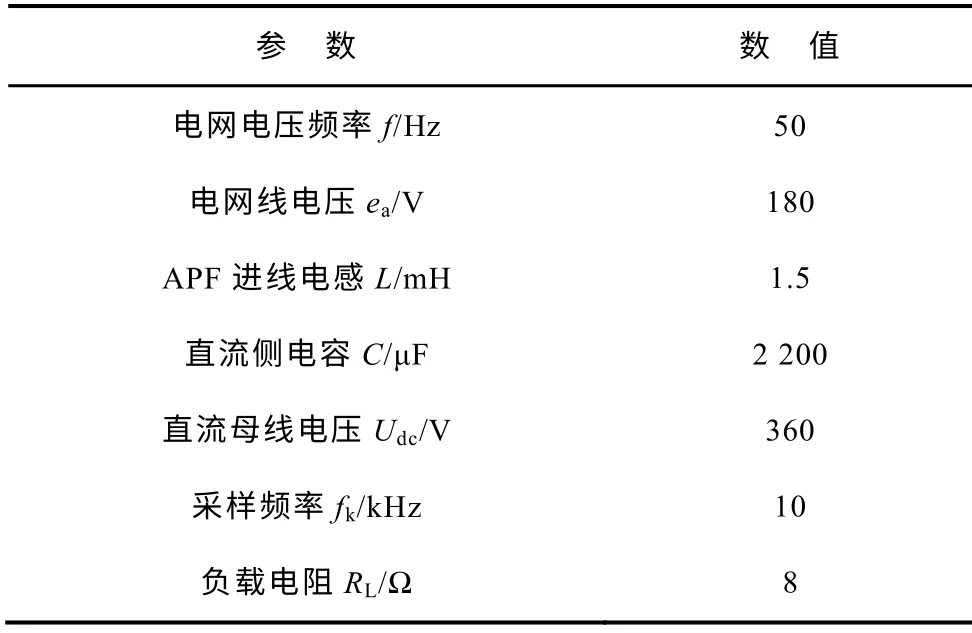
表 三电平SAPF 参数Tab. Parameters of the three-level SAPF

4.1 间谐波检测效果

利用Matlab 对图6搭建系统进行验证，首先验证系统对电网间谐波检测效果，以基于瞬时无功功率理论的ip-iq检测方法作为对比，检测波形基波为50Hz，系统在0.08s时加入频率分别为80Hz、250Hz谐波分量。仿真结果如图7所示。

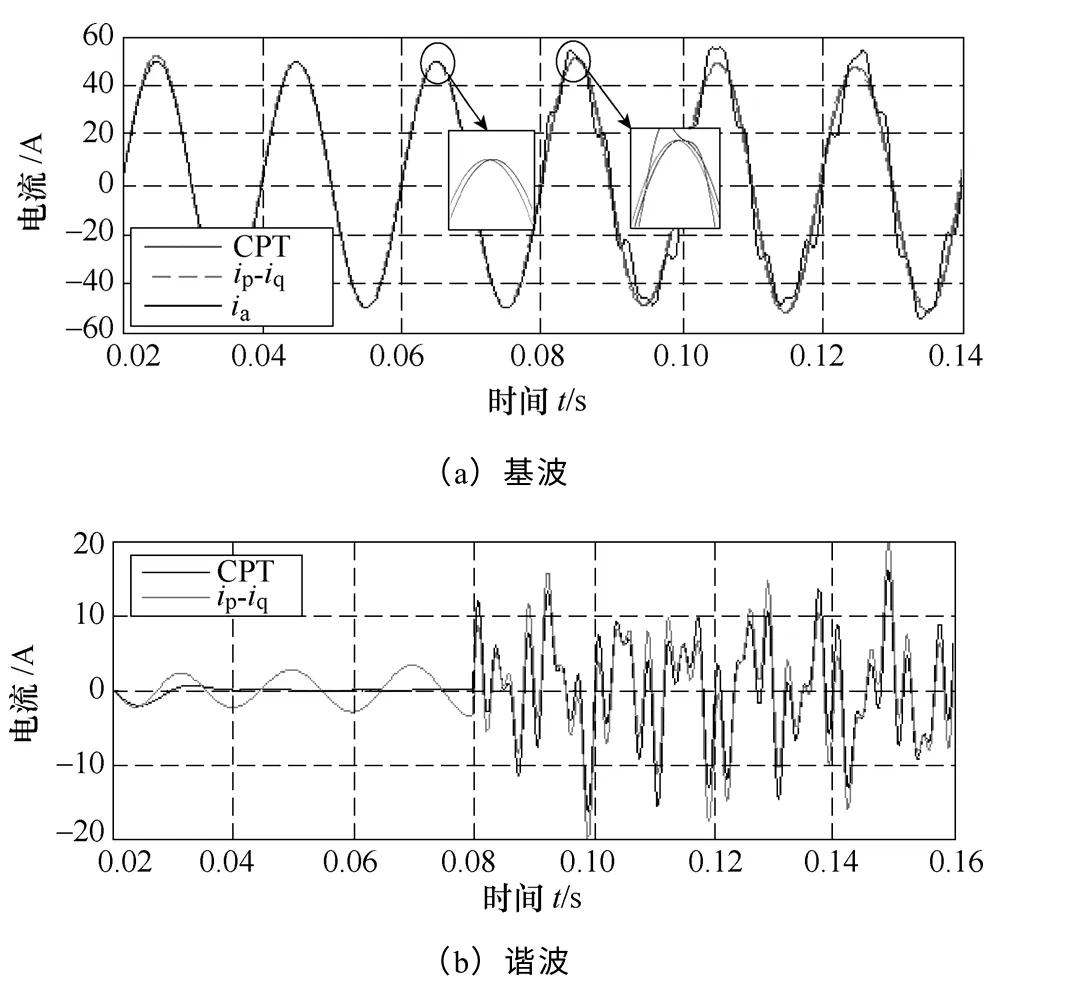
图7 检测波形比较Fig.7 Comparison waveforms of current

图7a 波形分别为检测波形ia，以及基于CPT理论和ip-iq理论检测ia的基波分量。可以看出，在加入谐波前，基于CPT 理论检测基波与ia波形重合，基于ip-iq理论检测波形则有一定相位差，这主要是由瞬时功率检测中的坐标变换引起的[25]。将检测到的基波与ia相减，得到ia中谐波分量，如图7b 所示。可以看出，由于检测基波存在相位偏移等原因，造成最终ip-iq检测谐波含量有放大现象。

4.2 谐波电流补偿效果

利用Matlab 对图6所示系统搭建仿真平台，补偿前电网电流波形如图8a 所示，加入图6所示SAPF补偿后，电网电流波形如图8b 所示。分别对加入EID 和未加入EID 控制的两组系统进行仿真，将补偿电流与检测谐波指令电流相减，得到SAPF 误差电流信号如图8c 所示。可以看出加入EID 控制后，补偿电流较指令电流误差较小，说明加入EID 控制后，控制系统对指令跟踪性能更好。

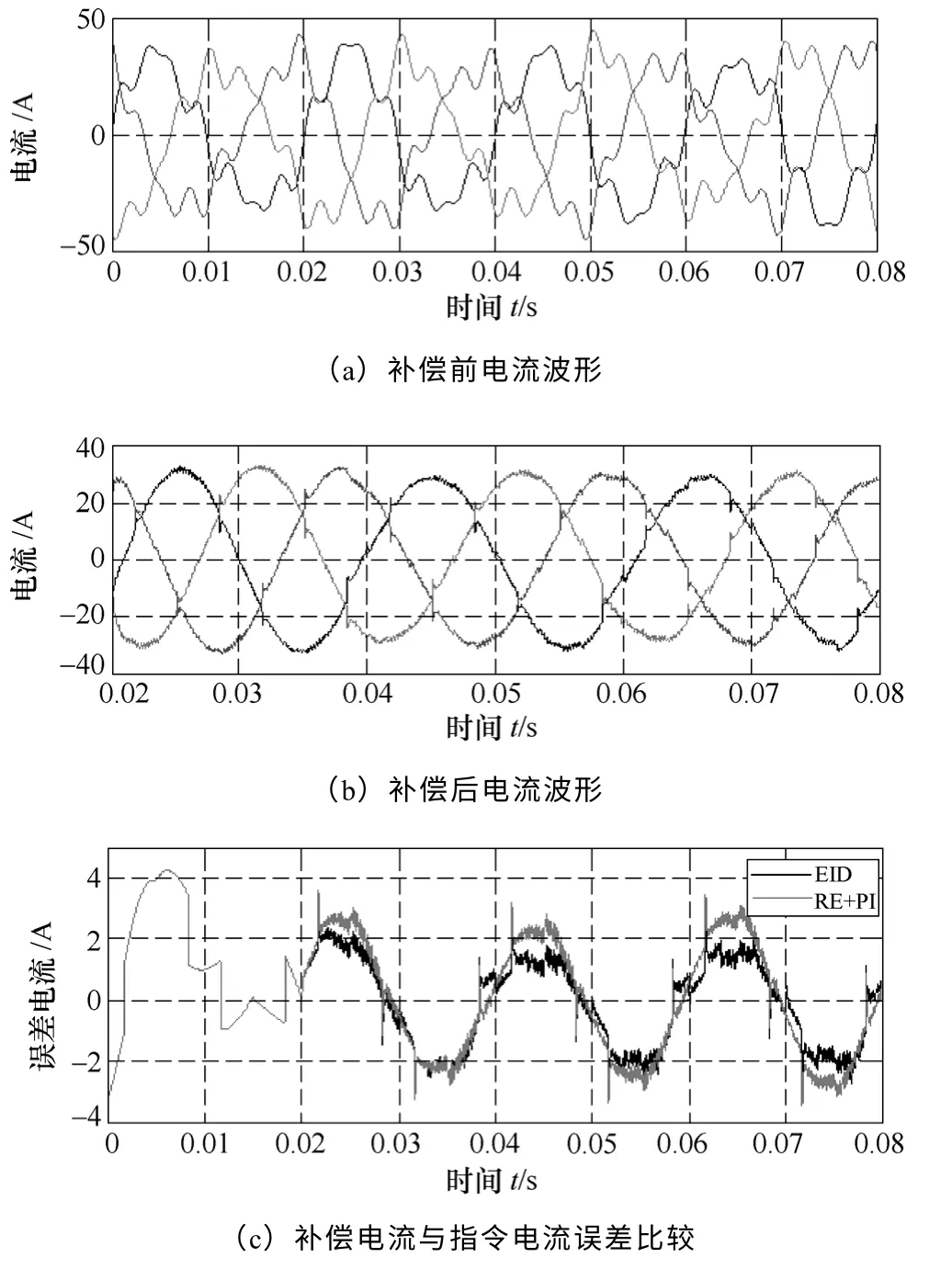
图8 SAPF 谐波补偿效果比较Fig.8 Comparison of SAPF harmonic compensation

图9为以三电平实验平台为依托，利用Fluke电能质量分析仪对电网电流进行检测，得到波形与频谱，实验参数见表。治理前，电网谐波源特征次谐波为5、7 次，同时含有1.5 次间谐波，电网电流波形、频谱分别如图9a、图9b 所示。以重复和PI复合控制的SAPF 进行补偿，间谐波和各次谐波分量有所减少，电网电流波形、频谱分别如图9c、图9d 所示。采用如图6所示SAPF 控制系统进行补偿，得到电网电流波形、频谱分别如图9e、图9f 所示。可以看出，本文所设计系统与单纯采用重复和PI 复合控制相比，谐波治理效果更加明显。

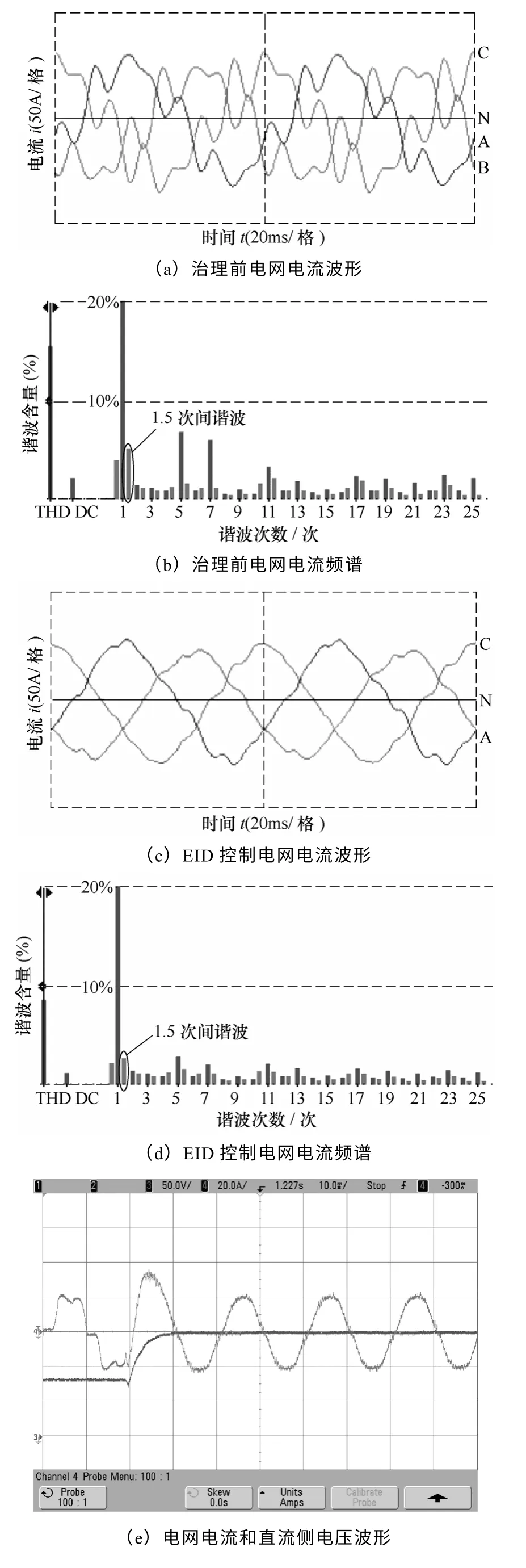
图9 电网电流治理效果对比Fig.9 Comparison of grid current compensation effects

图9e 所示为补偿前后电网电流波形以及直流侧电压波形，可以看出，SAPF 对电网谐波补偿动态性能较好，直流侧电压稳定，证明设计系统可靠。

5 结论

随着新型电力电子设备在电网中应用，电网间谐波影响将会愈发严重。基于瞬时功率理论检测方法存在相位延时、幅值放大等现象，本文以基于CPT功率理论方法对电网间谐波检测，实验证明其有效性。在重复和PI 复合控制基础上，加入EID 干扰推测，提高SAPF 对间谐波控制及对干扰抑制性能，以Matlab 和三电平实验平台对控制系统进行仿真及实验验证，结果证明所设计系统在间谐波环境下可以对电网谐波有效治理，为间谐波环境下电网谐波治理提供思路。

[1]张大海,徐文远.间谐波相序特性的研究[J].中国电机工程学报,2005,25(12):29-34.

Zhang Dahai,Xu Wilsun.Study on the phase sequence characteristics of interharmonics[J].Proceedings of the CSEE,2005,25(12):29-34.

[2]惠锦,杨洪耕.基于间谐波泄漏估算的谐波间谐波分离检测法[J].电工技术学报,2011,26(1):183-190.

Hui Jin,Yang Honggeng.Harmonics and interhar- monics separate-detection method based on estimation of leakage values caused by interharmonics[J].Transac- tions of China Electrotechnical Society,2011,26(1):183-190.

[3]雍静,孙才新,李建波,等.间谐波导致的闪变特征及闪变限制曲线[J].中国电机工程学报,2008,28(31):88-93.

Yong Jing,Sun Caixin,Li Jianbo,et al.Research on thyristor conduction angle characteristics in transient process of TCSC[J].Proceedings of the CSEE,2008,28(31):88-93.

[4]赵伟,罗安,盘宏斌,等.非整数次谐波对混合型有源滤波器性能影响及解决方法[J].中国电机工程学报,2008,28(12):73-78.

Zhao Wei,Luo An,Pan Hongbin,et al.Influence of non-integer harmonics on HAPF and resolution[J].Proceedings of the CSEE,2008,28(12):73-78.

[5]Hsiung C.Inter-harmonic identification using group- Harmonic weighting approach based on the FFT[J].IEEE Transactions on Power Electronics,2008,23(3):1309-1319.

[6]黄纯,朱智军,曹一家,等.一种电网谐波与间谐波分析新方法[J].电工技术学报,2013,28(9):33-39.

Huang Chun,Zhu Zhijun,Cao Yijia,et al.A novel power system harmonic and interharmonic analysis method[J].Transactions of China Electrotechnical Society,2013,28(9):33-39.

[7]赵黎丽.基于相关Hanning 窗插值的间谐波分析算法[J].电工技术学报,2008,23(11):153-158.

Zhao Lili.Inter-harmonics analysis based on correlation Hanning window and interpolation algorithm[J].Transactions of China Electrotechnical Society,2008,23(11):153-158.

[8]赵成勇,何明锋.基于复小波变换相位信息的谐波检测算法[J].中国电机工程学报,2005,25(1):38-42.

Zhao Chengyong,He Mingfeng.A novel method for harmonics measurement using phase information of complex wavelet transform[J].Proceedings of the CSEE,2005,25(1):38-42.

[9]李天云,赵妍,李楠,等.基于HHT 的电能质量检测新方法[J].中国电机工程学报,2005,25(17):52-56.

Li Tianyun,Zhao Yan,Li Nan,et al.A new method for power quality detection based on HHT[J].Procee- dings of the CSEE,2005,25(17):52-56.

[10]马秉伟,刘会金,周莉,等.一种基于自回归模型的间谐波谱估计的改进算法[J].中国电机工程学报,2005,25(15):79-83.

Ma Bingwei,Liu Huijin,Zhou Li,et al.An improved algorithm of interharmonic spectral estimation based on AR model[J].Proceedings of the CSEE,2005,25(15):79-83.

[11]冯宝,樊强,易浩勇,等.基于三线性分解的电力系统谐波与间谐波参数估计算法[J].中国电机工程学报,2013,33(25):173-179.

Feng Bao,Fan Qiang,Yi Haoyong,et al.Harmonic and inter-harmonic parameter estimation algorithm of electric power system based on tri-linear decomposition[J].Proceedings of the CSEE,2013,33(25):173-179.

[12]张宇辉,金国彬,李天云.基于自适应最优核时频分布理论的间谐波分析新方法[J].中国电机工程学报,2006,26(18):84-89.

Zhang Yuhui,Jin Guobin,Li Tianyun.A novel approach to interharmonics analysis based on adaptive optimal kernel time-frequency distribution[J].Procee-dings of the CSEE,2006,26(18):84-89.

[13]吕干云,方奇品,蔡秀珊.一种基于粒子群优化算法的间谐波分析方法[J].电工技术学报,2009,24(12):79-83.

Lü Ganyun,Fang Qipin,Cai Xiushan.A method for inter-harmonics analysis based on PSO[J].Transactions of China Electrotechnical Society,2009,24(12):79-83.

[14]谭智力,李勋,陈坚.基于简化p-q-r 理论的统一电能质量调节器控制策略[J].中国电机工程学报,2007,27(36):85-91.

Tan Zhili,Li Xun,Chen Jian.A new control strategy of UPQC by using simplified p-q-r theory[J].Procee- dings of the CSEE,2007,27(36):85-91.

[15]王茂海,刘会金.通用瞬时功率定义及广义谐波理论[J].中国电机工程学报,2001,21(9):68-73.

Wang Maohai,Liu Huijin.A universal definition of instantaneous power and broad-sense harmonic theory[J].Proceedings of the CSEE,2001,21(9):68-73.

[16]陈东华,谢少军,周波.用于有源电力滤波器谐波和无功电流检测的一种改进同步参考坐标法[J].中国电机工程学报,2005,25(20):62-67.

Chen Donghua,Xie Shaojun,Zhou Bo.An improved synchronous reference frame method for harmonics and reactive currents detection of active power filters[J].Proceedings of the CSEE,2005,25(20):62-67.

[17]孙卓,姜新建,朱东起.电气化铁路中谐波、无功、负序电流的实时检测方法[J].电力系统自动化,2003,27(15):53-57.

Sun Zhuo,Jiang Xinjian,Zhu Dongqi.Detecting methods of reactive power,harmonic and negative- sequence current in electrified rail way systems[J].Automation of Electric Power Systems,2003,27(15):53-57.

[18]郭自勇,周有庆,郭利敏.基于FBD 法的四相输电系统电流检测方法[J].中国电机工程学报,2007,27(22):87-93.

Guo Ziyong,Zhou Youqing,Guo Limin.Current detec- tion for four-phase transmission system based on FBD method[J].Proceedings of the CSEE,2007,27(22):87-93.

[19]Tenti P,Mattavelli P.A time-domain approach to power term definitions under non-sinusoidal conditions[C].Sixth International Workshop on Power Definitions and Measurements under Non-Sinusoidal Conditions,Milano,Italy,2003.

[20]Paredes H.K.M.,Marafao F.P.,da Silva L.C.P.A comparative analysis of FBD,PQ and CPT current decompositions-Part I:Three-phase three-wire systems[C].2009 IEEE Bucharest Power Tech Conference,Bucharest,Romania,2009.

[21]Tenti P,Paredes H.K.M.,Mattavelli P.Conservative power theory,a framework to approach control and accountability issues in smart microgrids[J].IEEE Transactions on Power Electronics,2011,26(3):664- 673.

[22]Pipeleers G,Demeulenaere B,Sewers S.Robust high order repetitive control:optimal performance trade offs[J].Automatica,2008,44(10):2628-2634.

[23]Olm J M,Ramos G A,Costa-Castelló R.Odd- harmonic repetitive control of an active filter under varying network frequency:a small-gain theorem- based stability analysis[C].American Control Con- ference,Baltimore,USA,2010:1060-1068.

[24]She Jinhua,Xin Xin,Pan Yaodong.Equivalent-input- disturbance approach-analysis and application to disturbance rejection in dual-stage feed drive control system[J].IEEE Transactions on Mechatronics,2011,16(2):330-340.