基于离散变速趋近律的模糊滑模高频开关电源控制

焦尚彬 刘 晨 黄伟超 刘 丁 梁炎明

（1.西安理工大学晶体生长设备及系统集成国家地方联合工程研究中心 西安 710048 2.陕西省复杂系统控制与智能信息处理重点实验室 西安 710048）

0 引言

开关电源是通过输出电压反馈和施加有效控制来维持稳定输出电压幅值的装置，广泛应用于工业领域。在实际的控制过程中，由于高频开关电源自身的非线性特点，采用传统的典型控制策略对其进行控制时存在一些不足，例如动态响应特性较慢、不能很好地满足开关电源日益提高的动态响应速度和控制精度的要求[1,2]。因此，寻求更加有效的控制策略来改善开关电源的性能，具有重要的理论意义和实际应用价值。

变结构控制出现于20 世纪50年代，经历了多年发展，已经形成了一个相对独立的研究分支。其核心思想是迫使系统在一定特性下沿规定的状态做小幅度、高频率的上下运动，即所谓的“滑模”运动[3]。变结构控制不需要准确的模型和参数估计，具有算法简单、抗干扰能力强和容易在线优化等优点，适用于不确定非线性多变量的控制对象。因此，滑模变结构等非线性控制理论被越来越多地引入非线性系统的控制策略中。目前，国内外学者使用滑模变结构控制成功地解决了一些实际的非线性系统控制问题。文献[4]将滑模变结构控制方法应用于电机的控制中。文献[5,6]将滑模变结构控制方法应用于DC-DC 开关变换器的控制中。文献[7]将滑模变结构控制应用于有源滤波器的控制中。文献[8]将滑模变结构控制方法应用于逆变器的控制中，均取得了较好的控制效果。上述研究成果为该控制方法应用于结构更复杂的开关电源系统提供了可能。

然而，由于离散滑模变结构控制自身的缺点，要真正发挥其鲁棒性，必须要对传统的离散滑模变结构控制方法进行改进，设计出新型的离散滑模变结构控制器，将有害的抖振减小到一定程度。现有的改进方法包括采用变速趋近律[8,9]、准滑模变结构控制[10]、全局滑模控制[11]、神经滑模变结构控制[12]、间接滑模变结构控制[13]和新的滑模切换面方程[14]等，这些方法均在一定程度上改善了控制器的性能。

本文以高频开关电源为研究对象，设计了一种基于模糊滑模变结构控制的开关电源控制器。论文首先通过准线性建模方法对高频开关电源进行系统建模，以克服采用状态空间平均法建模时工作参数只能在额定工作点附近变化的不足；然后在此模型基础上设计基于变速趋近律的模糊滑模变结构控制器。该控制器将模糊控制和传统滑模变结构控制相结合，简化了模糊控制器的输入，同时柔化了控制信号，减轻了一般滑模变结构控制的抖振现象。另外变结构控制中使用了基于变速趋近律的控制率，既保证了系统的渐近稳定性，又减小了系统的抖动。通过仿真工具进行系统仿真，对比了模糊滑模变结构控制和一般滑模变结构控制在开关电源系统中的控制效果。并且将该方法应用在搭建的1.2kW 移相全桥开关电源的控制中，实验结果验证了文本所提出控制方法的有效性。

1 移相全桥开关电源的准线性模型

状态空间平均法规定变换器参数只能在额定工作点附近变化，对于要求工作参数变化较大的移相全桥开关电源来说，采用该方法建模不是很有效。针对状态空间平均法建模的不足，文献[15-17]提出了准线性建模方法。移相全桥开关电源拓扑结构如图1所示。本文采用准线性建模方法来对移相全桥开关电源进行系统建模。所建模型由两部分组成：①扰动模型描述了系统在稳定状态下的暂态响应特性；②稳定点模型描述了系统在某些输入电压和负载情况下具有变化的稳定特性。该模型围绕变化的工作点作扰动，采用系统小信号差分状态方程来 表述。

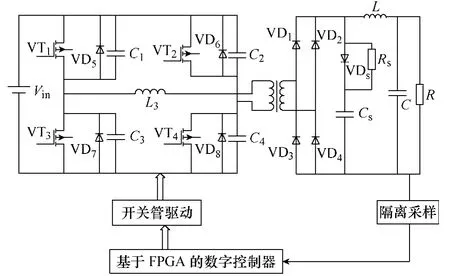
图1 移相全桥开关电源拓扑结构Fig.1 Topology of phase-shift full bridge switching power supply

1.1 准线性小信号扰动模型

移相全桥开关电源工作状态随开关管的通断在不同模态间切换。定义开关函数

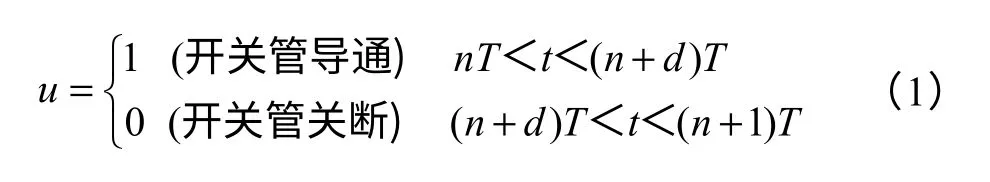
式中，T为开关周期；d为占空比函数。其小信号模型如图2所示。

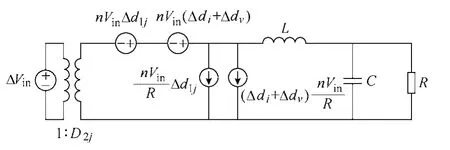
图2 移相全桥开关电源小信号模型Fig.2 Small signal model of phase-shift full bridge switching power supply

图2中Δdi为滤波电感电流变化引起的占空比扰动量Δde的变化量，其中Δde=Δd1j+Δdi+Δdv；Δdv为输入电压变化引起的Δde的变化量；Δd1j为变压器初级占空比引起的Δde的变化量；ΔVin为输入电压扰动量；D2j为变压器二次电压的占空比；de为有效占空比，de=D2j+Δde；L为滤波电感；R为负载电阻；C为滤波电容。

建立移相全桥开关电源的准线性小信号扰动模型时，若作线性化扰动的变量只包括电感电流IL、电容电压VC及占空比d，这样移相全桥变换器的稳态工作点就随输入电压Vin的变化而变化。另外，如果不考虑输入电压Vin的变化对有效占空比扰动量Δde的影响，就可以得出其准线性小信号扰动模型，如图3所示。

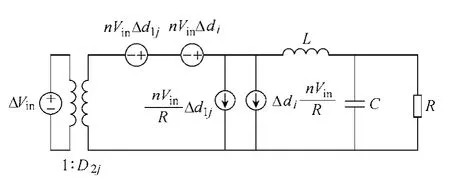
图3 移相全桥开关电源准线性小信号扰动模型Fig.3 Quasi linear small signal disturbance model of phase-shift full bridge switch power supply

准线性小信号扰动模型的状态方程表达式为

式中，x(t)为状态变量，包括小信号滤波电感电流IL和小信号滤波电容电压VC两个状态变量，分别等于IL和输出电压Uo与其设定值之差；du为小信号占空比扰动输入；Uo(t)为输出电压；n为变压器二次侧与一次侧匝数比；L1为谐振电感；fs为开关频率；L为滤波电感；R为负载电阻；C为滤波电容。

离散化后可得其差分方程为

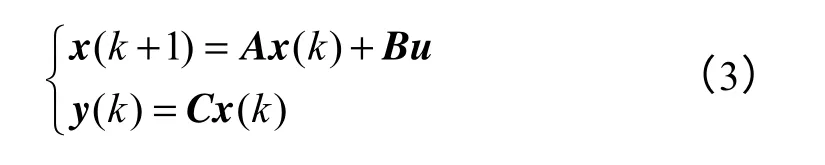
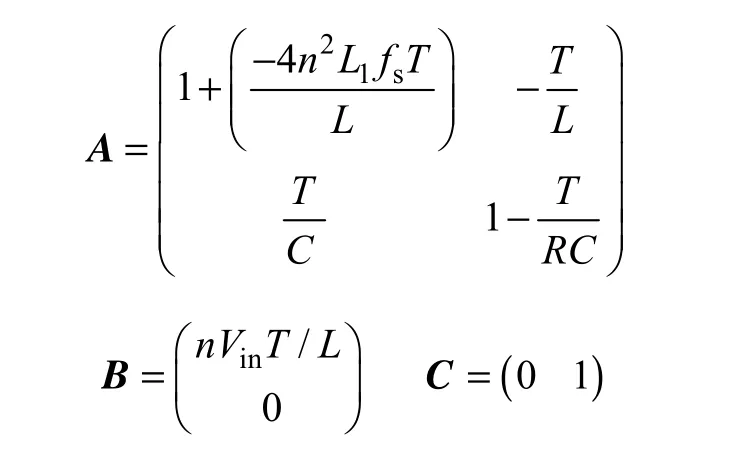
式中，T为采样周期。

1.2 稳态工作点模型

开关电源大多要求输出电压oU为一个稳定的值。由于系统中的滤波电容C并没有串联电阻，则电容电压VC就等于输出电压oU，电感电流LI等于负载电流oI，移相全桥变换器在稳定工作时的占空比可表示为系统稳定点状态变量和系统输入电压的函数。移相全桥变换器工作过程中会有占空比丢失，有效占空比为变压器二次侧占空比2jD，2jD和 丢失占空比DΔ 可分别表示为

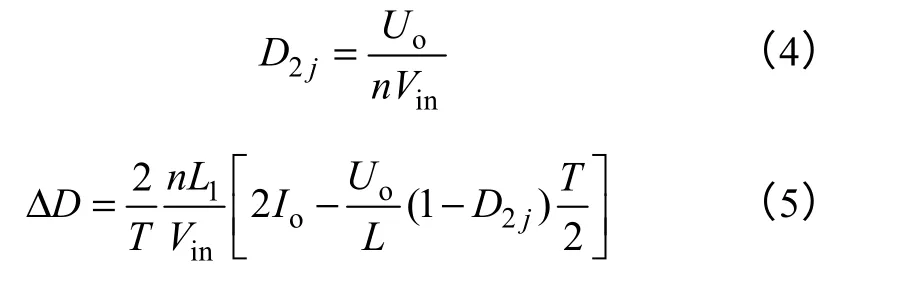
式中，T为开关周期。

一次侧占空比1jD可表示为

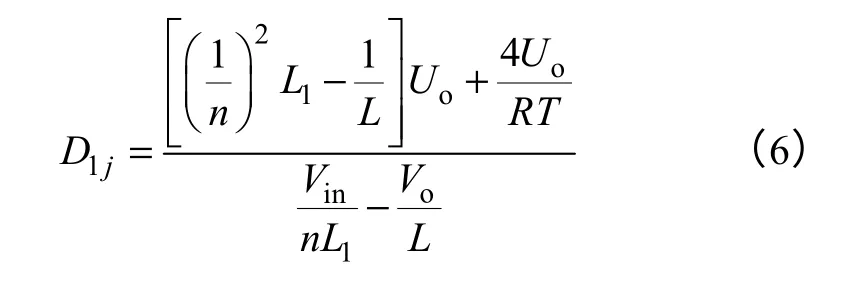
由式（6）可见，1jD是随输入电压inV的变化而变化的，所以对输入电压inV的扰动具有很强的抑制作用，能有效地保证系统在扰动下保持稳定。

2 离散模糊滑模变结构控制器的设计

滑模变结构控制为不确定性的对象提供了一种确定性的控制系统设计方法，利用该方法可以设计出结构简单的控制器。滑动模态可以按照要求来设计，系统的滑模运动受控制对象的参数变化和系统外界的干扰影响较小，所以滑模变结构控制系统的鲁棒性很强。但是，该方法存在如下缺点：①当状态轨迹到达滑模面后，运动点难于严格地沿着滑模面向平衡点滑动，而是在滑模面两侧往复运动；②滑模变结构控制自身存在不连续开关特性，在光滑的滑模面上会叠加一个锯齿形的轨迹。上述缺点会形成系统抖振。如果消除了抖振也就消除了变结构控制的抗扰动能力，因此抖振只能在一定程度上削弱。

模糊滑模变结构控制将模糊控制和传统的滑模变结构控制相结合，使不连续的控制信号连续化,可以解决滑模变结构控制中的高频颤动问题[18]。模糊滑模变结构控制将控制目标从跟踪误差转为滑模函数，只要施加控制使滑模函数s为零，跟踪误差将渐近到达零点。另外对于二阶以上的高阶系统，模糊滑模变结构控制的输入始终是二维的[19]。

2.1 滑模变结构控制超平面和控制率的选取

模糊滑模变结构控制系统结构如图4所示。本文系统的状态方程如式（3）所示。

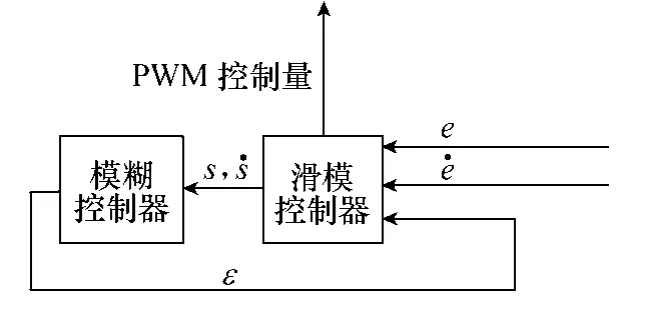
图4 模糊滑模变结构控制器结构框图Fig.4 Structure diagram of fuzzy sliding mode control system

设定值为r(k)、设定值的导数为dr(k)，x(k)=(x1(k),x2(k))，其中x2(k)=dx1(k)，令R(k)=(r(k),dr(k))，R(k+1) =(r(k+1),dr(k+1))，对r(k+1)和dr(k+1)采用线性外推的方法进行推导。

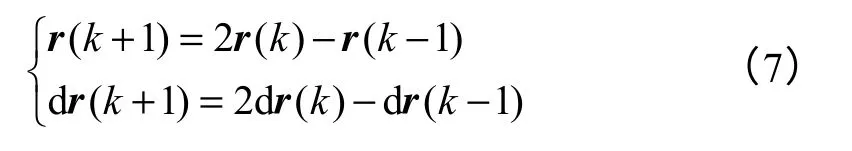
取切换函数为动态非线性滑模面形式

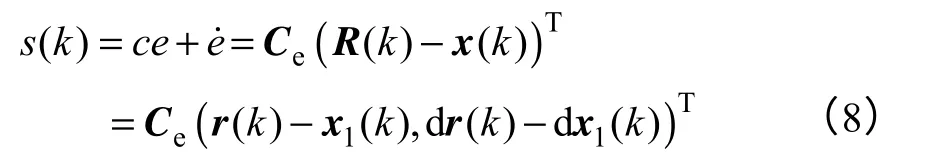
式中，e为系统偏差；为系统偏差的导数，偏差矩阵。参数c称为滑模系数，描述了滑模面的斜率，能够影响滑模运动的渐近稳定性和动态响应性能。滑模面参数c越大，滑模运动段响应越快，快速性越好，但是参数c过大会使输出控制量过大，引起系统抖振，所以要通过后文中的计算确定出合适的滑模系数。

为了使式（8）中滑模面方程上下对应，定义Ce=(c,1)。

利用式（8）得到s(k+1)的表达式为

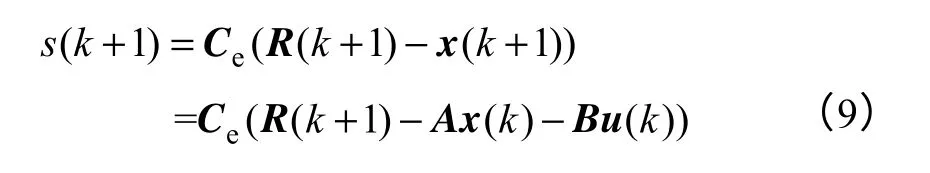
推导求得控制率为

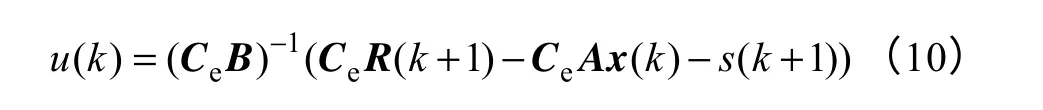
基于指数的离散趋近律为

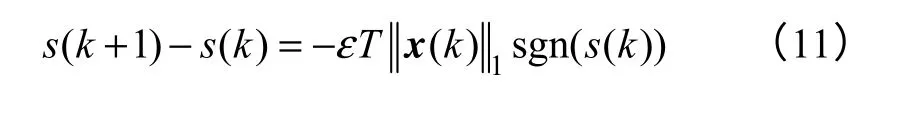
故基于变速趋近律的离散控制率为

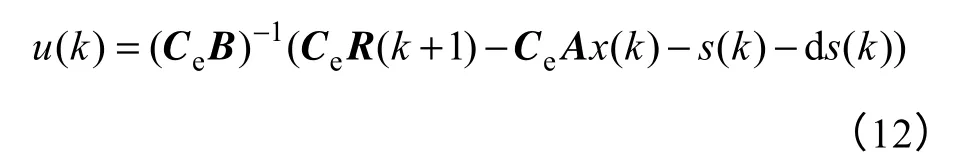
2.2 滑模切换参数的确定

离散滑模变结构控制出现了滑模切换区，在切换区中发生准滑动模态运动[20]。定义新的变量，则

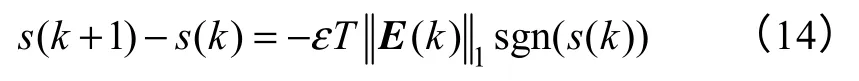
由式（14）可以得到

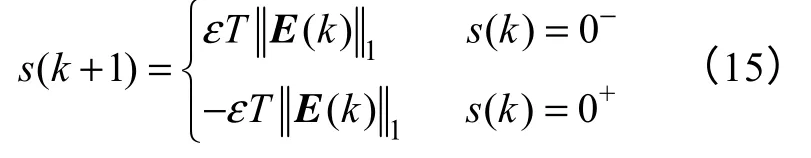
式（15）中的两条过原点的射线组成了扇形的滑模切换区，将滑模面 0s=包含在其中，如图5所示。定义切换区为，切换区厚度为2Δ。可得，所以

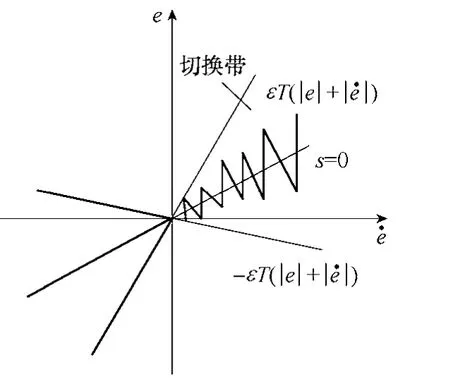
图5 滑模切换区示意图Fig.5 Map of sliding mode switching area

考虑式（16）的值，当s(k)＞0时

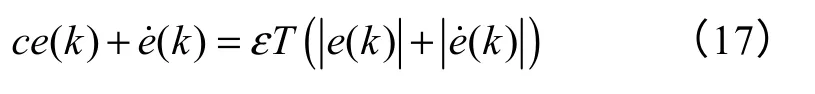
当s(k)＞0时

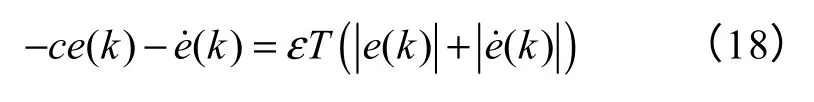
对式（17）消去绝对值，可以化简为

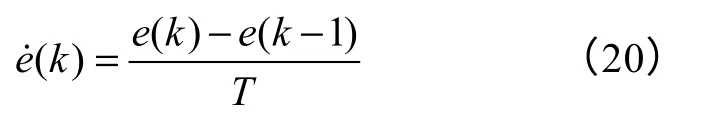
联立式（19）和式（20）得出

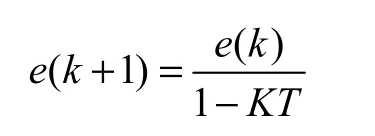
为了使系统能渐近收敛到原点，(k)e前面系数的取值必须被限制在（−1，1）中，由此可得

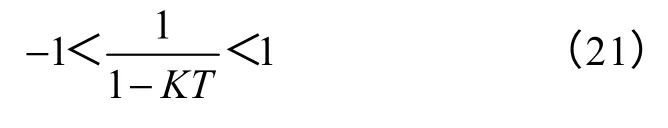
式（18）分为4 种情况

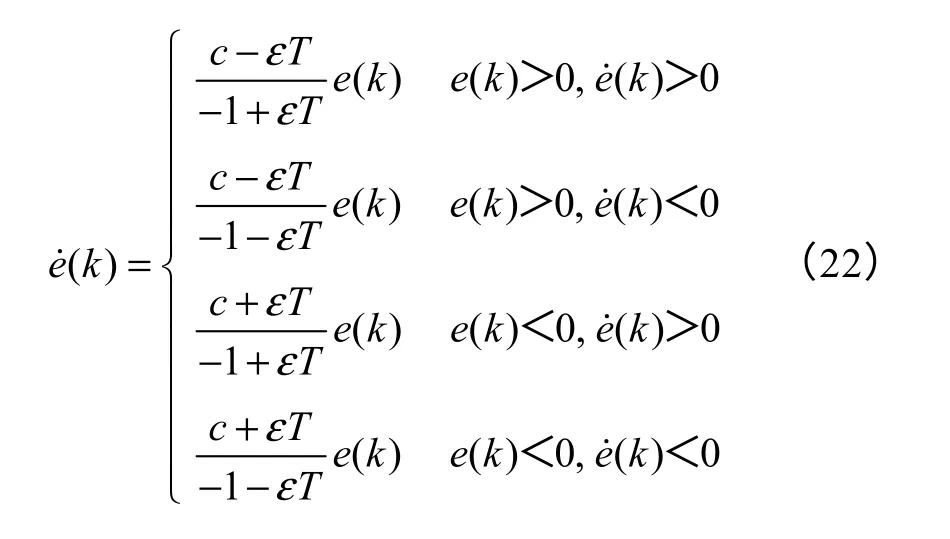
假设0 1Tε＜ ＜，联立式（21）、式（22）可解得，滑模超平面系数的范围为

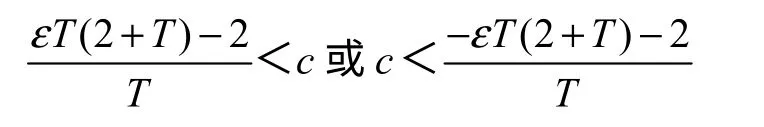
同理，式（18）有一样的结论。

2.3 模糊控制器的设计

设计一个二输入单输出的模糊控制器，取切换函数的误差s(k) 及其变化率作为模糊控制器输入，s(k)→ 0，滑模控制率中的参数ε作为输出变量。模糊语言集合均为7 个模糊子集：PB（正大）、PM（正中）、PS（正小）、ZO（零）、NS（负小）、NM（负中）和NB（负大），论域元素的取值范围为[−6，6]，采用三角形隶属度函数，如图6所示。通过模糊规则进行模糊推理。模糊推理规则见下表，在采样时间固定的条件下，模糊控制器输出ε值决定了控制器抖振的幅度。

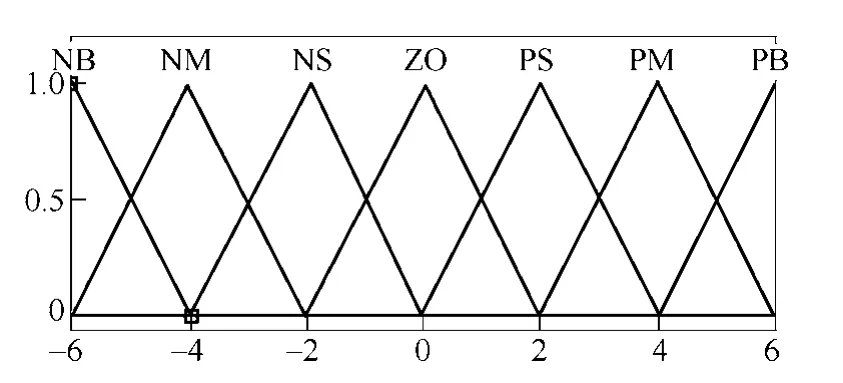
图6 隶属度函数设计Fig.6 The design map of membership function

定义一个Lyapounov 函数

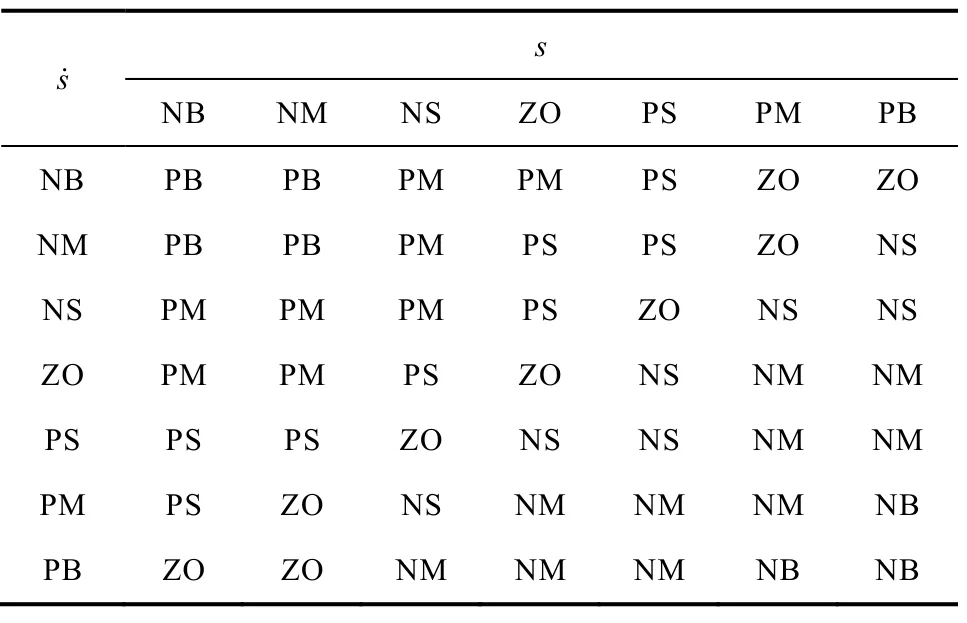
表 模糊推理规则表Tab. Fuzzy inference rules

3 系统仿真及实验验证

3.1 系统仿真参数

为了验证上述模糊滑模变结构控制器的效果，针对全桥逆变高频开关电源，参数选取如下：切换函数为，其中控制率中c=4.5。电源输入电压Vin=220V，开关频率fs＝20kHz，阻性负载R=5Ω，滤波电感L=1mH。分别在启动过程、电压扰动和负载扰动时对比模糊滑模变结构控制与一般滑模变结构控制的动态响应性能。

3.2 系统启动响应

电压设定值为60V、阻性负载条件下，模糊滑模变结构控制与一般滑模变结构控制的启动响应结果比较如图7所示。其中，图7a 为模糊滑模变结构控制的启动响应波形，图7b 为滑模变结构控制的启动响应波形。为了便于比较，在小图中给出局部波形放大4 倍时的效果图。模糊滑模变结构控制的调节时间为0.004s，快于一般滑模变结构控制0.009s，且模糊滑模变结构控制的波形稳定性较好，抖振幅度为0.05V，纹波系数为0.12%。一般滑模变结构控制抖振较严重，抖振幅度为0.25V，纹波系数为0.59%。

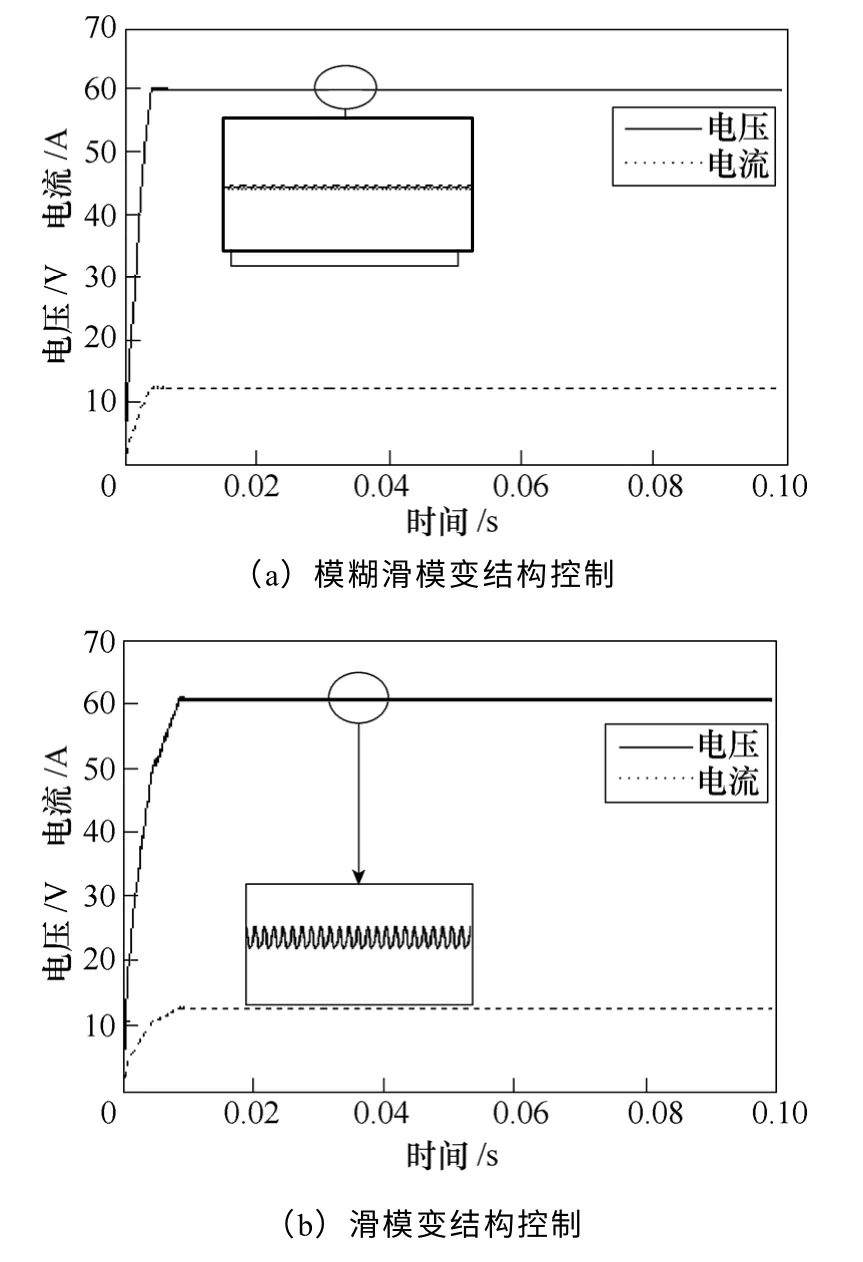
图7 两种控制方法输出电压和电流启动波形Fig.7 Two controllers output voltage and current starting waveforms comparison

3.3 电压扰动下动态响应

图8为阻性负载条件下，电压设定值周期性地在60V 与80V 之间变化时，模糊滑模变结构控制与一般滑模变结构控制结果比较。其中，图8a 为电压扰动时刻及幅值示意图，图8b 为电压扰动下模糊滑模变结构控制的动态响应波形，图8c 为电压扰动下滑模变结构控制的动态响应波形。在电压扰动的时刻，模糊滑模变结构控制波形过渡光滑，尤其在电压突变减小的时刻，一般滑模变结构控制响应波形出现较大波动，调节时间为0.004s，模糊滑模变结构控制响应波形则波动较小，且调节时间为0.001s，无超调。

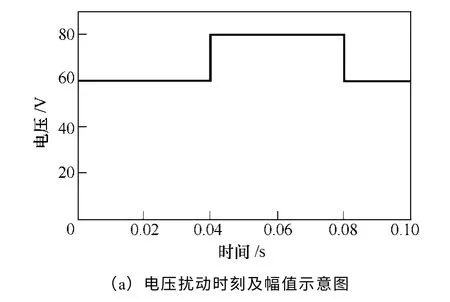
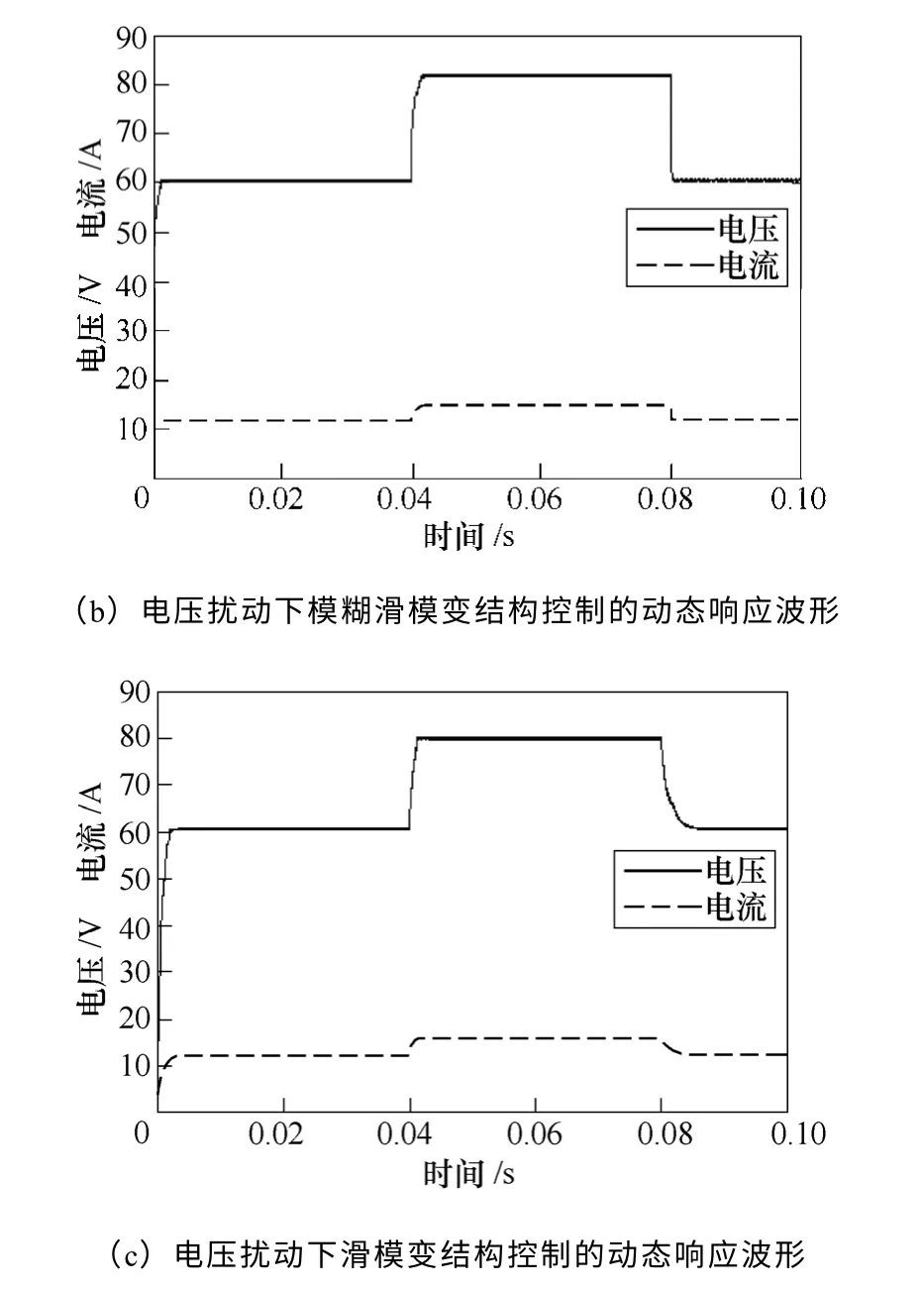
图8 两种控制方法在电压扰动下输出电压和 电流动态响应波形Fig.8 Two controllers output voltage and current dynamic response waveforms with input voltage disturbance

3.4 负载电压扰动下动态响应

图9为阻性负载周期性在5 Ω 和10 Ω 之间的变化时，模糊滑模变结构控制与一般滑模变结构控制结果比较。其中，图9a 为负载扰动时刻及幅值示意图，图9b 为负载扰动下模糊滑模变结构控制的动态响应波形，图9c 为负载扰动下滑模变结构控制的动态响应波形。从图9可以看出，当负载跳变时，一般滑模变结构控制响应波形出现较大波动，提高负载和降低负载时动态超调幅度分别为10V、6.3V；模糊滑模变结构控制响应波形波动较小，提高负载和降低负载时动态超调幅度分别为1.7V、1.9V。同时系统在重新到达稳定状态时，模糊滑模变结构控制对应于两次切换负载所用的时间分别为0.000 3s、0.006s，而一般滑模控制所用的时间分别为0.012s、0.008s。

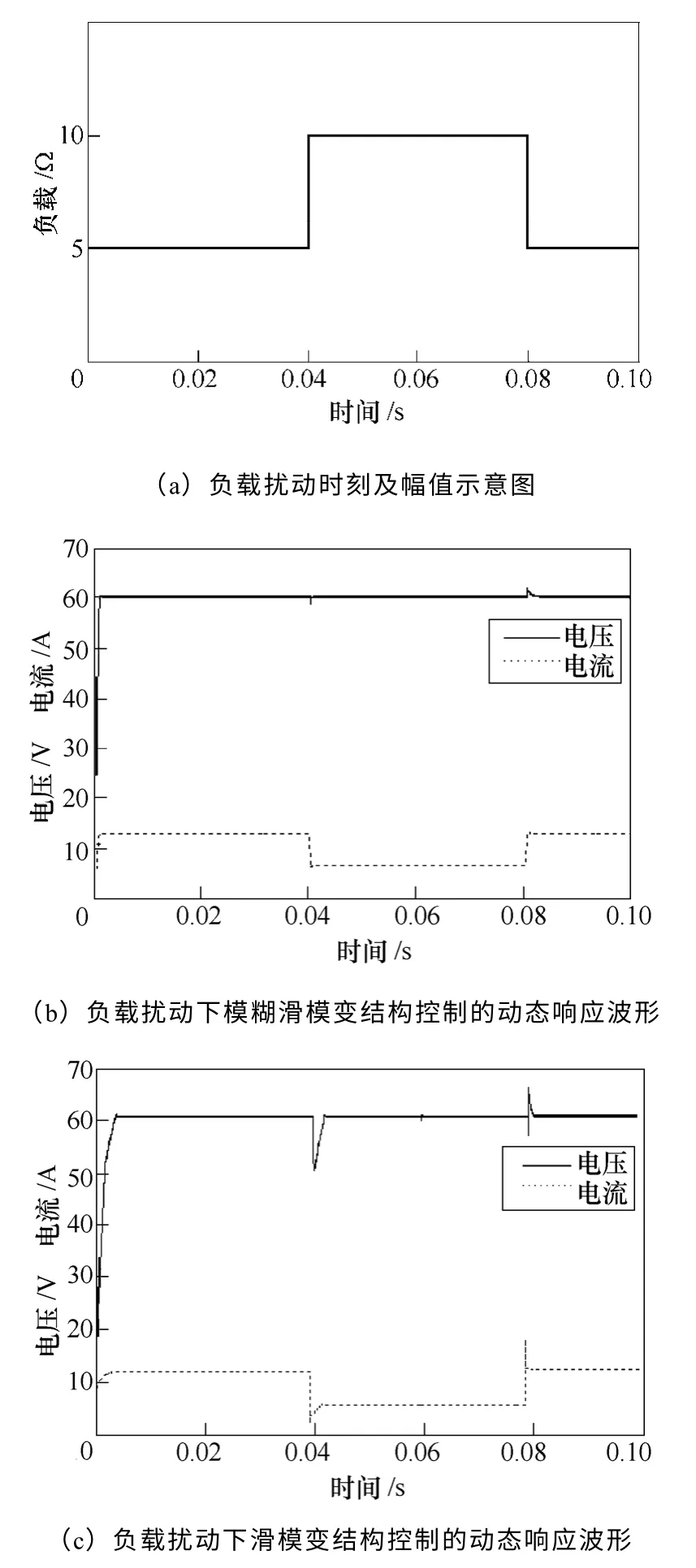
图9 两种控制方法在负载扰动下输出电压和 电流动态响应波形Fig.9 Two controllers output voltage and current dynamic response waveforms with load disturbance

3.5 电感值扰动下的鲁棒性

图10为电压设定值60V、感性负载条件下，负载电感值分别为1mH、3mH 和5mH时，模糊滑模变结构控制与一般滑模变结构控制启动响应波形比较图。其中，图10a 为电感值情况下模糊滑模变结构控制启动响应波形，图10b 为不同电感值情况下滑模变结构控制启动响应波形。从图10中可以看出，当负载电感值分别为1mH、3mH 和5mH时，一般滑模变结构控制对应的调节时间分别为0.027s、0.045s 和0.067s，抖振幅度分别为0.075V、 0.09V 和0.1V；模糊滑模控制对应的调节时间分别为0.025s、0.032s 和0.05s，抖振幅度分别为0.002 5V，0.003 5V 和0.005V。

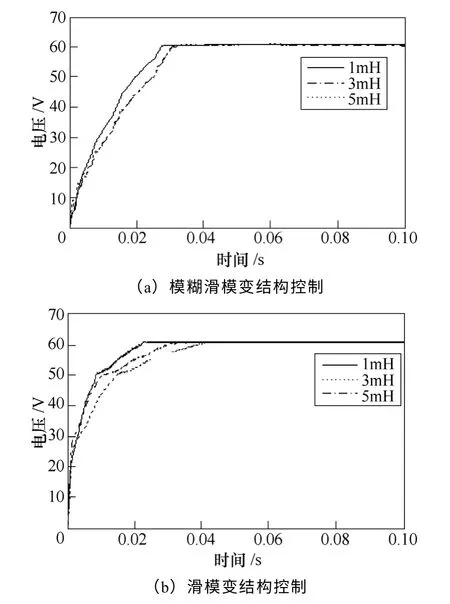
图10 两种控制方法在不同电感值下的 启动响应波形Fig.10 Two controllers starting response waveform with different inductor

因此，模糊滑模控制相比于一般滑模控制，调节速度更快，抖振幅度更小，鲁棒性更强。

3.6 实验验证

为了验证所提出的准线性建模和模糊滑模控制方法的正确性，设计了基于 Xilinx XC3S500E Spartan—3E FPGA 的控制系统，针对1.2kW 移相全桥开关电源样机进行了模糊滑模控制与一般滑模控制的对比实验研究。样机中使用M57962L 驱动电路驱动IGBT 开关管，ADS8361 作为模数转换器，功率芯片TOP244 作为辅助电源，对IGBT 正负双电压供电。开关频率为20kHz，输出滤波电感1mH，滤波电容2mF。

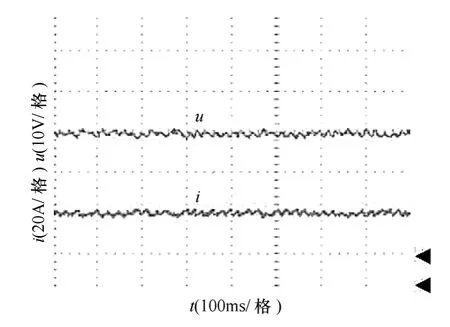
图11 一般滑模变结构控制系统的输出电压和 电流稳态响应实验波形Fig.11 Steady-state output voltage and current response experiement waveforms of sliding mode variable structure controller

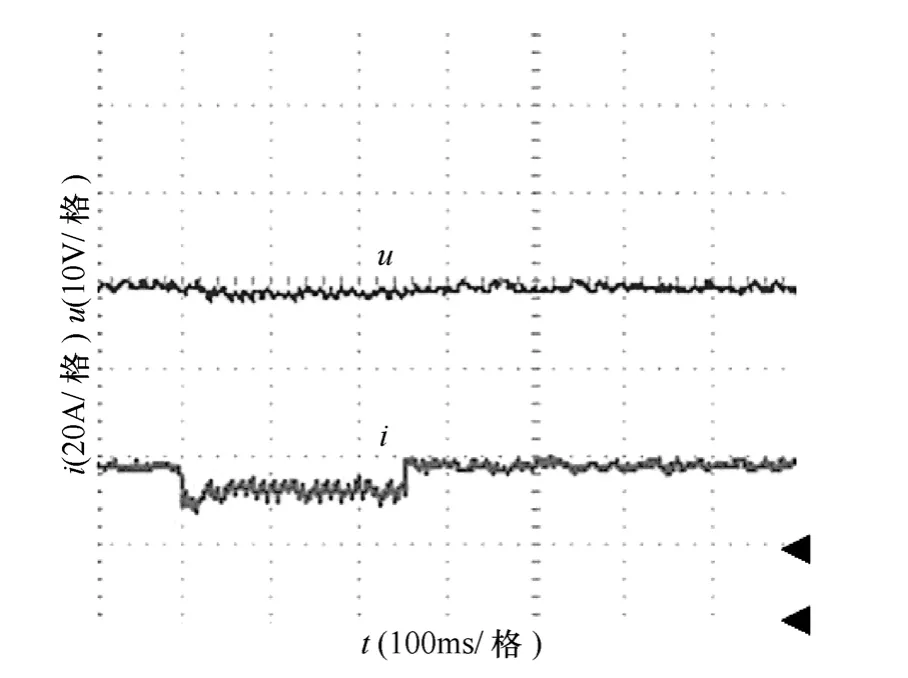
图12 一般滑模变结构控制系统在负载扰动下 输出电压和电流动态响应实验波形Fig.12 Output voltage and current dynamic response experiement waveforms of sliding mode variable structure controller with load disturbance

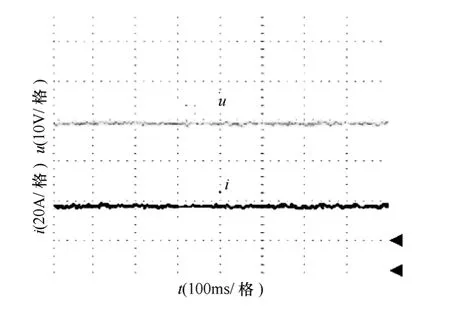
图13 模糊滑模变结构控制系统的输出电压和 电流稳态响应实验波形Fig.13 Steady-state output voltage and current response experiement waveforms of fuzzy sliding mode variable structure controller

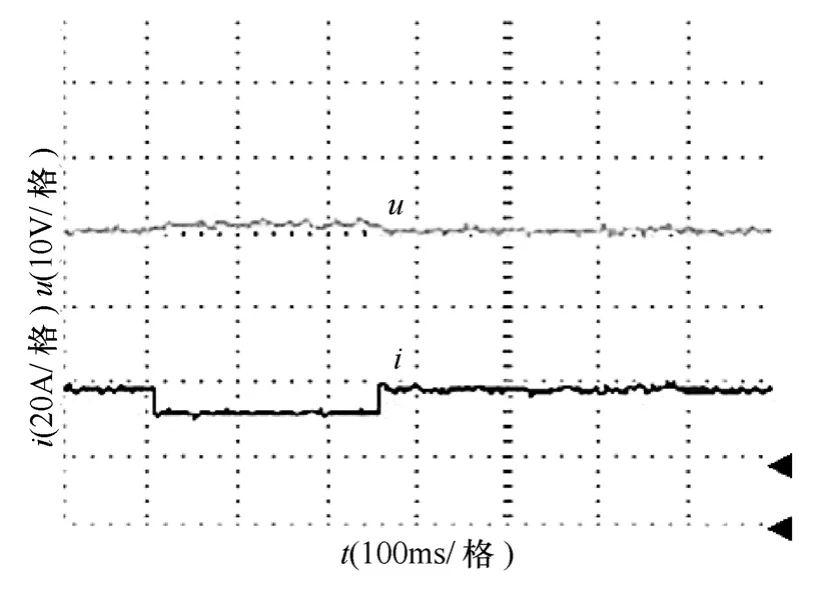
图14 模糊滑模变结构控制系统在负载扰动下 输出电压和电流动态响应实验波形Fig.14 Output voltage and current dynamic response experiemnet waveforms of fuzzy sliding mode variable structure controller with load disturbance

图11为一般滑模变结构控制系统稳态时的输出电压（40V）和电流（20A）波形。图12为一般滑模变结构控制系统的负载在40V/20A 到40V/10A之间周期性变化时，输出电压和电流波形。图 13为模糊滑模变结构控制系统稳态时的输出电压（40V）和电流（20A）波形。图14为模糊滑模变结构控制系统的负载在40V/20A 到40V/10A 之间周期性变化时，输出电压和电流波形。图11～图14中下方的箭头均为电压的零点，上方的箭头均为电流的零点。分析计算可知，一般滑模变结构控制和模糊滑模变结构控制系统的抖振幅度分别为 0.8V和0.15V，纹波系数分别为1.41%和0.27%。一般滑模变结构控制提高负载和降低负载时动态超调幅度分别为2.5V 和2V，动态稳定时间分别为0.06s 和0.04s；模糊滑模变结构控制提高负载和降低负载时动态超调幅度分别为1V 和1.5V，动态稳定时间都为0.02s。说明采用模糊滑模变结构控制方法后，系统的抖振幅度减小，动态响应速度快，鲁棒性强，与仿真结果一致。

4 结论

本文设计了一种适用于高频开关电源系统的模糊滑模变结构控制器。首先采用准线性建模方法对移相全桥高频开关电源进行了系统建模，然后选取了线性切换函数和基于变速趋近律的滑模变结构控制率，确定了相应的模糊控制规则，分析了使得系统能够渐近稳定于原点的滑模切换区范围以及滑模超平面系数的选取范围，得到了高频开关电源模糊滑模变结构控制器。通过仿真分析比较及实验验证，结果证明所设计的控制器具有良好的动态响应特性和强鲁棒性。在系统参数突变的情况下，调节速度快于一般滑模变结构控制器，同时保证了系统的稳定性，减轻了系统的抖振，改善了系统的性能。

[1]邓卫华,张波,胡宗波,等.CCM Buck 变换器的状态反馈精确线性化的非线性解耦控制研究[J].中国电机工程学报,2004,24(5):120-125.

Deng Weihua,Zhang Bo,Hu Zongbo,et al.Research of nonlinear decoupled control law using state variable feedback linearization method based on the CCM Buck converter[J].Proceedings of the CSEE,2004,24(5):120-125.

[2]邓卫华,张波,丘东元,等.电流连续型Boost 变换器状态反馈精确线性化与非线性PID 控制研究[J].中国电机工程学报,2004,24(8):45-50.

Deng Weihua,Zhang Bo,Qiu Dongyuan,et al.The research of state varible feedback linearization method on the CCM Boost converter and nonlinear PID control law[J].Proceedings of the CSEE,2004,24(8):45-50.

[3]刘金琨.滑模变结构控制MATLAB 仿真[M].北京:清华大学出版社,2005.

[4]朱喜华,李颖晖,张敬.基于一种新型滑模观测器的永磁同步电机无传感器控制[J].电力系统保护与控制,2010,38(13):6-10.

Zhu Xihua,Li Yinghui,Zhang Jing.Sensorless control of PMSM based on a novel sliding mode observer[J].Power System Protection and Control,2010,38(13):6-10.

[5]倪雨,许建平.控制受限滑模控制BUCK 变换器优化设计[J].电子学报,2013,41(3):555-560.

Ni Yu,Xu Jianping.Optimal design of sliding mode control BUCK converter with bounded input[J].Acta Electronica Sinica,2013,41(3):555-560.

[6]何金梅,郑雪梅,王卫,等.Boost 变换器混沌现象的非奇异终端滑模控制方法[J].电工技术学报,2013,28(4):104-108.

He Jinmei,Zheng Xuemei,Wang Wei,et al.Terminal sliding mode control of Boost converter with chaos[J].Transactions of China Electrotechnical Society,2013,28(4):104-108.

[7]胡志坤,张乾,刘守明,等.三相并联型有源滤波器的滑模控制方法[J].电工技术学报,2011,26(12):122-128.

Hu Zhikun,Zhang Qian,Liu Shouming,et al.Sliding mode control method of three phase shunt active power filter[J].Transactions of China Electrotechnical Society,2011,26(12):122-128.

[8]吴忠强,庄述燕,马宝明,等.基于逆系统方法的并网逆变器自适应模糊滑模控制研究[J].电力系统保护与控制,2011,39(24):1-7.

Wu Zhongqiang,Zhuang Shuyan,Ma Baoming,et al.Research on adaptive fuzzy sliding mode control for grid-connected inverter based on inverse system[J].Power System Protection and Control,2011,39(24):1-7.

[9]蒋栋年,李炜,王君.一类离散非线性时延系统的滑模变结构控制研究[J].计算机应用研究,2013,30(7):1971-1974.

Jiang Dongnian,Li Wei,Wang Jun.Variable-structure control with sliding mode for discrete nonlinear time delay system[J].Application Research of Computers,2013,30(7):1971-1974.

[10]倪雨,许建平.准滑模控制开关 DC-DC 变换器分析[J].中国电机工程学报,2008,28(21):1-6.

Ni Yu,Xu Jianping.Quasi-sliding-mode switching control for DC-DC converters[J].Proceedings of the CSEE,2008,28(21):1-6.

[11]王鲜芳,杜志勇,王向东.基于LS-SVM 和滑模变结构的无刷直流电动机混合控制[J].电力系统保护与控制,2011,39(2):70-74.

Wang Xianfang,Du Zhiyong,Wang Xiangdong.Hybrid control of brushless DC motor based on LS-SVM and sliding mode variable structure[J].Power System Protection and Control,2011,39(2):70-74.

[12]蔚永强,郭宏,谢占明.直驱式伺服系统的神经网络自适应滑模控制[J].电工技术学报,2009,24(3):74-79.

Yu Yongqiang,Guo Hong,Xie Zhanming.Neural network adaptive sliding mode control for direct- drive servo system[J].Transactions of China Electro- technical Society,2009,24(3):74-79.

[13]Nguyen V M,Lee C Q.Indirect implementations of sliding-mode control law in Buck-type converters[C].Eleventh Annual IEEE Applied Power Electronics Conference and Exposition,1996,1:111-115.

[14]Geng J,Zhang C,Luo C.Research of a PWM-based new sliding-mode controller for the Buck converter[C].2nd IEEE Conference on Industrial Electronics and Applications,ICIEA 2007:1907-1911.

[15]Tse C K,Tam C Y.A quasi-linear controller for DC/DC converter using a TMS320 digital signal processor[C].25th Annual IEEE Power Electronics Specialists Conference,1994:1040-1045.

[16]VlatkoviC V,Sabate J A,Ridley R B,et al.Small-signal analysis of the phase-shifted PWM converter[J].IEEE Transactions on Power Electronics,1992,7(1):128-135.

[17]唐建军,梁冠安.移相全桥变换器的极点配置自适应预测控制[J].电力电子技术,2003,37(6):20-23.

Tang Jianjun,Liang Guanan.Pole-placement and adaptive digital control of phase shift bridge converter using prediction technique[J].Power Electronics,2003,37(6):20-23.

[18]张恩勤,施颂椒,高卫华,等.模糊控制系统近年来的研究与发展[J].控制理论与应用,2001,18(1):7-11.

Zhang Enqin,Shi Songjiao,Gao Weihua,et al.Recent researches and developments on fuzzy control system[J].Control Theory and Applications,2001,18(1):7-11.

[19]刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3):407- 418.

Liu Jinkun,Sun Fuchun.Research and development on theory and algorithms of sliding mode control[J].Control Theory & Applications,2007,24(3):407-418.

[20]宋立忠,陈少昌,姚琼荟.自适应离散变结构控制及其在电力系统中的应用[J].中国电机工程学报,2002,22(12):97-100.

Song Lizhong,Chen Shaochang,Yao Qionghui.Adaptive discrete variable structure control and its application to power system[J].Proceedings of the CSEE,2002,22(12):97-100.