基于有限元模型重构的多物理场耦合空心电抗器优化设计

虞振洋 王世山

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016）

0 引言

干式空心电抗器自从20 世纪80年代提出至今，以其结构简单牢固、维护方便、电感线性度好、噪声小、损耗低以及防火性能好等优点而广泛地应用于户外小电感（0.08～700mH）场合[1,2]。如何高效便捷地优化设计该类电抗器成为近年来研究的重要课题。

干式空心电抗器优化设计方法可分为解析法、数值计算辅助法和智能优化法等。其中解析法将电抗器线圈等效为同轴无限薄圆柱线圈，用聂以曼公式（Neumann Formula）和毕奥-沙伐定律（Biot-Savart Law）得到电感和磁感应强度的积分表达式，再通过Bartky 变换迭代法计算电感，再将电感代入优化公式计算，过程繁琐，人为干预较多，常用的有复合形法[3]和伸缩保差法[4]；数值计算辅助法以有限元代替解析法求解电抗器物理参数，给优化结果做校核[5,6]，只有少量文献[7]将数值计算跟优化方法结合起来；智能优化法主要是遗传算法[8]和模拟退火算法[9]，该类算法人为干预较少，具有一定的通用性，但是由于电抗器设计变量较多导致优化收敛速度较慢，甚至寻优失败，对罚函数的设置较敏感[10]；文献[11,12]将遗传算法和复合形法结合起来，提高了算法的局部搜索能力和优化效率；文献[13,14]利用有限元耦合方法分析电抗器的磁场、温度场和流体场，但是没有结合电抗器的优化。

电抗器优化设计是个多约束和多目标的问题，不同的约束条件对应不同的优化算法，也对应不同的优化目标。文献[15]分析了层等电阻电压约束对应着电抗器损耗最小，包封等温升约束对应着电抗器散热效率最大，包封等高约束对应着其结构紧凑、易于制作；文献[16]研究指出包封数大于1 干式空心电抗器不可能满足层等电阻电压、包封等温升和包封等高三个约束条件，只能在这三者间寻求平衡，但文献中没有将该方法与有限元法结合。

损耗是电抗器最重要的技术指标之一，其值的大小决定了电抗器效率的高低，对电抗器的性能有重要影响[17]。本文以层等电阻电压约束为主、层等电流密度约束为辅的优化策略，最终达到了电抗器损耗最小的目标，并使其温升差别不太大，满足设计的要求。

因此，对本文将数值计算法（有限元法）与优化设计算法结合起来，对设计变量进行预处理，降低变量的个数，将有限元模型的“重构”贯穿整个优化设计过程，充分利用了有限元法的便捷性，实现“磁场-热场-流体场”多物理场耦合分析。

1 空心电抗器有限元模型

1.1 时谐磁场边值问题及“场路”耦合

空心电抗器可以近似看作一个轴对称的旋转体，以其半径方向的一个截面为求解域，其磁场分布可以看作是一个2D 轴对称场。若各层导线两端并联加载交流电压，一般电力系统正常甚至故障工作时，系统内的位移电流可以忽略，因此其磁场可看作为准静态磁场。

对于电抗器准静态磁场，可选择矢量磁位A的环向分量为自由度（简记作为），则

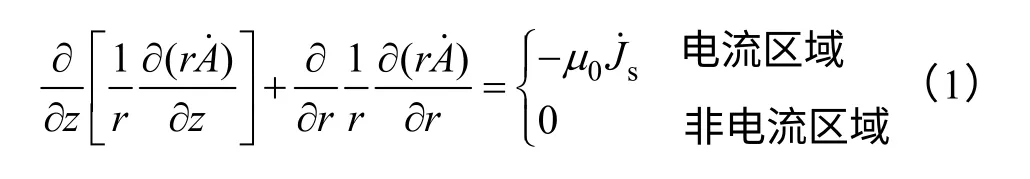
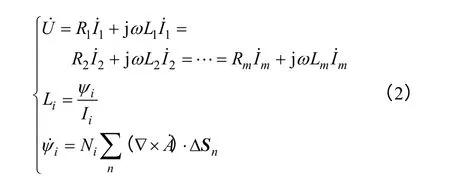
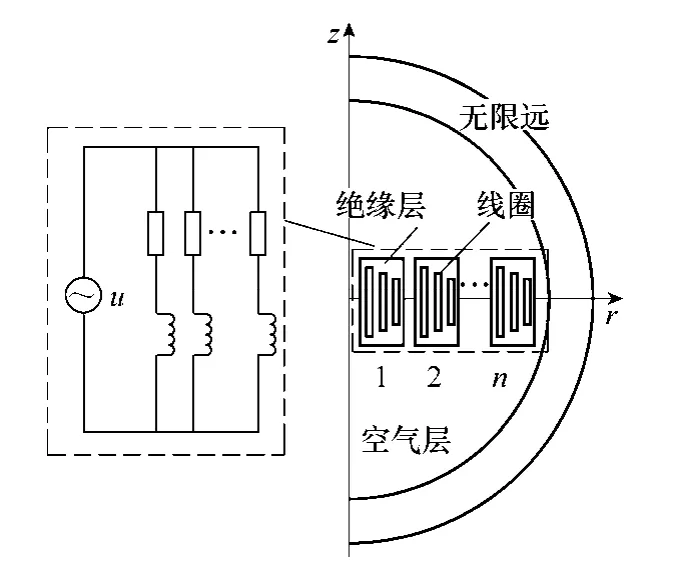
图1 空心电抗器场路耦合模型Fig.1 Coupling model of core reactor

当采用有限元法求解式（1）和式（2）时，其分界面上的边界条件、对称轴上的边界条件均可自动满足，只需设定对应的无限远标志边界和式（1）中的电流密度和式（2）中加载的电压即可。

对图1模型，结合式（1）与式（2）边值问题，在优化设计中，对每步尺寸的调整，都需要对其磁场有限元模型进行“建模→清除→再建模”的迭代过程，进而通过后处理求解出尺寸调整后的电抗器参数，通过求解的参数再对尺寸进行调整，形成一个模型重构的优化过程。

1.2 “热-流”场直接耦合边值问题

空心电抗器的热源来自每层导线的功率损耗，并通过热传导、自然对流和热辐射三种方式散热[19]。因此，其“热-流”场的求解是每个包封内以热传导传热、包封表面与周围空气以自然对流和辐射形式传热的流、固直接耦合问题。

对图1的轴对称场，对线包内热传导进行求解，其内部各点的温度T满足

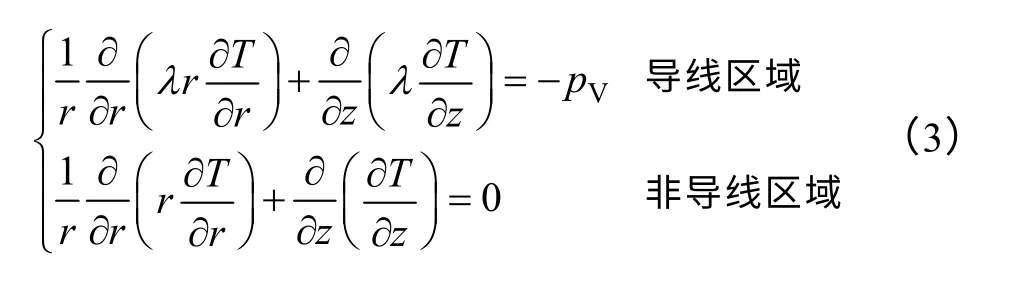
式中，λ为固体的热导率；pV为单元热功率体密度。

对于空心电抗器线圈导线，pV包含直流功率体密度pdc和涡流功率体密度pe，具体求法在第1.3 节“参数提取”中论述。

对线包表面及周围空气的热对流进行求解，其自由度满足质量、动量和能量守恒方程分别如式（4）～式（6）所示。

式中，v为空气速度矢量。

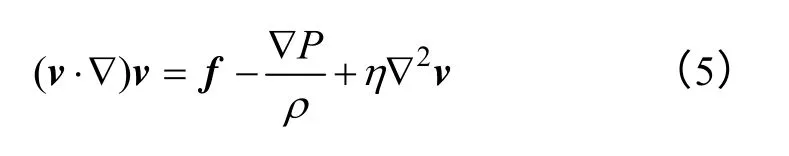
式中，ρ为空气的密度；η为空气的粘性系数；P为流体的压强；f为空气的质量力，对于空心电抗器，有径向和轴向分量。

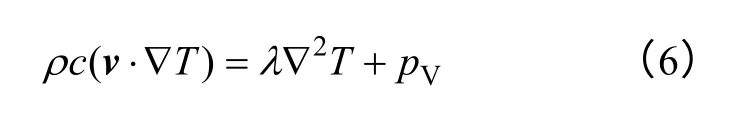
式中，c为空气的比热容。

线包表面的热辐射取决于物体表面温度，相对辐射系数和换热面积。其中，辐射系数基本恒定，在散热面积一定时，“热体”向周围空间散热总量为

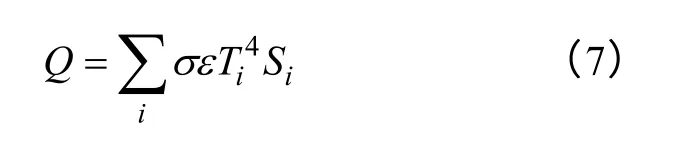
式中，σ为Stefan 常数；ε为辐射系数，对一定材料基本为常数，一般取0.8～0.9；Ti为辐射物体表面的（绝对）温度；Si为辐射部分的表面积。

对空心电抗器而言，其“热-流”场边界条件设为：对称轴上空气流速径向分量为零；各个线包表面流体速度为零；边界上空气相对压力为零，温度为环境温度。

1.3 多物理场后处理——参数提取

空心电抗器磁场求解后，后处理部分为优化设计提供所需的物理量，也是优化迭代和收敛的重要判据，这些物理量包括电流、电感、电阻和损耗等。

1.3.1 电流、电感和电阻

根据式（1）与式（2）的边值问题联合求解，得到每层线圈的电流，每层加载的电压U已知，则

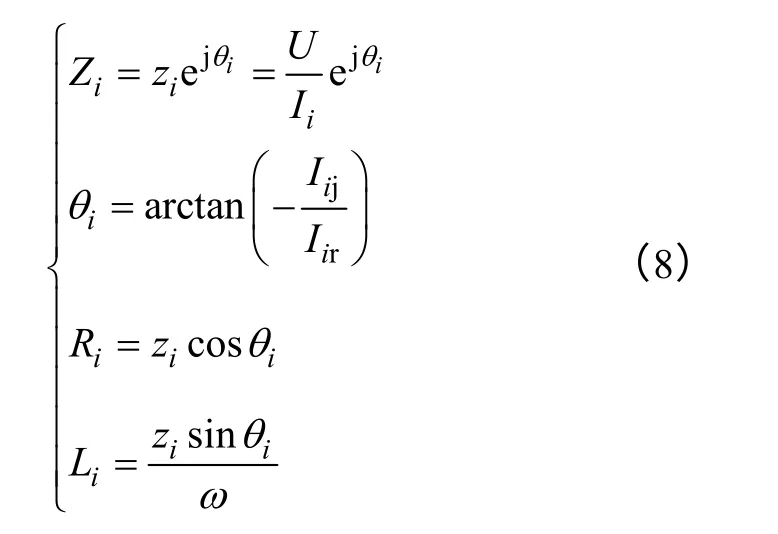
式中，Ri、Li为第i层线圈直流电阻和等效电感（解耦互感后）；θi为第i层阻抗Zi的相位角。

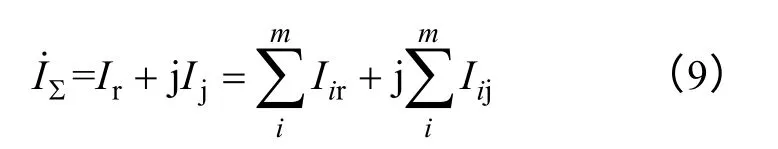
就可获得电抗器总的等效电阻R∑和等效电感L∑。

1.3.2 损耗

由于电抗器导线之间的邻近效应，其损耗分为直流损耗Pdc和交流损耗Pe。对于直流损耗则通过Pdc=I2R求得；而选择矢量磁位和电流为DOF进行“磁场-电路”耦合，不能直接求得线圈的涡流损耗，因此，本文以扁导线为例，扁导线截面示意图如图2所示，则每根导线（截面为一个剖分单元）第i个单元的交流（涡流）损耗为[20]

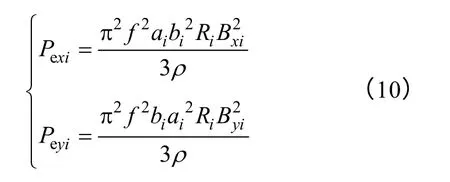
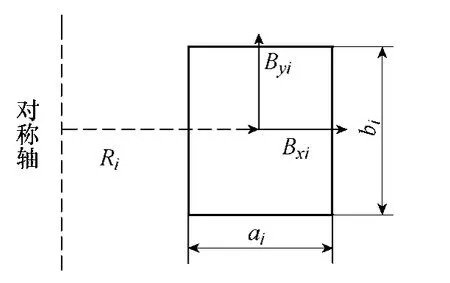
图2 扁导线截面Fig.2 Cross section of flat wire

对各匝导线涡流损耗求和得到总的交流（涡流）损耗Pe

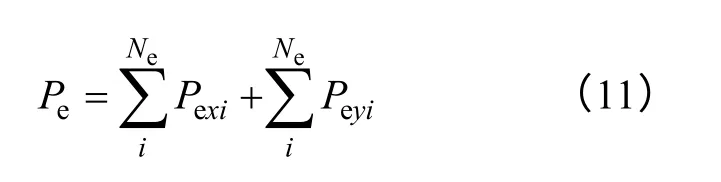
式中，Ne为导线总单元数。

1.3.3 “磁-热-流体”耦合场的对接

“磁场”与“热-流体”场属于间接耦合，两者必须保持完全一致的剖分单元和节点。计算得到的功率损耗密度代入式（3）和式（6）进行温度计算。

空心电抗器正常运行，导线温度与环境温度相差较大，造成导线电阻率发生显著增加，导致求解其功率损耗发生变化。因此，必须考虑金属导体随温度变化的因素。但是在求解前，尚不能知道导体最终的准确温度。

本文迭代首先预设导体温度Tn（矩阵，表示所有导体温度的列向量），在此基础上完成一次完整的“磁-热-流体”场耦合分析，得到导体对应温度Tn+1，若

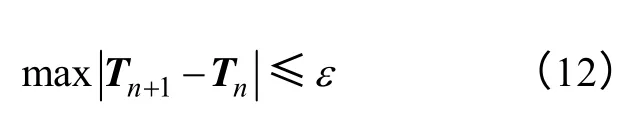
则迭代终止，Tn+1为待求温度。式中，ε为指定收敛误差。若，则令开始新一轮迭代，直到满足式（12）为止。

2 优化设计模型

干式空心电抗器优化设计是一个多变量与多约束的非线性寻优问题。为了有效快速地寻优，本文对多变量采取预处理，得到整体的设计框架并提出层等电阻电压为主、层等电流密度为辅为约束条件的双优化方案，采用邻域搜索法优化，最终达到损耗最小的优化目标。

2.1 多变量预处理

干式空心电抗器优化设计的变量包括包封数Nb，包封高度H(i)，电抗器内径D，各包封内的导线层数M(i)，导线规格C(a,b)(a×b单位mm)，每层导线匝数N(i)。

一般工程设计中，制造方会给出有限组（k组）导线规格{C(a1,b1,S1),C(a2,b2,S2),…,C(ak,bk,Sk)}（Si（i=1,2,…,k）为导线标称截面积，且S1≤S2≤…≤Sk），通过对导线标称截面积Si进行顺序遍历搜索迭代：首先假定初始总层数Nm，求出所需导线截面积S′，若S′＞Sk（Sk为最大值），则需调整Nm，再循环进行迭代，若存在一个i=l使S′≤Si，即确定合适的线规C(al,bl,Sl)及总层数Nm，如式（13）所示。

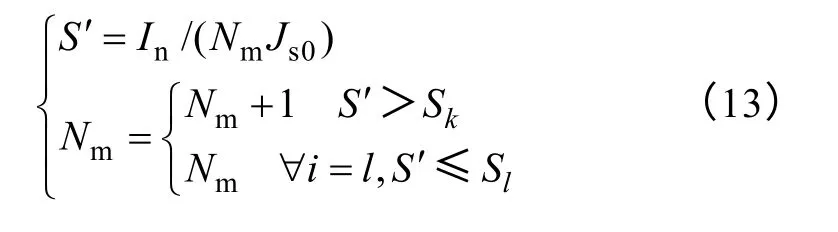
式中，In为额定电流；Js0工程设计中导线允许通入的电流密度，通常取1.0～2.5A/mm2，本文扁铝导线取1.5A/mm2。

根据工程设计经验，考虑到散热以及装配工艺，每个包封中的层数通常为3、4、5、6 层，中间的包封层数一般少于两端层数，由此在总层数的基础上确定总包封数Nb和各包封内的导线层数M(i)。

电抗器应用场合和功率大小，对长度也有限制。功率大、放置场地空旷的场合，小内径的电抗器由于散热问题不宜采用；反之，功率较小、放置场地较狭小的场合，大内径的电抗器由于耗材问题也不宜采用。为此，本文定义径高比KDH=D/H(1)，KDH越大，设计的电抗器就较扁、内径较大；KDH越小，设计的电抗器就较高、内径较小。通常情况下KDH取0.8～5.0。

在此基础上，为了加快优化收敛速度，需对每层初始匝数N0(i)进行处理。考虑到要使电抗器的结构紧凑、易于制造并节约材料，这里加入包封等高的附加约束条件。因此，每层初始匝数设为相等，即N0(i)=N0。但是，随意的N0不能加快优化收敛速度，本文以使得电抗器的总电流I等于额定电流In为约束条件，通过对匝数N0反复迭代来确定初始匝数N0。

毫无疑问，总电流和匝数之间存在一定的相关关系。理想状况下，由于空心电抗器每层线圈是并联关系，其总电感可以近似看成线圈匝数为N0单层并绕电抗器的电感，则有

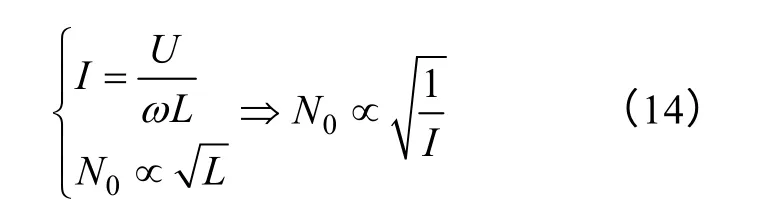
式中，总电流I需通过磁场求解提取出，而匝数的迭代过程需要在有限元模型进行重构迭代中完成。具体过程如下：

（1）设定初始匝数N0。

（2）建立有限元模型，求解磁场。根据式（9）求出总电流I∑。

（4）确定合适的初始匝数N0。

确定了合适的初始匝数，空心电抗器优化设计的框架也就确定了，多变量转化为单变量（每层匝数N(i)），后续的优化则是对单独每层匝数N(i)进行微调以达到设计目标。

2.2 主、辅双约束优化方案

本文以电抗器损耗最小为设计目标。文献[7]经过推导得到当电抗器各个包封的电阻电压相等时，电抗器损耗最小，即

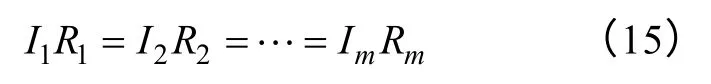
令Vi=RiIi，对每一层线圈，有Ri∝N(i)，根据式（14），得知Ii∝1/N2(i)。综上所述，Vi在其N(i)的一个邻域内近似有Vi∝1/N(i)，因此适当地调整每层匝数N(i)就可以让V(i)满足约束条件。匝数调整的具体迭代算子为

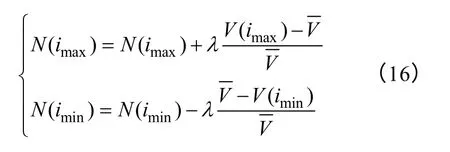
收敛判据为

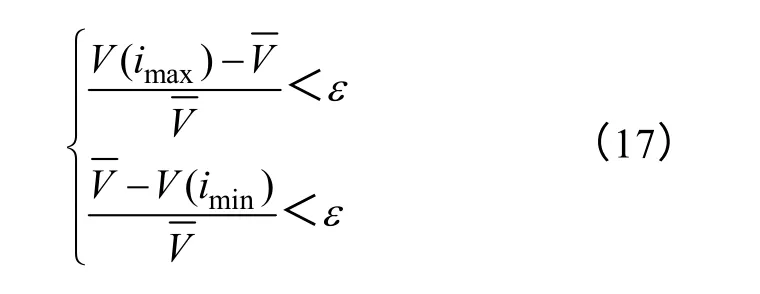
式中，ε为收敛误差。

整个迭代过程同样基于有限元模型重构后磁场分析的参数提取。为了防止各层导线电流密度差别太大，使得部分线包过热，还需进行层等电流密度的优化。其约束条件为

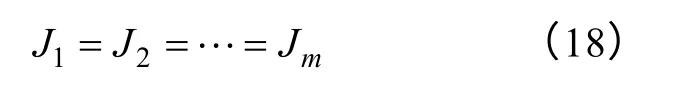
式中，电流密度Ji=Ii/S，S为导线截面积。

由于导线规格已定，根据式（14），则Ji∝ 1/N2(t)。因此，层等电流密度的优化过程和层等电阻电压的优化相似，其迭代算子为

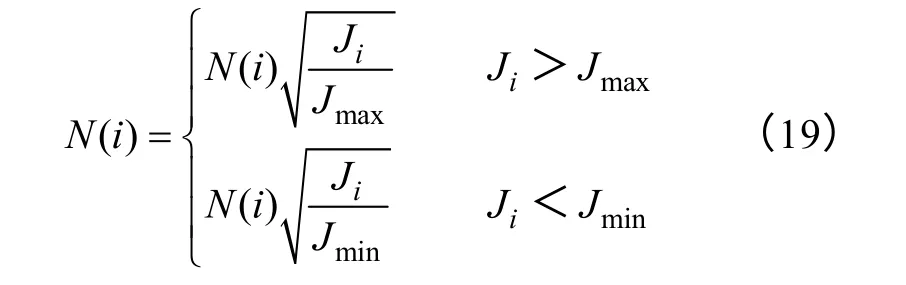
式中，Jmax、Jmin分别为线圈导线设定的最大、最小的电流密度值。这样每层线圈电流密度就不会太大而过热，也不会太小而使得材料利用率不高。

收敛判据为

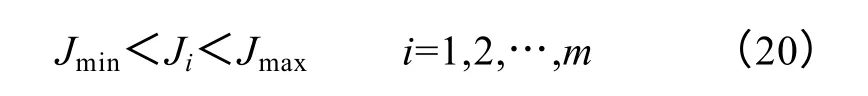
以上优化方法的实施是以层等电阻电压约束为主优化方向、层等电流密度为辅助优化方向，因此前者收敛判据较后者更为严格。

3 优化设计实例

3.1 设计指标

根据制造方的要求，本文以两个干式空心电抗器为例，采用基于有限元模型重构的多物理场耦合的优化设计方法进行优化设计，其设计指标见表1。

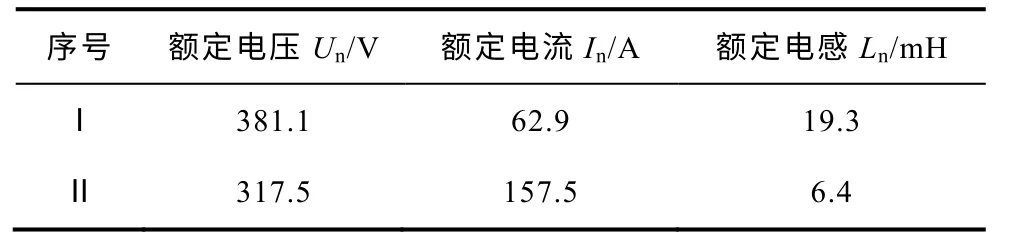
表1 设计要求指标Tab.1 The required design indexes

考虑到绕制工艺的简便和导线载流量高的要求，本文采用扁铝导线，其一系列的规格见表2。

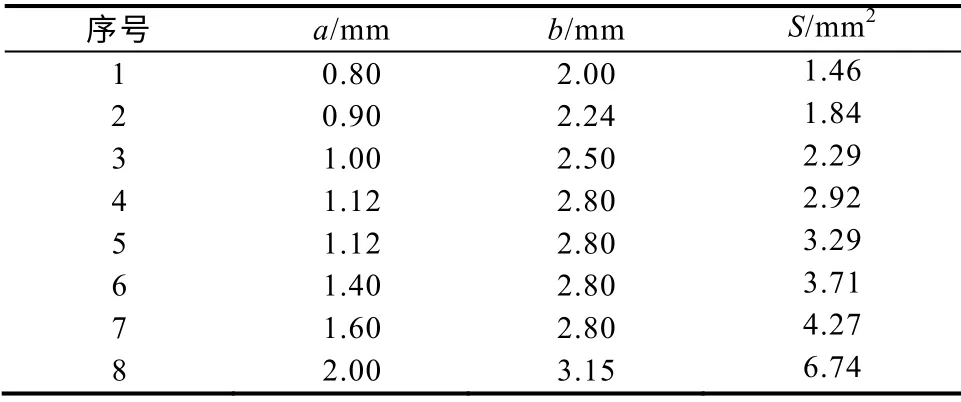
表2 导线规格Tab.2 The wire gauge

3.2 设计变量的预处理

对电抗器优化设计的变量进行预处理，选取导线规格、确定线包总层数、线包个数以及初始匝数，预处理结果见表3。

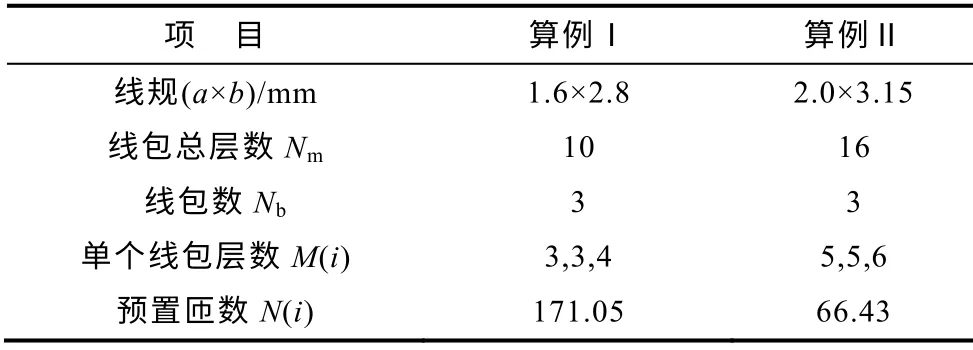
表3 设计变量预处理Tab.3 Preprocessing of design variables

对初始匝数进行选取，其迭代收敛误差设为10%，收敛过程如图3所示。从图3可知，迭代次数为7 次，该算法的收敛速度较快。

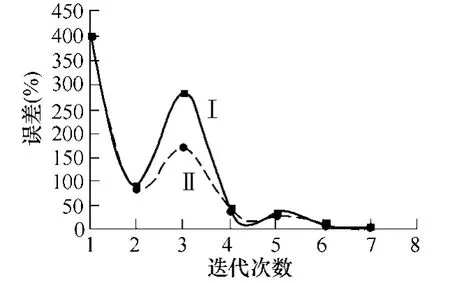
图3 初始匝数预置的收敛过程Fig.3 Convergence process of preset initial turns

3.3 优化设计结果及分析

对设计变量预处理而确定的电抗器设计整体框 架进行匝数调整，来满足以层等电阻电压为主、层等电流密度为辅的约束条件，最终达到损耗最小的目标。其中主、辅双优化迭代误差如图4所示，收敛误差为10%。

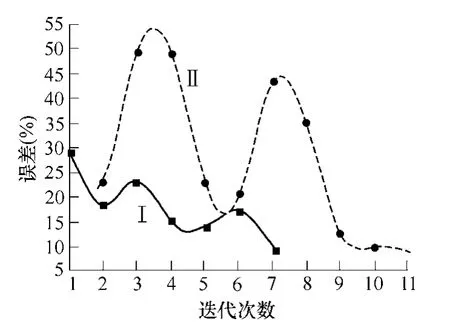
图4 基于主、辅双约束的优化收敛过程Fig.4 Optimized convergence process based on the main and auxiliary constraint

图4中，两个设计算例分别迭代7 次和11 次达到收敛点，可见，对于总层数较多的电抗器，迭代次数较多，优化时间较长。

通过软件计算，得到空心电抗器优化设计结果，其各项指标见表4，设计清单见表5。

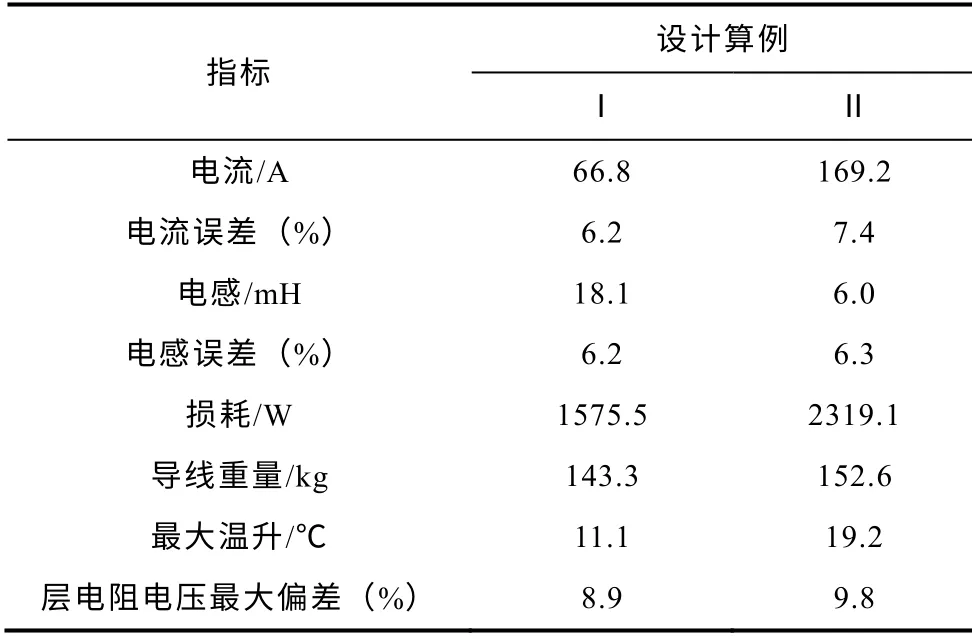
表4 设计指标Fig.4 The design indexes

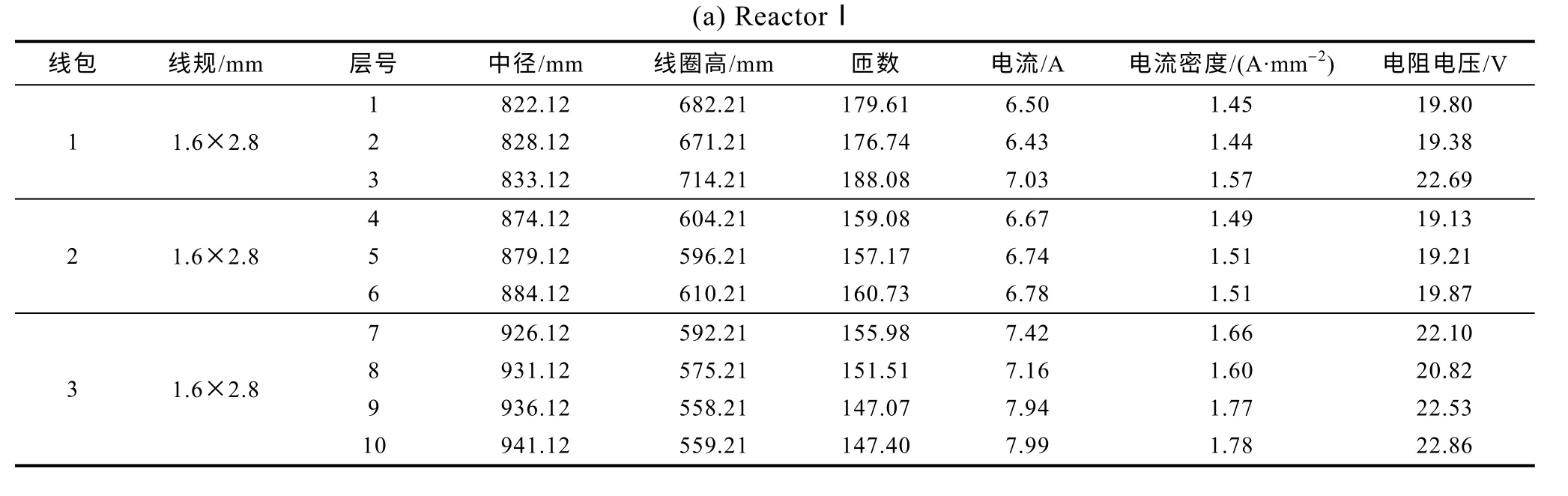
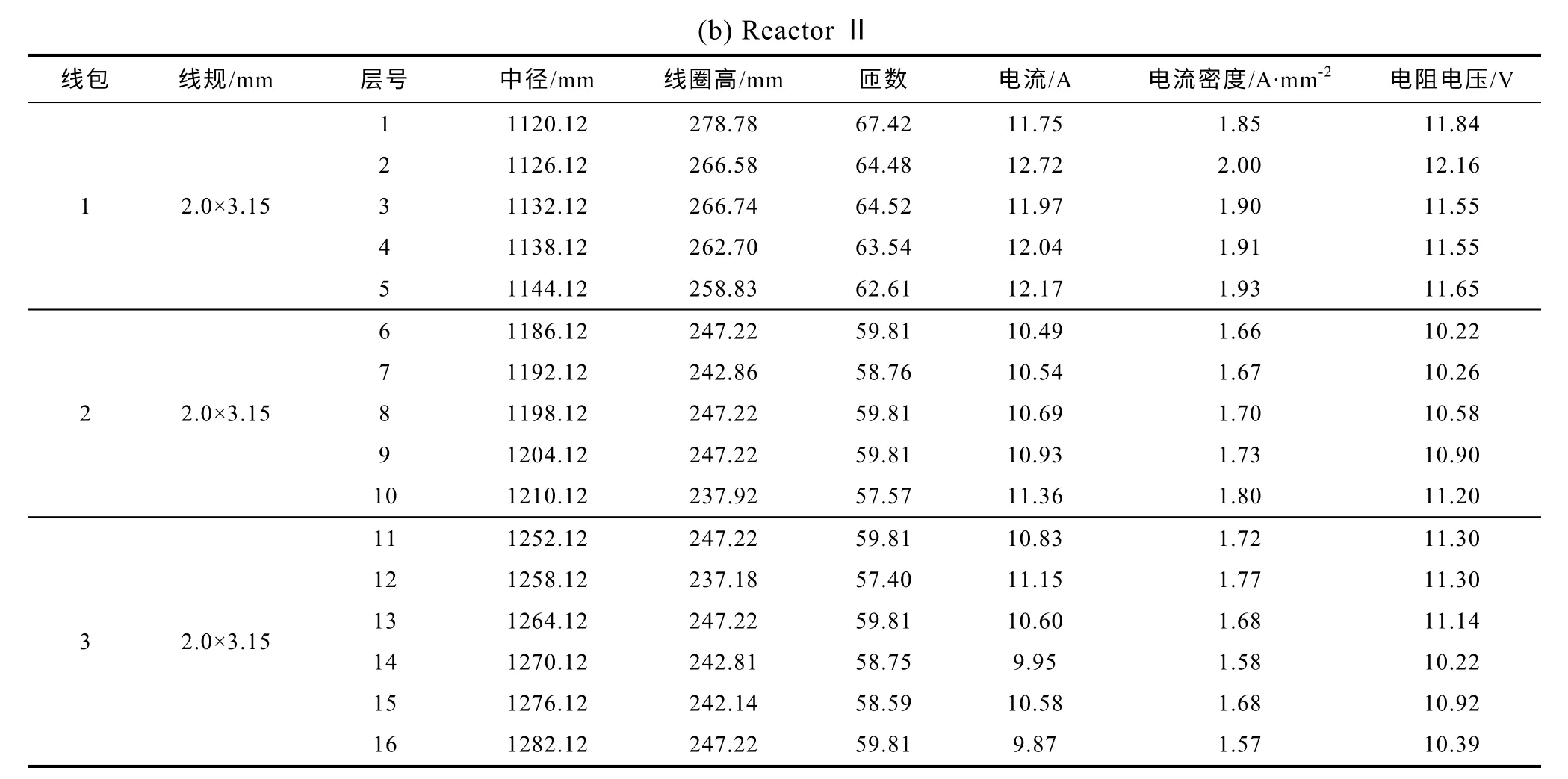
表5 优化设计清单Tab.5 Calculation list of Pareto optimal design result

(b)Reactor Ⅱ 线包 线规/mm 层号 中径/mm 线圈高/mm 匝数 电流/A 电流密度/A·mm-2电阻电压/V 1 2.0×3.15 1 1120.12 278.78 67.42 11.75 1.85 11.84 2 1126.12 266.58 64.48 12.72 2.00 12.16 3 1132.12 266.74 64.52 11.97 1.90 11.55 4 1138.12 262.70 63.54 12.04 1.91 11.55 5 1144.12 258.83 62.61 12.17 1.93 11.65 2 2.0×3.15 6 1186.12 247.22 59.81 10.49 1.66 10.22 7 1192.12 242.86 58.76 10.54 1.67 10.26 8 1198.12 247.22 59.81 10.69 1.70 10.58 9 1204.12 247.22 59.81 10.93 1.73 10.90 10 1210.12 237.92 57.57 11.36 1.80 11.20 3 2.0×3.15 11 1252.12 247.22 59.81 10.83 1.72 11.30 12 1258.12 237.18 57.40 11.15 1.77 11.30 13 1264.12 247.22 59.81 10.60 1.68 11.14 14 1270.12 242.81 58.75 9.95 1.58 10.22 15 1276.12 242.14 58.59 10.58 1.68 10.92 16 1282.12 247.22 59.81 9.87 1.57 10.39

由表4 和表5 看出，本文设计优化的空心电抗器各项参数误差在10%以内，满足设计要求。

4 结论

本文以干式空心电抗器为研究对象，采用有限元法对其建立多物理场模型并对其中的电磁场模型进行“建模-清除-再建模”的迭代，提出了以层等电阻电压为主、层等电流密度为辅的双优化方案，达到损耗最小的优化目标，并以设计实例进行验证，得到以下结论：

（1）提出了一种基于有限元磁场参数提取的干式空心电抗器设计优化初始条件的设定方法。由额定电流、规定导线电流密度及规定线规确定电抗器的层数，进而确定线包数；由求解有限元磁场模型得到的电抗器总电流和额定电流相等，确定初始 匝数。

（2）提出一种基于有限元模型重构的改进型邻域搜索寻优法，对匝数进行微调，利用有限元求解出电感、电流和电阻等参数，省去繁琐的公式调用，最终使各层电流密度在约束范围内、各层电阻电压相等，从而达到损耗最小的优化目标。

（3）采用有限元建立干式空心电抗器的多物理场模型，并对其中电磁场模型进行“建模-清除-再建模”的迭代，对每次迭代结果提取参数进行优化计算，具有较高的准确性，电磁参数优化结束后即对热流场计算结果进行性能校核，缩短了设计周期，降低了试验成本。并且这种优化设计思路可以拓展应用到其他电力设备结构优化中，具有普遍性。

[1]路长柏.电抗器理论与计算[M].沈阳:沈阳出版社,2009.

[2]李霞,刘燕,肖勋.关于干式空心电抗器试验的几个问题[J].变压器,2013,50(2):57-59.

Li Xia,Liu Yan,Xiao Xun.Several questions of dry-type air-core reactors test[J].Transformer,2013,50(2):57-59.

[3]夏天伟,闫英敏.干式空心限流电抗器的优化设计问题[J].电机与控制学报,1998,2(1):51-53.

Xia Tianwei,Yan Yingmin.Optimum design of dry- type air-core current-limited reactor[J].Electric Machines and Control,1998,2(1):51-53.

[4]曹云东,夏天伟,高慧萍,等.干式空心电抗器优化设计中等式约束处理的研究[J]．电工技术学报,1999,14(4):31-34.

Cao Yundong,Xia Tianwei,Gao Huiping,et al.Research of the equality constraints in the optimum design of the dry-type air reactors[J].Transactions of China Electrotechnical Society,1999,14(4):31-34.

[5]Yan Xiuke,Dai Zhongbin,Zhang Yanli,et al.Fluid- thermal field coupled analysis of air core power reactor[C].Electromagnetic Field Problems and App- lications(ICEF),2012:1-4.

[6]刘志刚,王建华,耿英三,等.干式空心电抗器设计软件开发与应用[J].电机与控制学报,2003,7(2):103-106.

Liu Zhigang,Wang Jianhua,Geng Yingsan,et al.Development and application of design software of dry-type air-core reactor[J].Electric Machines and Control,2003,7(2):103-106.

[7]刘志刚,耿英三,王建华,等.干式空心电抗器的优化设计[J].高电压技术,2003,7(2):103-106.

Liu Zhigang,Geng Yingsan,Wang Jianhua,et al.The optimum design of dry-type air-core reactor[J].High Voltage Engineering,2003,7(2):103-106.

[8]刘志刚,耿英三,王建华,等.基于改进自适应遗传算法的空心串联电抗器优化设计[J].中国电机工程学报,2003,23(9):103-106.

Liu Zhigang,Geng Yingsan,Wang Jianhua,et al.Optimum design of dry-type air-core series reactor based on modified adaptive genetic algorithm[J].Proceedings of the CSEE,2003,23(9):103-106.

[9]刘志刚,王建华,耿英三,等.一种改进的遗传模拟退火算法及其应用[J].系统仿真学报,2004,16(5):1099-1101.

Liu Zhigang,Wang Jianhua,Geng Yingsan,et al.A modified genetic simulated annealing algorithm and its application[J].Journal of System Simulation,2004,16(5):1099-1101.

[10]刘志刚,欧阳森,耿英三,等.遗传算法在空心电抗器优化设计中的应用研究[J].电工电能新技术,2003,22(3):45-49.

Liu Zhigang,Ouyang Sen,Geng Yingsan,et al.Study of genetic algorithm in the optimum design of air-core reactor[J].Advanced Thechnology of Electrical Enginee- ring and Energy,2003,22(3):45-49.

[11]Zhao Y,Chen F,Kang B,et al.Optimum design of dry-type air-core reactor based on the additional constraints balance and hybrid genetic algorithm[J].International Journal of Applied Electromagnetics and Mechanics,2010,33(1):279-284.

[12]康博.干式空心电抗器的优化模型与混合遗传算法优化设计[D].西安:西安交通大学,2009.

[13]刘志刚,耿英三,王建华,等.基于流场-温度场耦合计算的新型空心电抗器设计与分析[J].电工技术学报,2003,18(6):59-63.

Liu Zhigang,Geng Yingsan,Wang Jianhua,et al.Design and analysis of new type air-core reactor based on coupled fluid-thermal field calculation[J].Transactions of China Electrotechnical Society,2003,18(6):59-63.

[14]刘志刚,王建华,耿英三,等.基于耦合方法的干式空心阻尼电抗器温度场计算[J].西安交通大学学报,2003,37(6):622-625.

Liu Zhigang,Wang Jianhua,Geng Yingsan,et al.Calculation of temperature field of dry-type air-core damping reactor based on coupled method[J].Journal of Xi'an Jiaotong University,2003,37(6):622-625.

[15]刘全峰,党红阁,梁艺超,等.电抗器设计优化算法[J].电力电容器与无功补偿,2011,32(5):46-50.

Liu Quanfeng,Dang Hongge,Liang Yichao,et al.Optimization algorithm of the reactor design[J].Power Capacitor & Reactive Power Compensation,2011,32(5):46-50.

[16]赵彦珍,康博,马西奎.基于附加约束条件平衡原则的干式空心电抗器优化模型[J].电工技术学报,2010,25(11):80-83.

Zhao Yanzhen,Kang Bo,Ma Xikui.Optimization model of dry type air-core reactor based on balance of additional constraints[J].Transactions of China Elec- trotechnical Society,2010,25(11):80-83.

[17]Sippola M,Sepponen R E.Accurate prediction of high-frequency power-transformer losses and tem- perature rise[J].IEEE Transactions on Power Elec- tronics,2002,17:835-847.

[18]颜威利,杨庆新,汪友华,等.电气工程电磁场数值分析[M].北京:机械工业出版社,2005.

[19]Ortiz C,Skorek A W,Lavoie M,et al.Parallel CFD analysis of conjugate heat transfer in dry-type trans- former[J].IEEE Transactions on Industry Applications,2009,45(4):1503-1504.

[20]Boglietti A,Lazzari M,Pastorelli M.A simplified method for the iron losses prediction in soft magnetic materials with arbitrary voltage supply[A].IEEE Piscataway,USA,2000:269-276.