新型铁钻工铰接臂铰点位置的优化
占自涛,沙永柏,王清岩,朴冲,刘晓利
(1.吉林大学机械科学与工程学院,吉林长春130025;2.吉林大学建设工程学院,吉林长春130026)
新型铁钻工铰接臂铰点位置的优化
占自涛1,沙永柏1,王清岩2,朴冲1,刘晓利1
(1.吉林大学机械科学与工程学院,吉林长春130025;2.吉林大学建设工程学院,吉林长春130026)
鉴于铁钻工铰接臂铰点的位置直接影响伸展与升降油缸的最大工作压力与油压稳定性,在分析铁钻工铰接臂运动特性的基础上,以降低最大工作压力与提高压力稳定性为目标,采用统一目标函数法建立针对铰点位置的优化模型。采用遗传基因算法,利用Matlab优化工具箱,优化铰点位置。根据优化结果,借助Adams软件建立铰接臂动力学模型,比较优化前后伸展与升降油缸油压的变化情况。仿真结果表明:优化后的铰点位置大大提高铰接臂工作性能。
铁钻工;铰接臂;铰点位置优化;最大工作压力;油压稳定性;遗传基因算法;动力学分析
铁钻工是一种多功能、安全高效的钻具旋扣设备,主要完成钻井作业中上卸钻杆接头丝扣、正常钻进时卸方钻杆接头、上卸钻挺、甩钻杆、活动井下工具等工作。开展针对铁钻工的研发,推广现代设计的理论方法,对加快推进我国石油机械的现代化与自动化,有重要意义。在借鉴国内外对铁钻工研究设计有益经验[1⁃3]的基础上,吉林大学深部探测装备研制课题组开展了对铁钻工的研发,取得了一系列的成果[4⁃5]。
铁钻工铰接臂主要连接支撑总成与钳体[6],实现带动钳体快速、平稳的对准钻杆接头处的作用。铰接臂是铁钻工的关键部件之一,其设计水平直接影响铁钻工工作性能。铰接臂铰点位置的确定与伸伸展与升降油缸的最大工作压力与压力稳定性直接相关,进而决定铁钻工整机的工作效率与经济性指标。因此,针对铰接臂铰点位置的优化,在铁钻工的研发过程越来越受到重视。
传统上,对铁钻工铰接臂的设计与优化均以图解法为主。随着现代设计理论方法的普及,特别是遗传算法、正交设计,蚁群算法等智能算法的出现,为机构铰点优化提供了新的手段。
本文在对铰接臂进行运动与受力分析的基础上,运用现代设计理论,建立对铰点位置的优化模型,并利用Matlab遗传算法优化工具箱对铰接臂铰点位置进行优化。在此基础上,建立动力学模型验证优化效果。
1 铰接臂运动与受力分析
图1为新型铁钻工数字样机三维模型图。铰接臂主要由伸展油缸、升降油缸、上连杆、下连杆、支撑杆、上滑车、下滑车等组成,其结构简图如图2所示。该结构具有结构紧凑、自重轻、工作平稳的优点。参照图2,以伸展运动为例分析,∠FCD为驱动变量,伸展油缸4行程变化,油缸8行程保持不变,整体机构变为单自由度问题。

图1 SP⁃I⁃04铁钻工数字样机图Fig.1 The digital prototype of the SP⁃I⁃04⁃type iron roughneck
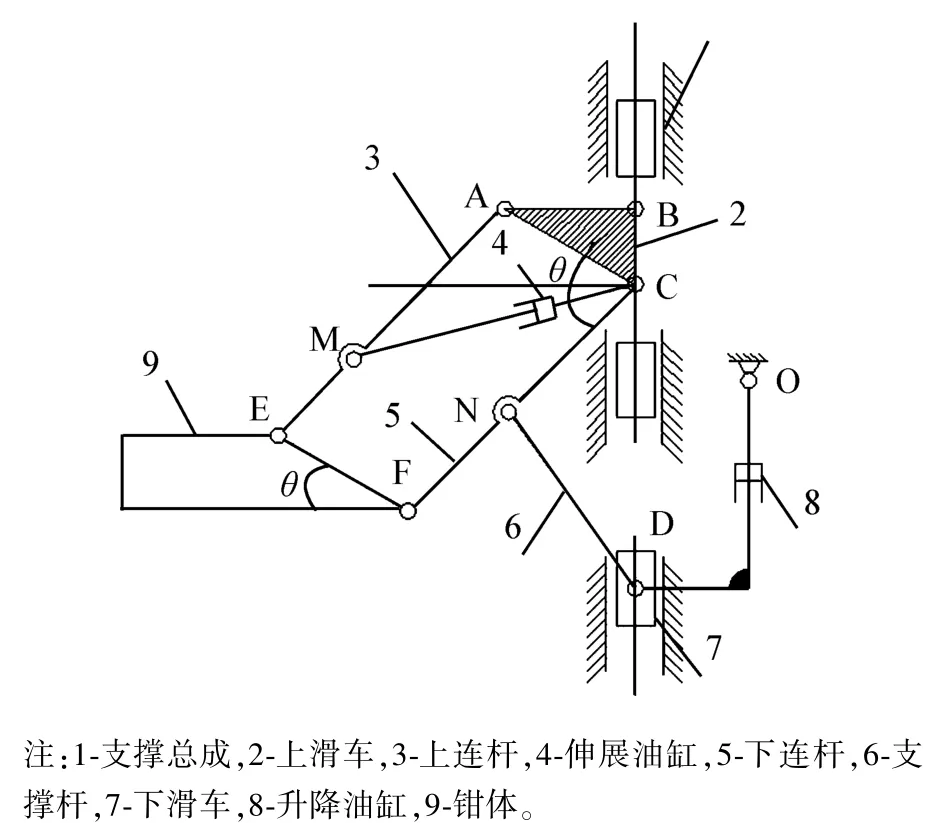
图2 铁钻工铰接臂结构简图Fig.2 The structure diagram of articulated boom
根据图2所示的几何关系

对A、C点分别取矩,则有

由于连杆质量相对于油缸作用力以及E、F、M、N点的受力很小,此处忽略不计连杆重力。
伸展油缸对A点的作用力臂
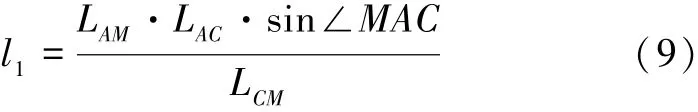
二力杆ND对C点作用力臂

Fex、Fey、Ffx、Ffy分别为E、F 2点在横轴与纵轴上的受力,F1、F2分别为伸展油缸与升降油缸的作用力。对钳体9受力分析可知

式中:G是钳体质量。
联立(7)~(11),求得

需要说明的是,由于伸展动作较缓慢,所以此处对钳体质量引起的惯性力忽略不计。联立(4)、(5)、(9)、(12)此处,记伸展油缸传力比[7]

根据伸展油缸与升降油缸传力比的计算式(13)、(14),其表达式含有较复杂的非线性函数。为减小油缸的最大工作压力和提高油压稳定性,需要以伸展油缸与升降油缸的传力比的计算式为依据进行优化。上述优化的关键是要合理布局铰点M、N位置以及选定拉杆DN长度与拉杆AC的水平夹角θ。
2 优化模型
2.1 目标函数的建立
在确保铁钻工铰接臂伸展动作平稳的基础上,结合动力学以及经济性的要求,本文选定伸展油缸与升降油缸的最大工作压力最小和压力稳定性最好为优化的目标函数,依据计算式(12),上述的要求可转化为最小传力比最大以及伸展过程中传力比的变化量最小。
2.1.1 最大工作压力为目标函数
为了使铁钻工铰接臂在举升钳体的过程中,达到以较小的油缸输入力输出尽可能大的作用力的目标,需要优化结构尺寸。所以当该目标在外部载荷近似恒定的前提下,可通过结构尺寸的优化,实现油缸输出力的最小化。即在伸展角度∠FCD范围确定的情况下,使传力比le1、le2的最小值最大作为目标函数,达到油缸作用力F1、F2的最大值最小。为统一形式,根据伸展油缸与升降油缸的传力比公式,分别选择其倒数作为目标函数,进而分别取其最小值。
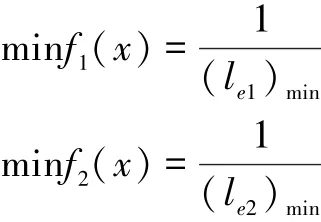
2.1.2 油压稳定性为目标函数
为了保护液压元件,避免出现出现较大的油压波动,需要提高油缸压力的稳定性,即要求伸展与升降油缸的油压在整个伸展动作的过程中变化量最小。本文中,在伸展角度∠FCD变化范围内,根据最大压力差可以推算出伸展与升降油缸油压的变化值为[7]
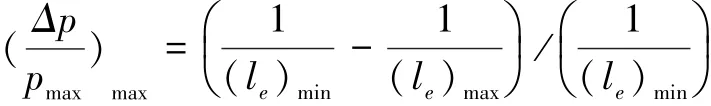
统一形式,分别对伸展油缸与升降油缸的油压稳定性选定以下的优化目标函数

式中:(le1)min、(le1)max、(le2)min、(le2)max分别是随∠FCD变化时,伸展油缸的最大传力比和最小传力比、升降油缸的最大传力比和最小传力比。
采用统一目标函数线性加权和法求解上述四目标函数优化问题,即本文优化的综合目标函数为minF x()=ω1·f1x()+ω2·f2x()+ω3·f3x()+ω4· f4x(),根据各子目标函数对机构性能影响的重要程度[7⁃8],分配权重因子ω1、ω2、ω3、ω4,得到最终优化的目标函数
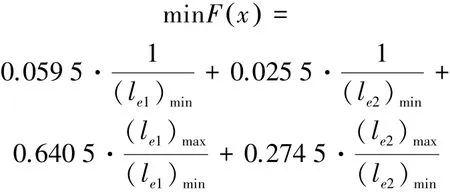
2.2 设计变量的确定
为保证铁钻工铰接臂实现举升运动,以∠FCD为驱动量,为节省钻井平台空间以及避免杆件干涉,取1°≤∠FCD≤3°,为确保最大伸展范围与举升高度,取70°≤∠FCD≤75°。确定∠FCD后,根据伸展与升降油缸的传力比公式,设定优化模型的设计变量的向量表达式:
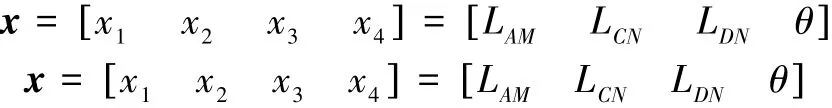
2.3 优化的约束条件
2.3.1 边界条件
为缩小寻优范围,考虑初始的设计尺寸,根据经验可适当的设置设计变量的上下限。据此,建立了8个边界约束条件:
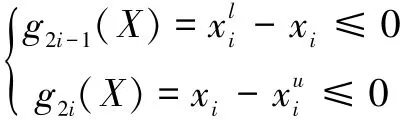
2.3.2 运动的约束
在保证ΔAMC、ΔCND互容性的基础上,根据机构设计避免出现死点的要求[9],两油缸的传动角需在[40°,140°],则有
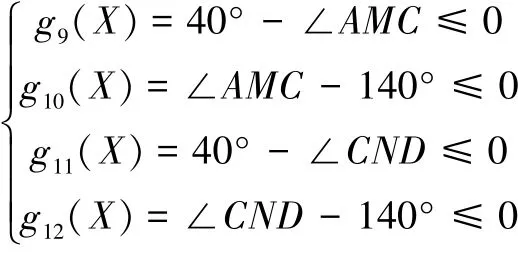
根据油缸稳定性的要求[9],需要对油缸的伸缩比加以约束,则有g13(X)=λmax=(LCM)max/(LCM)min-1.7≤0。
2.4 优化结果
根据SP⁃I⁃04型铁钻工铰接臂的设计尺寸,结合实际工况的要求,给定以下的优化参数,取∠FCDmin=1.5°,∠FCDmax=70°,G=36 003 N,LAC=394 mm,LAC= 2 030 mm,其他设计变量及可行域见表1。上述初值是参考国内外同类型较成熟的设计数据确定,可行域是按照单变量变化以及设计经验给定。
选择遗传算法的种群大小为120,编码方式为格雷码混合编码,选择操作采用轮盘赌转轮法,单点交叉,交叉率Pc=0.4,变异率Pm=0.03,进化代数N=69,α=0.995,繁殖数σ=5,繁殖率μ=0.85。
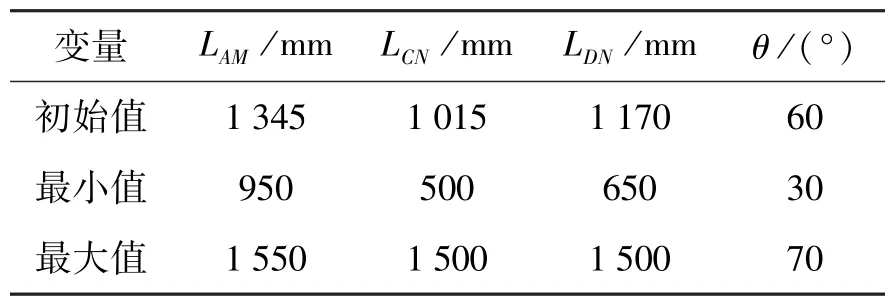
表1 SP⁃I⁃04铁钻工铰接臂优化的设计变量的初值Table1 The relative position of the parameters and the feasible region of articulated boom for SP⁃I⁃04⁃type tron roughneck
利用Matlab优化工具箱,对上述优化模型进行优化运算,得到如表2所示的优化结果。

表2 铰接臂设计变量优化结果Table2 The optimal result of design variables
3 仿真验证及动力学分析
为检验上述优化结果所达到的效果,建立如图3所示的铁钻工铰接臂的动力学模型。在上述模型中,得到优化前后伸展油缸与升降油缸的受力随驱动量∠FCD的变化关系。结合油缸的内径以及活塞杆直径等参数以及油缸布置方式,将上述关系分别转化为伸展油缸油压与∠FCD的变化关系,如图4所示;升降油缸油压与∠FCD的变化关系,如图5所示。
从图4可知,相对于初始设计值,优化后的伸展油缸的最大工作压力降低了8.4%,油压稳定性提高了13%;伸展油缸完成伸展动作的平均工作压力降低了25%~30%。分析表明铰接臂铰点位置的优化改善了伸展油缸的工作特性。
图3 铁钻工铰接臂的动力学模型Fig.3 The dynamic model of articulated boom for SP⁃I⁃04⁃type iron roughneck
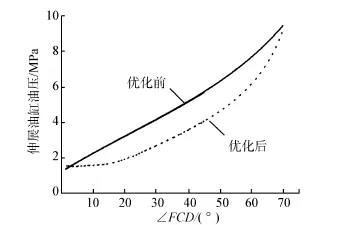
图4 伸展油缸油压与∠FCD的变化关系Fig.4 The value of load changes of the stretching cylin⁃der vs.∠FCD,before and after optimization
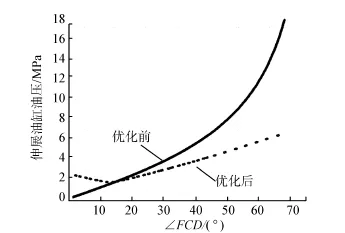
图5 升降油缸油压与∠FCD的变化关系Fig.5 The value of load changes of the lifting cylinder vs.∠FCD,before and after optimization
从图5可知,相对于初始设计值,优化后的升降油缸最大工作油压降低了62.8%,油压稳定性提高了78%,升降油缸完成伸展动作的平均工作压力下降了30%~35%左右。分析表明铰接臂铰点位置的优化大大地改善了升降油缸的工作特性。
此外,图4与图5中,在伸展角度∠FCD较大值处,优化后的伸展油缸与升降油缸的承载效果明显改善,油缸的最大压力值控制在合理范围,且油压波动较小,稳定性较好,可有效避免了液压冲击,这对铁钻工钳体完成上卸扣作业很有好处,改善了铰接臂的工作性能。
4 结论
1)通过对铁钻工铰接臂运动特性的分析,利用统一多目标函数法建立针对铰接臂铰点位置优化的数学模型。
2)利用Matlab优化工具箱,采用遗传基因算法,求解优化模型,得到关于铰点位置的优化结果。
3)根据优化结果,建立铰接臂的动力学模型,对比优化前后伸展油缸与升降油缸油压最大值与油压波动,验证了优化效果,达到了改善铰接臂工作特性的要求。
4)上述优化结果为铁钻工铰接臂的设计提供了理论依据;优化的流程为类似机构铰点优化提供了新的思路。
[1]于昊.TZG216⁃110型铁钻工的机构研究[D].兰州:兰州理工大学,2008:38⁃42.
YU Hao.The structure research of TZG216⁃110⁃type iron roughneck[D].Lanzhou:Lanzhou University of Technology,2008:38⁃42.
[2]MASON D B.Iron roughneck.United States Patent.US 6776070 B1[P].2004⁃08⁃17.
[3]BELIK J.Automated arm for position of drilling tools such as an iron roughneck[P].United states patent.US 7249639 B2.2007⁃06⁃30.
[4]孙友宏,吕兰,沙永柏,等.一种铁钻工[P].中国专利,103132931A,2013⁃06⁃05.
[5]孙友宏,吕兰,王清岩,等.一种铁钻工回转及平移伸展机构[P].中国专利,103114817A,2013⁃05⁃22.
[6]谷敏永.TZG216⁃110型铁钻工铰接臂优化设计研究[D].兰州:兰州理工大学,2010:19⁃20.
GU Minyong.Optimization research of articulated boom for TZG216⁃110⁃type iron roughneck[D].Lanzhou:Lanzhou U⁃niversity of Technology,2010:19⁃20.
[7]何清华,朱俊霖,王石林,等.伸缩臂叉装车变幅机构的铰点位置优化[J].华中科技大学学报,2011,11(39):423⁃429.
HE Qinghua,ZHU Junlin,WANG Shilin,et al.The optimi⁃zation of the hinge point position of leveling mechanism for telescopic handler[J].Journal of Huazhong University of Science and Technology,2011,11(39):423⁃429.
[8]马成业,黎锁平,杨胜良.模糊多目标可靠性优化设计的遗传算法[J].兰州理工大学学报,2009,2(35):156⁃158.
MA Chengye,LI Suoping,YANG Shengliang.Genetic algo⁃rithm for fuzzy multi⁃objective optimization of reliability[J].Journal of Lanzhou University of Technology,2009,2(35):156⁃158.
[9]成大先.机械设计手册[M].4版.北京:化学工业出版社,2004:4⁃55,17⁃258.
Optimization of the hinge point position of the articulated boom for SP⁃I⁃04⁃Type iron roughneck
ZHAN Zitao1,SHA Yongbai1,WANG Qingyan2,PIAO Chong1,LIU Xiaoli1
(1.College of Mechanical Science and Engineering,Jilin University,Changchun 130025,China;2.College of Construction Engineer⁃ing,Jilin University,Changchun 130026,China)
The hinge point position of the articulated boom of an iron roughneck is a key factor that directly affects the maximum working pressure and the hydraulic pressure stability of the stretching cylinders and the lifting cylin⁃ders.Therefore,based on the analysis of the motion characteristics of the articulated boom,a mathematical model aiming at the optimization of the hinge point position is built with unified objective function method,which regards reduction of the maximum working pressure and enhancement of the pressure stability as the optimization objective.Using the genetic algorithm and the optimization toolbox of Matlab,the optimized position of the hinge point is pres⁃ented.Furthermore,according to the optimization result above,a dynamic model for the articulated boom is estab⁃lished by Adams software,to compare the changes of working pressure value of the stretching cylinders and the lift⁃ing cylinders before and after optimization.The simulation results indicate that optimization of the hinge point posi⁃tion greatly improves the performance of the articulated arm.
articulated boom;iron roughneck;optimization of the hinge point position;maximum working pressure;pressure stability;genetic algorithm;dynamic analysis
10.3969/j.issn.1006⁃7043.201306004
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006⁃7043.201306004.html
TH460.20
A
1006⁃7043(2015)02⁃0205⁃04
2013⁃06⁃03.网络出版时间:2014⁃11⁃27.
国家深部探测技术与实验研究专项资助项目(SinoProbe⁃09⁃05).
占自涛(1989⁃),男,硕士研究生;王清岩(1970⁃),教授,硕士生导师.
王清岩,E⁃mail:wangqy@jlu.edu.cn.

