基于相位差变化率单站无源定位及其试验方法研究

张政超，李文臣，袁翔宇，陈 杨，李 宏

基于相位差变化率单站无源定位及其试验方法研究

张政超，李文臣，袁翔宇，陈 杨，李 宏

（中国洛阳电子装备试验中心，洛阳 471003）

在建立基于相位差变化率的单站无源定位模型的基础上，解析了其定位精度，并将Kalman滤波应用于相位差变化率的提取。随后分析了测量方位角精度、测相位差变化率精度等对定位精度的影响，从而提出了一种主要包括飞行设计及精度推算方法的等效替代精度试验方法。该等效替代精度试验方法已成功应用于装备的评估和试验，有较广的推广价值。

相位差变化率；单站无源定位；试验方法；等效替代

0 引 言

基于相位差变化率的单站无源定位技术是通过测量载机平台的速度、航向角和干涉仪的基线长度、信号的来波方向、频率、相位等参数，运算得出相位差变化率，并进行信号处理，达到对辐射源定位。由于基于相位差变化率的单站无源定位的优良性能（在20 s内达到2%R），对该定位的研究一直是热点。

目前对该技术的研究主要集中在定位模型的建立、定位性能分析、定位方法改进、相位差变化率提取、定位环境的影响分析（载机姿态、侦察信号样式等）［1～3］。定位模型主要确定观测参数，建立计算模型［4～6］，从而分析其定位性能［7～9］，并且提出了很多改进的定位和跟踪的改进算法［10～14］。对于相位差变化率的提取则集中在硬件的设计和滤波器的选取上［15～17］。

如何对基于相位差变化率的单站无源定位性能进行评估一直是学界研究的重点，对装备的研制极具重要意义。影响定位性能的各因素在定位结果中的贡献率如何、如何在有限的资源下评估较大空域范围内的定位性能是本文写作的初衷。本文提出的等效替代精度试验方法一定程度上能够节省试验资源、缩短试验周期、提高试验效率，并且通过对影响装备定位精度因素的分析，逐项剥离出各自的影响效果，是评估装备定位精度的合适选择。

1 基于相位差变化率的单站无源定位

不失一般性，定位精度模型考虑为二维。如图1所示，设平面坐标系xoy，S0（x0，y0）为固定辐射源位置，P（x，y）为雷达侦察分系统所在的载机位置，雷达信号频率为f，载机飞行速度为v，飞行方向为β，雷达侦察分系统与辐射源距离为R，辐射源相对载机的方位角为θ。

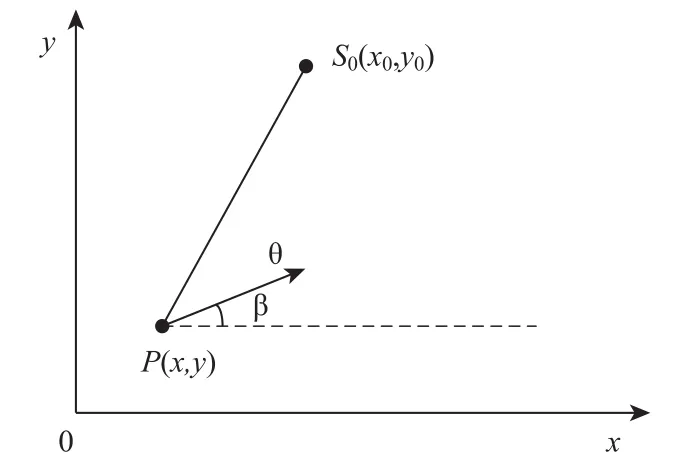
图1 观测站与辐射源位置关系图

依据几何关系有：

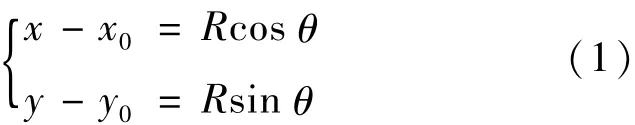
求导，得

化简，得

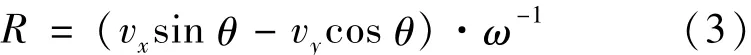
其中vx=d x/d t、vy=d y/d t、vR=d R/d t为飞行速度在x、y、R方向上的分量。ω=dθ/d t为到达角速度。又vx=v cosβ、vy=v sinβ，代入（3）式得

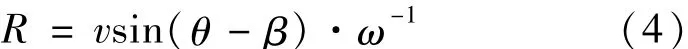
由相位干涉仪天线间的几何关系，有

对时间t求导，得

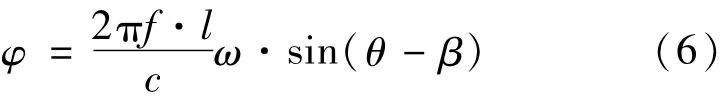
其中φ=dφ/d t为相位变化率，c为光速。将（6）式代入（4）式得到

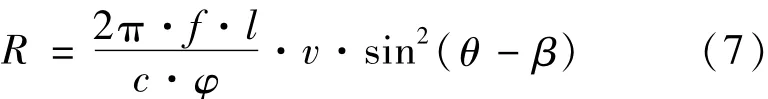
其中，v、β、P（x，y）由载机的导航设备实时给出，f由测频接收机实时给出，θ由测相接收机给出，φ可以由干涉仪接收机输出的相位φ通过快速运算得到。再利用（1）式就可以实现单机定位。不失一般性地在第i时刻，

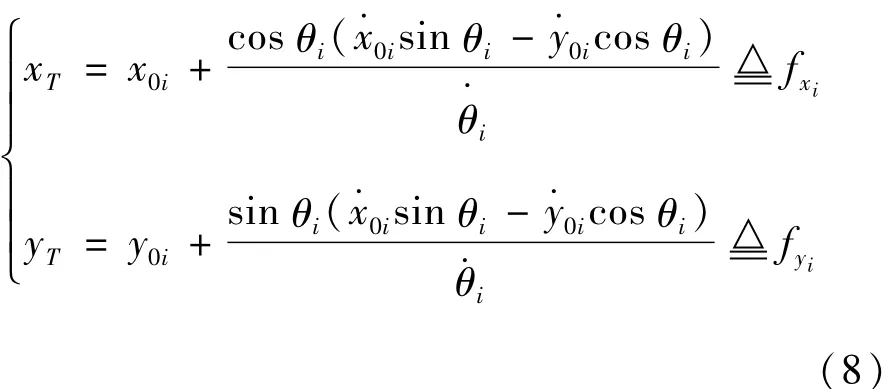
2 定位精度分析及相位差变化率的滤波提取

2.1定位精度分析

对定位精度的分析有两种方法，一种是在径向上分析误差在距离向的偏离程度，一种是分别分析正交的x、y方向上的精度，并合成为综合的径向误差。

首先分析其径向精度。

对（7）式进行误差分析，

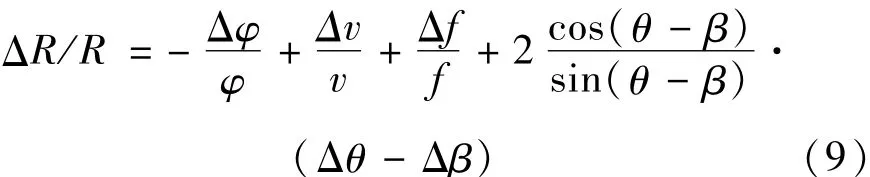
故

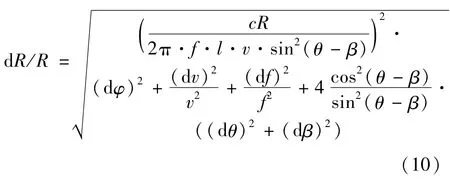
（10）式即为径向距离偏离的相对精度解析式。

再分析x、y方向上的合成精度，对（8）式求微分

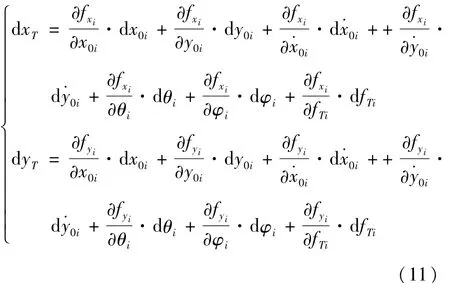
假设各项测量误差相互独立且服从零均值的高斯分布，并记E[( x0i)2]=E[( y0i)2]=，E

当测量误差较小时，可以近似地用“Δ”代替式（11）中的“d”，于是有E[(ΔxT)]=E[(ΔyT)]=0。二维定位几何稀释精度GDOP为

其中

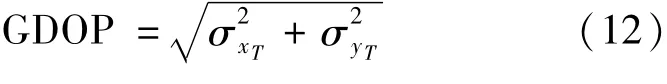
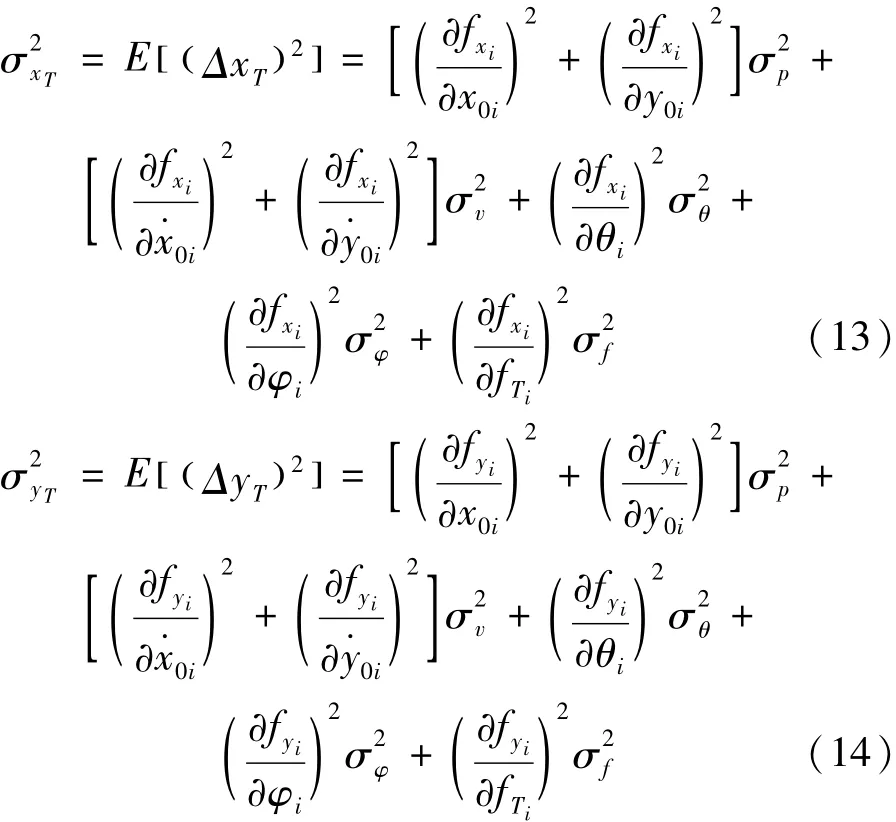
又对（8）式求偏导，可得

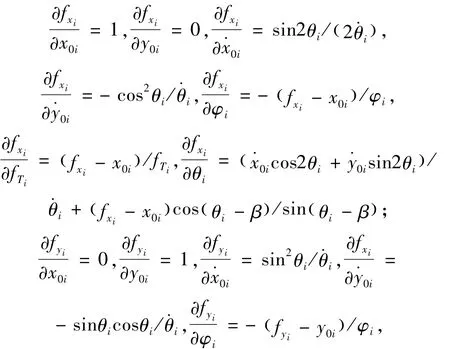
当c=3×108m/s，f=3×109Hz，v=300 m/s，D=10 m，β=0，σP=0，σθ=3×10-3rad，σv=0.1m/ s，σφ=3×10-3rad/s，σf=104Hz时，平面、三维单机相位差变化率定位精度分别如图2、图3所示。

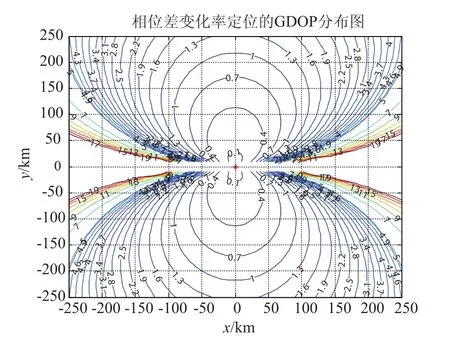
图2 平面单机相位差变化率定位精度示意图

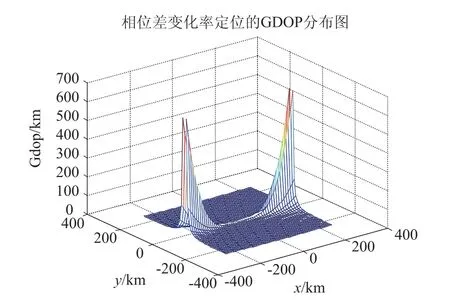
图3 三维单机相位差变化率定位精度示意图

由图2、图3可以看出，在定位平面上，定位精度呈圆状扩散状态；在空间上，随着高度的增加定位精度变差。

2.2相位差变化率的滤波提取

由2.1的分析可知，相位差变化率的提取对定位精度有着直接的影响，通常的方法主要有Kalman Filter（KF）、Extented Kalman Filter（EKF）、Unscented Kalman Filter（UKF）、最小二乘线性拟等。其中Kalman Filter已被广泛应用，设状态变量为Xi= [φiφi]T，观测周期为Ts，则可建立状态方程：

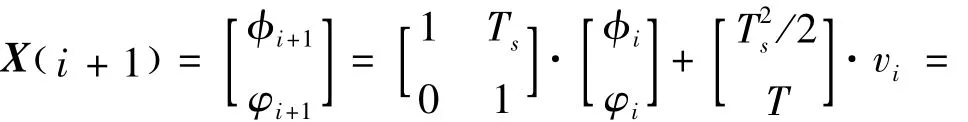
量测方程为：很显然，若过程噪声V()i～N 0，()q，量测噪声

W()i～N 0，()r，观测量φ的初始协方差P()1|1=

若X0=[56.9-0.14]T，Ts=1，r=4，q=1，仿真次数作为100次，得到的仿真结果如图4所示。

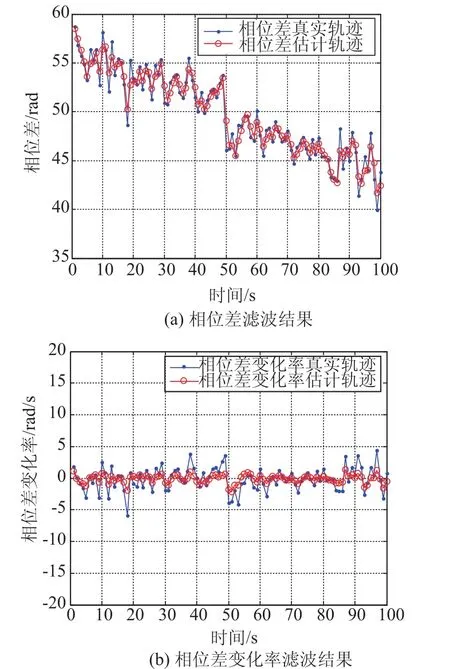
图4 基于kalman滤波的相位差及其变化率提取仿真示意图

3 等效替代精度试验方法

对于飞行方向角、光速、相位干涉仪天线间距离引起的测距误差可忽略不计。由式（8）、（10）、（12）可知，定位装备的定位精度与自定位精度、测频精度、测速精度、测相对方位角精度、测相位差变化率精度等因素有关，自定位精度与自定位装备的接收机的性能有关，飞行速度由载机的导航设备实时给出，频率由测频接收机给出，相对方位角由测向接收机给出，相位可由相位干涉仪接收机输出的相位获得，而相位差变化率则可通过对相位快速运算获得。

根据上节的分析，实际对定位精度影响较大的是测相对方位角精度、测相位差变化率精度，而自定位精度、测频精度、测速精度可以通过获得，在动态飞行的过程中，本文重点考虑测量方位角精度、测相位差变化率精度对定位精度的影响。

3.1测量方位角精度对定位精度的影响

传感器在保持一定的灵敏度的前提下，在一定的方位范围内能对目标进行侦察定位，其测向精度直接影响着定位精度。当σθ分别为6×10-3rad、9 ×10-3rad，其它条件同图2假设时，平面单机相位差变化率定位精度分别如图5、图6所示。

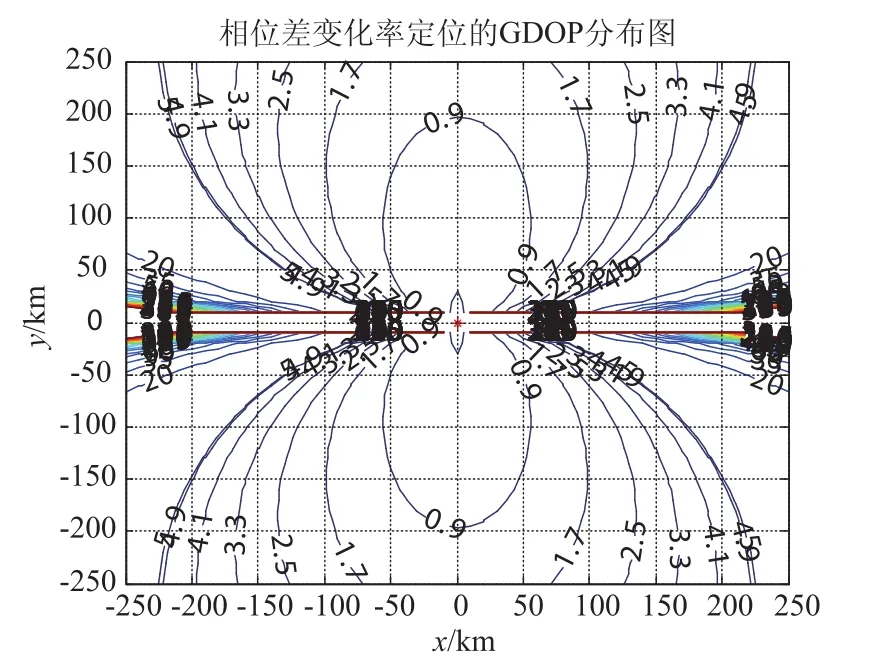
图5 σθ=6×10-3rad时定位精度示意图

图6 σθ=9×10-3rad时定位精度示意图

从图5、图6可以看出，随着测量方位角精度的变大，基于相位差变化率的定位精度在变差。当σθ从6×10-3rad变化到9×10-3rad时，坐标（100 km，100 km）处的定位精度从1.8 km变化到2.5 km。

3.2测相位差变化率精度对定位精度的影响

相位差变化率的精度与硬件设计、滤波算法等因素相关，同样是定位精度的主要影响因素之一。当σφ分别为6×10-3rad、9×10-3rad，其它条件同图2假设时，平面单机相位差变化率定位精度分别如图7、图8所示。

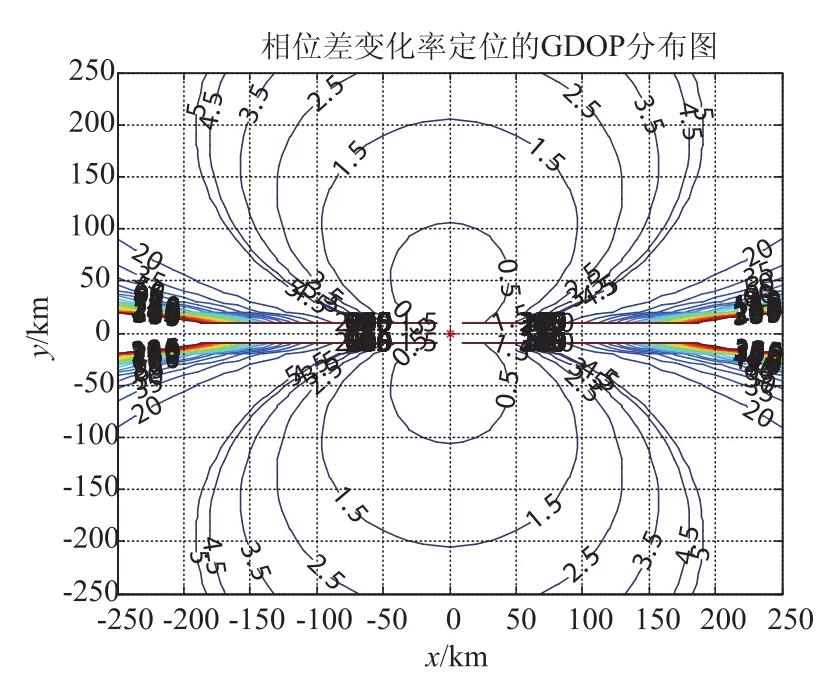
图7 σφ=6×10-3rad时定位精度示意图

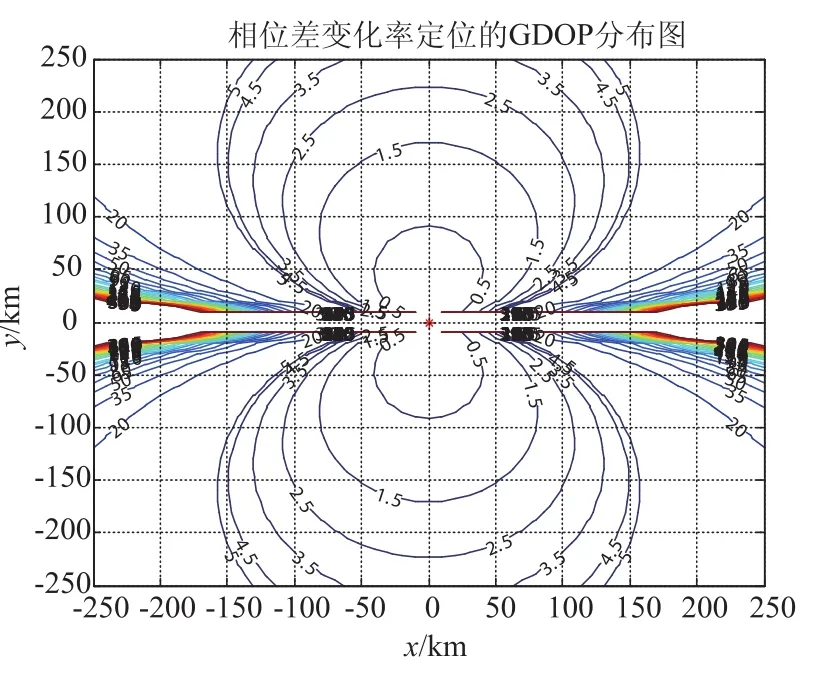
图8 σφ=9×10-3rad时定位精度示意图

从图7、图8可以看出，随着测相位差变化率的变大，基于相位差变化率的定位精度在变差。当σφ从6×10-3rad变化到9×10-3rad时，坐标（100 km，100 km）处的定位精度从1.6 km变化到2.0 km。

图5、图6、图7、图8分别分析了测量方位角精度和测相位差变化率精度对定位精度的影响。其定量关系如（10）式、（14）式所示，同时，（10）式、（14）式是单机相位差变化率无源定位的飞行设计及精度推算方法的理论基础。

3.3等效替代试验方法

对于特定的某部基于相位差变化率的单站无源定位系统，如何考核其对特定区域内分辐射源的定位精度是考核装备性能的难点。由于实际飞行时，飞行平台不可能遍及定位区域的所有定位，这就需要通过定位装备有限的飞行点位对辐射源的定位结果，选取合适的置信度，推算其对定位区域内任一点位的定位结果。

推算的基本思路就是：首先在理论上分析外场试验和期望试验中影响试验结果的各种因素，建立推算模型，其次设计一种典型的试验态势或战情想定，选择合适的试验替代对象，通过外场试验获得试验数据，再次将外场试验数据应用于推算模型，推算出对期望装备的试验结果。等效替代推算的原理框图如图9所示。

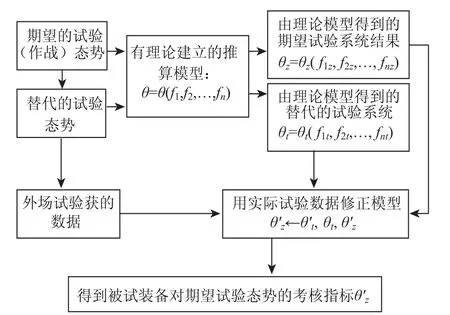
图9 等效替代推算的原理示意图

3.4单机相位差变化率无源定位的飞行设计及精度推算方法

忽略飞行方向角、光速、相位干涉仪天线间距离引起的测距误差σβ、σc、σl，测量自定位精度σp、测频精度σf、测速精度σv，测相对方位角精度σθ，根据在有限空域实飞得到的测相位差变化率精度σφ，从而推广得出更大空域的定位精度。

在某型装备的设计定型试验中，测得自定位精度σp=0.5 m，测频精度σf=10.5 kHz、测速精度σv=2.2 m/s，测相对方位角精度σθ=3.4×10-3rad/s，有限空域得到的测相位差变化率精度σφ= 9.2×10-3rad/s，由此计算推算得到定位精度结果如图10所示。

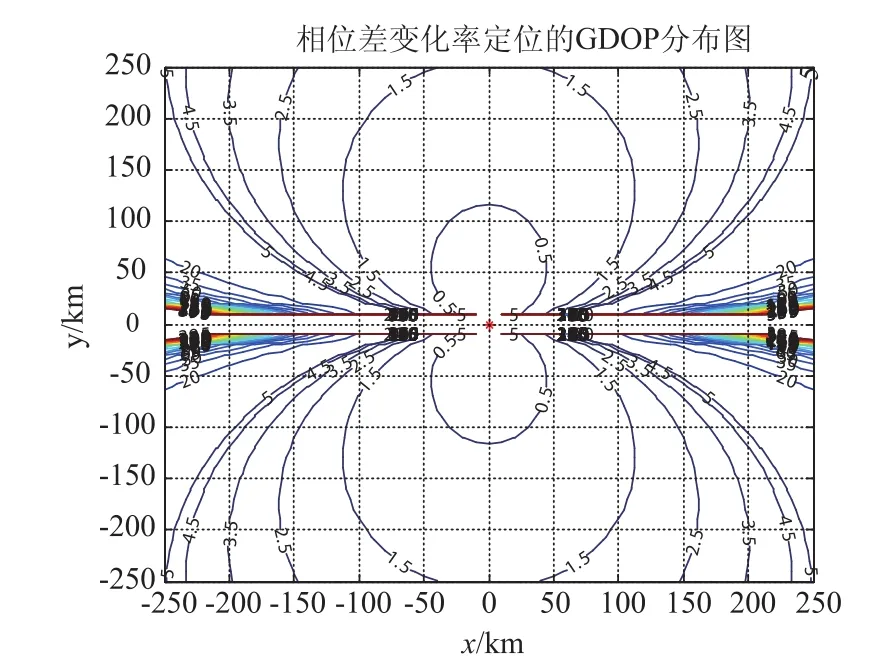
图10 某装备设计定型试验定位精度推算结果

4 结 语

基于相位差变化率的单站无源定位的技术已经比较成熟，影响定位精度的影响因素主要为相位差变化率的精度，提高相位差变化率的精度对于提高定位精度意义重大。基于有限的资源对定位装备的定位精度评估需要设计合理的航线和数据处理原则。本文讨论的被定位目标均是静止的，对动目标的高精度定位是亟待讨论、解决的论题。由于多普勒效应的存在，导致测频精度的不平稳，相位差变化率的时变等，这些因素对于定位精度的贡献率如何及如何评估，是进一步需要研究的问题。

［1］ 黄登才，丁敏.测相位差变化率无源定位技术评述［J］.现代雷达，2007，29（8）：32-33.

［2］ 李沛.机载单站无源定位技术研究［C］.长沙，电子对抗系统专业委员会第九届学术年会论文集，2014.9.

［3］ 刘聪锋.无源定位与跟踪［M］.西安：西安电子科技大学出版社，2011.6.

［4］ 单月晖，孙仲康，皇甫堪.基于相位差变化率方法的单站无源定位技术［J］.国防电子科技大学学报，2001，23（6）：74-77.

［5］ 高义，高元锋.基于相位差变化率的无源定位技术研究［J］.无线电工程，2013，43（1）：52-55.

［6］ 司文健，平殿发，苏峰，等.基于相位差变化率的机载无源定位研究［J］.舰船电子工程，2010，30（4）：76-79.

［7］ 李望西，黄长强，王勇，等.一种利用相位差变化率的机载单站无源定位方法［J］.电讯技术，2012，52（1）：13-17.

［8］ 夏韶俊，张海黎，徐龙.基于相位差变化率的单站无源跟踪算法研究［J］.航天电子对抗，2011，27（6）：55-58.

［9］ 刘永辉，窦修全.基于相位差变化率的单站无源定位技术［J］.无线电工程，2010，40（6）：48-50.

［10］乔梁.一种单站无源定位原理与目标跟踪算法研究［J］.上海航天，2007，（1）：16-19.

［11］宋德亮，张国毅，齐丽君.小波降噪在相位差变化率定位技术中的应用［J］.吉林大学学报（信息科学版），2009，27（3）：235-241.

［12］张国毅，宋德亮，王长宇，等.相位差变化率定位法中缺失值精确填补研究［J］.吉林大学学报（信息科学版），2010，28（1）：20-26.

［13］李望西，黄长强，王勇，等.利用相位差变化率的机载无源定位跟踪改进算法［J］.电子与信息学报，2013，35（1）：68-73.

［14］李望西，黄长强，王勇，等.利用相位差变化率的机载无源定位跟踪算法［J］.弹箭与制导学报，2012，32（5）：164-166.

［15］万方，丁建江，郁春来.一种雷达脉冲信号相位差变化率测量的新方法［J］.系统工程与电子技术，2011，33（6）：1257-1260.

［16］邓新蒲，祁颖松，卢启中，等.相位差变化率的测量方法及其测量精度分析［J］.系统工程与电子技术，2001，23（1）：20-23.

［17］丁静.提取相位差变化率的一种新方法［J］.无线电工程，2012，42（9）：26-27.

Research on Single Observer-Passive Location Based on Phase Difference Rate of Change and Test Method

ZHANG Zheng-chao，LIWen-chen，YUAN Xiang-yu，CHEN Yang，LIHong
（Luoyang Electronic Equipment Test Center of China，Luoyang 471003，China）

Orientational precision is analyzed based on buildingmodel of Single observer-passive location based on phase difference rate of change，and Kalman filter is applied in extracting phase difference rate of change in this paper.Then the effect of azimuth precision and phase difference rate of change precision in orientational precision are analyzed，and a equivalent precision testmeathod is put forward including fly design and precision calculating，this equivalent precision testmethod is applied successfully on evaluation and test of equipment，bearing extended value.

Phase Difference Rate of Change；Single Observer-Passive Location；TestMethod，Equivalent Substitute

TN97

：A

：1673-5692（2015）06-636-06

张政超（1981—），男，湖北武穴人，硕士，工程师，主要研究方向为雷达试验、雷达对抗试验的总体设计；

E-mail：15515363876@163.com；

李文臣（1972—），男，河北威县人，博士，高级工程师，主要研究方向为雷达试验、雷达对抗试验的总体设计；

袁翔宇（1974—），男，甘肃平凉人，硕士，高级工程师，主要研究方向为雷达试验、雷达对抗试验的总体设计；

陈 杨（1979—），女，四川武胜人，学士，工程师，主要研究方向为通信对抗试验鉴定评估；

李 宏（1969—），男，湖南岳阳人，博士，研究员，主要研究方向为雷达与雷达对抗、雷达与雷达对抗试验鉴定评估。

10.3969/j.issn.1673-5692.2015.06.014

2015-05-29

2015-08-15

总装重点课题