安全稳定性约束下的排土场优化设计

叶进霞

(山东省鲁南地质工程勘察院，山东 兖州 272100)

安全稳定性约束下的排土场优化设计

叶进霞

(山东省鲁南地质工程勘察院，山东 兖州 272100)

在保证露天矿排土场边坡安全稳定的情况下，优化排土场几何参数，达到在有限排土场范围内排土量最大的目的。根据排放物的物理性质，选择边坡平面滑动和圆弧滑动的安全稳定性系数为安全评价指标，利用排土场底面内接半径把排土场的边坡倾角、台阶高度与宽度联系到一起，分析三个指标之间的制约关系，将台阶宽度转化到台阶高度和边坡倾角的函数，分别对边坡倾角和台阶高度进行分段求取，多次模拟计算，得出一组接近于最优解的值作为排土场设计的最佳模型。实验结果表明，和其他方法比较，本文算法考虑了安全稳定性约束条件下，实现排土场设计尽量多排土、少占地的目的。

安全稳定性系数；分段求解；最优模型；排土场容积

露天采煤的第一个任务是剥离表土，需要剥离煤层上部的岩土，排弃大量的岩石和土壤，尤其较深的露天矿，往往占用较多的农田。排土场应选择在靠近采矿场，尽量回填采空区，少占农田，有条件的应放置在山谷、洼地处，注意环境保护和造田、还田。排土场占用大量的农田，不仅破坏环境，而且需要赔付耕地补偿，很多矿山企业都对排土场进行了复垦，但是排土场的结构并不适合种植，投入大量的资金需要改善排土场，并且复垦土地的经济效益不如原有土地[1]。

目前，对排土场优化设计的相关研究中，任高峰等提出了优化设计露天矿的边坡空间形状，最大限度的减少岩土剥离量，以达到减少占地的目的[2]；郭成等提出了基于安全稳定性的大容积排土场堆置要素优化，但是没有将给出具体的体积计算方法[3]；卫博等提出了基于圆锥模型的节地复垦排土场设计模型，但是没有考虑排土场的安全稳定性，只分析了引起排土场面积和容积的变化关系，没有提出确定最佳模型的方法[4]。因此，本文在排土场各种物理属性确定的情况下，分析人为控制的排土场因素与排土场边坡安全稳定性、排土场容积之间的关系，保证排土场边坡安全稳定性的情况下[5-8]，利用分段模拟法，使设计范围固定的排土场的最大容积，减少排土场占用土。

1 排土场边坡稳定性分析

排土场稳定性是影响排土场占地面积的关键因素，排土场参数的选择关系到排土场设计的合理性。影响露天矿排土场边坡稳定性的因素很多，排土场边坡滑动的类型主要包括平面滑动和圆弧滑动。

1.1 无确定拉张裂缝的平面滑动稳定性系数

边坡破坏时，滑动面为平面或近似平面时的滑动为平面滑动。露天矿排土场的土质相对较均匀，没有确定的滑面，也没有确定的拉张裂缝，通过分析可以求得排土场的最危险的滑面和最可能出现拉张裂缝的位置[9-10]。图1(a)为平面滑动示意图。

平面法分析边坡稳定性时，滑面倾角小于边坡倾角，滑体在受到自身重力作用下，沿着滑面向下滑动，边坡稳定性系数计算公式见式(1)。

(1)

式中：Fs平为边坡稳定性系数；γ为排弃物的容重；C为滑面上的单位粘聚力；φ为内摩擦角；H为排土场台阶高度；Z为垂直裂面高度；α为排土场边坡倾角；β为滑面倾角。其中γ、C、φ由排土场排弃物的物理属性决定，最危险滑面的倾角β=(α+φ)/2，H和α根据实际情况设计，根据Fs平的极小值可求出拉张裂缝的临界高度Z。

根据图1(a)可知，在台阶上部最可能出现平面滑动的位置到台阶边缘的距离D1=H(cosβ-cosα)，D1为平面滑动最危险距离，在设计排土台阶时，台阶宽度应大于最危险距离D1。

1.2 圆弧滑动的稳定性系数

圆弧滑动是指排弃物的滑面呈圆滑形状的岩土滑动。圆弧滑动的基本假设条件：均质粘性土坡滑动时，其滑动面常近似为圆弧形状，假定滑动面以上的土体为刚性体，即设计中不考虑滑动土体内部的相互作用力，假定土坡稳定属于平面应变问题。图1(b)为圆弧滑动示意图。

圆弧滑动的稳定性系数的基本公式为：取圆弧滑动面以上滑动体为脱离体，土体绕圆心O下滑的滑动力矩为Ms=Wa，阻止土体滑动的力是滑弧AFD上的抗滑力，其值等于土的抗剪强度与滑弧长度的乘积，稳定系数Fs圆=抗滑力矩/滑动力矩，见式(2)。

(2)

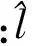
(3)

滑动力矩由滑动圆弧内的排弃物的作用力引起，滑体ABDF为三角体ABD和弓形体AEDF之和，而弓形体AEDF为扇形体AODF与三角体AOD之差，其各自的力矩见式(4)～(7)。则滑动力矩可表达为式(8)。

(4)

(5)

(6)

(7)

(8)

式中：H为排土场台阶高度；C为沿弧面的粘聚力；ω为弧心角之半；α为排土场边坡倾角；β为弧弦的倾角；R为圆弧滑面半径。其圆弧滑面半径的计算公式见式(9)。沿弧面的粘聚力的计算公式见式(10)。

(9)

(10)

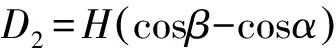
2 排土场容积推导

在排土车或者输送皮带将排弃物运送到排土场并直接倾倒在排土场时，排弃物在重力的作用下，根据排弃物的颗粒大小以及密度等性质，排土场各个方向的边缘都接近于圆弧形状，台阶式排土场的各个台阶也就近似圆锥台[11]，如图2所示。

图2 台阶设计示意图

由于排土场的基底是不规则的面，处于排土场底部最高点以下的容积不能用视为圆锥台，处于基底最高点下部的体积用不规则三角网TIN即可计算得到。基平面以上的部分每一级台阶分为一个圆锥台体，每一个台阶柱体的体积计算公式见式(11)。

(11)

式中：Si下和分别为第i个台阶上下面的面积；hi下和hi上分别表示第i个台阶上下面所在圆锥台的高。由于排土场的各个台阶的侧边缘接近于圆弧形状，再根据三角形相似性的性质，排土场台阶的上下两个面的面积满足式(12)、式(13)。

(12)

(13)

式中：S上、S下分别代表排土场台阶上下面的面积；r为台阶下底面的内接半径；d为台阶宽度；H为台阶高度。上下两个台阶的下底面的内接半径关系见式(14)。将式(12)和式(13)代入式(11)得到这个排土场的容积，见式(15)。

ri+1=ri-Hictgα-d

(14)

(15)

式中：V0表示基平面下部的容积，利用排土场底面的三维点构建的TIN求得。

3 最佳模型模拟设计

排土场设计时，排弃物的物理性质由矿区地质环境决定，因此要提高排土场安全性和排土场容积只能调整排土场边坡倾角α、台阶高度Hi与宽度di，结合排土场实际情况和排弃物的性质，协调三个量使排土场保证安全的情况下达到最大的容积，减少排土场占地面积。排土场平面滑动和圆弧滑动的安全稳定系数以及排土场容积的计算公式都涉及到α、Hi、di三个变量，各个排土台阶的底面内接半径ri也由这三个变量决定，其余各个量由排弃物的物理性质或排土场的环境决定，不能人为地改变。选定排土场范围之后，排土场基底面的内接半径r0底确定，确定边坡倾角和台阶高度之后，平面滑动和圆弧滑动的最可能出现滑动的位置都相应确定，为了削弱上下台阶之间的相互影响，设置台阶宽度为两种滑动中的最危险距离，即d=max(D1,D2)，由此减少一个变量。

在两个安全稳定性的约束下，α、Hi增加到一定值时，受到安全因素的影响，继续增大α、Hi的值，台阶级数必然减少，V的值也减小。由于Fs平、Fs圆、V与变量α、Hi的关系都比较复杂，无法用常规的方法进行规划并求V的最大值，因此采用分段求最值的方法，确定一个值的情况下，求另一个值使得V最大，分别对α、Hi进行两次分段求V的最大值，求得的α、Hi使V的值接近于最大值。

4 验证实验

研究区域范围的面积为60492m2，内接半径为437m，区域内的最高点和最低点的高程分别为478m和418m，排土场基底最高点以下部分的容积为72.39万m3。由于排弃物的颗粒大小、质地等不一样，选择各个参数的平均值作为整个区域的参数值。其中，内摩擦角为46°，容重1.75kN/m3，单位粘聚力为1.50MPa。

边坡倾角从0°到45°，以3°为间隔，保证平面滑动稳定性系数和圆弧滑动稳定性系数都大于1.2的情况下，分别计算得到对应的台阶高度与宽度、台阶级数、排土场容积，计算结果见表1。

从表2 中可以看出，在所有的模拟值中，当边坡倾角为33°，对应的台阶高度为35.47m，该排土场的容积最大，可知该区域的最佳模型的边坡倾角在33°附近。因此，在台阶高度的基础上，对33°的左右两个分段区间再进行分段计算，边坡倾角30°和36°对应的最佳台阶高度为37.59m和33.58m，则从33.5m到38m按照0.5m进行分段，计算结果见表2。

按照分段计算得到台阶高度为36m以及台阶宽度为32m时，对应边坡倾角为32.53°，研究区域的排土容积最大，即该区域内排土台阶设计的最佳模型为：当边坡倾角32.53°，台阶高度36m，台阶宽度32m，台阶级数4级时，基平面上方的容积最大，为134.73万m3。

表1 按边坡倾角的分段结果

表2 按台阶高度的分段结果

5 结 论

本文提出的模型是将排土场三维表面模拟为圆锥形，对于一些特殊情况可以把排土场表面简化近视为圆锥。在保证边坡平面滑动和圆弧滑动的安全稳定性系数大于1.2的情况下，协调边坡倾角、台阶高度和宽度三者之间的关系，使得给定范围内的排土场内排土容积达到最大值，减少排土场占用土地面积。台阶式排土场基底面的内接半径将边坡倾角、台阶高度、台阶宽度以及排土场高度联系到了一起，形成彼此之间相互限制的关系，将最有模型转化到边坡倾角和台阶高度的二元函数之后，两次分段查找体积最大的点，该点对应的三个参数值接近于排土场设计的理想模型，可认为是台阶式排土场设计的最佳模型。在实际操作过程中，很难控制三个参数和设计值完全一致，因此保证三个参数值在一定容差范围内即可。

[1] 马从安,才庆祥,韩可琦.露天矿生产与生态重建适宜性评价专家系统[J].中国矿业大学学报,2006,35(2):231-234.

[2] 任高峰，张世雄.深凹露天矿边坡空间形状优化设计[J].采矿与安全工程学报,2006,23(4):472-475.

[3] 郭成,马萃林.露天矿排土场堆置要素的优化[J].金属矿山,2011(1):42-45.

[4] 卫博,付梅臣,白中科,等.基于节地的露天矿排土场设计[J].农业工程学报,2006,22(6):230-232.

[5] 蓝航,李凤明,姚建国.露天煤矿排土场边坡下采动沉陷规律研究[J].中国矿业大学学报,2007,36(4):482-486.

[6] 石建勋,刘新荣,廖绍波,等.矿区排土场堆载对边坡稳定性影响的分析[J].采矿与安全工程学报,2011,28(2)：258-264.

[7] 李小春，任伟，王少泉，等.论金属矿山排土场设计规范中边坡极限平衡计算方法的选取[J].岩石力学与工程学报，2011，30(S2)：4136-4142.

[8] 汪海滨，李小春，米子军，等.排土场空间效应及其稳定性评价方法研究[J].岩石力学与工程学报，2011，30(10)：2103-2111.

[9] 蒋斌松,蔡美峰,都浩.平面滑动边坡稳定性的解析计算[J].岩石力学与工程学报,2004,23(1)：91-94.

[10] 吴侃,李亮,敖建锋,等.开采沉陷引起地表土体裂缝极限深度探讨[J].煤炭科学技术,2010,38(6):108-112.

[11] 蔡利平,李钢,史文中.增地节地型露天矿排土场优化设计[J].煤炭学报，2013，38(12)：2208-2214.

Optimized design of dump based on the security and stability

YE Jin-xia

(Shandong Lunan Geo-engineering Exploration Institute，Yanzhou 272100，China)

The dump geometric parameters were optimized to achieve the maximum volume of dump within the limited range under the condition of the safety and stability of the open-pit dump.The security and stability factor of plane and circular sliding were selected to evaluate the safety based on the physical properties of emissions.Relationship between three indexes，slope angle，step height and width，were analyzed，followed by the computation of step height and slope inclination segment by segment.The values close to the optimal solutions were obtained via simulations.The experiment shows that，when the method takes into account the Security and Stability Constraint，the proposed method can pile up more solid waste and occupy less land than other methods.

security and stability factor；segmented solving；optimal model；dump volume

2014-04-03

叶进霞(1977-)，男，山东东平人，工程师，主要从事水文地质、工程地质、环境地质工作。E-mail：yejinxia1977@163.com。

TD 216

A

1004-4051(2015)05-0153-04