Heisenberg型的群上的Radon变换

何建勋，李宗涛

（1.广州大学数学与信息科学学院，广东广州 510006；2.广州民航职业技术学院人文社科学院，广东广州 510403）

Heisenberg型的群上的Radon变换

何建勋1，李宗涛2

（1.广州大学数学与信息科学学院，广东广州 510006；2.广州民航职业技术学院人文社科学院，广东广州 510403）

令H＝｛（z，t）：z∈Cn，t∈Rm｝表示Heisenberg型群，对于（z，t），（z′，t′）∈H，群乘法法则为（z，t）°（z′，t′）＝（z＋z′，t＋t′＋zJz′t），其中zJz′t＝（z U（1）z′t，z U（2）z′t，…，z U（m）z′t），z′t表示z′的转置，U（j）（j＝1，2，…，m）是2n×2n反对称实正交矩阵，文章给出了H上的Radon变换，并通过Fourier变换得到了与映射J相关的逆公式.

Heisenberg型的群；Radon变换；逆公式

众所周知，Heisenberg群是二步的幂零Lie群的典型代表，它是非紧非交换的群，Heisenberg群上的调和分析以及Radon变换理论可参见文献［1－5］.Heisenberg型的群简称H型的群，是Heisenberg群的推广，它的中心的维数m≥1，在几何上有其重要的意义，关于H型的群上的调和分析见文献［6－10］.本文考虑的是H型的群上的Radon变换问题，由Fourier分析的理论得到相应的逆算子的表达式.

1 一些基础知识

2 H型的群上的Radon变换

先介绍H群的表示论方面的知识：设N表示非负整数集合，k∈N，x∈R，Hermite多项式Hk（x）定义：

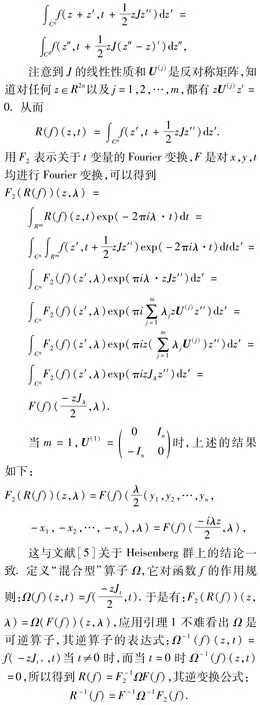
一般地说，一个可积函数的Radon变换不一定仍是可积函数［5］，换种说法是平方可积函数的Radon变换不一定还是平方可积的，因此将寻找L2（H）的子空间，使Radon变换在这个子空间上是单射满射.其中变量t是群的中心变量.而当考虑四元数Heisenberg群的类似问题时，（）n被四元数Heisenberg群关于中心变量的Laplacian算子所代替［11］，但是需要计算R（f）的群Fourier变换.然而，在H型的群上，当时，R（f）的群Fourier变换在相应的正交基下的表达式已在文献［3］中给出，但对于一般的H型群，由于群运算涉及的映射J是m个一般形式的反对称矩阵之和，使得函数的Radon变换后的群Fourier变换的计算十分困难，这个问题留到后面研究.

［1］ FOLLAND G.Harmonic analysis in phase spaces［M］.Princeton，NJ：Princeton University Press，1988.

［2］ GELLER D.Fourier analysis on the Heisenberg group［J］.JFunct Anal，1980，36：205-254.

［3］ HE JX.An inversion formula of the Radon transform on the Heisenberg group［J］.Canad Math Bull，2004，47：389-397.

［4］ RICCIF，SJÖGREN P.Two parametermaximal functions in the Heisenberg group［J］.Math Z，1988，199：565-575.

［5］ STRICHARTZR S.Lpharmonic analysis and Radon transforms on the Heisenberg group［J］.JFunct Anal，1991，96：350-406.

［6］ COWLINGM，DOOLEY A H，KORANYIA，etal.H-type groups and Iwasawa decompositions［J］.Adv Math，1991，87：1-41.

［7］ BONFIGLIOLIF，UGUZZONIF.Nonlinear Liouville theorems for some critical problems on H-type groups［J］.JFunct A-nal，2004，207：161-215.

［8］ LIU H P，WANG Y Z.A restriction theorem for the H-type groups［J］.Proc Amer Math Soc，2011，139：2713-2720.

［9］ MÜLLER D，STEIN E M.On the spectralmultiplier for the Heisenberg and related groups［J］.JMath Pures Appl，1994，73：413-440.

［10］YANG Q H，ZHU F L.The heat kernel on the H-type groups［J］.Proc Amer Math Soc，2008，136：1457-1464.

［11］HE JX，LIU H P.Wavelet transform and Radon transform on the Quaternion Heisenberg group［J］.Acta Math Sin（Engl Ser），2014，30：619-636.

The Radon transform on the Heisenberg-type groups

HE Jian-xun1，LIZong-tao2

（1.School of Mathematics and Information Sciences，Guangzhou University，Guangzhou 510006，China；2.School of Humanities and Social Sciences，Guangzhou Civil Aviation College，Guangzhou 510403，China）

Let H＝｛（z，t）：z∈Cn，t∈Rm｝be the Heisenberg-type groups.For（z，t），（z′，t′）∈H，the group multiplication is given by（z，t）◦（z′，t′）＝（z＋z′，t＋t′＋zJz′t），where zJz′t＝（z U（1）z′t，z U（2）z′t，…，z U（m）z′t），z′tdenotes the transpose of z′，and U（j）（j＝1，2，…，m）are real skew-symmetric orthogonalmatrices.In this paper，we give the definition of the Radon transform on the Heisenberg-type groups，and obtain an inversion formula related with themapping J by Fourier transform.

Heisenberg-type groups；Radon transform；inversion formula

O 174.2

A

【责任编辑：周 全】

1671-4229（2015）03-0001-03

2015－01－30

国家自然科学基金资助项目（11271091；11471040）

何建勋（1956－），男，教授，博导，博士.E-mail：hejianxun＠gzhu.edu.cn