突发信号前向频偏估计方法综述

杨晗竹，李广侠，赵陆文，杜 锋

（解放军理工大学 通信工程学院，江苏 南京 210007）

突发信号前向频偏估计方法综述

杨晗竹，李广侠，赵陆文，杜 锋

（解放军理工大学 通信工程学院，江苏 南京 210007）

突发通信具有抗干扰、低截获等优点，已成为数字通信的重要方式。在突发通信模式的载波同步问题中，前向频率估计算法因具有估计速度快、不存在挂起现象的优点而得到广泛使用。介绍了频域上的Rife算法和Quinn算法，时域上的Fitz算法、L＆R算法和M＆M算法几种经典频偏估计方法，分析了算法的基本思想并对其进行了数值仿真和性能比较。其次，介绍了几种近些年的最新算法，这些算法相对于经典算法在一定程度上有了很大改进，但是在实际应用中依然存在一些局限性，因此，进一步了解并提出计算更加简单、精度更高、估计范围更广的高效频率估计算法依然是当前的发展方向。

突发信号；载波同步；前向频偏估计

0 引言

突发通信具有抗干扰、低截获等优点，现被广泛应用于卫星通信、军事通信等领域，但突发通信信号持续时间短，对信号的快速捕获、跟踪以及解调提出了较高的要求。在无线数字通信系统中，由于各种因素，如多普勒频移、多径衰落以及本地振荡器的不稳定等造成信号的损耗，使载波难以同步，而在这些损耗中，最影响接收性能的一个原因是频率偏移。信号传输中的频偏会引起载波间的干扰，从而导致性能的下降，严重时会导致无法解调出原始信息。为了正确地解调信号，必须对载波频率进行高精度估计，使系统达到很好的载波同步。

目前为止，国内外已经对突发通信中的频偏估计提出了不少方法，依原理的不同，提出了多种分类方法，本文主要按照频域、时域及时频分析方法进行分类。

1 频偏估计算法性能评价标准

在无线高速突发通信系统中，要求对载波能够进行快速恢复，目前公认的评价频率估计方法的性能指标主要有估计均值、估计方差、估计范围、计算复杂度和信噪比门限值等［1］。

均值表明估计算法是有偏的还是无偏的，方差则反映估计算法的估计精确度。一个较完美的频偏估计算法一定是无偏的且方差很小。克拉美罗界［2］（Modified Cramer-Rao bounds，MCRB）通常被用来作为一个算法估计精度的标准，并且可从关于方差的仿真图中大体判断出信噪比门限值。估计范围定义为f0／fs，即归一化频偏，f0为载波频偏，fs为采样频率。受奈奎斯特采样定理的限制，频偏的最大估计范围是（－0．5～0．5）。计算量在工程中影响实现复杂度，在实际情况下，计算复杂度与估计精度、估计范围等相矛盾，这是目前算法急需解决的问题之一。

2 频域算法

2.1 典型频域算法

2.1.1 Rife算法

Rife D C和Vincent G A于1970年提出Rife频率估计算法［3］。该算法采用插值方法，计算出矫正偏差δ，从而推算估计频偏。

信号采样值x（n）的N点FFT记为X（k），X（k）最大谱线的幅度记为，次大谱线的幅度记为。根据比值得到信号实际与估计频率之间的相对偏差则信号的实际频率估计为：

式中，Δf为频率分辨率，并且正负号根据次大值相对于最大值的位置确定。

2.1.2 Quinn算法

Quinn算法［4，5］利用相位信息，定义：

2.2 算法性能比较

对Rife和Quinn算法进行比较，其结果如图1所示。由图1可知，在信噪比大于－3 dB时，随着信噪比的增大，Quinn算法频偏估计性能相对于Rife算法较好。这是由于Quinn算法在|δ|较小时，X（m＋1）与X（m－1）的相位差为180°，不容易出现插值方向错误，从而避免在δ较小时存在误差激增问题［6］。

图1 Rife算法和Quinn算法频偏估计误差方差

两种算法均对小频偏不敏感，且在数据长度短时估计精度不高，数据长度长时复杂度增加，因此在实际工程中适用性较差。

3 时域算法

时域频偏估计主要是基于最大似然前馈结构的载波频偏估计算法。在数据辅助类方法中，算法主要借助导频来提取载波同步的信息，从接收信号的样本中直接估计出载波同步的必要参数，如载波频率［7］。该类方法同步建立时间较短，载波失步后重新捕获较快，而且没有一般锁相环的挂起现象，因此适用于突发信号的捕获。

在这类算法中，需先计算信号的自相关函数，定义信号z（k）的自相关函数为［8］：

3.1 典型时域算法

3.1.1 Fitz算法

Fitz M.P.提出了Fitz算法［9］，这是一种基于前馈结构的载波频率估计算法。算法的关键在于对信号的自相关序列取相位以得到相位序列，通过对相位序列求算术平均，得到载波频率估计值。其频率估计式为：

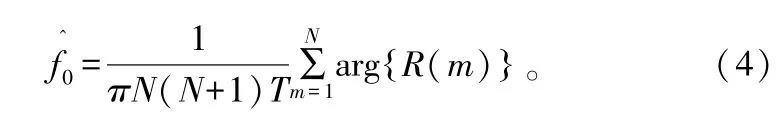
由图2和图3可知，随着采样点数L的增加，Fitz算法频率估计精确度得到提高，并且信噪比要求降低。因此，Fitz算法适合于低信噪比条件下对长序列进行频偏估计。

图2 Fitz算法频率估计均值

图3 Fitz算法频率估计方差

3.1.2 L＆R算法

Luise和Reggiannini于1995年提出了L＆R算法［10］。与Fitz算法不同的是，L＆R算法对信号的自相关序列R（m）进行了取平均值，如图4所示这对减小噪声的影响有一定意义。频率估计表达式如式（5）所示：

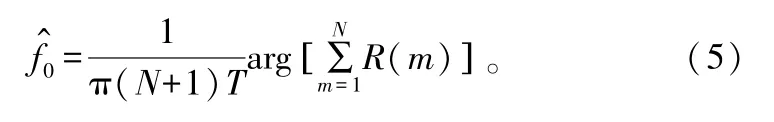
图4 L＆R算法频率估计均值

该算法信噪比门限值大约为0 dB，但由于受到较窄的频率估计范围的影响，如图5所示，其多应用于收发双方动态性较低的突发通信系统。

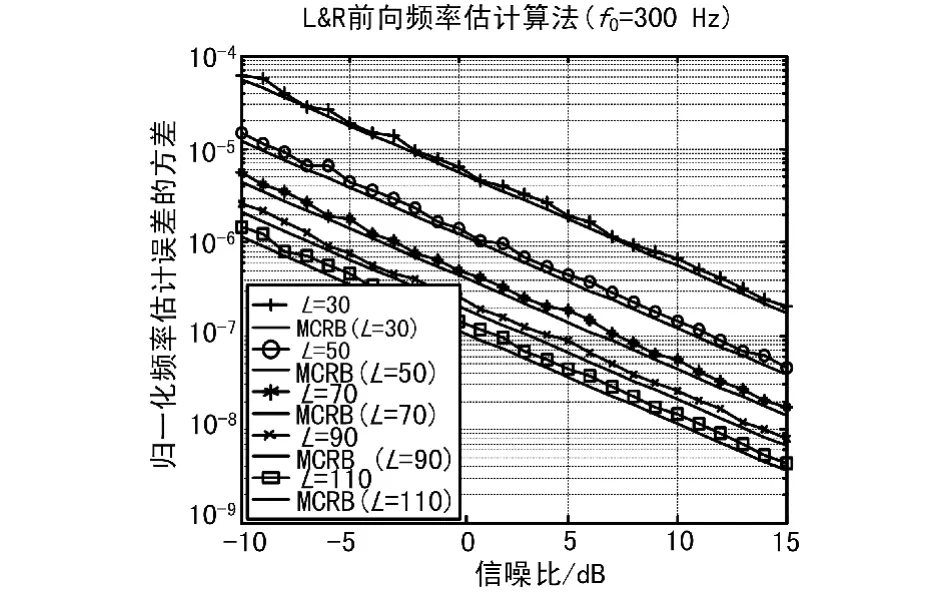
图5 L＆R算法频率估计方差

3.1.3 M＆M算法

Umberto Mengali和M.Morelli于1997年提出了M＆M算法［11］。这也是一种前向结构的载波频率估计算法。该算法对自相关函数的相位差分结果进行平滑，并将平滑结果作为载波的频率估计值，如图6所示。算法的频率估计表达式如式（6）所示：

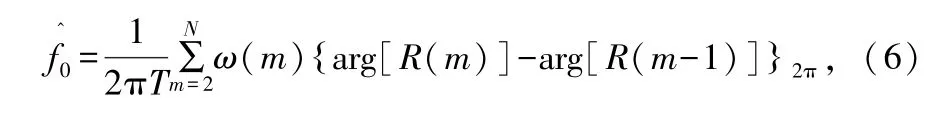
式中，ω（m）为平滑函数，表达式为：

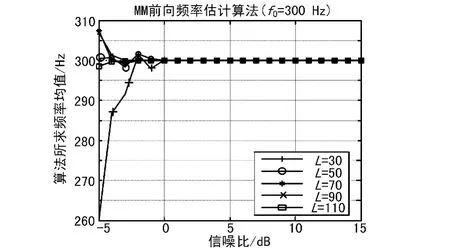
图6 M＆M算法频率估计均值

由仿真可以看出，M＆M算法在有效频偏估计范围内，估计误差较小。虽然其收敛的信噪比门限较高，但其在低信噪比的条件下，几乎能达到频率估计的理论极限（MCRB）。该算法建立了频率与相位增量之的函数关系，其具有较大的频率估计范围。

3.2 算法性能比较

3.2.1 算法频偏范围估计

图7给出了3种不同的基于相关系数的算法的频偏估计范围曲线图。

从图8可以看出，M＆M算法的估计范围最大，适用于大频偏的估计；Fitz算法估计范围最小，L＆R算法是Fitz算法估计范围的两倍。表1给出了3种算法的理论的估计范围［12］，容易看出，仿真结果与表所示的内容相契合。

图7 M＆M算法频率估计方差

图8 3种不同算法频偏估计范围曲线

表1 3种频率估计算法的估计范围

3.2.2 算法计算复杂度比较

表2 3种估计算法的计算复杂度

4 频偏估计优化算法

基于自相关函数的频偏估计法作为前向频率估计方法的一种重要类型，当前被广泛使用，但是已有的经典算法在估计精度、估计范围和信噪比门限上普遍存在矛盾。近些年，有很多研究者在经典算法的基础上研究出了一些优化算法，在性能上有所提升。

4.1 典型优化算法

4.1.1 分段累加方法

文献［14］在线性预测方法的基础上，提出了将接收信号首先取采样值，再进行分段累加，然后求累加值的自相关函数，进而求得频率值的方法。分段累加算法具有计算简单，运算量小的优点，但是其信噪比门限太高，大于5 dB，而且估计方差很大。因此通常用于高信噪比条件下的快速频偏估计。在某些频偏估计算法中，估计精度的提高是以增加计算量和减小估计范围为代价的，而分段累加方法随着数据长度的增加计算复杂度相应会降低，同时估计精度也得到了提升，但是频偏估计的范围会相应减小，在具体的工程实现中必须结合实际的条件在各性能之间进行折中。

4.1.2 相邻自相关函数共轭相乘法

文献［15］提出了一种适用于大频偏和低信噪比条件下的载波频率估计算法。这种算法先计算出信号的自相关函数，接着进行采样得到自相关序列，再对相邻自相关共轭相乘，对该结果求取相位值，最后从相位值推算出频率估计值［16－18］。该算法的优势在于工作的信噪比门限较低，大约能达到－3 dB，在低信噪比下比Kay算法要好得多；频偏估计范围较大，几乎能够达到－0.5～0.5，更适用于诸如低轨卫星通信系统等信号具有高动态和低信噪比的应用场合。但是该算法估计值精确度较低，较大地偏离了克拉美罗界。

4.1.3 求自相关采样共轭加窗法

文献［19］提出了一种适用于低信噪比和大频偏条件的频率估计算法，此算法将信号的自相关函数等效为一种复载波信号的采样序列，再对此序列相邻两点共轭相乘，求相位，该算法参考了Kay算法基于点差分的特点，利用相邻数据点差分获得频率估计序列，这些估计值相互统计独立，对这些估计值进行一定的加权处理后得到的频率即设定为估计的载波频率估计值。他的创新点体现在用矩形窗函数对所得相位平滑，最后以平滑结果对载波频率进行估计。此算法频率估计范围大，在SNR为10 dB的情况下，归一化频偏估计范围能够达到－0.5～0.5；在SNR为2 dB的时候，频偏估计范围也能够有－0. 45～0.45。在信噪比小于0 dB的条件下进行频率估计取得的效果也较好，比较适合应用于大频偏、低信噪比的情况。

4.1.4 基于Quinn算法的改进Rife算法

文献［20］提出了一种基于Quinn算法与改进的Rife算法的正弦信号频率估计算法。一般情况下，在信噪比较低或者相对偏差较小时，会存在插值方向错误的情况。对此，该方法将Rife算法与传统的Quinn算法结合，提出了一种基于相对偏差的FFT变换估计的新算法。该算法利用主瓣内最大幅值与次大幅值的中间幅值，对原本有较大偏差的Rife算法进行了改进，而且计算量基本没有增加。由仿真结果可以知道，新算法估计误差小，估计性能优于传统的Rife算法和Quinn算法。然而，该算法的相位信息受噪声影响较大，信噪比门限也较高，约为10 dB，因此，需要在研究中进行进一步的改进。

4.1.5 相关测频算法

在现有频率估计方法的基础上，文献［21］在FFT的基础上，结合相关系数，提出了一种新的频率估计算法，称之为相关测频算法。该方法先运用DFT或FFT的方法对频偏求得粗估计值，然后再运用相关系数求出微估计值，粗估计值和微估计值相加再通过相应关系推导出频偏估计值。理论研究和仿真分析表明：当被估计信号的信噪比较大时，该算法的估计误差接近MCRB下界。但是当信号中噪声较大时，会出现频域算法普遍存在的问题，即通过FFT不能准确给出信号的粗频率估计值，这是一个亟待解决的问题。相关测频算法与迭代插值FFT估计算法［21］和改进Rife算法［22］相比，估计精度略有降低，但计算量下降了很多，适合工程上的应用。

4.1.6 基于自相关函数的频率估计方法

文献［23］提出了一种新的基于自相关函数的频率估计算法。该方法先对归一化的自相关函数计算相邻共扼乘积，通过近似处理将乘积表达式中信号与噪声的乘积关系转化为相加关系，然后推导满足最大似然估计准则的窗函数，并对乘积加权平均，最后通过求解辐角主值获得频率估计值。该方法借鉴了M＆M算法的特点，避免了直接对自相关函数求辐角主值，因此频偏增大时，依然保持较低的信噪比门限。从仿真分析也表明只要频偏值不接近理论极限值，该算法的信噪比门限基本与频偏大小无关，即大频偏时依然保持低信噪比门限。说明频偏越大该算法信噪比门限优势越大，当归一化频偏为0.4时信噪比门限仍然保持在－2 dB以下，并且在保证－1 dB的信噪比门限前提下，估计范围达到理论值的99%。进一步增强处理后，信噪比门限还能降低约1.5 dB。该方法同时较好地满足了频率估计中的低信噪比门限和大估计范围两项要求。

4.1.7 一种宽范围高精度算法

由于现有前向载波频偏估计算法的估计精度和估计范围相互制约，文献［24］考虑针对Fitz算法进行改进，通过将相位展开来实现高精度宽范围的载波频偏估计。该算法首先对信号去除调制信息，然后求取自相关函数，并且进行多次迭代运算，在迭代中相位不会折叠，最后利用Fitz算法对消除了相位迭代的信号再次进行自相关函数加权运算，这将使得频偏估计范围由±1／（2MNT）拓展为±1／（2MT），并且估计精度没有损失。该算法在较低信噪比条件下仍然能获得良好性能。

4.2 频偏估计优化算法性能比较

表3给出了几种频偏估计优化算法性能之间的比较。

表3 频偏估计优化算法性能比较

5 结束语

针对短数据量的数字通信信号如何实现快速和精确频偏估计的方法展开了分析和研究。经典的测频方法归纳起来主要按照频域、时域及时－频分析方法进行分类，近些年出现的新算法主要是针对上述3类测频方法的优缺点，在此基础上根据具体的应用条件而提出的结合算法或改进算法。

随着通信技术的不断发展，突发通信模式的应用越来越广泛，突发信号的快速估计涉及范围广，研究难度大，国内外对这方面的研究时间也较长，但还有许多尚待解决的问题。首先，现在研究的大部分突发信号快速同步算法都是基于数据辅助，如利用时分系统的同步头数据对突发信号进行快速同步，而对无数据辅助的突发信号快速同步技术研究较少。为适应更多应用场合，无数据辅助条件下突发信号的快速估计的研究是有必要的。第二，在实际的应用中，飞机、导弹等用户的动态性较高，将会导致较大的多普勒频偏，因此，突发信号的载波频率估计算法需要有足够大的频率估计范围。为扩大突发信号快速估计技术在高动态性用户的适应范围，对大频偏突发信号的快速同步技术是必要而迫切的。第三，在传统的信息处理中，分析处理信息最常用的方法是傅里叶变换，但是它针对的是周期性平稳信号，依赖信号的全局信息，并不能反映信号的局部特征，故对分析非平稳信号不具有效性。然而，随着研究对象的复杂化、智能化，处理对象主要以非平稳信号为主。如何从强干扰的非平稳信号中有效提取具有某种特征的分量，显得尤为重要。目前对平稳信号的频率估计显得比较成熟，对非平稳信号的估计方法需要通过一定转换。如能将非平稳信号按照需要估计的特征成分的频率变化规律施加特定的转换，变成平稳信号加以估计，是一种比较理想的途径。第四，在近些年提出的一些新算法中，采用了矩形窗进行平滑，这只是相当于对各频率估计值进行了算术平均，可以考虑采用其他窗函数或寻找更合适的加权方式对各频率估计值进行平滑，这样可以实现在不影响其他性能的情况下提高估计准确性。

［1］Mengali U，D’ANDREA A N.Synchronization Techniques for Digital Receivers［M］.New York：Plenum Press， 1997：85－91.

［2］D’Andrea A N，Mengali U，Reggiannini R.The Modified Cramer-Rao Bound and its Application to Synchronization Problems［J］.IEEE Transactions on Communications，1994，42（2／3／4）：1391－1399.

［3］Rife D C，Vincent G A.Use of the Discrete Fourier Trans-form in the Measurement of Frequencies and Levels of Tones［J］.Bell Sys Tech J，1970，49（2）：197－228.

［4］Quinn B G.Estimating Frequency by Interpolation Using Fourier Coefficient［J］.IEEE Trans-SP，1994，42（5）：1264－1268.

［5］Quinn B G.Estimation of Frequency，Amplitude and Phase from the DFT of a Time Series［J］.IEEE Trans，1997，45（3）：814－817.

［6］叶展，张邦宁，潘小飞.基于FFT相位差的载波估计算法仿真与改进［J］.系统仿真学报，2012，24（11）：2414－2417.

［7］孔艳芳.一种载波频偏估计算法的实现［J］.电子测试，2011（2）：26－31.

［8］彭华.软件无线电中的盲接收技术研究［D］.郑州：中国人民解放军信息工程大学，2002：32－35.

［9］Fitz M P.Planar Filtered Techniques for Burst Mode Carrier Synchronization［J］.IEEE GLOBECOM，1991，12（1）：365－369.

［10］Luise M，Reggiannini R.Carrier Frequency Recovery in All-digital Modems for Burst-mode Transmissions［J］. IEEE Transactions on Communications，1995，43（2）：1169－1178.

［11］Mengali U，Morelli M.Data-aided Frequency Estimation for Burst Digital Transmission［J］.IEEE Transactions on Communications，1997，45（1）：23－25.

［12］石盛超，索龙龙，张卫同.基于自相关函数的前向频率估计方法综述［J］.电子质量，2012（12）：38－42.

［13］王利军.基于前导序列的突发通信载波同步算法［J］.无线电通信技术，2005，31（1）：4－5，31.

［14］Brown T，Wang M M.An Iterative Algorithm for Single-fre-quency Estimation［J］.IEEE Transactions on Signal Pro-cessing，2002，50（11）：2671－2682.

［15］帅涛，任前义，刘静，等.一种适用于大频偏和低信噪比条件的频率估计器研究［J］.宇航学报，2010，31（12）：2741－2745.

［16］Viteibi A.Nonlinear Estimation of PSK Modulated Carrier Phase Wide Application to Burst Digital Transmission［J］，IEEE Transactions on lnformation Theory 1983，29（4）：543－551.

［17］MohamedKN.SynchronizationinWireless Communication System［M］.Boston：Artech House，2004：219－234.

［18］刘良凯.突发信号的载波快速估计技术研究［D］.南京：中国人民解放军理工大学，2012：18－25.

［19］蒋 为.一种基于相关系数的频率估计算法［J］.微波学报，2012，28（2）：49－52.

［20］朱 磊，董 亮，刘树东.基于Quinn算法与改进的Rife算法的正弦信号频率估计［J］.大庆石油学院学报，2010，34（1）：98－101.

［21］Aboutanios E，Mulgrew B.Iterative Frequency Estimation by Interpolation on Fourier Coefficients［J］.IEEE Trans- actions on Signal Processing，2005，53（4）：1237－1242.

［22］Wang Hong-wei，Zhao Guo-qing.Improved Rife Algorithm for Frequency Estimation of Sinusoid Wave［J］.Signal Processing，2010，26（10）：1573－1576.

［23］周磊磊，罗炬锋，付耀先，等.低信噪比下基于自相关函数的频率估计方法［J］.华中科技大学学报（自然科学版），2014，42（4）：45－49.

［24］刘晓冬，陈卫东.一种宽范围高精度的载波频偏估计算法［J］.无线电工程，2014，44（3）：43－45.

Research on Feedforward Carrier Frequency Offset Estimation Algorithms in Burst Communication

YANG Han-zhu，LI Guang-xia，ZHAO Lu-wen，DU Feng
（Communication Engineering College，PLA University of Science and Technology，Nanjing Jiangsu 210007，China）

The burst communication，duo to its advantages like anti-jamming and low intercept probability，has become an important way of digital communication.The feedforward carrier frequency offset estimation has the advantages of fast estimation rate and no delay phenomenon，so it has been widely used in carrier synchronization of burst communication.Firstly，the paper introduces the Rife Algorithms and the Quinn Algorithms in frequency domain，the Fitz Algorithms，the L＆R Algorithms and the M＆M Algorithms in time domain，analyzes their basic ideas，then makes simulation of them and compares them with each other.Secondly，the paper introduces several latest algorithms，which have improved a lot，although，some limitations still exist in the practical application，in the hope of motivating the research in the field.

burst-mode communication；carrier synchronization；feedforward frequency offset estimation

TN911.7

A

1003－3114（2015）06－10－6

10.3969／j.issn.1003－3114.2015.06.03

杨晗竹，李广侠，赵陆文，等.突发信号前向频偏估计方法综述［J］.无线电通信技术，2015，41（6）：10－15，26.

2015－06－17

杨晗竹（1991―），女，硕士研究生，主要研究方向：卫星通信、卫星导航等。李广侠（1964―），男，教授，博士生导师，主要研究方向：卫星导航、卫星通信、卫星测控等。