ρ-混合序列完全矩收敛的精确渐进性

付宗魁，吴群英

（桂林理工大学理学院，广西桂林541004）

ρ-混合序列完全矩收敛的精确渐进性

付宗魁，吴群英

（桂林理工大学理学院，广西桂林541004）

设{Xn;n≥1}为正的严平稳ρ-混合随机变量序列，在适当的假设条件下，获得ρ-混合序列完全矩收敛的精确渐进性的一般形式.

ρ-混合序列；完全矩收敛；精确渐进性

0 引言及主要结果

定义1设{Xn;n≥1}是概率空间(Ω,F,P)的一列随机变量，集合=σ(Xi;1≤i≤n),=σ(Xi;i≥n).定义

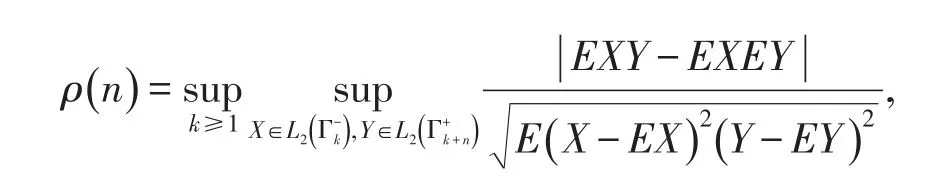
如果ρ(n)→0（n→∞），则称序列{Xn;n≥1}是ρ-混合的.

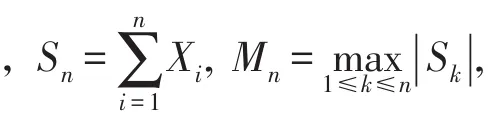
定理1设{Xn;n≥1}是均值为0的正严平稳-ρ混合序列，

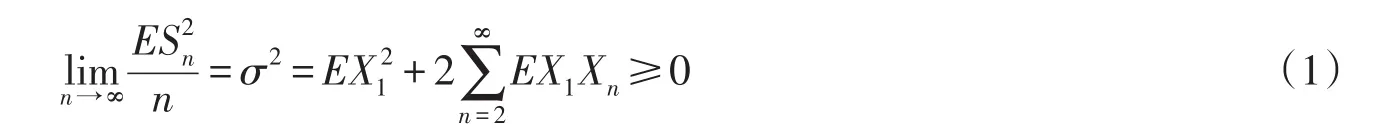
存在常量δ,r,q,满足δ＞-1,r＞0,r(δ+1)＞2和q＞r(δ+1),使得

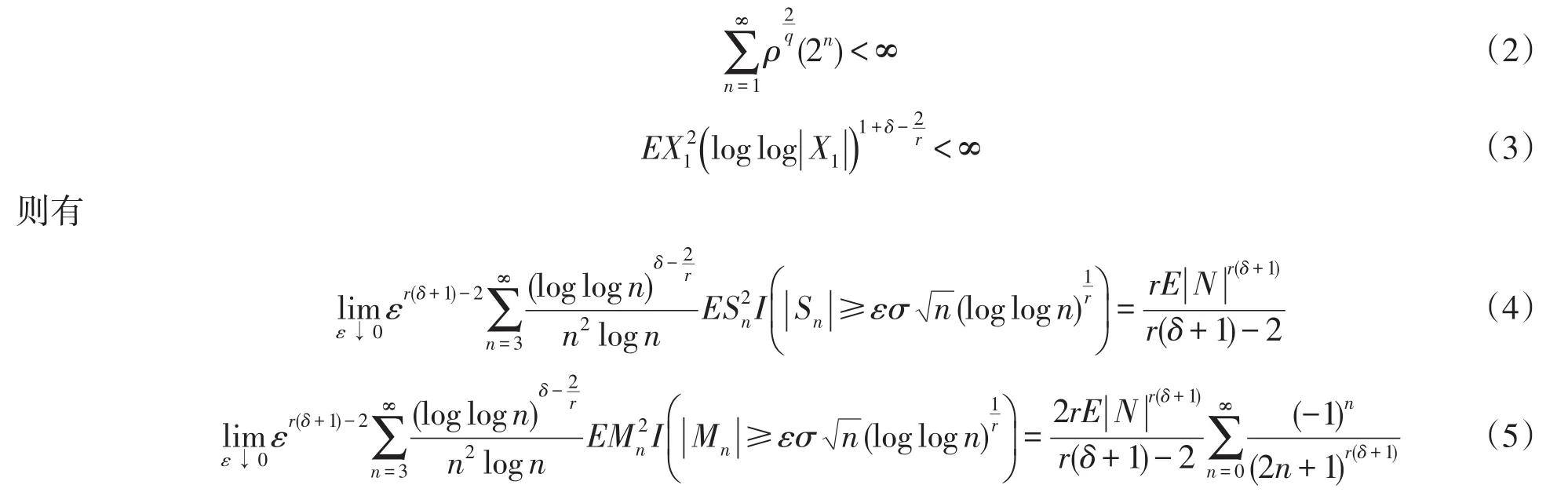
定理2设{Xn;n≥1}是均值为0的正严平稳-ρ混合序列，满足（1）式和（2）式，当EX时，则有

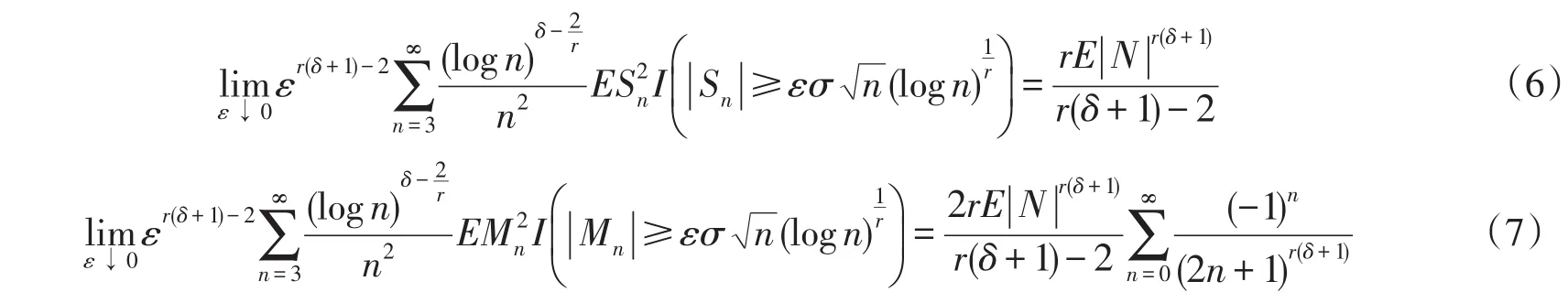
注1如果常量r,δ满足r=2和0＜δ≤1，则定理2就是文献［2］中的定理.

1 引理

先介绍证明中要用到的几个引理.

引理1［3-4］设{Xn;n≥1}为严平稳的ρ-混合序列，EX1=0，E＜∞,ρ(2n)＜∞,如果=E→∞(n→∞),则有→dN(0,1)，n→∞.而且，若σ＞0,则有Wn(t)⇒W(t),其中Wn(t)=S0≤t≤1,"⇒″表示在D[0,1]的弱收敛，利用Skorohod技术，则有M|W(t)|.

引理2［1］设{Xn;n≥1}为ρ-混合序列，EXn=0,Sn=.则对任意的q≥2,存在常数K=K(q,ρ(·))，使得对任意的x＞0和y＞0满足2nE|Xi|I(|Xi|≥y)≤x.则有

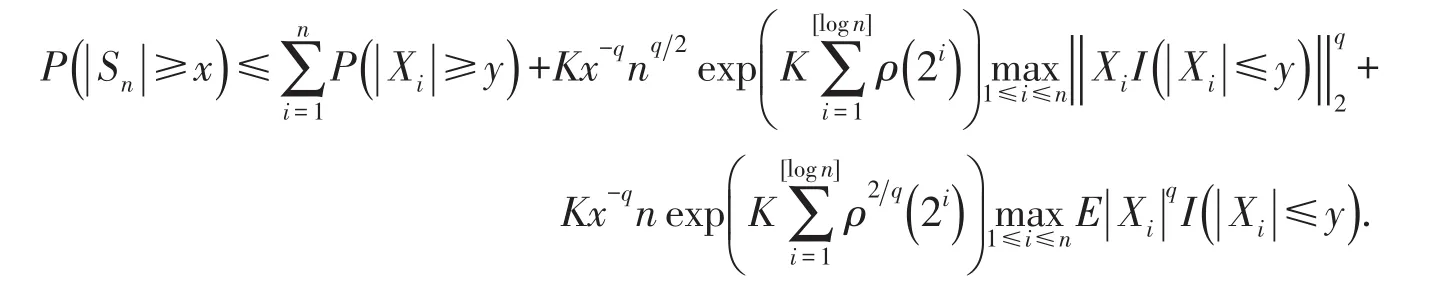
2 定理1的证明

不失一般性，不妨假设σ2=1，记Q(r,M,ε)=[exp(exp(M/εr))],其中r＞0,M＞4,0＜ε＜.先证明如下性质是成立的.

性质1在定理1的条件下，有：

性质2在定理1的条件下，有：

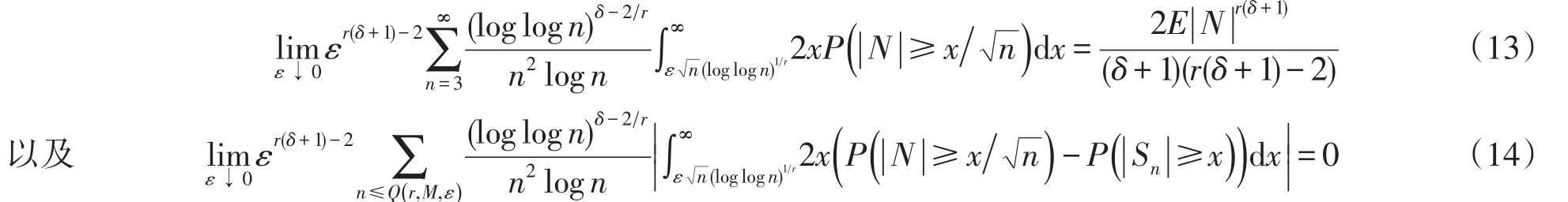
性质2的证明由文献［5，性质2.4］知式（13）成立.对式（14），则有

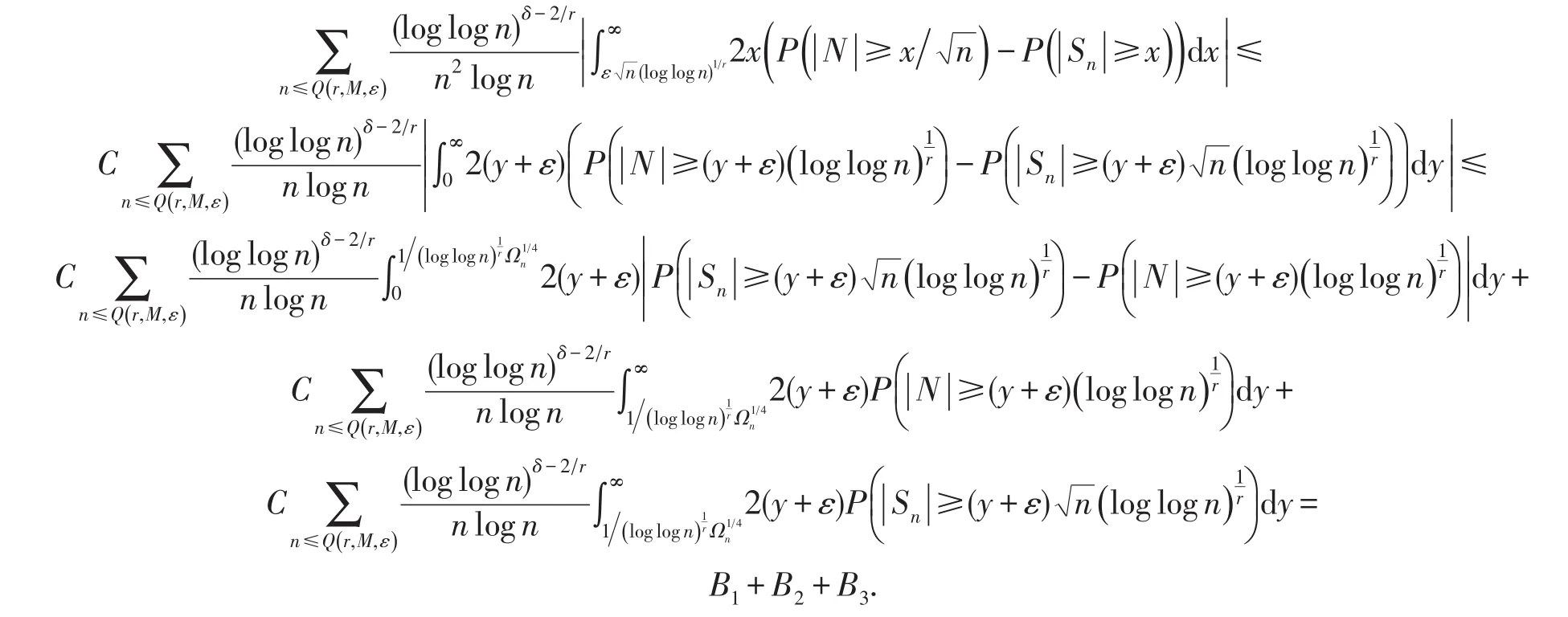
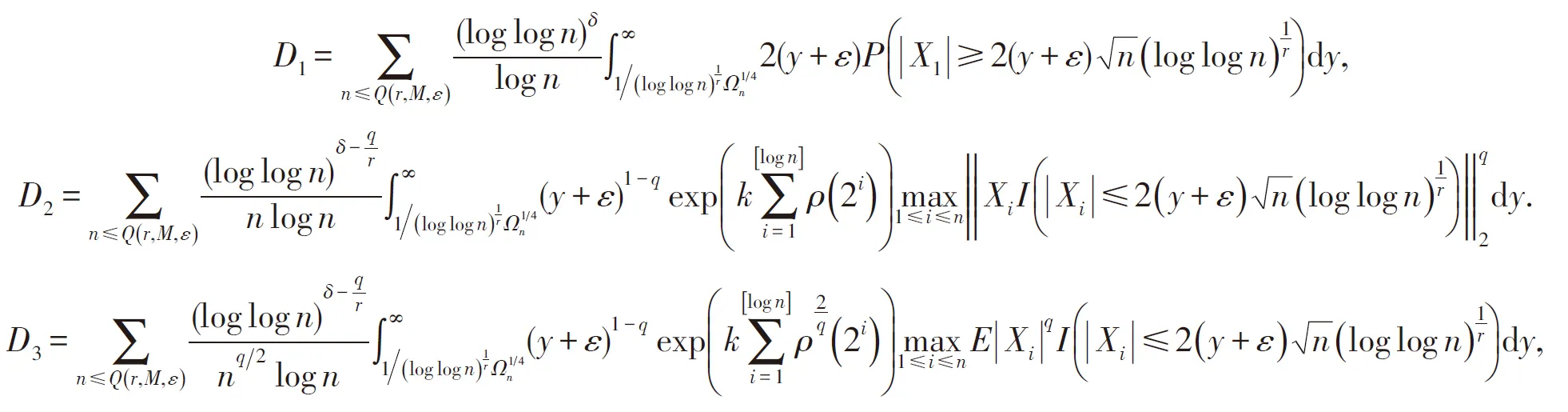
性质3在定理1的条件下，有：

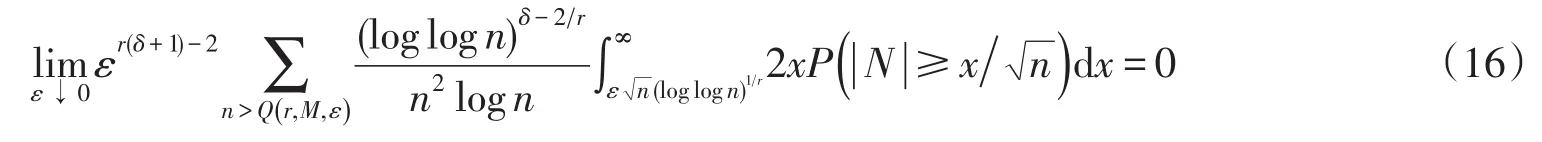
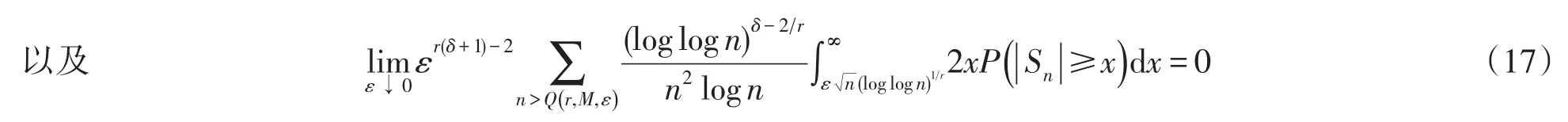
性质3的证明由文献［5，性质2.6］知式（16）成立.由引理2，则（17）式有

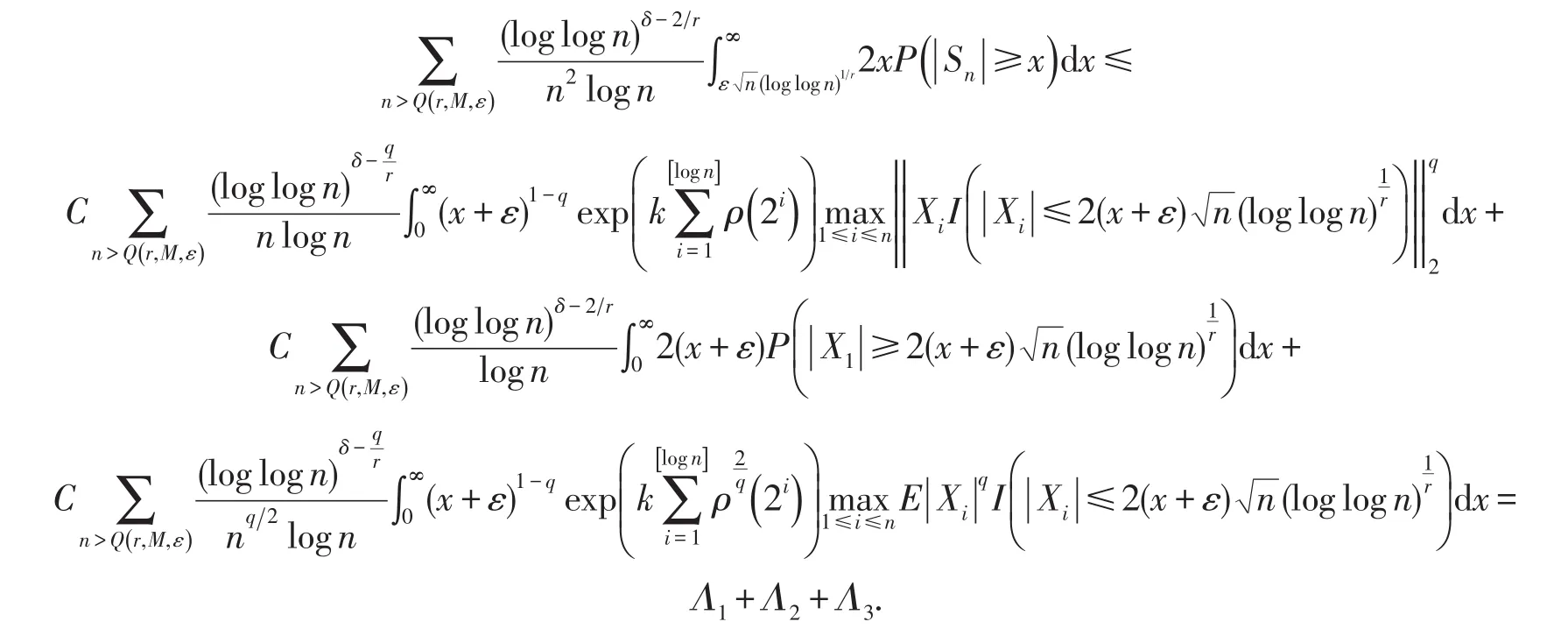
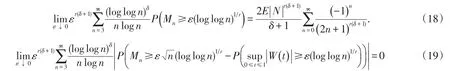
性质4的证明由文献［5，性质3.4］知（18）式成立，由引理1和Toeplitz’s引理知（19）式成立.

性质5在定理1的条件下，有：

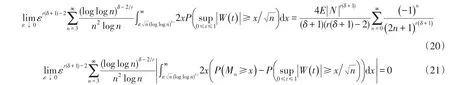
性质5的证明由文献［5，性质3.5］知式（20）成立.对于式（20），则有

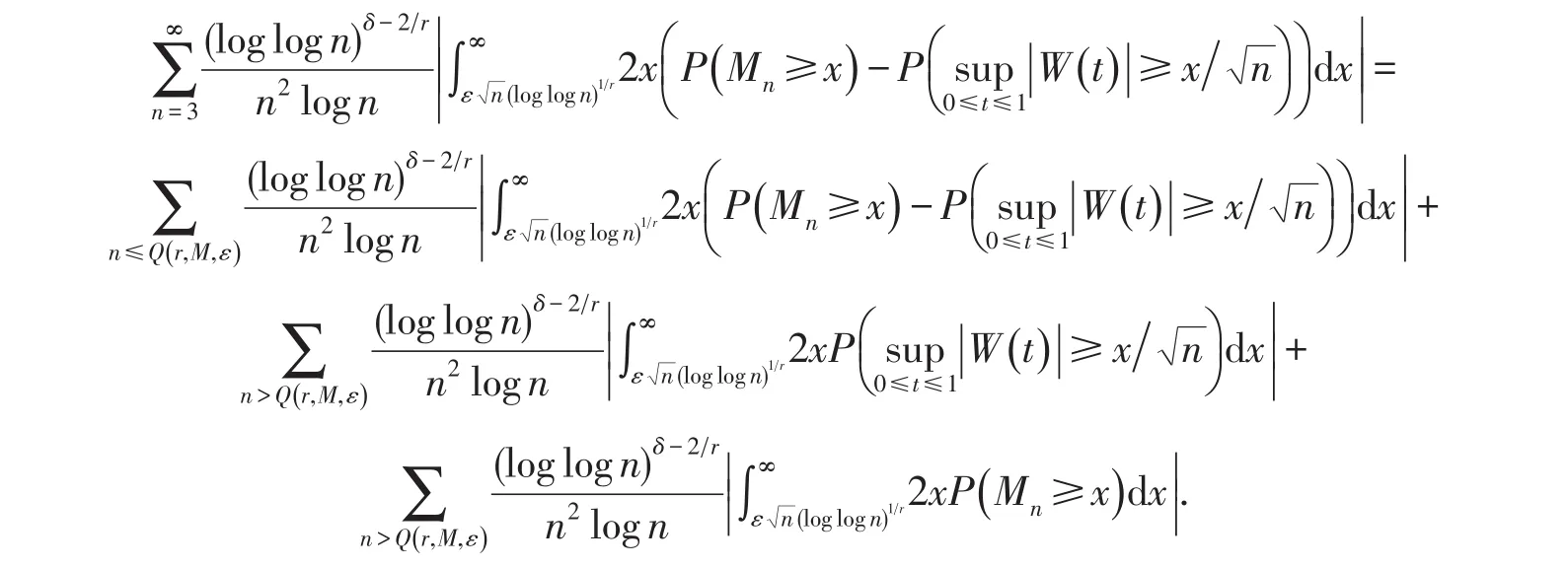
类似性质2的式（14）和性质3的证明知式（21）成立.

定理1的证明由矩运算，则式（4）等价于

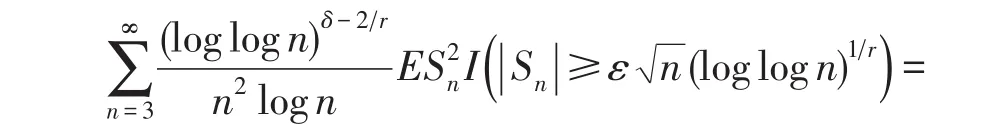
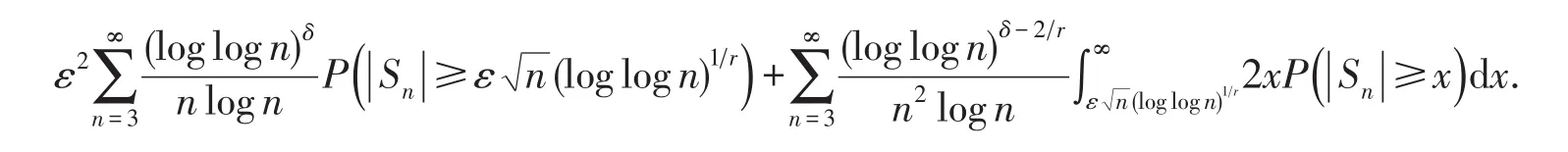
由性质1～3及三角不等式可证明（1）式成立.同样地，由矩运算、性质4和5及三角不等式可证明式（2）.

定理2的证明类似证明定理1的方法，故略.

［1］Shao Q M.Maximal inequalities for partial sums ofρ-mixing sequence［J］.Ann Probab，1995（23）：948-965.

［2］Zhao Y X.Precise rates in complete moment convergence forρ-mixing sequence［J］.J Math Anal Appl，2008，339:553-565.

［3］Ibragimov I A.A note on the central limit theorem for dependent sequences of random variables［J］.Probab Theory Appl，1975，20:134-139.

［4］Shao Q M.A remark on the invariance principle forρ-mixing sequence［J］.Chinese Ann Math Ser A，1988（9）:377-393.

［5］Zhao Y X.Asymptotic properties of the moment convergence for NA sequences［J］.Acta Mathematica Scientia，2014，34B（2）: 301-312.

［6］Zhang L X.Some limit results on the law of the iterated logarithm of NA sequences［J］.Acta Math Sinica Chin Ser，2004，47（3）: 541-552.

［7］Huang W，Jiang Y，Zhang L X.Precise asymptotics in the Baum-Katz and Davis laws of large numbers ofρ-mixing sequences［J］.Acta Math Sin Engl ser，2005，21:1057-1070.

（责任编辑 赵 燕）

Precise asymptotics in the complete moment convergence forρ-mixing sequences

FU Zongkui，WU Qunying
（College of Science，Guilin University of Technology，Guilin 541004，China）

Let{X,Xn;n≥1}be a strictly stationary sequence ofρ-mixing random variables，if some conditions were satisfied，we obtained some general results on complete moment convergence forρ-mixing sequences.

ρ-mixing random variables；complete moment convergence；precise asymptotics

O211.4

A

10.3969/j.issn.1000-2375.2015.05.006

1000-2375（2015）05-0431-07

2015-03-18

国家自然科学基金(11361019)、广西自然科学基金重点项目(2013GXNSFDA019001)和广西高校人才小高地建设创新团队资助计划（桂教人[2011]47号）资助

付宗魁（1990-），男，硕士生，E-mail:gut_fuzongkui@163.com