两种特殊图类直径的上界
庄 蔚
(厦门理工学院应用数学学院,福建厦门361024)
两种特殊图类直径的上界
庄 蔚
(厦门理工学院应用数学学院,福建厦门361024)
对边控制临界图与边控制极小图这两种特殊图类的直径进行了研究.给出了连通的k-EDC(k≥3)图的直径的一个上界,并给出了4-EDC图的直径的一个更好的上界及3-EDC图的直径的可达上界.同时,利用控制点临界图的已有的结果以及一个图的直径与其线图的直径间的关系,直接给出了连通的k-EDM图的直径的一个上界,进而给出了3-EDM图和4-EDM图的直径的可达上界.
边控制临界图;边控制极小图;直径
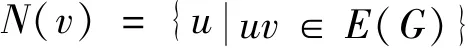
1 主要结论
根据边控制临界图与边控制极小图的定义,容易得到下列结论:
命题1 假设G为边控制临界图,uv∈E(G-),S为G+uv的最小边控制集,则有
1)uv∈S;
3)u,v两点在G中的关联边都不在S中;
4)G中没有孤立点.
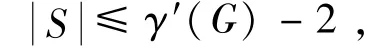
命题2假设G是边控制极小图,uv∈E(G),S是G-uv的最小边控制集,则
1)u,v两点的关联边都不在S中;
4)G中没有割点.
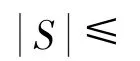
定理1如果G是一个连通的3-EDC图,那么diam(G)≤2.
由于完全二部图K3,3是一个3-EDC图,因此定理1给出的是一个上确界.下面将给出k-EDC图(k≥4)直径的一个上界:
定理2如果G是一个连通的k-EDC图,k≥4,那么diam(G)≤3k-6.
显然,定理2给出的上界并不是紧的,因此对于4-EDC图的直径,将给出一个改进的上界:
定理3如果G是一个连通的4-EDC图,那么diam(G)≤5.
在讨论边控制极小图的直径之前先引入几个概念.令G=(V,E)是一个简单图,S⊆V(G),如果对于任何一点v∈V(G)\S,在S中都有邻点,则称S为图G的一个控制集.在G的所有控制集中,点数最少的控制集称为最小控制集.最小控制集包含的点的数目称为G的控制数γ(G).若对于任意的点v∈V(G),都有γ(G-v)<γ(G),则称G是点控制临界图.
引理1[5]如果G是控制数为k的点控制临界图 (k≥2),则diam(G)≤2k-2.
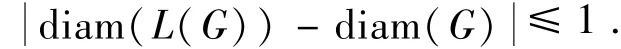
注意到,一个连通的k-EDM图的线图就是一个控制数为k的点控制临界图.因此从上面2个引理可以直接得到下面的结论.
定理4如果G是一个连通的k-EDM图,k≥2,那么diam(G)≤2k-1.
显然,定理4给出的上界并不是紧的,因此对于3-EDM和4-EDM图的直径,将分别给出2个改进的上界.
定理5如果G是一个连通的3-EDM图,那么diam(G)≤3.
定理6如果G是一个连通的4-EDM图,那么diam(G)≤5.
由于圈C7,C10分别是3-EDM图和4-EDM图,且直径分别为3和5,因此定理5和定理6给出的上界都是紧的.在下文中,由于定理1和定理3证明方法极为类似,且定理1证明过程与定理3相比更为简单,因此将只给出定理3的证明.同样的,由于定理5和定理6证明方法极为类似,且定理5证明过程与定理6相比更为简单,因此将只给出定理6的证明.
2 几个定理的证明
定理2的证明:用反证法,假设存在一个k-EDC图G′使得diam(G′)=t≥3k-5.必然存在a, b∈V(G′)使得的d(a,b)=t,t≥7.令P=ax1x2…xt-2xt-1b是a,b间的一条最短路.注意到x2xt-2∉E(G′),令S是G′+x2xt-2的最小边控制集.在E(P)中,{x1x2,x2x3,…,xt-3xt-2,xt-2xt-1}被x2xt-2控制,又因为P是a,b间的最短路,ax1和xt-1b分别由S\{x2xt-2}中的两条边控制.如果γ′(G′)=4,那么P中其余的边不可能被S中的边控制,否则a,b间将出现更短的路.如果γ′(G′)≥5,S中其余的k-4条边将控制P中其余的t-6条边.由于S\{x2xt-2}中的每条边所能控制的P中的边的数目不多于3条,于是有t-6≤3(k-4),即t≤3k-6,与之前的假设矛盾.因此结论成立.

情形1G[V5∪V6]是完全图.
情形2G[V5∪V6]不是完全图.
因此结论成立.

情形1t=7.
在G-x3x4中,令S={e1,e2,e3}是G-x3x4的一个最小边控制集.由于x3,x4的关联边都不在S中,x2x3必然被x2的某条关联边控制,不妨设为e1.显然,au与ax1至少有一条边不能被e1控制,不妨设为au.假设au被e2控制,则e3可以控制{x4x5,x5x6,x6b,bv}中的所有边,那么可以得到连接a, b两点的长度小于7的路,矛盾.
情形2t=6.
因为x1不是割点,必存在u1u2∈E(G),其中u1∈V1\{x1},u2∈V2.假设存在一条边s1s2∈E(G),其中s1∈V3\{x3},s2∈V4\{x4},考虑G-x1u1(如果x1u1∉E(G),可以考虑G-x2x3,证明过程类似),令S1={e1,e2,e3}是G-x1u1的最小边控制集.显然,x1,u1的关联边都不在S1中.由于s1s2,vb不可能被S1中的同一条边控制,因此假设s1s2,vb分别被e1,e2控制.注意到e3不能控制{ax1,au1,x1x2,u1u2}中的所有边,e1控制x1x2或u1u2.由于e3控制au1和ax1,e2控制{x3x4,x4x5, x5b,vb}中的所有边,于是有e2=x4b,矛盾.因此在G中不存在一条边s1s2使得s1∈V3\{x3},s2∈V4\{x4}.由于x3不是割点,在V3\{x3}中存在点s1′使得s1′在V4中有邻点,进一步的,这个邻点只能是x4.同理,在V4\{x4}中存在点s2′与x3相连.通过类似于前面的推导,同样可以得到矛盾.
因此diam(G)≤5.结论成立.
[1]MITCHELL S,HEDETNIEMI S T.Edge domination in trees[J].Congr Numer,1977,19:489-509.
[2]DUTTON R,KLOSTERMEYER W F.Edge dominating sets and vertex covers[J].Discuss Math Grpah Theory,2013,33:437-456.
[3]ESCOFFIER B,MONNOT J,PASCHOS V T.New results on polynomial inapproximability and fixed parameter approximability of edge dominating set[J].Theor Comput Syst,2015,56:330-346.
[4]XIAO M,NAGARNOCHI H.A refined exact algorithm for edge dominating set[J].Theor Comput Sci,2014,560:207-216.
[5]FULMAN J,HANSON D,MACGILLIVRAY G.Vertex domination-critical graphs[J].Networks,1995,25:41-43.
[6]KNOR M,NIEPEL L,SOLTES L.Centers in line graphs[J].Math Slovaca,1993,43:11-20.
Upper Bounds of the Diameters of Two Classes of Graphs
ZHUANG Wei
(School of Applied Mathematics,Xiamen University of Technology,Xiamen 361024,China)
In this paper,we study the problem about the diameter of edge domination critical graph and edge domination minimal graph.For k≥3,we obtain an upper bound of the diameter of connected k-EDC graph.Furthermore,we obtain a better upper bound of the diameter of 4-EDC graph and a sharp upper bound of the diameter of 3-EDC graph.Meanwhile,we use some results of domination vertex critical graph and the relationship between the diameter of a graph G and the diameter of the line graph L(G)of G to obtain an upper bound of the diameter of a connected k-EDM graph.Furthermore,we obtain the sharp upper bounds of the diameters of 3-EDM graph and 4-EDC graph.
edge domination critical graph;edge domination minimal graph;diameter
O157
A
1673-4432(2015)05-0080-04
(责任编辑 李 宁)
2015-06-26
2015-10-10
国家自然科学基金项目 (11301440);福建省自然科学基金项目 (2015J05017);厦门理工学院高层次人才项目 (YKJ12026R)
庄蔚(1983-),男,讲师,博士,研究方向为组合图论.E-mail:2012111002@xmut.edu.cn

