碳纳米梁受电压激励的非线性振动分析
杨志安,刘志伟
(1.唐山学院 唐山市结构与振动工程重点实验室,河北 唐山 063000;2.华北理工大学 机械工程学院,河北 唐山 063009)
碳纳米梁受电压激励的非线性振动分析
杨志安1,刘志伟2
(1.唐山学院 唐山市结构与振动工程重点实验室,河北 唐山 063000;2.华北理工大学 机械工程学院,河北 唐山 063009)
选取电荷、广义位移为电路耦合机电系统的广义坐标,得到系统的动能、势能、电能及耗散函数。根据经典的拉格朗日-麦克斯韦方程建立数学模型,得到的振动方程是弱非线性Duffing方程。应用多尺度法求得系统的主共振的幅频响应方程,并进行了数值计算,分析了不同的参数对共振的影响。随着碳纳米梁长度和交流电压幅值的增大,振幅和共振区增大;随着碳纳米梁与固定极板间距和阻尼系数的增大,振幅和共振区减小。
碳纳米梁;多尺度法;弱非线性;主共振
0 引言
碳纳米材料因本身具有的优越性越来越受到学者们的关注,并对它的特性和结构进行了广泛的研究。碳纳米材料具有弹性高、密度低、绝热性好及强度高等特殊性能,可以广泛应用于纳米器件、传感器和纳米机械等[1-3]。因此,研究碳纳米梁动力学特性很有意义[4]。
以前,学者们的研究仅局限于线性振动,但是碳纳米梁的应变在本质上是非线性的,越来越多的研究者已经意识到这点,并且开始对碳纳米梁的非线性行为进行研究。文献[5]采用多尺度法研究了共振微梁在电场中的非线性响应问题,并建立了微梁在静电驱动下的模型。文献[6]研究了NEMS静态驱动梁在直流、交流电压下静态和稳态的特性。文献[7]研究了双壁碳纳米管强迫振动,在主共振和二阶主共振条件下,两层的双壁碳纳米管振动频率相同。文献[8]研究了碳纳米管非线性振动和单壁碳纳米管自由振动的幅频响应曲线。文献[9]研究了双壁碳纳米管的随机振动和系统的幅频响应曲线。文献[10]分析了弯曲梁的非线性主共振及内部共振,并且研究了双倍分叉导致的混沌。目前尚未见研究碳纳米梁在电压激励下的非线性系统振动问题的报道。本文将研究碳纳米梁在电压激励下的非线性系统主共振的共振问题。
1 碳纳米梁受电压激励振动的动力学方程
图1为碳纳米梁受电压激励振动模型。两端固定、长度为L、半径为R的矩形截面梁,它与电极板通过电路连接,g表示电极板与梁的初始距离,碳纳米梁在电压的横向简谐激励下发生自由振动。

图1 碳纳米梁受电压激励振动模型
建立极板的坐标系,选横向位移u和电量q为广义坐标。
(1)

(2)

(3)

(4)
式中:u(x,t)为位移,A为截面面积,I为转动惯量,E为杨氏模量,ρ为质量密度,c为梁在粘性介质中的阻尼系数,N为梁的内部压力。
根据拉格朗日函数:

(5)
式中ε0为真空介电常数。
根据经典的拉格朗日-麦克斯韦方程有:

(6)
式中L代表拉格朗日函数,L=T+Wm-Π-We,即动能加磁能减去势能再减去电能。F代表电与机械的耗散函数之和。
当电路系统处于放电结束的瞬间,电容器极板电量q=0,此时耦合系统转化为纳梁振动系统,代入式(6)中,整理得:
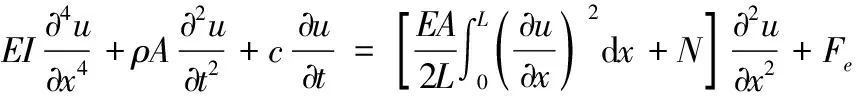
(7)

上述各式在经过哈密顿变分原理、伽辽金方法后,可以推出梁在电压作用下的数学模型及相应的微分方程。将式(7)偏微分方程转化为常微分方程,对于两端简支约束的纳米梁,将满足内力和位移边界条件的解取为如下形式:
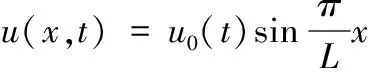
(8)
式中u0(t)为纳米梁中点处的位移。
将式(8)代入式(7)中,并采用伽辽金方法进行积分,得

(9)



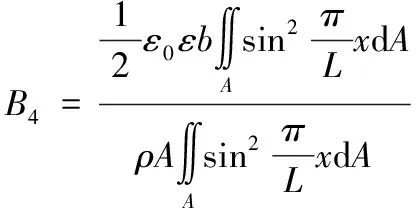
对(9)式进行无量纲化处理,得:

(10)

式(10)等号右边的非线性电场力可以由泰勒级数进行展开,得:

(11)
将式(11)代入到式(10)进一步简化得:
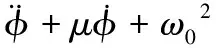
(12)

通过代入数据可知,非线性项系数的数量级比线性项系数的数量级小,可以确定静电驱动下碳纳米梁模型的数学方程式(12)为弱非线性方程。
2 2Ω=ω0主共振弱非线性理论分析
由图1推导的数学模型,可以得到纳米梁有阻尼的非线性振动方程。所谓主共振是指外激励频率2Ω接近派生系统固有频率ω0时的共振。如果系统是线性小阻尼系统,很小的激励幅值ζ2ζ3就能激起强烈的共振。这时阻尼力、外激励、非线性力与惯性力、线性力相比是小量,在它们前面冠以小参数ε,不考虑项cosΩτ,得到系统的方程为:

ζ2ζ3cos 2Ωτ]。
(13)
令2Ω=ω0+εσ,σ=o(1),代入式(13)中,得

(14)
研究一次近似解,采用两个时间尺度,故设
φ(τ)=φ0(T0,T1)+εφ1(T0,T1),
(15)
式中T0=τ,T1=εT0。
将式(15)代入到式(14)中,比较ε同次幂的系数,得到一组线性微分方程:
D02φ0+ω02φ0=0,
(16)
D02φ1+ω02φ1=-2D1D0φ0-μD0φ0-(ζ1-4ζ2ζ5)φ03+4ζ2ζ3cos(ω0+εσ)T0φ03+ζ2ζ3cos(ω0+εσ)T0。
(17)
式(16)的解为:

(18)

(19)


(20)
将式(20)由欧拉公式变化得:

(21)
将式(21)分离虚部、实部得:

(22)
令φ=σT1-β,由D1a=0,D1φ=0,且消去φ,得到幅频响应方程:
X6a6+X4a4+X2a2+X0=0。
(23)
式中:X6=9(ζ1-4ζ2ζ5)2,X4=-48ω0σ(ζ1-4ζ2ζ5),
X2=4(ω0μ)2+64(ω0σ)2,X0=4ζ22ζ32。
为了定量求解,给各参数赋值:

图2至图5为系统满足2Ω=ω0时主共振条件的幅频响应曲线,改变系统中的参数,纳米梁的振幅和振动区间能够发生明显的变化。图2是不同的纳米梁的长度对应的幅频响应曲线,可以看出增大梁的长度,幅值和共振区增加。图3是不同的交流电压幅值对应的幅频响应曲线,可以看出增大电压幅值,幅值和共振区增加。图4是不同的极板间距幅值对应的幅频响应曲线,可以看出增大梁与极板间距的幅值,幅值和共振区减小。图5是不同的阻尼对应的幅频响应曲线,可以看出增大阻尼的幅值,幅值和共振区减小。从图6可以看出一次近似解存在多频成分,一个周期内,振幅最值出现多个。而1次近似解比0次近似解的振幅大很多,所以时间历程算到1次近似解是很有必要的。

图2 不同的纳米梁长度对应的幅频响应曲线

图3 不同的交流电压幅值对应的幅频响应曲线

图4 不同的极板间距幅值对应的幅频响应曲线
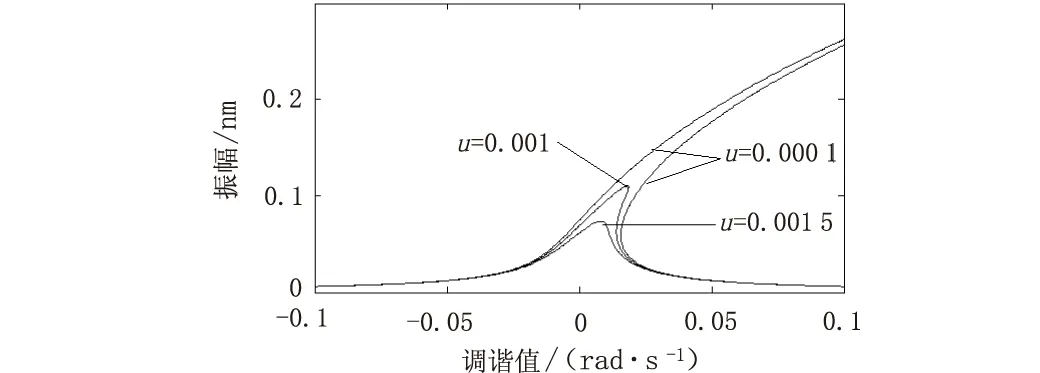
图5 不同的阻尼对应的幅频响应曲线
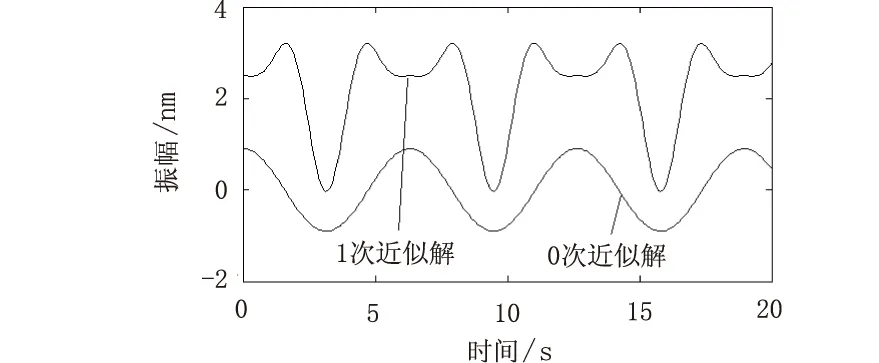
图6 时间响应曲线
3 结论
本文建立了碳纳米梁系统的动力学方程,通过代入参数比较线性项与非线性项的系数可知,碳纳米梁受电压激励非线性振动系统为弱非线性系统。数值计算结果分析显示:当碳纳米梁外激频率2ωf等于系统固有频率ω0时能激起系统的主共振。随着碳纳米梁长度和交流电压的增加,振幅和共振区增加;随着碳纳米梁阻尼系数和梁与固定极板的距离增大,振幅和共振区减小,一次近似解出现多个幅值,说明出现多频的成分。以上分析对于单壁碳纳米管参数的优化设计有参考价值。
[1] 郭永,巩雄,杨宏秀.纳米微粒的制备方法及其进展[J].化学通报,1996(3):1-4.
[2] 周双生,周根陶.纳米材料的制备及应用概况[J].化学世界,1997,38(8):399-401.
[3] 易文辉,郭焱.超微细粒子的制备及应用[J].化工新型材料,1996,24(11):7-9.
[4] 魏方芳.纳米材料的研究及应用[J].化学工程与装备,2007(3):38-40.
[5] Younis M I, Nayfeh A H. A study of the nonlinear response of a resonant microbeam to an electric actuation[J]. Nonlinear Dynamics,2003(31):91-117.
[6] Bhushan A, Inamdar M M, Pawaskar D N. Investigation of the internal stress effects on static and dynamic characteristics of an electrostatically actuated beam for MEMS and NEMS application[J]. Microsyst Technol,2011(17):1779-1789.
[7] Hajnayeb A, Khadem S E. Nonlinear vibration and stability analysis of a double-walled carbon nanotube under electrostatic actuation[J]. Journal of Sound and Vibration,2012(331):2443-2456.
[8] Fu Y M, Hong J W, Wang X Q. Analysis of nonlinear vibration for embedded carbon nanotubes[J]. J. Sound Vib,2006(296):746-756.
[9] Yan Y, Zhang L X, Wang W Q. Dynamical mode transitions of simply supported double-walled carbon nanotubes based on an elastic shell model[J]. J.Appl. Phys,2008(103):113523.
[10] Samir A Emam, Ali H Nayfeh. Nonlinear response of buckled beams to 1∶1 and 3∶1 internal resonances[J]. International Journal of Non-Linear Mechanics,2013(52):12-25.
(责任编校:夏玉玲)
An Analysis of Nonlinear Vibration of Electrically Actuated Carbon Nanobeam
YANG Zhi-an1, LIU Zhi-wei2
(1.Key Laboratory of Structure and Vibration of Tangshan City, Tangshan College, Tangshan 063000, China; 2.College of Mechanical Engineering,North China University of Science and Technology, Tangshan 063009, China)
Changing charge and generalized displacement as generalized coordinates of circuit coupling electromechanical system, kinetic energy, potential energy, electrical energy and dissipation function are obtained of a circuit coupling electromechanical system. According to Lagrange function,the weak nonlinear dynamic equation of carbon nanobeam system is established. By means of the multiple scale method of nonlinear vibration of primary resonance of the system are acquired and numerical calculation is carried out. Numerical analysis of the influence of different parameter is analyzed. With the increase of the length of the carbon nanobeam and ac voltage, the amplitude of the response curves and the resonance region enlarge; With the increase of the damping coefficient of the carbon nanobeam and spacing of the nanobeam and fixed plate, the amplitude of the response curves and the resonance region decrease.
carbon nanobeam; multiple scales method; weak nonlinear; primary resonance
O322
A
1672-349X(2015)03-0001-03
10.16160/j.cnki.tsxyxb.2015.03.001

