2002-2013年某市二氧化硫排放量的数学模型

孙翠先

(唐山学院 基础教学部，河北 唐山 063000)

2002-2013年某市二氧化硫排放量的数学模型

孙翠先

(唐山学院 基础教学部，河北 唐山 063000)

采集了某市2002-2013年二氧化硫排放总量的数据，借助于Matlab建立了一个四次多项式模型，并对误差进行了分析。

二氧化硫；排放量；数学模型

0 引言

空气中的二氧化硫来自于工业生产和居民生活的排放，年度内二氧化硫排放总量等于工业二氧化硫排放量与生活二氧化硫排放量之和。工业排放量指年度内企业在燃料燃烧和生产过程中排入大气的二氧化硫量；生活排放量指除工业生产以外的社会、经济活动及公共设施的经营活动中燃料燃烧所排放的二氧化硫量。二氧化硫可形成给人类带来灾难的酸雨，另外，二氧化硫对某些物品有腐蚀作用[1]。文献[2]对二氧化硫处理的物理、化学、生物方法进行了概述，文献[3]建立了二氧化硫总量的离散环境库兹涅茨曲线模型。本文将建立二氧化硫排放量的多项式模型，求出函数解析式，以描述变量之间的关系。随着计算机技术的不断发展，Matlab软件在建模过程中发挥了重要的作用，借助于Matlab可以方便、快捷、高效地解决数学建模中的问题[4]。

1 建立模型

1.1 数据来源

笔者从某市环境保护局官网环境质量状况公报中，采集了该市2002-2013年二氧化硫排放总量的数据，见表1。采集的这12组数据，跨越“十五”“十一五”和“十二五”三个阶段，具有代表性。

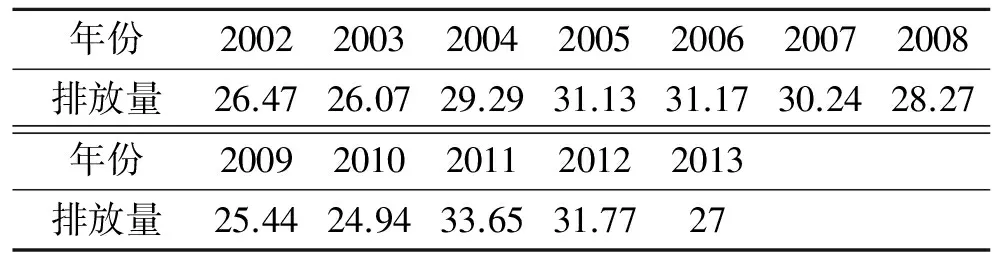
表1 2002-2013年某市二氧化硫排放总量 104t

1.2 符号引入

x表示年，取值为1-12，对应2002-2013年，y表示当年的二氧化硫排放总量。根据表1在Excel中画出折线图，如图1。函数关系设为y=f(x)。

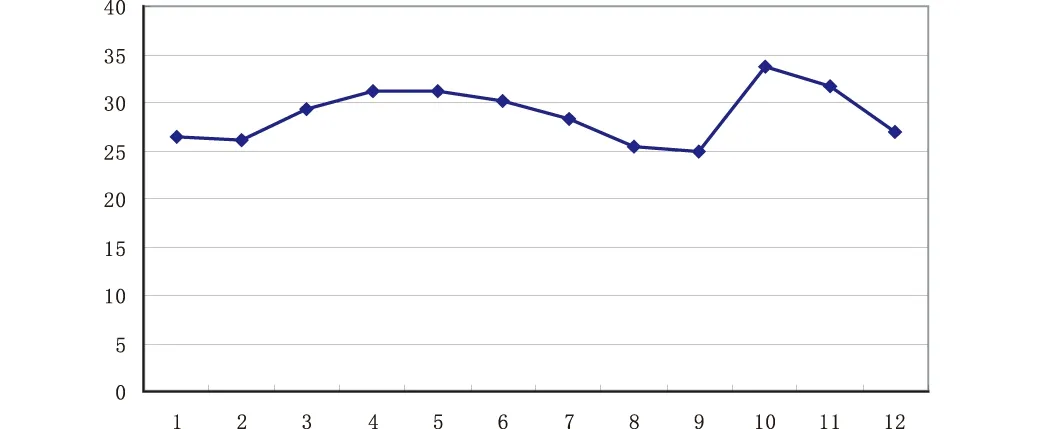
图1 12年间某市二氧化硫排放总量折线图

1.3 模型的选取和建立

由图1可以看出，曲线先单调增再单调减，然后再单调增再单调减，符合四次多项式的特点，故设函数关系为：

y=f(x)=a1x4+a2x3+a3x2+a4x+a5，

其中ai(i=1，2，…，5)为待定系数。

在Matlabr2007b的CommandWindow窗口中输入命令：

>>X=[1 2 3 4 5 6 7 8 9 10 11 12]；

>>Y=[26.47 26.07 29.29 31.13 31.17 30.24 28.27 25.44 24.94 33.65 31.77 27]；

>>[p，S]=polyfit(X，Y，4)

输出：

p=

-0.0104 0.2945 -2.8433 10.6791 16.6911

S=

R：[5x5double]

df：7

normr：8.1126

由此得模型y=f(x)的具体解析式为：

y=-0.0104x4+0.2945x3-2.8433x2+10.6791x+16.6911。

再输入命令：

>>Y=polyconf(p，X，S)

输出：

Y=

24.8110 28.8656 30.2474 30.0995 29.3151

28.5382 28.1630 28.3342 28.9469 29.6468 29.8298 28.6425

再输入命令：

plot(X，Y，'k+'，X，Y，'r')

输出：图2。

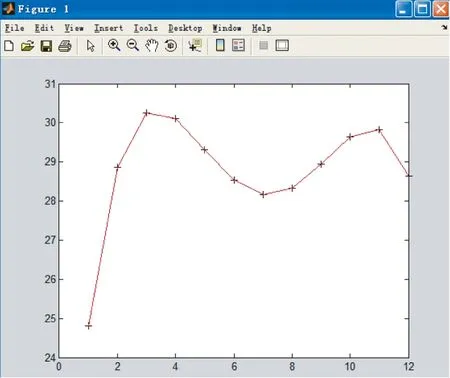
图2 估计值的折线

从图1和图2可以看出，曲线性质吻合，即模型选取正确。

2 模型分析

矩阵A表示试验值，B表示估计值。

输入：

A=[26.47 26.07 29.29 31.13 31.17 30.24 28.27 25.44 24.94 33.65 31.77 27]；

>>B=[24.8110 28.8656 30.2474 30.0995 29.3151 28.5382 28.1630 28.3342 28.9469 29.6468 29.8298 28.6425]；

>>A-B

输出：

ans=

1.6590 -2.7956 -0.9574 1.0305 1.8549 1.7018 0.1070 -2.8942 -4.0069 4.0032 1.9402

-1.6425

在Excel中画出误差ε=A-B，如图3所示，横坐标为x，纵坐标为ε。

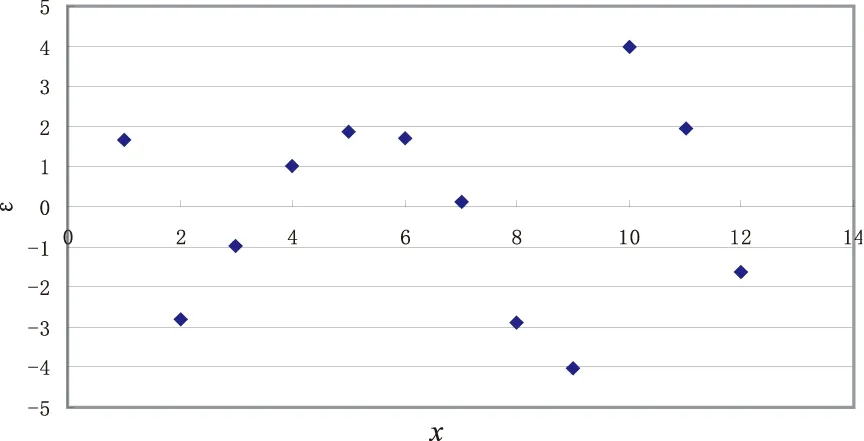
图3 误差散点

从图3可以看出，误差分布在水平线0的上下，分布均匀，表明建立的模型与实际数值拟合度高，客观地反映了12年间该城市二氧化硫排放总量的变化情况。

从图3还可以看出，第9，10号数据即2010，2011年的数据误差较大，将其列为异常值。产生异常值的原因有两个。一是2010，2011年的二氧化硫排放总量，分属于“十一五”“十二五”两个阶段。《“十一五”时期我国能源发展概况》中指出：五年来，无论是传统能源结构调整，还是清洁能源发展，都取得了重大进展。2011年是“十二五”的开局之年，随着经济发展方式的宏观调整，以及扩大内需等政策的出台，国民经济发展出现了良好势头。在此大背景下，该市“十一五”末“十二五”初的能源消耗出现波动是必然的，导致二氧化硫排放总量异常。二是建立的四次多项式函数，从数学角度讲该函数的曲线是连续光滑的，无不可导的点。而第9，10号数值正处于单调上升区间，与实际值产生较大误差的现象不可避免。

3 结语

控制二氧化硫排放量一直是各国环境保护工作的重点，我国从“十二五”开始探索利用二氧化硫排污权交易这一市场手段，以最小成本控制二氧化硫排放总量[5]，效果较好。

本文建立的二氧化硫排放总量的时间序列数学模型，为研究该市大气质量，加强环境保护提供了依据。

[1] 周琴.大气中二氧化硫的污染及防治对策[J].内蒙古环境保护，2002(9)：12-13.

[2] 洪哲.工业废气中二氧化硫处理方法研究综述[J].山东化工，2013(9)：39-42.

[3] 张永正，长青，李长青.离散型EKC模型与中国“十一五”期间二氧化硫减排目标分析[J].环境科学与管理，2009(2)：62-67.

[4] 赵静，但琦.数学建模与数学实验[M].2版.北京：高等教育出版社，2003：8.

[5] 姜超，苏良，唐方方.中国二氧化硫排污权交易机制研究[J].战略管理，2011(3)：77.

(责任编校：夏玉玲)

The Mathematical Model of Total Emission of SO2of a Certain City During 2002-2013

SUN Cui-xian

(Department of Fundamental Science Teaching， Tangshan College，Tangshan 063000，China)

The author of this paper created a four-degree polynomial model of the emission of SO2of a certain during 2002-2013 years， and then analysed the error with Matlab.

SO2； total quantity； MATLAB； teaching model

O141.4

A

1672-349X(2015)03-0014-02

10.16160/j.cnki.tsxyxb.2015.03.005