张峰水库溢洪道水力特性三维数值模拟

李建波,李 礼

(山西省水利水电勘测设计研究院,太原 030024)

张峰水库溢洪道水力特性三维数值模拟

李建波,李 礼

(山西省水利水电勘测设计研究院,太原 030024)

以张峰水库为例建立了溢洪道三维结构模型,采用结构网格及混合网格技术对模型进行了离散,并利用标准k-ε湍流模型、SIMPLE算法及VOF法对溢洪道流场进行了三维数值模拟。结果表明,溢洪道过流能力、水面线及流速分布与实测值吻合良好;溢洪道底板压强分布合理,水流空化数满足设计要求,溢洪道体型设计合理可靠。以物理试验验证数值模拟,使得计算结果真实、可信,进而详细地分析了溢洪道的压强特性及水流空化数,对同类工程的优化设计有一定的参考作用。

溢洪道;水力特性;数值模拟;VOF模型;水流空化数

溢洪道是水库枢纽的重要组成部分,它发挥着宣泄洪水,保护工程的重要作用,直接影响到大坝的安全运行[1]。目前国内学者为了使溢洪道建筑物的设计合理、安全、可靠,通常以物理模型试验和数值模拟技术对其进行分析研究。笔者在物理模型试验的基础上,对张峰水库溢洪道的泄流能力、水面线及流速分布进行三维数值模拟并验证,进而分析溢洪道底板的压强分布及水流空化数特性,确定了溢洪道设计参数,对同类工程的优化设计具有一定的参考作用。

1 工程概况

张峰水库位于山西省沁水县张峰村的沁河上,水库总库容为3.94×108m3,是一座防洪、供水、发电等综合利用的大型水库工程[2]。其枢纽包括大坝、溢洪道、渠首输水泵站、渠首电站等水工建筑物。其中,溢洪道由引渠段、闸室段、泄槽段、挑流段及尾水渠五部分组成。引渠段为喇叭口直墙段,向上游呈扩散布置;闸室段为无底坎宽顶堰,设4孔闸门,每孔净宽12 m,闸底高程为747.20 m。泄槽净宽55.5 m,长度为129.126 m,桩号0+034.00—桩号0+049.392采用WES曲线y=0.013x2;挑流鼻坎坎长18.0 m,反弧半径20 m,挑角28°。

2 数值模拟

2.1 控制方程

在水库上、下游水位已知的情况下,溢洪道恒定流动属于不可压缩的水流流动问题,笔者采用N-S方程描述离散方程,并利用标准k-ε双方程湍流模型求解。本次数值计算不考虑热能交换,则方程组不包含能量方程。连续方程、k方程、ε方程、动量方程和多相体积分数aa方程[3]分别如下。

连续方程:

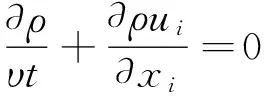
k方程:

ε方程:

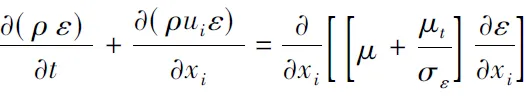
动量方程:

式中:t为时间;指标i=1,2,3;j为求和下标;ui和xi分别为速度分量和坐标分量,{ui=u,v,w},{xi=x,y,z};μ和ρ分别为分子粘性系数和密度;μt为紊流粘性系数;p为修正的压力。

为了精确地求解自由水面线,在标准k-ε湍流模型中引入求解自由水面线的流体体积分数方法(VOF法)。假设用φw表示水的体积分数,则空气的体积分数φa可表示为:

φa=1-φw.

在每个离散单元内,水的体积分数存在3种情况,即φw=0,1或介于0与1之间,分别对应空气、水和水气混合界面3种情况。水气混合界面则通过下面的连续方程来求解:

根据求解水的体积分数φw值即可确定自由水面线的位置。

2.2 计算区域与网格划分

依据溢洪道结构设计图及模型试验布置,按照原型尺寸建立了三维计算模型,包括库区、引渠、闸室、泄洪槽、挑流坎和退水渠六个部分。计算区域长477.5 m,宽116.4 m,高84.9 m,体型较大,结构复杂。为了减小计算时间,并满足计算精度的要求,将模型按照结构组成划分区域。库区、泄洪槽、退水渠为规则区域,采用六面体网格;闸室、挑流坎为不规则区域,采用混合网格,并对挑流坎进行了网格局部加密,如图1所示。网格单元大小在0.3 m～1.4 m之间,网格数量约为1.74×106个。

图1 计算区域网格划分图

2.3 数值解法

离散体的控制方程组可写成以下通用形式:

式中：Sφ为控制方程的源项;φ为通用变量,如湍动能、耗散率、速度等;τφ为通用变量φ的扩散系数。计算采用修正的Simple算法解决速度与压力耦合问题,并且采用高阶迎风离散格式处理数值扩散问题。以水流进、出口质量差值作为判断计算是否完成的依据,当计算精度小于3‰时,认为本次计算已经收敛。

2.4 边界条件

1) 进口边界。溢洪道计算模型的进口边界条件可分为空气进口和水流进口,空气进口选用压力边界条件,压力值为一个大气压。在水库进口水位已知的情况下,水流进口则选用自定义的压力边界条件。

2) 出口边界。出口边界条件同样分为空气出口和水流出口,空气出口为一个大气压,水流出口设定为下游水位。

3) 固壁边界。溢洪坝底板及侧壁均为固壁边界,选用无滑移边界条件,近壁区域采用壁面函数传递流场信息。

3 结果分析

依据上述计算方法及边界条件,选择校核工况(p=0.05%,洪水位762.63 m)对计算模型进行数值模拟,得到整个流场信息,依次分析溢洪道的泄流能力、水面线、典型断面流速分布、底板压强分布及水流空化数特性等水力参数。由图2溢洪道水流流态三维效果图可以看出,水流和大气分界比较明显,水流流线光滑、平顺,分布均匀、对称;流线经过挑坎,均匀地挑向下游;在引渠、闸室及挑流坎等部位,未出现漩流等不良流态。表明本文采用的计算方法是可行的。

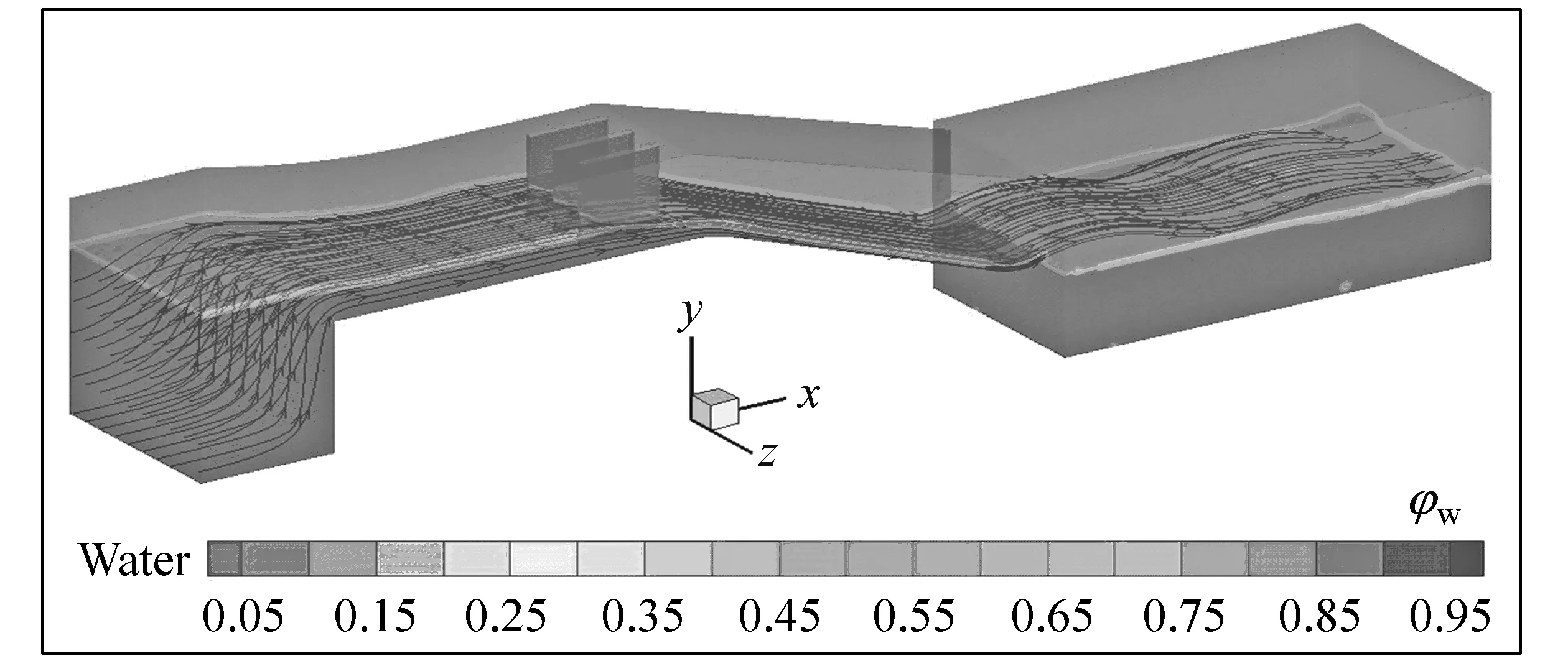
图2 溢洪道水流流态三维效果图

3.1 泄流能力

首先,计算了校核水位下溢洪道泄洪流量与模型实测值比较,对比情况如表1所示。由表1可见,在校核工况下,实测的泄洪流量为4 494.00 m3/s,计算得到的泄洪流量为4 582.19 m3/s,计算值比实测值大1.96%,与文献[4]结论一致。导致误差的原因首先可能是物理模型制作中WES曲线存在缩尺效应而造成的;其次为减少数值模拟的计算量,设置进口断面至溢流堰距离较近,溢流堰的堰上水头增大,使得计算流量偏大;再次，模型试验受到场地限制,出现水汽蒸发、水流飞溅等现象,导致实测泄洪流量偏小;模型试验采用量水堰只测得泄水流量,而数值计算的泄量包括空气流量,也是导致误差原因之一。但总体来说,两者吻合良好,计算结果可信。

表1 溢洪道泄流能力比较

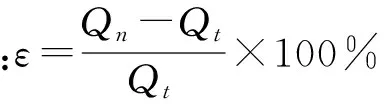
3.2 水面线

模型试验测量了溢洪道底板中心线上水面线沿程分布[5],数值模拟也提取了水气交界面内掺气浓度50%的水面线与实测值对比,如图3所示。图中，引渠段及闸室段内三个典型断面(桩号0-035.00，桩号0+000.00，桩号0+034.00)的计算水深分别为15.01，12.98，6.67 m,泄槽直线段及挑流段内的计算水深为3 m左右。表明在引渠段及闸室段内水位沿程逐渐降低,进入泄槽段后水位趋于平稳,桩号0-035.00断面实测水深为14.98 m,计算水深为15.01 m,计算值大于实测值0.18%。桩号0+124.19断面实测水深为3.16 m,计算水深为3.09 m,计算值小于实测值2.07%。两者差别的原因首先可能是数值计算网格单元尺寸略大,水气交界面存在一定厚度,水面线的提取形成偏差；其次，模型试验水流流速较大,水面波动比较明显,干扰了水面线的测量,使得实测值不够精确。为了证明水位计算值与实测值的吻合度,比较了溢洪道底板中心线上水位的计算值与试验值(如图4所示)。由图可知,横坐标为水位试验值,纵坐标为水位计算值,散点基本分布在线性回归方程y=0.997x+2.360上,其相关系数R为1.0,大于0.8。表明计算值与实测值基本一致,两者吻合良好。

分析闸室段内横向水位可知,水流在闸室进口断面(桩号0+000.00)受到闸墩阻水影响,导致横向水位波动较大,最大水位相差1.47 m;两侧闸孔内水位略高于中间两闸孔水位,并在每个闸孔内水位呈边侧高、中线低分布;水流流进闸室内,水位逐渐趋于平稳,水位差亦逐渐变小(桩号0+025.00断面,水位相差0.43 m)。但两侧闸孔内水位同样略高于中间两闸孔水位,其原因可能是引渠断面收缩及闸墩阻水、分流作用的影响;水流流出闸室出口断面(桩号0+034.00),立刻形成小规格的菱状水波,横向水位差值增大，并且在每个闸孔内水位呈边侧低、中线高分布。上述闸室段横向水位分析与模型试验测量结果是一致的。

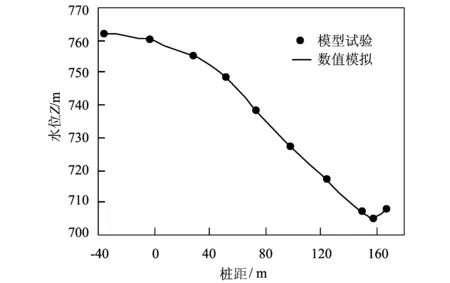
图3 溢洪道底板中心线水面线分布

图4 溢洪道底板中心线水位计算值与试验值比较

3.3 断面流速分布

模型试验在溢洪道控制段面布置了流速测量断面,数值模型也提取了相应断面的流速值并与实测数据进行对比。由图5溢洪道内其中两个典型断面垂线流速分布情况可以看出，沿水深方向,桩号0+034.00断面模型实测的水流自近底流速12.71 m/s增大至表层流速13.61 m/s,数值计算得到的流速约为13.12 m/s。同理,桩号0+166.00断面实测流速约为28.87 m/s,计算水流流速为27.05 m/s～28.72 m/s。由此表明,溢洪道内沿水深方向水流流速分布比较均匀；桩号0+034.00断面,实测断面平均流速为13.19 m/s,数值计算得到断面平均流速为13.12 m/s,两者相差0.56%。同理,桩号0+166.00断面实测断面平均流速为28.87 m/s,计算断面平均流速为27.96 m/s,两者相差3.15%。表明,溢洪道内顺水流方向断面平均流速沿程逐渐增大。鉴于上述分析,数值计算的流速分布趋势不仅与模型试验的流速分布趋势一致,且数值大小也与实测值吻合良好。

综上所述,溢洪道过流能力、水面线及流速分布与模型试验结果吻合良好,说明计算结果是可信的。

图5 典型断面中垂线流速分布

3.4 底板压强分布

图6给出了溢洪道底板中心线上压强分布所示,横坐标为桩号,纵坐标为压力水头。由图可见,溢洪道底板压力水头均在2.14 m以上,未出现负压;泄槽段压强分布基本上光滑平顺，表明溢洪道底板压强分布合理,溢洪道体型设计合理可靠;泄槽直线段内的压强分布线逐渐平行于底板,压力水头在2.57～3.83 m范围内变化,表明泄槽内水流较为平稳;渥奇面桩号0+045.67断面,出现了压强最小值,压力水头约2.14 m;反弧段桩号0+159.69断面,出现了压强最大值,压力水头约15.69 m。渥奇面和反弧段底板内出现压强极值,其原因可能是水流受到离心力作用,产生的动水压强导致静水压强发生较大变化。

图6 溢洪道底板中心线压强分布

3.5 水流空化数分布

空化、空蚀是泄水建筑物中最常见的水力学问题,具有破坏深度大、面积广、维修费用高及用时长等危害,严重影响泄水建筑物的安全运行[6]。学者通常采用水流空化数来判别空化状态和破坏强度,计算公式[7]如下，

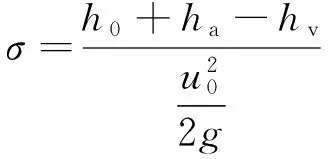
(1)

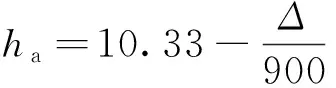
(2)

式中:σ为水流空化数;h0为参考断面压力水头,m;ha为建筑物所在地区的大气压力水柱,取9.44 m;hv为水的汽化压力水柱,取0.24 m;u0为参考断面平均流速,m/s;Δ为当地海拔高度,取800 m。

图7 溢洪道水流空化数沿程分布

笔者前面分析了溢洪道内典型断面平均流速及底板静水压力分布,在此基础上应用式(1)、(2),计算得到溢洪道内水流空化数沿程分布情况,如图7所示。由图可以看出，在泄槽段内,水流空化数从起始断面(桩号0+034.00)的最大值1.91逐渐减小至最小值0.31(桩号0+145.43断面)。而水流进入到挑流段后,空化数从0.31逐渐增大至0.62(桩号0+156.70断面)后又减小至0.38(桩号0+165.12断面)。因此,水流空化数在泄槽段内沿程逐渐减小,挑流段内呈先增大后减小分布；在桩号0+145.43断面,位于挑流坎始端附近,出现了水流空化数最小值0.31,其结论与文献[8]一致；水流空化数均在0.3以上,溢洪道能够满足设计要求,施工中应严格控制过流面不平整度,防止气蚀发生。

4 结论

1) 通过数值模拟分析溢洪道泄槽段内水流平稳,压强分布光滑平顺;渥奇面和反弧段内分别出现了压强极小值和压强极大值,底板压强未出现负压;泄槽段内水流空化数沿程逐渐减小,挑流段内水流空化数呈先增大后减小分布;水流空化数均在0.3以上,表明溢洪道体型设计合理可靠,满足工程运行要求。

2) 数值模拟得到的溢洪道过流能力、水面线及流速分布与模型试验结果吻合良好,表明三维数值模拟分析方法正确,计算结果可信,能够广泛应用于工程实例,对同类工程有一定的参考价值。

[1] 何照青,祁永斐,李卫鹏.基于VOF模型的阿拉沟溢洪道流场数值模拟[J].水资源与水工程学报,2013,24(2):170-173.

[2] 苏冬阳.张峰水库溢洪道泄流能力分析[J].山西水利科技,2008,168(2):8-9.

[3] 崔润.溢流表孔门槽水力特性三维数值模拟研究[J].人民长江,2013,44(7):67-70.

[4] 牛坤,把多铎,吴小平.天生桥水电站溢洪道三维数值模拟[J].水电能源科学,2011,29(2):62-64.

[5] 许鸿飞.山西省张峰水库溢洪道水工模型试验报告[R].山西省水利科学研究院,2004,8:32-33.

[6] 吴建华.掺气减蚀技术及其研究[C]∥吴有生，周如萍，颜开，等.第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源诞辰110周年纪念大会文集.北京：海洋出版社，2012:87-94.

[7] 赵业彬,徐艺绯,骆少泽.某水电站溢流坝陡槽高速泄流掺气减蚀试验研究[J].水电能源科学,2012,30(9):82-84.

[8] 范世平,刘伟明,石建军.柏叶口水库溢洪道底板压力分布及抗空蚀性能分析[J].水力水电技术,2010,41:37-40.

(编辑：朱 倩)

Three-dimensional Numerical Simulation on the HydraulicProperties of the Spillway of Zhangfeng Reservior

LI Jianbo,LI Li

(ShanxiHydroelectricityInvestigationandDesignInstitute,Taiyuan030024，China)

In this paper,three dimension frame model of the spillway is established to the case of Zhangfeng Reservior.The model is discretized with structure grids and hybrid grids.And the flow field of the spillway is simulated by 3-D numerical model,in which a k-ε turbulent model,SIMPLE Algorithm and volume of fluid (VOF) method are used.The results show a good agreement with the measured value about discharge capacity,water surface and the velocity distribution of the spillway.There is a reasonable distribution of the pressure on the bottom,and the flow cavitation number satisfies the design requirements.The results of numerical simulation were proved to be true and credible by the measured values.Then,a detailed analysis was given on the pressure characteristics and the flow cavitation number of the spillway,which is very useful for the optimization design of similar projects.

spillway;hydraulic propertie;numerical simulation;VOF model;flow cavitation number

1007-9432(2015)06-0775-05

2015-03-09

李建波(1970-),男，山西永济人，高级工程师，主要从事水工设计方向的研究，(Tel)13935149903

TV TV651.1

A

10.16355/j.cnki.issn1007-9432tyut.2015.06.025