基于无源性的塔机模糊神经网络防摆控制

王雨婷，陈志梅，邵雪卷

(太原科技大学电子信息工程学院，太原 030024)

基于无源性的塔机模糊神经网络防摆控制

王雨婷，陈志梅，邵雪卷

(太原科技大学电子信息工程学院，太原 030024)

针对塔式起重机的防摆控制问题，提出了一种基于无源性的模糊神经网络控制方法。通过建立Lyapunov能量函数，分析了系统的无源特性，在此基础上采用模糊控制并依靠神经网络对隶属函数进行学习，不需要依赖系统精确的数学模型，实现了塔式起重机小车的定位和负载的防摆，提高了系统的鲁棒性。仿真结果表明该方法的有效性和可行性。

塔式起重机;无源性;模糊神经网络;定位;防摆

塔式起重机广泛应用于货物的装卸，针对塔式起重机定位和负载摆动问题，许多学者进行了相关的研究。文献［1-2］采用轨迹跟踪的方法提出了一种防摇策略。Dominik Schindele等［3］人采用了最优控制的方法。文献［4-5］等人设计了非线性PID控制器，实现了起重机定位和负载的防摆。上述这些研究方法大多依赖理想的环境以及精确的数学模型。文献［6-7］应用了模糊控制理论来设计控制器，根据人工经验设计了模糊规则，这种控制方法不依赖精确的数学模型，能够很好的达到防摆的目的。但模糊控制的隶属函数对系统性能有很大影响，其幅度越宽控制精度越低，常出现不必要的重叠也会使得控制效果变差。

无源控制作为一种较新的控制方法，其物理背景和Lyapunov函数密切相关，且是从系统的能量属性研究系统的控制问题，其无功力可以简化控制器的设计。文献［8］应用分数阶与无源理论相结合设计了一种无源分数阶控制器，这种控制方法使系统具有良好的动态性能和较强的鲁棒性。

为了能在复杂的环境中更好地实现起重机定位和防摆控制，本文提出了一种基于无源性的模糊神经网络控制方法。分析系统的无源性，通过神经网络对隶属函数进行学习，减轻模糊控制规则对人工经验的依赖性，采用模糊神经网络控制器可以很好的实现塔式起重机小车的定位和负载的防摆，并提高系统的鲁棒性。

1 塔式起重机数学模型的建立

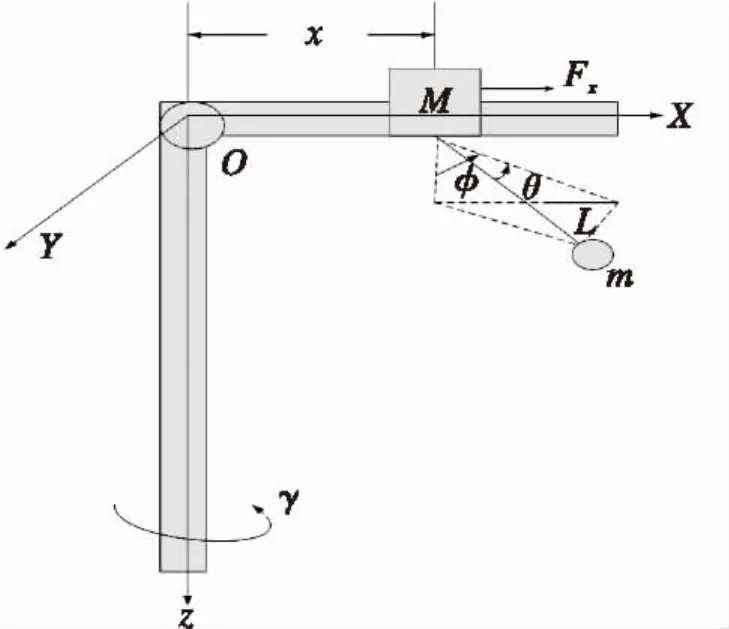
图1 塔式起重机模型Fig.1 The model of tower crane

图1所示为塔式起重机的简化模型结构［9］。

其中:x为臂架小车与塔机中心轴线的垂直距离;M为小车的质量;m为负载的质量;L为绳长;γ为负载旋转的角位移;J0为转动惯量;φ为绳长在XZ平面上的投影与Z轴的夹角，θ为绳长在XZ平面上的投影与绳长方向的夹角;Fx为沿X方向上小车所受的作用力;Tγ为回转转矩。

忽略吊绳的质量与弹性，绳长L固定不变;把负载看作是一个质点;各传动机构间的摩擦忽略不计。以小车位置为零势能点，由模型可求得系统动能和势能分别为:

2 控制器设计

2.1 无源性分析

设系统的能量函数为:

无源控制器的设计仅仅使用了反馈控制，不能很好地达到定位和防摆的目的。因此采用模糊神经网络分别对小车位移和负载摆角进行控制，神经网络对模糊控制隶属函数进行学习可以避免对人工经验的依赖，增加系统的自适应能力。

2.2 模糊神经网络控制器设计

(1)模糊神经网络控制器结构［10］如图2所示。

模糊神经网络控制器由输入层、模糊化层、规则层和输出层组成。由于式(3)和(5)，式(4)和(6)分别体现了塔式起重机的变幅运动和回转运动，所以首先设定x，φ为模糊神经网络系统的输入矢量，y为输出矢量;然后进行模糊规则推理:分别为对应的模糊子集，k为规则数。最后可求出模糊输出为:

式中W(2)k为第k条规则的适用度。

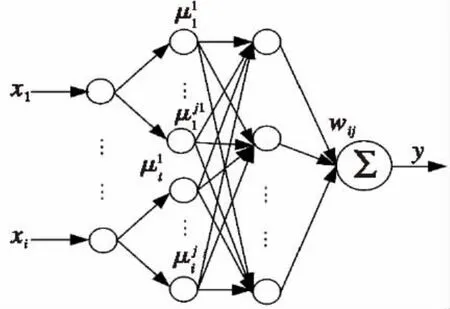
图2 模糊神经网络结构图Fig.2 The structure diagram of fuzzy neural network

(2)学习算法

模糊神经网络每一层的输入输出由fa和g(a)表示，隶属函数采用高斯函数:

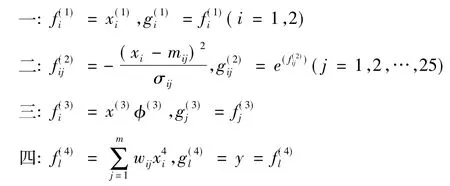
式中mij和σij为隶属函数的参数。

采用BP学习算法对隶属函数进行网络学习，设误差代价函数为式中T和y分别为模糊神经网络的期望输出和实际输出。根据梯度下降法可以得出:

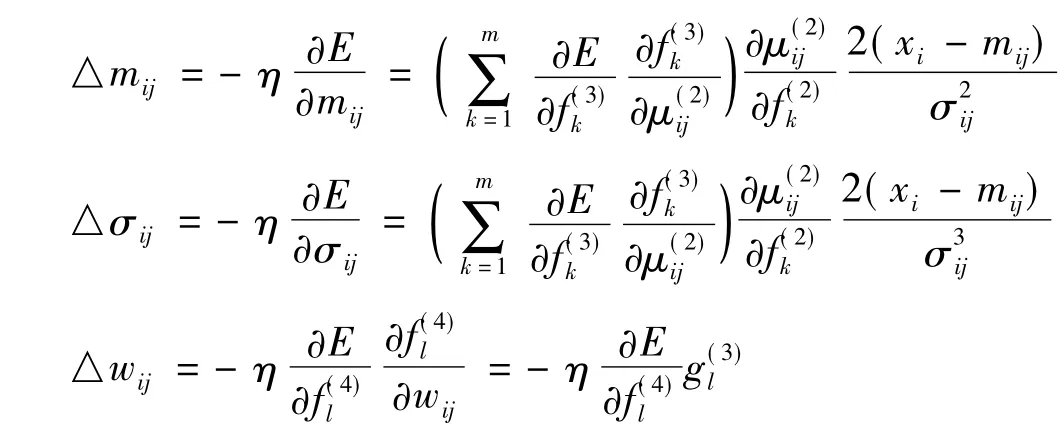
需要调节的学习算法为:

其中η为学习率，且0＜η＜1.t为离散时间变量。

同理可求得当γ和θ为系统输入时的控制器输出y1，则系统总控制律为:

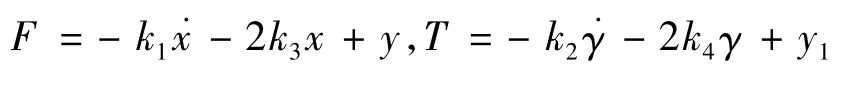
3 仿真分析

通过Matlab进行仿真。对于系统输入和输出三个变量分为5个模糊域，共25条规则［11］，训练样本采用一般模糊控制器，经学习训练的到训练精度小于0.001，取学习率η=0.5.系统参数如下:L=5 m，Dx=2.5 N·s-1/m，g=9.8 m/s2，M=100 kg，m=200 kg，J0=200 kg·m2，取，k1=339，k2=48，k3=140，k4=169，设x，γ的初始值为-20 m，0.5 rad.为了证明控制器的鲁棒性能，在30 s时加入幅值为0.5的阶跃干扰。仿真结果如图3-9所示。

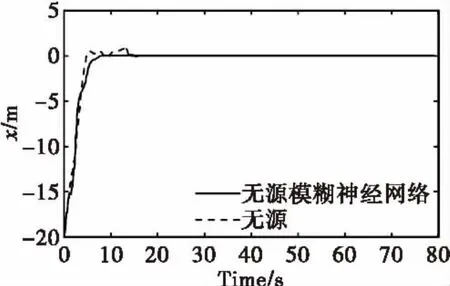
图3 小车位移变化曲线Fig.3 The changing curve of position trolley

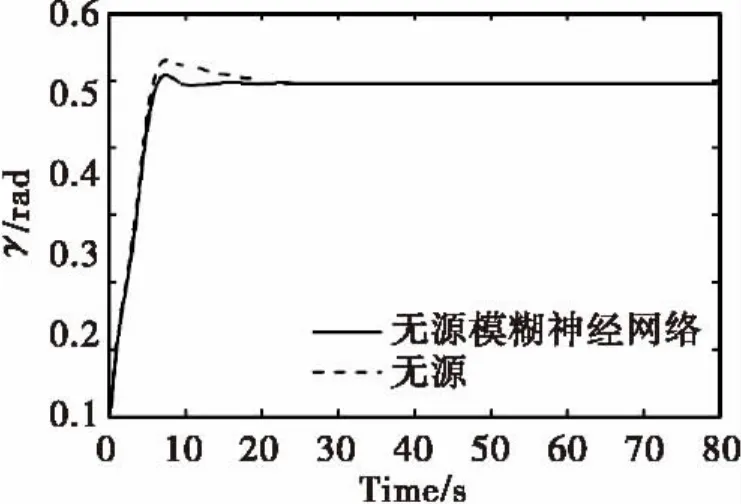
图4 γ变化曲线Fig.4 The changing curve of γ

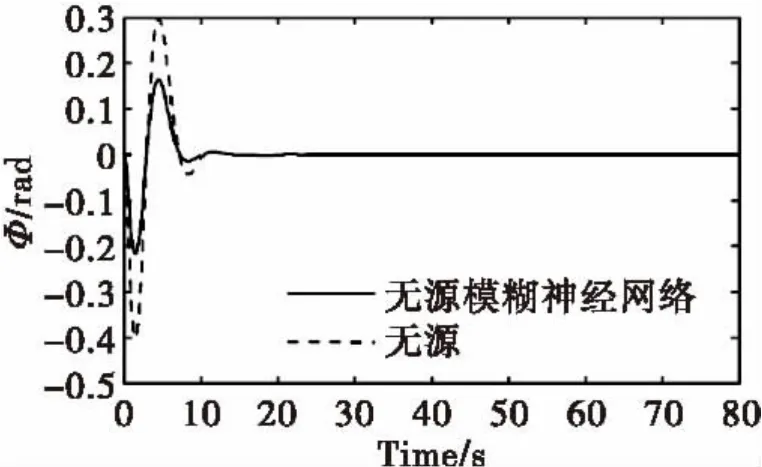
图5 摆角φ变化曲线Fig.5 The changing curve of φ

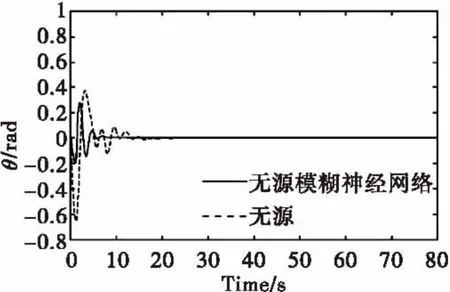
图6 摆角θ变化曲线Fig.6 The changing curve of θ

图7 加干扰时的小车位移变化曲线Fig.7 The changing curve of x with interference

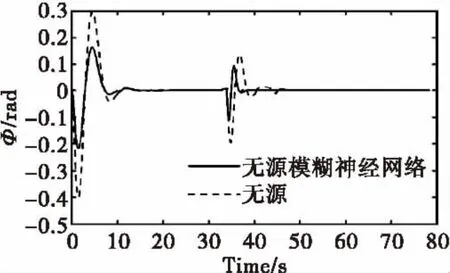
图8 加干扰时摆角φ变化曲线Fig.8 The changing curve of φ with interference

图9 加干扰时摆角θ变化曲线Fig.9 The changing curve of θ with interference

由图3-6可以看出，与一般的无源控制相比，本文提出的控制方法使得调节时间有所降低，摆动次数和角度有所减少，使得起重机更快更稳定地到达了指定位置。由此可见，无源模糊神经网络控制更具优越性。

图7-9为加干扰时位移x，摆角φ，θ的曲线变化，由图可知，在加入干扰后系统能在很短时间内稳定，说明了系统具有较强的鲁棒性。

4 结论

针对塔式起重机的小车定位和负载防摆进行了研究，提出了基于无源性的模糊神经网络控制方法。分析系统的无源性，在此基础上设计模糊控制器，并利用神经网络强大的自学习能力调节模糊规则中的隶属函数，克服了一般模糊控制器设计时模糊变量的隶属函数靠人工经验获取的不足，实现了塔机的准确定位与防摆，仿真结果表明了该方法的优越性和可行性。

［1］王广超，王少华.桥式起重机运行过程中的消摆控制［J］.起重运输机械，2012(9):27-30.

［2］栗三一，余发山，卜旭辉，等.桥式起重机位置跟踪及防摆的迭代学习控制［J］.电子测量与仪器学报，2014，28(2): 184-190.

［3］DOMINIK SCHINDELE，INGOLF MENN.Nonlinear Optimal Control of an Overhead Travelling Crane［C］∥International Conference on Control Applications，IEEE，2009:1045-1050.

［4］刘德君，纪宏利，白晶.基于非线性PID的吊车防摆与定位控制［J］.微计算机信息，2007，25(11):51-52.

［5］郭一卓，蔺素宏，蒋权.起重机减摆系统装置研究［J］.机械工程与自动化，2014，10(2):26-28.

［6］马海峰，丁国富，黄文培，等.起重机定位和防摆的变论域模糊控制［J］.系统仿真学报，2014，26(2):425-429.

［7］WANG ZHENYAN，CHEN ZHIMEI.On PSO Based Fuzzy Neural Network Sliding Mode Control for Overhead Crane［J］.Advances in Intelligent and Soft Computing，2011，12(5):563-572.

［8］高武龙，陈志梅，孟文俊.基于无源性分数阶控制在起重机防摆中应用［J］.太原科技大学学报，2014，35(2):132-136.

［9］孙辉，陈志梅，孟文俊.塔式起重机的神经网络滑模防摆控制［J］.系统工程理论与实践，2013，33(10):2708-2713.

［10］肖鹏，王冰.模糊神经网络技术在防摇控制系统中的研究与应用［J］.起重机运输，2013，(11):21-23.

［11］何航，宛西原，胡宇.起重机模糊神经网络防摇摆控制仿真研究［J］.自动化与仪器仪表，2014，171(1):10-14.

Anti-swing Control of Fuzzy Neural Network of Tower Crane Based on Passivity

WANG Yu-ting，CHEN Zhi-mei，SHAO Xue-juan

(School of Electronic Information Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China)

Aiming at anti swing of tower crane，a control method of fuzzy neural network based on passivity is proposed.The passivity of system is analyzed by establishing the Lyapunov energy function，and the membership function can be learned to rely on neural network by using fuzzy control on this basis.The accurate mathematical model of system was no more needed.In this method the position and anti swing of tower crane can be related.The robustness of system also be improved.The simulation results proved the feasibility and effectiveness of the method.

tower crane，passivity，fuzzy neural network controller，position，anti swing

TP273

A

10.3969/j.issn.1673-2057.2015.02.002

1673-2057(2015)02-0087-06

2014-10-27

山西省自然科学基金(2014011020-2，2014011020-1)

王雨婷(1989-)，女，硕士研究生，主要研究方向为先进控制理论及应用。