基于最优核时频分布的装甲车辆微多普勒特征分析*

张万君，牛敏杰，杨雨迎，吴晓颖

（装甲兵工程学院，北京 100072）

基于最优核时频分布的装甲车辆微多普勒特征分析*

张万君，牛敏杰，杨雨迎，吴晓颖

（装甲兵工程学院，北京 100072）

依据微多普勒效应原理，构建了装甲车辆微动的雷达回波数学模型，推导了装甲车辆点目标的回波信号解析关系，并针对回波信号非平稳非线性的特点，利用最优核时频分布结合求时频脊的方法，仿真提取了装甲车辆微动线目标的回波微多普勒特征。仿真结果表明：线目标模型更能凸现、解析装甲车辆微动特征；采用的最优核时频分布结合求时频脊方法，具有比经典二次型分布更好的时频像，能较好地提取出微多普勒特征。最后，利用该方法分析了低信噪比下目标加速度、身管长度等参数对微多普勒特征的影响。

装甲车辆，线目标，时频分析，微多普勒效应

0 引言

装甲车辆作为地面战场的主要武器装备，其体积、结构、材质相近，这给特征识别带来很大困难，微动概念的提出为刻画目标精细结构提供了新的思路。微动即目标或组成部件在雷达径向上相对质心的微小运动，装甲目标上的典型结构，如炮塔、身管、履带等的运动，都可以看作微动，微动在雷达波的照射下会产生多普勒频移，这种现象被美国海军研究室的V.C.chen发现并命名为微多普勒效应［1］。微多普勒主要应用在弹道导弹识别［2-3］、生命探测［4］等领域。Chen讨论了点目标典型微动（如振动、转动）的微多普勒的数学模型［5-6］，以后文献也多以点目标、传统时频算法为主分析微动特性。本文提出了利用微动线目标模型分析炮身运动，基于最优核时频分布结合求时频脊的方法分析装甲车辆典型微动产生的微多普勒特征，相比传统方法模型更准确、时频聚集性更好，能更有效地估计目标微动特征。

1 装甲目标微动雷达回波数学模型

炮塔作为坦克、步战车等装甲目标的典型特征，不尽相同，不同种类以及不同型号的装甲车辆具有其独特的电磁散射特征，利用微多普勒效应分析这些特征可以作为装甲目标识别的重要依据。如图1所示为雷达照射装甲车辆运动引起的微动回波模型示意图。

图1 装甲目标微动的雷达回波模型

以雷达位置Q作为坐标中心建立雷达坐标系（U，V，W），以身管在炮塔的端点位置O为中心建立参考坐标系（X，Y，Z），参考坐标系与雷达坐标系平行，可以随车体平动。假设坦克相对雷达的径向速度为v（远离雷达为正方向），目标方位角为α，俯仰角为β，雷达与目标初始径向距离为R0。

当P点为炮身上任一散射点时，P点到参考坐标系中心距离为OP=l，炮身的方位角为γ，俯仰角为δ，γ0和δ0为炮身初始相位，炮身转动和俯仰角速度分别为ωr和ωh（图1箭头所示为正方向），则t时刻O点到雷达的距离为Rt=R0+vt，炮身方位角为γt= γ0+ωrt，身管长度l=L，俯仰角为δt=δ0+ωht。那么，t时刻 O点在雷达坐标系中的坐标为（Rtcosβcosα，Rtcosβsinα，Rtsinβ），散射点P在参考坐标系中的坐标为（lcosγt，lsinγt，lsinδt）。设雷达发射单频连续信号：，其中f0为载频。根据图（1）所示的三角关系，t时刻散射点P到雷达的距离为：

则从散射点P返回的信号为：

其中ρ（x，y，z）表示P点的反射率，为了便于研究，将其设为ρ（x，y，z）=1，c为电磁波的传播速度，一般取c=3×108（m/s），φ（t）为瞬时相位，s（t）为复包络。当不计炮身俯仰运动，由式（1）、式（2）得到散射点P简化的复包络的相位为：

由复包络相位φ（t）产生的多普勒频率为：

显然，装甲车辆运动产生的多普勒频率分为两部分，即车体平动产生的多普勒频率fpd和炮身运动产生的微多普勒频率fmd。而且，从式（2）的点目标微动引起的雷达散射回波信号sp（t）来看，是一种非线性非平稳信号，传统意义上的线性傅里叶频谱分析不能有效地描述微动的频率特性，为此，采用时频联合分析方法（JTFA）来解析装甲车辆微动的时间-频率对应关系。

2 装甲车辆微动点目标雷达回波时频特性分析

通常，在描述非平稳信号的能量变化时，由于能量本身是一种二次型表示，二次型时频分布是一种更加直观和合理的信号表示方法［7］。下面通过仿真分析，寻求装甲车辆点目标微动信号的解析、处理方法。

仿真参数：设连续波信号载频f0=1 GHz、初始距离 R0=2 km、径向速度 v=15+0.2t、l=2 m、α0=π/4、β0=π/4、γ0=π/3、θ0=π/8、wr=π/3 rad/s、wh=π/10 rad/s，仿真时间15 s，加入信噪比SNR=1的高斯白噪声，仿真结果采用归一化频率表示。

2.1 最优核时频分布

最优核时频分布（optimal kernel time frequency representation）是一种二次型的时频算法，能自适应刻画信号细节，保证时频分辨率和聚集性的同时，有效抑制了交叉干扰项［8］。装甲车辆散射点目标回波信号sp（t）在区间［t-T，t+T］的AOK分布可以表示为：

式中：s（t）是信号sp（t）的解析表达，ω（u）是对称的窗函数，t是窗函数的中心。设|u|＞T（T为窗长），ω（u）=0，在任意时刻t，只有在［t-T，t+T］范围内才能计算它的模糊函数，从而自适应求出回波信号s（pt）的细节特征，得到相应自适应最优核函数φ（t；θ，）。取核函数沿任意径向剖面Gauss型的二维函数：

利用优化准则［6］：

求得最优核函数，使回波信号变换后的自有分量集中在原点周围而交叉项远离。根据核函数的低通滤波性，由式（8）的径向高斯核函数的最优核参数β（1≤β≤5），对交叉项得到较好抑制。仿真表明，回波信号的AOK分布利用优化准则取矩形窗长2T=200，选取参数β=2时成像较好。理论上Wigner-Ville分布具有最好的时频聚集性［9］，比较AOK分布和Wigner-Ville分布、平滑伪Wigner-Ville分布。如图2（a）是sp（t）的Wigner-Ville分布时频像，（b）是128点汉明窗的平滑伪Wigner-Ville分布，（c）是AOK分布，（d）是AOK时间-频率-幅值三维像。

图2 点目标微动回波AOK时频分布

图2 中横坐标为采样时间序列，采样间隔0.01 s，纵坐标为归一化频率，颜色深度表示幅值。仿真结果表明：尽管WVD对散射点目标P回波信号sp（t）有很好的时频聚集性，但产生了严重干扰项，很难分辨出真实信号；SPWVD分布对交叉项和噪声的抑制效果较好，身管在雷达视线投影较大时信号强度较强（如时间序列0～100），反映图中颜色较深，但身管在雷达视线投影较小时，图像产生了严重缺失（如时间序列100～200），即SPWVD的抑制能力以牺牲时频分辨率和聚集性为代价。可以看出AOK法在抑制交叉项和噪声的同时在整个时间序列都有较好聚集性。

2.2 时频脊

尽管通过AOK分布对于点目标微动回波信号能达到较为理想的时频像，但对于信噪比低的复杂目标信号，则信号聚集性较差。对于点散射回波sp（t）分辨率较好的时频像图2（a），可求解其时频像中瞬时频率的局部极值点，这些以时间为变量的极值点计算过程可以看作是时频脊线的提取［10］。图3中（a）为式（4）数值计算得到微动多普勒近似曲线，（b）为对信噪比SNR=1时点目标微动回波信号求时频脊。结果表明：微多普勒数值解和仿真时频脊线基本吻合，目标微动时频信号被有效地从杂波中提取出来，并且具有很高的时频聚集性，证明了该方法对提取点目标回波微多普勒特征的有效性和式（4）数值计算复包络简化是合理的。

图3 多普勒频率数值解和SNR=1时AOK分布时频脊

3 装甲车辆的微动线目标雷达回波分析

通过对炮身点目标微动回波信号sp（t）的分析，得出了利用AOK分布和求时频脊的方法能得到很好时频像。考虑整个炮身的回波散射，可以把炮身看作是N个离散散射点回波sp（t）在炮身轴线的积分，即n=0，l/N，2l/N，…，（N-1）l/N，l。得到炮身线目标调制回波的基带信号表达式sl（t）为：

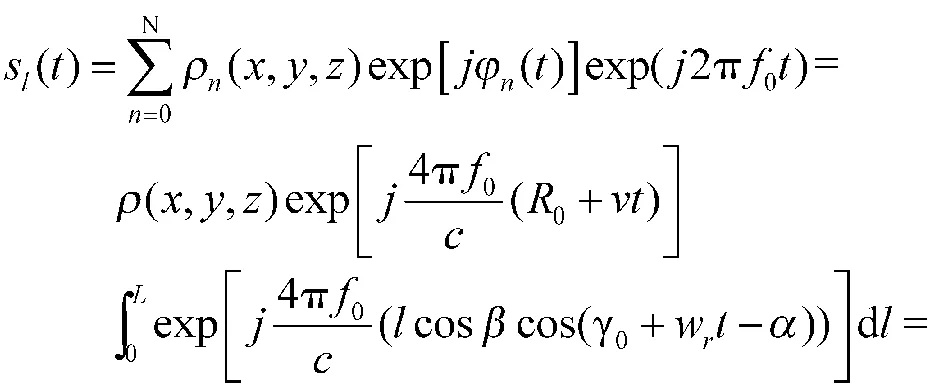
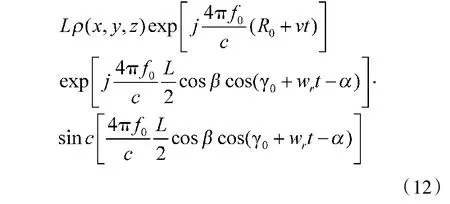
其中：

于是，炮身运动就可看作是由有限个离散点目标沿炮身轴线积分的线目标运动，通过改变仿真参数，利用自适应最优核时频理论和求时频脊的方法，可以分析装甲车辆不同微运动情况下的回波信号sl（t）的微多普勒时频特征变化。

3.1 改变身管长度

取不同身管长度，分析对目标微动回波信号sl（t）的影响。图4为取身管长度l1=2 m、l2=1 m时，仿真分析微动回波信号sl（t）的时频像。

图4 不同身管长度的微多普勒时频像

如图4所示，时频像中每隔300采样点出现峰值，即身管在雷达视线投影最大，在其他时间却很模糊，而时频脊的方法能清楚反应其峰值变化。时频脊中轴线为回波多普勒频率趋势，可看作平动产生的多普勒频率fpd，轴线周围规律变化的展宽是微多普勒频率fmd。仿真结果表明：当目标身管长度不同时，微多普勒时频像差异明显，时频脊的轴线趋势没有改变，和点目标微多普勒趋势基本一致。由时频脊反应的微多普勒带宽则随着身管长度的变化而改变，l1=2 m时，带宽峰值近似0.15，l2=1 m时，带宽峰值近似0.08，即目标身管长度等比例影响微多普勒带宽。

3.2 改变平动速度和加速度

取装甲车辆不同平动速度和加速度，分析对目标微动回波信号sl（t）的影响。图5为不同速度和加速度的时频像，（a）取v1=-17-0.2t，即改变目标的平动速度；（b）取v2=-15-0.15t，即改变目标平动加速度，对比分析目标在v=-15-0.2t时的时频像图4（a）。

图5 改变平移速度和加速度的微多普勒时频像

仿真结果表明：当改变目标的平动速度时，其微多普勒时频像在频率轴上发生了平移，平移量即是速度所对应的多普勒频率；当改变目标加速度时，时频脊趋势发生变化，随着加速度减小回波微多普勒在时频面上的“斜率”相应减小。目标平动速度和加速度使得微多普勒在时频面上产生频率轴平移和倾斜，不影响微多普勒的特征（如带宽、周期）。

4 结论

利用装甲车辆微动特征能有效分辨目标细节，本文从装甲车辆的微动对雷达回波微多普勒调制机理出发，利用线目标建立了装甲目标微动雷达回波微多普勒数学模型。和点目标模型相比，线目标模型能通过时频像展宽、周期等反应更多微动特征，对比传统的二次型分布，得出自适应最优核分布结合时频脊提取方法分析微动回波具有更好的时频分辨率和交叉项抑制能力。通过对低信噪比下微动线目标模型时频分析，得出了身管长度、车体平动速度、加速度、炮塔方位角速度对微多普勒的影响，为下一步利用微动识别装甲目标和微动参数估计提供了技术支撑。

［1］Chen V C.Micro-Doppler Effect in Radar Phenomenon，Model and Simulation Study［J］.IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）:2-21.

［2］皱小海，艾小锋.进动弹头双基地微多普勒特性分析［J］.电子与信息学报，2012，34（3）：609-615.

［3］Guo K Y，Sheng X Q，et al.Precise Recognition of Warhead and Decoy Based on Components of Micro-Doppler Frequency Curves［J］.Science China（Information Sciences），2012，55（4）:850-856.

［4］张翼，朱玉鹏.基于微多普勒特征的人体运动辨识［J］.西南大学学报，2010，32（3）：156-161.

［5］Chen V C.Doppler Signatures of Radar Backscattering from Objects with Micro-motions［J］.IET Signal Process，2008，2（3）:291-300.

［6］Chen V C，Ling H.Time-frequency Transforms for RadarImaging and Signal Analysis［J］.Artech House，2002（3）：11-15.

［7］张贤达.现代信号处理［M］.北京：清华大学出版社，2002.

［8］Sun B，Wang E，Ding Y.Time-Frequency Signal Processing for Gas-Liquid Two Phase Flow Through a Horizontal Venturi Based on Adaptive Optimal-Kernel Theory［J］.Chinese Journal of Chemical Engineering，2011，（2）：243-251.

［9］Cohen L.Generalized Phase-space Distribution Function［J］. Math Phys，1966（7）:781-806.

［10］Douglasl J，Richardgb.An Adaptive Optimal-kernel Timefrequency Representation［ J］.IEEETrans.on Signal Processing，1995，43（10）:2361-2371.

Analysis of Micro-Doppler Effect of Armored Vehicle Based on Adaptive Optimal Kernel Time-frequency Distribution

ZHANG Wan-jun，NIU Min-jie，YANG Yu-ying，WU Xiao-ying
（Academy of Armored Force Engineering，Beijing 100072，China）

An echo signal model of armored target is established by micro-motion line target model based on micro-doppler effect in this paper，for the non-stationary and nonlinear echo signal，feature parameters of echo signal can be extracted by adaptive optimal kernel time-frequency distribution（AOK TFR）and ridges-computed method.Simulation results show that the method is evidently better than point target model and other time-frequency methods，and the influences of different feature parameters such as the length of gun barrel and acceleration of vehicle on micro-doppler features at low signal-to-noise ratio is analyzed.

armor target，line target，time-frequency analysis，micro-doppler effect

TJ410

A

1002-0640（2015）06-0014-04

2014-04-26

2014-05-29

国家自然科学基金资助项目（61174219）

张万君（1965- ），男，吉林吉林人，博士，副教授。研究方向：武器系统综合运用。