叠层球面橡胶-金属弹性轴承等刚度设计研究
陈高升, 栗付平, 杨 岩
(1.北京航空材料研究院 减振降噪材料及应用技术航空科技重点实验室,北京 100095;2.总参陆航部军事代表局驻北京地区军事代表室,北京 100095)
叠层球面橡胶-金属弹性轴承等刚度设计研究
陈高升1, 栗付平1, 杨 岩2
(1.北京航空材料研究院 减振降噪材料及应用技术航空科技重点实验室,北京 100095;2.总参陆航部军事代表局驻北京地区军事代表室,北京 100095)
从理论上推导了叠层球面橡胶-金属弹性轴承各胶层的压缩刚度和扭转刚度计算公式,探讨了胶层压缩刚度、扭转刚度的等刚度设计方法,并将等压缩刚度和等扭转刚度设计方案的理论计算结果、有限元仿真结果分别与未进行等刚度设计方案的结果分别进行了计算和对比,结果表明,等刚度设计可以很大程度上消除不同胶层之间的刚度差异,各胶层压缩刚度和扭转刚度的理论计算结果与仿真结果基本吻合。
弹性轴承;等刚度设计;压缩刚度;扭转刚度;有限元仿真
叠层球面橡胶-金属弹性轴承是由具有相同球心的多层球形橡胶层及金属隔片相互交替粘接的复合结构,其作为直升机旋翼系统的重要构件,在桨毂和中央件之间起柔性连接作用,通常在一定的压力和扭转及弯曲载荷下使用,减小桨叶旋转过程中对中央件产生的扭转、挥舞、摆振载荷,弹性轴承的各向刚度性能指标对旋翼系统的动态特性有重要影响。因此,对弹性轴承进行设计时,其各向刚度的预先准确计算就十分重要。国外从上世纪60年代开始就对层状弹性轴承进行了大量研究,主要集中在弹性轴承的结构设计[1~3],弹性轴承动态特性分析[4],弹性轴承的材料及性能试验方法[5],弹性轴承在不同载荷条件下的力学特性[6,7]及寿命预测[8]等方面,并总结出了一套弹性轴承的设计方法及经验公式,在此期间形成了大量的相关专利[9,10]。国内对弹性轴承的研究则起步较晚,从上世纪80年代才开始研究,由于国外长期的技术封锁,有关弹性轴承的研究成果公开的文献很少,导致国内弹性轴承的研究水平与国外存在较大的差距,在弹性轴承理论方面的研究成果较少[11,12],没有形成系统成熟的理论,最近的研究也主要以弹性轴承的结构设计[13~15]及试验研究[16]为主。国外学者Donguy[1]对叠层球面弹性轴承刚度计算的研究较早,引入了形状因子,给出了压缩刚度和扭转刚度的近似计算方法,Lord公司的设计报告[2]中也给出了该结构弹性轴承压缩刚度和扭转刚度的类似计算公式,此外在文献[3,8]中对叠层球面弹性轴承压缩刚度和扭转刚度的计算方法均有介绍,但上述文献中给出的刚度计算公式均不完全相同。国内的颉连元等对叠层球面弹性轴承结构研究较早,在文献[13]中给出了弹性轴承的压缩刚度、扭转刚度和弯曲刚度的相关计算公式。以前对弹性轴承刚度计算方法的研究只简单地给出了其计算公式,没有通过具体算例与试验或有限元对比进行佐证,其各自的精确性及有效性还有待考证。本研究主要从理论上推导了层状球面弹性轴承的压缩刚度和扭转刚度计算公式,以该理论计算公式为基础,对弹性轴承的外部构型进行了合理简化,重点从理论上对球面层状弹性轴承在压缩和扭转载荷下的等刚度设计方法进行了探讨,以具体算例对等刚度设计和非等刚度设计两种结构进行了比较,并同有限元计算结果进行了对比分析。等刚度设计的目的是使各胶层在承载条件下的应变几乎相同,从而保证各胶层的寿命几乎相等,防止局部胶层应变过大提前出现疲劳破坏,从而大幅提高弹性轴承的疲劳寿命,该方法可为叠层球面橡胶-金属弹性轴承在不同承载条件下的结构设计提供指导与借鉴。
1 弹性轴承刚度计算理论
1.1 基本假设
为了从理论上计算层状球面弹性轴承的压缩刚度和扭转刚度,对弹性轴承作以下基本假设:(1)忽略金属件的变形,金属隔片和橡胶层在变形过程中始终保持球面形状不变;(2)胶层材料均匀,各向同性;(3)胶层与金属隔片粘接牢固,无滑移现象;(4)胶层受到扭转变形时,忽略厚度和承载面积变化;(5)胶层的压缩及剪切变形符合虎克定律。
典型的球形弹性轴承的截面示意图如图1所示。

图1 叠层球面橡胶-金属弹性轴承截面示意图Fig.1 Schematic illustration of the cross section for laminated spherical rubber-metal elastomeric bearing
1.2 压缩刚度理论
对于弹性不可压缩材料,其轴向压缩刚度为:
式中:EC表示材料的压缩模量,压缩模量EC与弹性模量E0有以下关系:
(1)
式中:SF为形状系数;k为碳黑修正系数。形状系数可通过以下公式计算得到[1,2]
(2)
式中:RSi为第i层橡胶层的平均球面半径,mm;tRi为第i层橡胶层的厚度,mm;δOi为第i层橡胶的平均球面半径外缘角度,°;δIi为第i层橡胶的平均球面半径内缘角度,°。各参数的表示如图2所示。
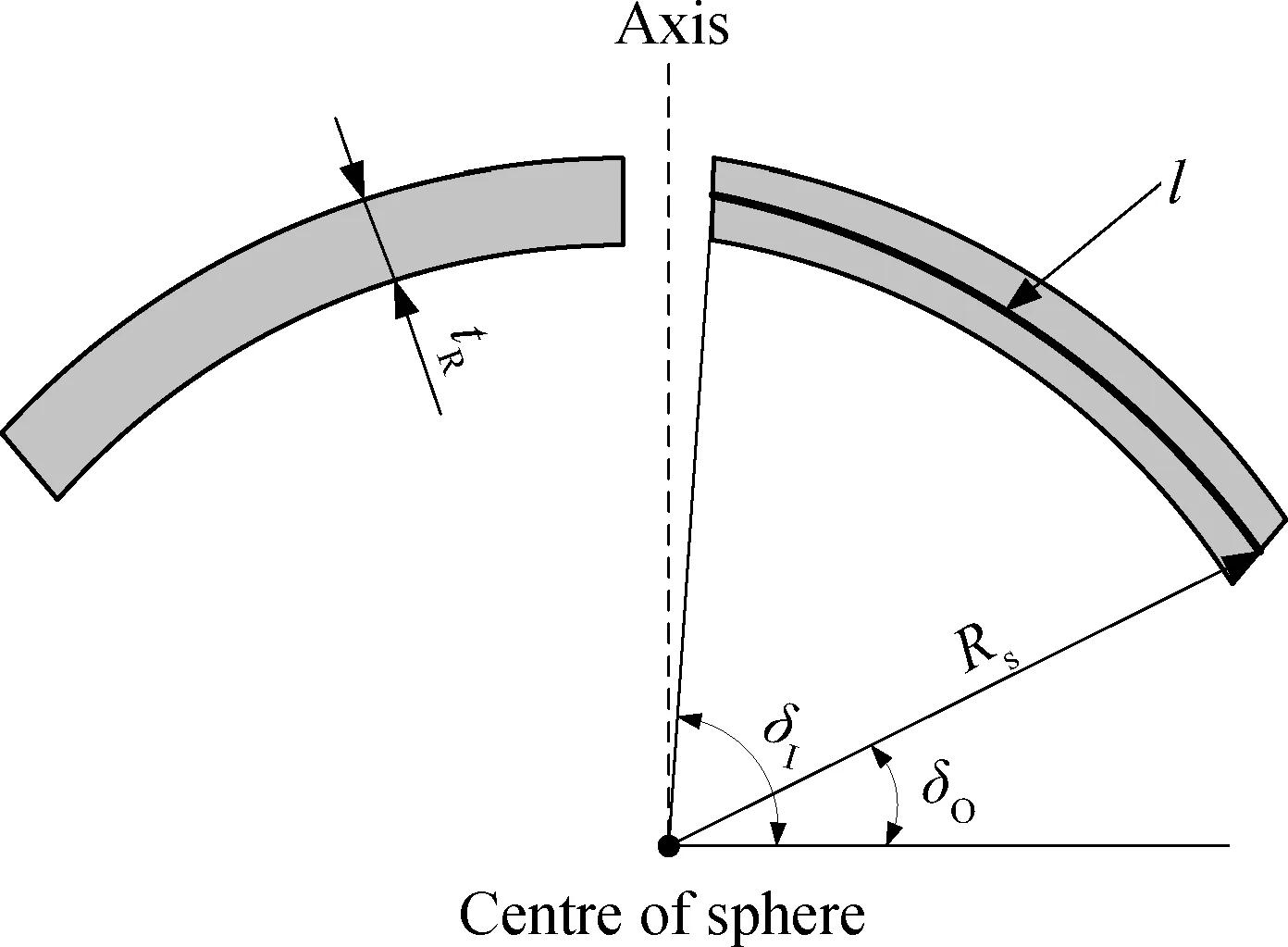
图2 胶层截面示意图Fig.2 Schematic illustration of the rubber layer
冠形球面胶层截面如图2所示,设其中截面曲线l(如图3所示)的方程为:
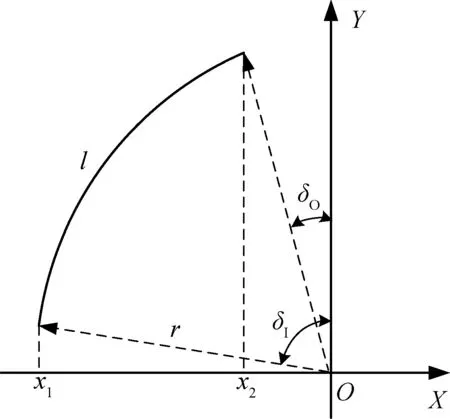
图3 胶层中截面曲线示意图Fig.3 Schematic illustration of mid-cross of the rubber layer section curve
x1=-rsinδI,x2=-rsinδo,其中r表示胶层中截面的球面半径。
该中截面的面积为:
=2πr2(sinδI-sinδ0)
则第i层橡胶的压缩刚度:
(3)
由于各橡胶层之间可以认为是串联关系,弹性轴承总的压缩刚度KC为:
(4)
1.3 扭转刚度理论
胶层的扭转刚度:
式中:KTi为第i层胶层的扭转刚度;G为橡胶材料的剪切模量;IPi为第i层胶层的惯性矩;为了得到第i层胶层的扭转刚度,先推导冠形球面胶层的惯性矩,如图4所示。设构成冠形球面胶层中截面的曲线l的方程为:

x1=rcosδI,x2=rcosδo。
冠形球面的惯性矩:
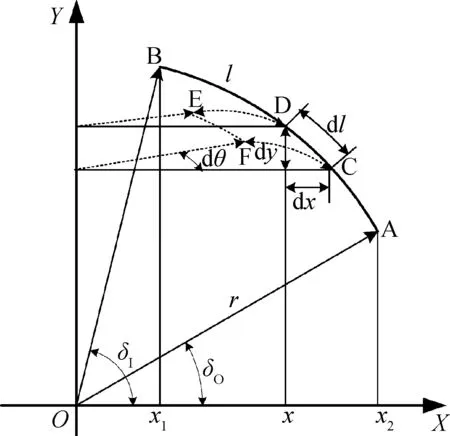
图4 冠形球面惯性矩计算示意图Fig.4 Schematic illustration of inertia moment calculation for sphere-shaped crown
令x1=rcos(δI)=rsin(α),则

(5)
故扭转刚度为:
(6)
考虑橡胶层形状系数的影响,第i层橡胶层的扭转刚度为:
(7)
由于各橡胶层之间可以认为是串联关系,弹性轴承总的扭转刚度KT为
(8)
2 等刚度设计
2.1 压缩刚度、扭转刚度等刚度设计方法
轴承各胶层的等刚度设计可以保证轴承在承受外载时各胶层产生较均匀的应变,使各胶层的应力分布更均匀,有效的减小胶层间的应力梯度,防止局部胶层提前破坏,提高轴承的整体疲劳寿命。胶层等刚度计算示意图如图5所示,这里对弹性轴承的外缘结构进行合理简化,假设弹性轴承各胶层在中截面的外缘近似处在同一直线上。
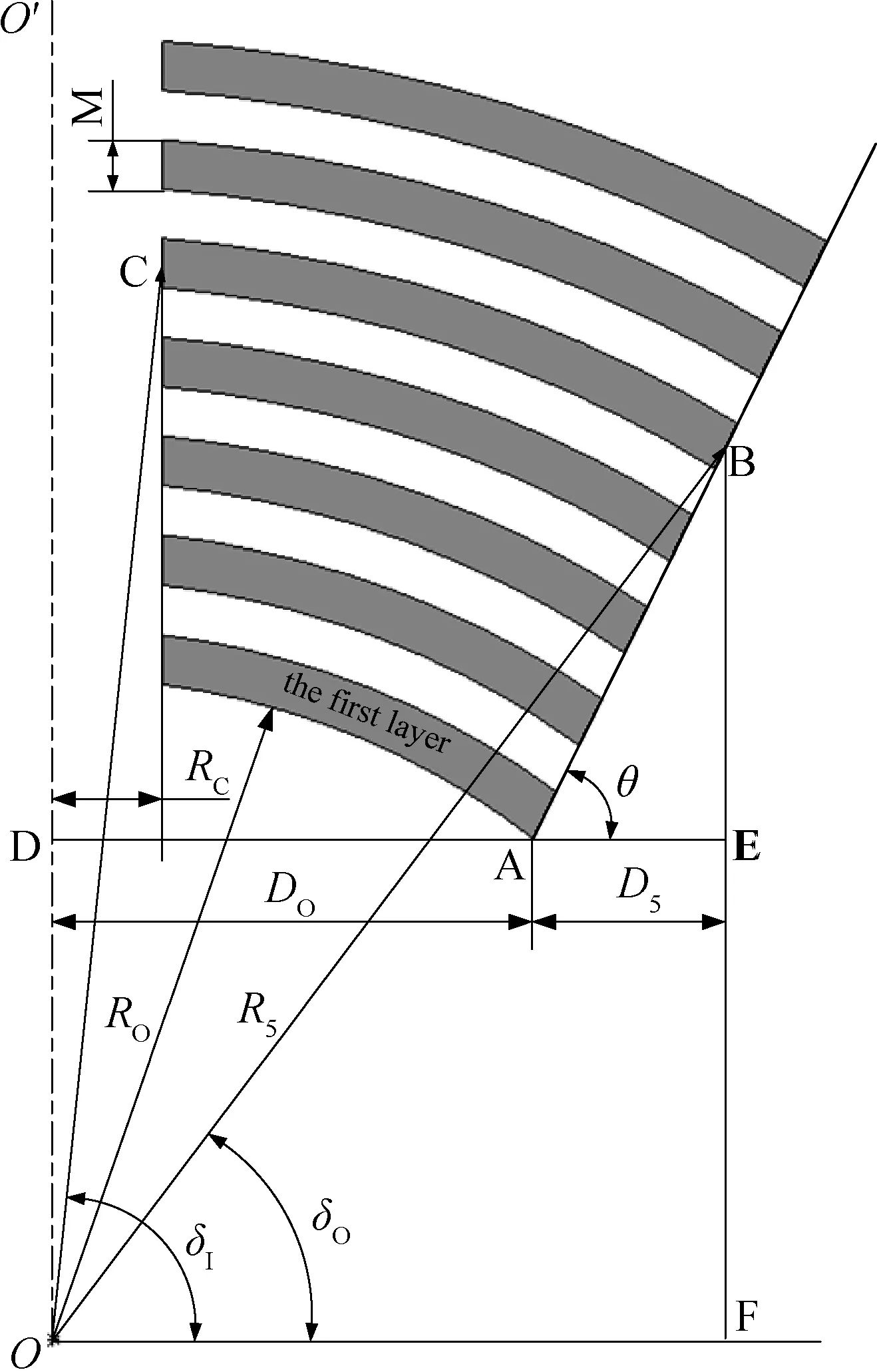
图5 球形弹性轴承各胶层等刚度设计示意图Fig.5 Schematic illustration of the equivalent rigidity design in every rubber layer of the spherical elastomeric bearing
已知条件:D0为第1层胶层与小接头接触表面的球冠半径,RC为注胶孔的半径,R0为第1层胶层与小接头接触表面的球半径,Mi为各金属隔片的厚度(假设相等且都为M),其中i=1,2,3,……,n-1,n为橡胶层的层数。θ为胶层外缘边线与水平面之间的夹角。
由图5可知:
Ri=R0+tR 1+tR 2+ …+tR i-1+
tR i/2 + (i-1)·M
等刚度设计满足的条件为:
(i=1,2,3,…,n)
(9)
等刚度设计时ai=1,(i=1,2,3,…,n)。若已知总的压缩刚度为K,橡胶层的层数为n,由式(4)可得:
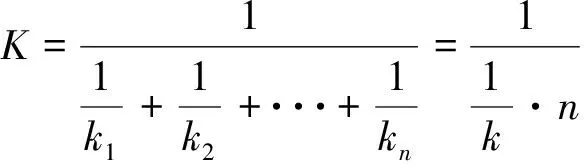
(10)
将前面的已知条件及k=nK代入方程(9)中展开可得到一个n维非线性方程组,求解该非线性方程组可以得到各橡胶层的精确厚度,从而完成总压缩刚度为K的轴承零件各胶层的等压缩刚度设计。求解非线性方程组可借助Matlab符号计算语言,通过优化算法编程实现。
当已知轴承总刚度的情况下,还可以完成特定橡胶层特定刚度的设计。由于在实际工作当中,弹性轴承最先疲劳破环的往往是靠近小接头的前两层胶层,因此可以使这两层胶层的刚度大于其他各层的刚度。如将第1和第2层胶层的刚度设计为ak(a>1),其他n-2层胶层的刚度设计为k,则对于该n层胶层的球形弹性轴承,总的压缩刚度为:

(11)
将k值代入(9)式求得各胶层的厚度,其中a1=a,a2=a,ai=1(i=3,4,…n),即可完成特定胶层特定刚度的设计。扭转刚度的等刚度设计方法与压缩刚度相似,不再详细论述。
2.2 压缩刚度、扭转刚度等刚度设计理论结果与仿真结果比较
为了验证前述等刚度设计理论的有效可靠性,现给出3种胶层厚度的分布方案,方案1为普通的胶层分布方案,方案2和方案3分别为等压缩刚度设计和等扭转刚度设计各胶层的厚度分布,各胶层厚度分布如图6所示。由图6可知,等压缩设计方案和等扭转设计方案胶层厚度的分布趋势均是由小接头向大接头逐渐增加,等扭转设计方案胶层厚度增加趋势更为明显。

图6 胶层厚度分布方案Fig.6 Thickness distribution plan of the rubber layer
为了便于比较,将方案1的压缩刚度和扭转刚度分别与方案2,3进行对比,图7是方案1和等压缩刚度设计方案2之间各胶层压缩刚度的比较,图8是方案1和等扭转刚度设计方案3之间各胶层扭转刚度的比较。各胶层压缩刚度的理论结果由式(3)得到,扭转刚度的理论结果由式(7)得到,压缩刚度和扭转刚度的仿真结果均采用有限元方法计算得到。
由图7可知,对于方案1,胶层厚度相同时,胶层压缩刚度几乎呈线性增加的趋势,在胶层厚度变化时会出现刚度的骤然变化,各胶层的最大压缩刚度与最小压缩刚度的比值为1.4,胶层间的压缩刚度梯度变化较大,而方案2各胶层压缩刚度的理论计算值相对于方案1波动很小,没有出现相邻胶层刚度突变的现象,各胶层的最大压缩刚度与最小压缩刚度的比值为1.06,胶层间的压缩刚度变化梯度明显减小。同时也可发现,方案2各胶层压缩刚度的仿真值随胶层序号的增加呈先增加后下降的趋势,除前3层胶层外各胶层的压缩刚度仿真结果不同程度大于理论计算结果,仿真结果与理论计算结果的最大误差为4.5%,采用两种方法计算得到的结果一致性较好,通过(4)式计算得到总的等效压缩刚度(分别为234kN/mm和237kN/mm)也基本一致。
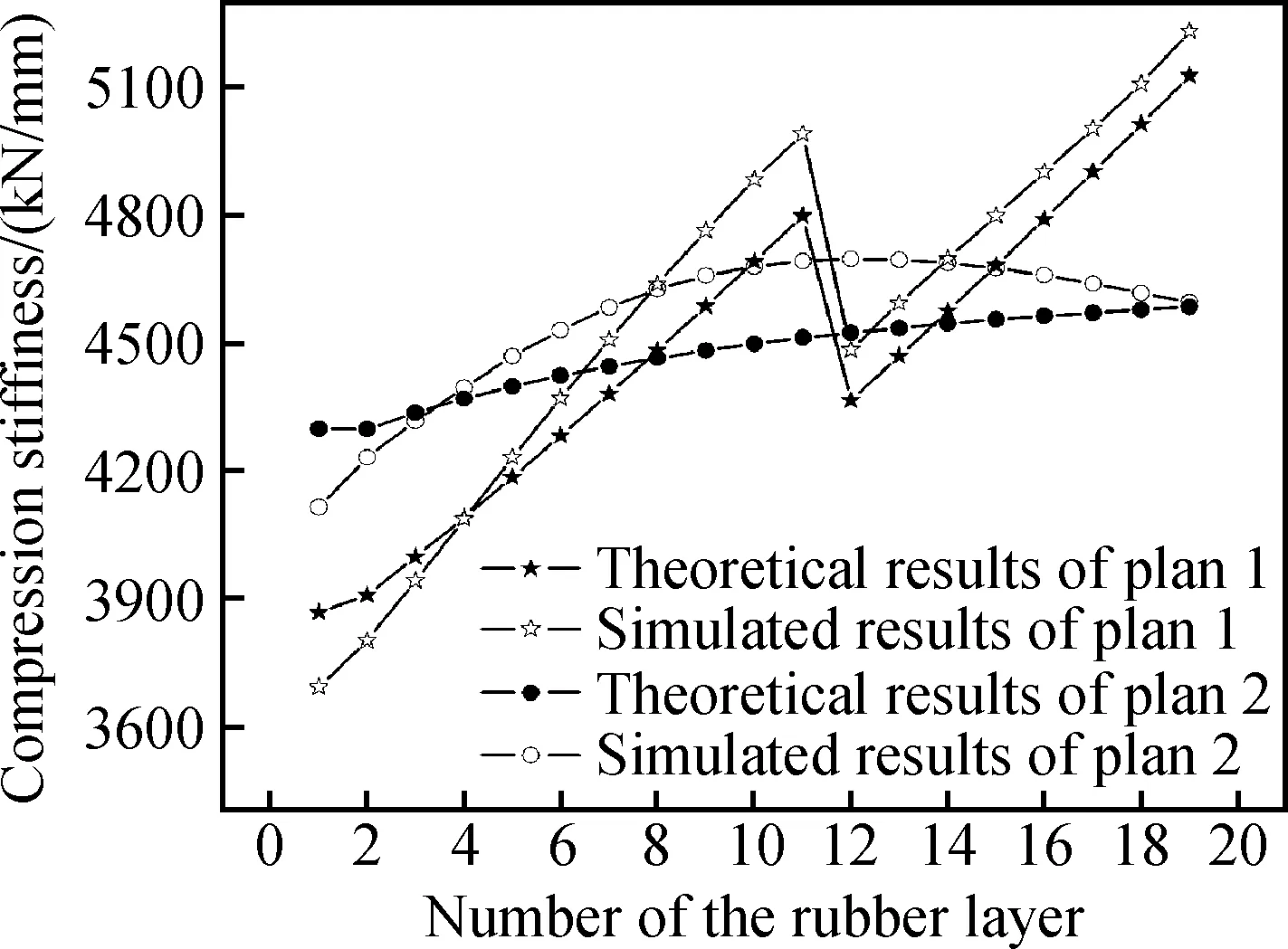
图7 方案1、方案2各胶层压缩刚度理论计算结果与仿真结果比较Fig.7 Comparison of theoretical results and simulated results of compress rigidity in every rubber layer of plan 1 and plan 2
由图8可看出,方案1胶层的最大扭转刚度为最小扭转刚度的2倍以上,在11层和12层厚度变化时扭转刚度出现骤降,方案3各胶层扭转刚度的理论计算值波动很小,没有出现相邻胶层刚度突变的现象,各胶层的最大扭转刚度约为最小扭转刚度的1.12倍,相对于方案1,胶层间的扭转刚度梯度值急剧减小,基本实现了各胶层的等扭转刚度设计。同时也可发现,各胶层扭转刚度的仿真结果与理论计算结果相差较大,前半部分胶层扭转刚度的仿真计算结果大于理论结果,后半部分各胶层扭转刚度的仿真计算结果小于理论结果,仿真结果与理论结果的最大误差出现在第1层,约为15%,通过(8)式计算得到总的等效扭转刚度分别为7.24N·m/°和7.43N·m/°,基本一致。

图8 方案1和方案3各胶层扭转刚度理论计算结果与仿真结果比较Fig.8 Comparison of theoretical results and simulated results of torsion rigidity in every rubber layer of plan 1 and plan 3
3 结论
从理论上推导了叠层球面橡胶-金属弹性轴承胶层压缩刚度(文中(3),(4)式)和扭转刚度(文中(7),(8)式)。
建立了叠层球面橡胶-金属弹性轴承压缩刚度和扭转刚度的等刚度计算模型,给出了具体的计算方法(文中(9),(10),(11)式),并通过具体算例对等刚度设计模型进行了验证,与非等刚度设计结果进行了对比分析,结果表明等刚度设计能够明显减小各胶层之间的刚度差异。
对叠层球面橡胶-金属弹性轴承压缩刚度、扭转刚度理论计算结果及仿真结果进行了对比研究,结果表明压缩刚度和扭转刚度的理论计算结果与仿真结果均基本吻合。各胶层压缩刚度仿真结果与理论结果的最大误差为4.5%;各胶层扭转刚度的理论计算结果与仿真结果存在的误差较大,约为15%,但总的等效扭转刚度基本一致。
[1] DONGUY P. Design and development of a helicopter rotor hub and elastomeric bearing[C]// Structure Dynamics and Materials Conference. New York: Technique Papers On Dynamics And Loads, 1970, 10-39.
[2] Lord Corporation. LASTOFLESRbearing design guide[R]. Aerospace Products Engineering Lord Corporation, PE76-006, 1976.
[3] STANTON J F,ROEDER C W, Elastomeric Bearing Designs, Construction and Materials[M]. Washington: Transportation Research Board, 1982.
[4] SHABANEH N, ZU J W. Nonlinear dynamic analysis of a rotor shaft system with viscoelastically supported bearings[J]. Journal of Vibration and Acoustics. 2002, 125(3): 290-298.
[5] TOPKAYA C, YURA J A. Test method for determining the shear modulus of elastomeric bearings[J]. Journal of Structural Engineering, 2002,128(6): 797-805.
[6] ABE M, YOSHIDA J,FUJINO Y. Multiaxial behaviors of laminated rubber bearings and their modeling(Ⅰ): experimental study [J]. Journal of Structural Engineering, 2004, 130(8): 1119-1132.
[7] RAVARI A K, OTHMAN I, IBRAHIM Z,etal. variations of horizontal stiffness of laminated rubberbearings using new boundary conditions[J]. Scientific Research and Essays, 2011, 6(14): 3065-3071.
[8] BAUMAN J T. Fatigue, Stress, and Strain of Rubber Components a Guide for Design Engineers [M]. Canada: Hanser Publications, 2008, 89-105.
[9] RYBICKI Robert C. Elastomeric bearing for a helicopter rotor:USA,US3782854[P]. 1974-01-01.
[10]MUYLAERT N W. Elastomeric Bearing: USA, US641304 8B1[P]. 2002-07-02.
[11]赵启元.层式橡胶弹性轴承[J], 材料工程, 1982(2): 39-43.
(ZHAO Q Y. Laminated Rubber Elastomer Bearing[J].Journal of Materials EngineerIng, 1982(2),39-43.)
[12]张劲,刘玉琦.橡胶球面弹性轴承的有限元分析[J], 航空学报, 1989,40(10): 122-126.
(ZHANG J, LIU Y Q. Finite element analysis for rubber elastomer bearing[J].ACTA Aeronautic Et Astronautica Sinica, 1989,10(4): 122-126.)
[13]颉连元.旋翼弹性轴承应用研究[J]. 直升机技术, 2002(3), 6-11.
(XIE L Y. Application research of rotor system spherical thrust bearing[J]. Helicopter Technique, 2002(3): 6-11.)
[14]陈高升,张连宏,栗付平,等.球面层状弹性轴承结构对其力学行为影响的有限元分析[J]. 材料工程, 2009(10), 15-19.
(CHEN G S, ZHANG L H, LI F P,etal. Finite element analysis for the influence of spherical layered elastomeric bearing structure on the mechanical behavior[J]. Journal of Materials Engineering, 2009(10), 15-19.
[15] 覃海鹰,刘晓宁,王丁伟,等.基于ANSYS的弹性轴承设计方法[J]. 直升机技术, 2009(4), 10-14.
(QIN H Y, LIU X N, WANG D W,etal. The Design method of spheric thrust bearing based on ansys[J]. Helicopter Technique, 2009(7),10-14.
[16]黄晓东,王卫卫,蒋伟光.直升机旋翼系统弹性轴承刚度特性试验方法研究[J]. 机械强度, 2012, 34(2), 270-273.
(HUANG X D,WANG W W, JIANG W G. Research of stiffness characteristics test method for helicopter rotor system spherical thrust bearing[J]. Journal of Mechanical Strength, 2012, 34(2),270-273.
Equivalent Rigidity Design Research of LaminatedSpherical Rubber-metal Elastomeric Bearing
CHEN Gao-sheng1, LI Fu-ping1, YANG Yan2
(1.Beijing Institute of Aeronautical Materials, Aviation Key Laboratory of Science and Technology on Materials and Application Research for Vibration and Noise Reduction, Beijing 100095, China; 2.Military Respective office of Aviation Department of the General staff Micitary Respeetive Bureau in Beijing,Beijing 100095, China)
The formulations of compression rigidity and torsion rigidity of laminated spherical rubber-metal elastomeric bearing were deduced by theoretical means, the designed means of equivalent compression rigidity and equivalent torsion rigidity were studied, for the equivalent rigidity plan and unequal rigidity plan, the theoretical results and finite element simulated results of compression rigidity and torsion rigidity are calculated and taken comparied respectively , the results show that the equivalent rigidity design can eliminate the rigidity difference between different rubber layer to a large extent, the theoretical calculated results of compression rigidity and torsion rigidity are basically identical with the simulated results in every rubber layer.
elastomeric bearing;equivalent rigidity design;compression rigidity;torsion Rigidity;finite element simulation
2015-01-22;
2015-03-15
国防基础科研计划资助(A052013002),
陈高升(1981—),男,硕士,工程师,主要从事橡胶减振器结构设计、结构强度与动力学分析研究,(E-mail)chen_max@163.com。
10.11868/j.issn.1005-5053.2015.3.013
V214.1; V257; V229+.7
A
1005-5053(2015)03-0077-06

