一种干扰受限场景下的双向中继选择方法

张庭园，李小兵，郑 宇，李 靖

(1.中国科学院微电子所，北京 100029；2. 中兴通讯股份有限公司，北京 100083；3. 西安电子科技大学 通信工程学院，陕西 西安 710071)

一种干扰受限场景下的双向中继选择方法

张庭园1，李小兵2，郑 宇3，李 靖3

(1.中国科学院微电子所，北京 100029；2. 中兴通讯股份有限公司，北京 100083；3. 西安电子科技大学 通信工程学院，陕西 西安 710071)

针对非对称双向中继通信系统，提出了一种干扰受限场景下的机会中继选择方法。该方法仅利用了中继节点的本地信道状态信息且实现复杂度低，适用于两个源节点的发射功率和阈值速率均不同的双向中继通信系统。仿真结果表明，在中高信噪比条件下，所提方法的性能接近于最优中继选择方法，且大大优于未考虑干扰的传统中继选择方法。

干扰受限；双向通信；中继选择

协作分集技术是无线网络中的一种新型分集技术，该技术通过在网络中的多个单天线终端之间进行协作来实现通信，此时可构成一种虚拟的多天线阵列，从而获得显著的分集增益。协作分集的实现方法是使用中继节点为源节点和目的节点之间的通信提供额外的传输路径，从而达到增强网络覆盖能力和提高网络传输量的目的。通过使用具有最佳瞬时信道质量的单个中继进行协作分集，机会中继可以获得与更为复杂的空时编码协作通信相同的分集增益。

由于放大转发(AF)双向中继协作通信系统可以在两个时隙中完成源节点之间的信息交换，具有较高的有效性及可靠性，近年来获得了研究者的广泛关注[1-3]。文献[4]针对AF双向中继系统，研究了系统业务的不对称性对中断性能的影响，并提出一种不对称AF双向中继选择方法。文献[5]详细介绍了双向中继系统的容量上限。针对两个源节点以及中继节点的功率都相等的情况，文献[6]提出了一种低复杂度双向中继选择方法。文献[7]提出了一种适用于双向中继传输的集中式中继选择方法，该方法需要持续估算整个系统中所有链路的信道状态信息，实现复杂度较高。

上述研究工作都是在忽略干扰的情况下进行的，而在实际的通信系统中，干扰总是存在的，尤其是相邻小区间的干扰总是不可避免的。文献[8]针对干扰受限场景下的单向中继系统，提出了几种简化的低复杂度中继选择算法。然而，双向中继系统在干扰受限场景下的中继选择问题，现有文献还较少涉及。为此，本文提出了一种干扰受限场景下的双向中继选择方法。需要特别指出的是，由于该方法还考虑了两个源节点的发射功率和期望的阈值速率均不同的情况，对存在干扰的实际基站-用户通信模型具有重要的参考价值。研究表明，所提方法以一种较低的系统复杂度，在高信干噪比时，达到了最优的中继选择系统性能。与最优的中继选择方法相比，该方法采用分布式的中继选择方法，通过比较两个源节点以及干扰源节点的信噪比来选择最优的中继节点，免去了持续估算整个通信系统所有链路的信道状态信息的过程，大大降低了系统复杂度。与传统的忽略干扰的中继选择算法[9]相比，该方法大大降低了系统的中断概率。

1 系统模型

假设存在一个简单的蜂窝系统网络，它是由两个相邻的小区组成，分别是(C，C′)，如图1所示。

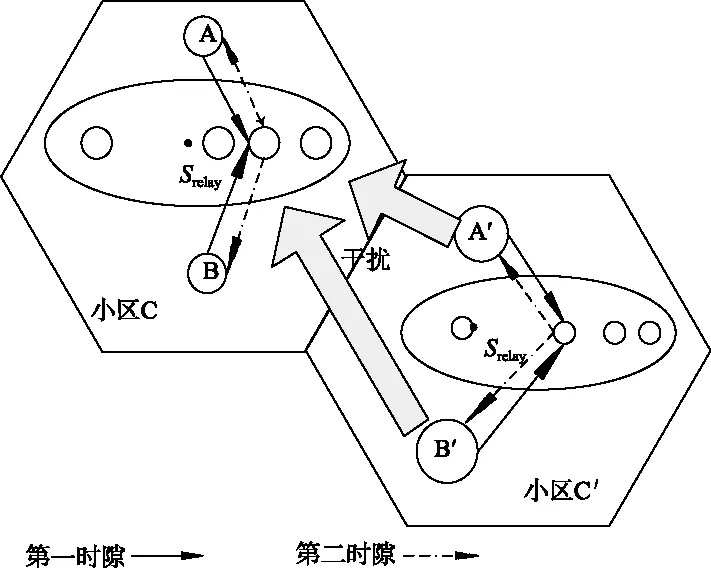
图 1 系统模型图

每个小区均由两个源节点A和B以及一簇中继节点Srelay={1,2,…,N}组成。假设所有节点均安装为单天线，其工作状态为半双工的，并且两个源节点A和B之间因为有深衰落而不存在直传路径，只能通过中继节点进行间接通信。

本通信系统分2个时隙完成整个传输过程，在第1个时隙中，两个源节点同时发射信号给中继节点，在第2个时隙中，被选择的中继节点k将接收到的叠加信号以及干扰和噪声放大后转发给两个源节点。这里认为干扰信号只对源节点到中继节点这一段有影响，对于目的端可以忽略。在此模型中，干扰信号被认为是从邻居小区C′的信号源A′和B′直接传到小区C中的中继R处的。假设源节点A和B的发射功率分别为Pa和Pb，干扰源节点A′和B′的发射功率为Pa′和Pb′，所有中继节点的功率均相等，且为Pr。

根据上述通信模型，中继节点k接收到的信号为

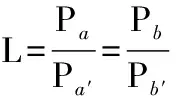
中继节点将接收到的信号Yk放大G倍后进行转发。G的计算公式为

(2)

式中：

(3)

(4)

则源节点A和B分别接收到的转发信号为

Yak=hakGYk+n2

(5)

Ybk=hbkGYk+n3

(6)

式中：n2和n3均为服从均值为0、方差为N0的复高斯分布的高斯白噪声。因为源节点A和B分别知道本节点所发送的信号，故可以进行自干扰消除。将G带入式(5)和(6)后，源节点A和B分别消除自干扰，然后得到源节点A和B接收到信息的信干噪比分别为

(7)

(8)

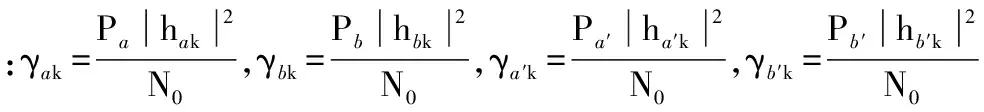
(9)

(10)

2 渐近的中继选择算法

假设该双向中继传输系统中两条互为反向的链路的传输速率阈值分别为τa和τb，则整个系统的中断概率可定义为两条链路中任意一条链路发生中断的概率。即

(11)

式中：γab=22τa-1，γba=22τb-1分别为满足传输速率门限的所需的最低的信干噪比，由式(11)可得最优的中继选择算法公式为

(12)

在中高信噪比条件下，式(7)和(8)中的二次项决定了该式的取值。此时式(7)和(8)可以分别简化为

(13)

(14)

将式(13)和(14)带入式(11)，可提出如下的机会中继选择方法

(15)

利用该方法，即可从N个可用中继中选出最佳中继来完成双向通信。需要指出的是，该渐近的机会中继选择方法可采用分布式时钟方式实现，无需知道整个系统的信道状态信息(CSI)，中继节点只需要根据第1个时隙中继节点接收到的源节点A和B以及干扰信号的源节点A′和B′发射信号的统计信噪比，即可确定最优的中继节点。因为不需要估算出具体的CSI，故该算法与最优的中继选择算法相比大大降低了系统的复杂度。

另外，该算法基于传统中继算法[2]，并不需要对传统算法做出很大的改动。由于干扰项并没有包含在算法中求最小值的运算里，故而该算法中的反馈信息与干扰信号无关，也就是与不考虑干扰信号存在的系统相同。所以已经成熟运用传统中继选择算法的系统可以很方便地更新到基于传统算法的渐近的中继选择算法，并不需要对求最小值部分做任何修改。

3 仿真结果和性能分析

图2所示为da=0.5时，中断概率随着SNR增加的变化曲线图。由此图可以看出，本文提出方法的性能曲线和最优方法的性能曲线随着信噪比的增加趋于重合，这说明采用渐近中继选择方法的双向通信系统在高信噪比情况下，系统性能与最优中继选择方法相同，且大大优于未考虑干扰的传统双向中继选择方法。图3所示为SNR=29dB，中断概率随着da增加的变化曲线。由此图可以看出，在高信噪比条件下，当中继节点在源节点之间改变位置时，本文提出的渐近中继选择方法的性能曲线和最优方法完全重合，且均优于未考虑干扰的传统选择方法。

图2 da=0.5时，系统中断概率随着SNR增加的变化曲线图

图3 SNR=29 dB，系统中断概率随着da增加的变化曲线

4 总结

本文针对存在干扰的非对称双向中继传输系统，提出了一种渐近的机会中继选择方法。研究表明，在中高信噪比条件下，与传统的中继选择方法相比，所提方法大大降低了系统的中断概率。与最优的中继选择方法相比，该方法在性能基本吻合的情况下，大大降低了系统的复杂度。

[1]RAYMOND H Y L, LI Y H, BRANKA V. Practical physical layer network coding for two-way relay channels: performance analysis and comparison[J]. IEEE Trans. Wireless Communications，2010, 9(2): 764-777.

[2]SHI J, GE J，LI J. Low-complexity distributed relay selection for two-way AF relaying networks[J]. IET Electronics Letters，2012, 48(3): 186-187.

[3]ZHENG J, BAI B, LI Y. Outage-optimal opportunistic relaying for two-way amplify and forward relay channel [J]. IET Electronics Letters，2010, 46(8):595-597.

[4]JI X D, ZHENG B Y, CAI Y M. On the study of half-duplex asymmetric two-way relay transmission using an Amplify-and-Forward relay[J]. IEEE Trans. Vehicular Technology，2012, 61(4): 1649-1664.

[5]WOOSEOK N, SAE Y C, LI Y H. Capacity bounds for two-way relay channels[M]. IEEE International Zurich Seminar on Communications，2008: 144-147.

[6]PRABHAT K U，SHANKAR P. Performance of two-way opportunistic relaying with analog network coding over Nakagami-m fading[J]. IEEE Trans. Vehicular Technology，2011, 60(4):1965-1971.

[7]SONG L Y. Relay selection for two-way relaying with amplify-and-forward protocols[J]. IEEE Trans. Veh. Technol，2011, 60(4): 1954-1959.

[8]IOANNIS K, JOHN S T, STEVE M，et al. Max-Min relay selection for legacy amplify-and-Forward systems with interference[J]. IEEE Trans. Wireless Communications，2009, 8(6): 3016-3027.

[9]ZHANG C S, GE J H，LI J，et al. Traffic-knowledge-based relay selection for asymmetric two-way AF relaying networks[J]. Science China Information Sciences，2013, 56(4):1-6.

责任编辑：薛 京

Relay Selection for Interference-limited Two-way Relaying System

ZHANG Tingyuan1，LI Xiaobing2，ZHENG Yu3，LI Jing3

(1.InstituteofMicroelectronicsofChineseAcademyofSciences,Beijing100029,China; 2.ZTECorporation,Beijing100083,China; 3.XidianUniversity,Xi’an710071,China)

In this paper, an opportunistic relay selection scheme for interference-limited two-way relaying system is proposed, which only requires the local channel state information at the relay nodes and has low implementation complexity. This scheme can be applied to the situation that two source nodes have different transmit powers and the expected transmission rate thresholds for them are unequal. Simulation results show that for the medium-to-high signal-to-noise ratios (SNRs), the proposed scheme performs closely to the optimal relay selection scheme and greatly outperforms the traditional interference-free relay selection scheme.

interference-limited; two-way communication；relay selection

国家自然科学基金项目(61101144)；国家科技重大专项(2013ZX03003001)

TN925

A

10.16280/j.videoe.2015.05.027

2014-07-29

【本文献信息】张庭园，李小兵，郑宇，等.一种干扰受限场景下的双向中继选择方法[J].电视技术,2015，39(5).