采用中国市场数据估计贝塔系数（β）过程中的注意事项及参数分析

一、贝塔系数的内涵及估计过程

（一）贝塔系数的内涵

贝塔系数（Beta coefficient）是一种风险指数，用来衡量个别股票相对于整个股市的价格波动情况。贝塔系数起源于资本资产定价模型（CAPM），它的真实含义是特定资产（或资产组合）的系统风险度量，是诺贝尔经济学奖得主美国著名经济学家威廉·夏普（William F.Sharpe）等人的研究成果，计算贝塔系数的公式为：

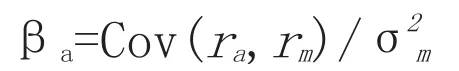
其中，βa是证券a的贝塔系数，ra为证券a的收益率，rm为市场收益率，Cov（ra，rm）是证券a的收益与市场收益的协方差，σ2m是市场收益的方差。

（二）贝塔系数的估计过程

估计目标公司的贝塔系数，首先要选择适合的可比公司，其次选择适合的参数口径计算可比公司的贝塔系数，比如选择市场指数、选择历史数据区间、选择收益周期等，最后再将可比公司的贝塔系数修正并调整为目标公司的贝塔系数，以下就从这几个方面分别进行分析。

二、贝塔系数估计过程中可比公司选择的注意事项

按照Damodaran的研究成果，影响一个公司贝塔系数的关键变量有三个：公司所处的行业和业务类型、经营杠杆、财务杠杆。经营杠杆和财务杠杆可以通过模型进行量化调整，行业和业务类型则需要通过选择可比公司确定，因此可比公司选择的合理性是贝塔系数估计值可靠性的基础，通过实例分析我们发现在选取可比公司时，需注意以下事项：

1.在公司只有单一业务的情况下，通过选择同行业具有相同业务类型的公司作为可比公司。对多种业务组合的公司，一是选择类似的多业务上市公司作为可比公司，二是将不同类型的业务分开，按其不同业务的权重对可比公司的数据进行加权处理。

2.在选择可比公司时，为达到合理反映个股系统风险的目的，应尽量避免选取有对贝塔值影响较大的特殊情况的可比公司，比如ST股、数据区间内有重大重组行为、有异常波动行情、无交易日较多（10周以上）的情况等。如果必须选择有特殊情况的可比公司时，则需要通过下文中参数口径选择以规避数据自身缺陷。

三、贝塔系数估计过程中参数口径选择分析及注意事项

贝塔系数估计通常涉及到市场指数选择、历史数据区间选择、收益周期选择。

（一）市场指数选择分析及注意事项

1.选择不同市场指数估计贝塔系数

我们选取了中国股票市场不同行业的100支样本股，控制数据区间为5年，收益周期为周收益率，选择市场常用的20个市场指数估计贝塔系数并进行观察，通过观察和分析我们发现：上证综合指数包含了所有上证交易所挂牌上市的股票且包含了所有大盘股，所以个股相对上证综合指数波动最大，得出的贝塔系数最大。市场指数中样本股规模越小，个股相对该市场指数的波动越小，所估计的贝塔系数则越小。从观察样本中发现贝塔系数估计值最低时对应的指数为创业板指数。

2.市场指数选择建议

研究表明估计贝塔系数选择市场指数的标准为：市场覆盖面广，加权指数，能较好反映市场波动情况，市场的贝塔系数理论上为1。基于这些原则及中国市场指数样本观察分析结果，我们认为沪深300指数能较好满足这些标准，其样本空间覆盖沪深两市，该指数是加权计算指数，能较好反映市场波动情况，且不同行业贝塔系数的估计值平均水平近似等于1。

（二）历史数据区间选择分析及注意事项

1.选择不同历史数据区间估计贝塔系数

选取以上同样100支样本股，市场指数选取沪深300指数，收益周期口径选取周收益率，对数据区间为1～10年（2005年～2014年）的贝塔系数估计值进行观察，通过观察和分析我们发现：

（1）数据区间为1年的样本股的贝塔系数估计值波动性差异明显，主要原因是样本点较少，偶然事件对个股贝塔系数估计值影响较大。

（2）随着数据区间的变长，贝塔系数估计值呈现出集中的趋势，数值趋同于1，该趋势在数据区间为6年时特征显著，见图1：

图1：不同时间区间计算的贝塔系数

（3）从样本股统计数据结果发现，采用的数据区间越长，贝塔系数的方差越能得到改善，其稳定性越高。

2.数据区间选择建议

（1）中国股票市场是一个新兴市场，市场的非系统风险干扰较多，需选择较长的数据区间弥补数据本身的缺陷；

（2）数据分析显示，数据区间大于6年时趋同性明显，导致贝塔系数时滞性明显，数据区间选择不宜超过6年。

笔者认为，采用中国市场数据计算贝塔系数时，宜采用5年的数据。Alexander和Chervany采用贝塔估计值的平均绝对离差来检验贝塔系数的稳定性，他们认为最佳估计周期是4—6年，国内大多数证券服务机构估计贝塔系数目前多采用时间区间为5年的数据。

（三）收益周期选择分析及注意事项

1.选择不同收益周期估计贝塔系数

选取以上同样100支样本股，市场指数选取沪深300，数据区间选取5年，对收益周期口径为日收益率、周收益率、月收益率的贝塔系数估计值进行观察，通过观察和分析发现：日收益率计算的贝塔系数估计值最为集中，月收益率计算的贝塔系数估计值比较分散。这种现象的主要影响因素是无交易日情况、可选取样本点数量、中国股票市场的涨跌幅限制等。国外研究表明，当采用不同的收益周期口径数据时，所得到的贝塔系数估计值有所差异，并将这一现象称为“时限效应”。“时限效应”的规律因贝塔系数的数值高低而有所不同，具体体现为：

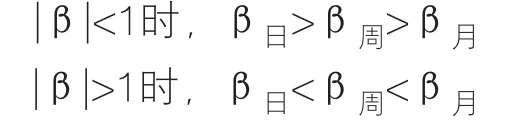
使用日收益率会提高回归中数据的可选样本观察量，但也会面临一个问题，即对于没有成交或者停牌导致较多无交易日情况，该期间的收益率为零，由此引起的偏差会降低个股收益与市场收益的相关性，也会钝化股票的贝塔系数敏感度。而以周或月作为收益周期，则能够显著减少这种非系统因素所带来的贝塔系数估计误差。

2.收益周期选择建议

（1）基于以上针对日收益率所提及的问题，按日收益率估计的贝塔系数估算往往会有明显误差，即流动性不足的公司会得到低于实际的贝塔系数，而流动性充足的公司会得到高于实际的贝塔系数。为了降低这些不可避免的特殊因素对数据产生的影响，一种是学习Michael（1908）的做法，即：剔出超过连续20天未发生交易的公司；另一种是选用周、月收益率计算贝塔系数以平滑数据本身的缺陷。

（2）基于样本数量选择的要求以及中国股市波动相对较大的特点，建议在时间区间选取5年的前提下，收益周期口径选择周收益率，以平滑非系统因素对贝塔系数的影响。

四、对贝塔系数进行修正和调整

（一）贝塔系数修正

对贝塔系数估计值进行趋同调整是基于一项研究的结论，即随着时间的推移，所有公司的贝塔系数都有趋于某一固定值的趋势。在市场上生存下来的企业往往随着时间的推移扩大企业规模，业务变得更加多样化，有更多的资产到位，产生更多的现金流，所有这些因素都会导致贝塔系数趋同。

一般来说，大多数机构采用一种简单的方法来调整其回归得到的贝塔系数，使其趋于一致。例如，Bloomberg是这样调整回归得到的贝塔系数的：

调整后的贝塔系数=回归得到的贝塔系数×0.67+1×0.33

（二）贝塔系数调整

经营杠杆、财务杠杆是贝塔系数的关键驱动因素，需要将可比公司回归计算得到的贝塔系数根据目标公司的经营杠杆、财务杠杆进行调整。调整过程是：首先将可比公司的平均有杠杆的贝塔系数按照公式转化为无杠杆的贝塔系数，再将该贝塔系数按照目标的公司的经营杠杆和财务杠杆转化为目标公司的有杠杆贝塔系数。

（1）对经营杠杆进行调整

经营杠杆是公司成本结构的一个函数，通常定义为固定成本和总成本之间的关系。具有较高的经营杠杆的公司（相对总成本有较高的固定成本）息税前利润的波动性相对于生产类似产品的低经营杠杆公司要大。其他条件相同时，经营杠杆度较高的公司的经营收入波动性较大，贝塔系数也更高。调整公式为：

其中，βb：有经营杠杆的贝塔系数；

βu：无经营杠杆的贝塔系数。

但在估值实务中，由于固定成本/可变成本数据较难取得，使得经营杠杆调整的可操作性不强。一个可替代的方法就是采用营业利润的变动率与销售收入的变动率的比值作为经营性杠杆，公式为：

经营杠杆=营业利润变动率/销售收入变动率

（2）对财务杠杆进行调整

其他条件不变时，财务杠杆越大，贝塔系数越大。直观的影响是对债务的支付提高了净利润的方差。较高的财务杠杆在经济形势乐观时会增加收入，在经济衰退时会降低收入。调整公式如下：

其中，βL：有财务杠杆的贝塔系数；

βu：无财务杠杆的贝塔系数；

t：企业所得税率；

D/E：债务权益比。

[1]注册会计师全国统一考试辅导教材.财务成本管理.北京:中国财政经济出版社，2013.

[2](美)shanonP.Pratt,RogerJ.Grabowski.资本成本:应用和案例.北京:经济科学出版社，2013.

[3](美)Damodaran,Aswath.投资估价.北京:清华大学出版社，1999.