拟人机器人未知环境下稳定行走控制方法
肖 乐,殷晨波,谢从华
(1.常熟理工学院 计算机科学与工程学院,江苏 常熟 215500;2.南京工业大学 机械与动力工程学院,江苏 南京 210009)
1 引言
与其他机器人相比,拟人机器人具有更好的行动力,尤其是在不平整地面、斜坡、楼梯等复杂地面上行走时,拟人机器人具有无法比拟的优势.以往研究稳定行走的方法多是采用离线方式规划出满足特定要求的运动轨迹,直接将步态轨迹规划的理论用于步行实验[1-2],这样做的问题主要有三个方面:一是拟人机器人样机与机构设计结构总是有一定的误差,无法精确描述;二是机器人控制驱动系统在复现步态规划的理论结果时,总有一定的误差;三是机器人所在的环境,跟步态规划中的环境模型存在一定的偏差.也有机构采用各种在线修正算法来实现针对实际行走环境的稳定持续行走,步态通过上身位置与时间的对应关系进行调整,通过计算实际值与规划值之间的差值,所得误差经过简单快速处理后得出控制关节所需的扭矩,送回控制系统进行在线步态调节控制[3-7],但是由于地面条件与理想不符、系统模型不准确、运动学上未考虑的某些非线性因素、动力学方程中各矩阵的计算误差等原因,很难取得理想的步行控制效果,传统的维持机器人稳定控制技术大多是基于模型的控制方法,无法得到满意的轨迹跟踪效果,导致机器人不能按预先规划的姿态行走而摔倒[8].本文研究了机器人如何在未知环境下实时调整姿态,包括着地时间控制、落地位置控制和减振控制等方法,很好地控制了机器人的整个行走过程,使机器人时刻保持良好的稳定性.
2 调整控制方法
2.1 落地时间控制
在机器人的行走过程中,摆动腿的落地时间是在步态规划时所设置的.但是步态规划是在假定地面绝对水平的前提下进行的,它并不是机器人在真实行走中的落地时间.因此,有必要对落地时间进行补偿.传统的落地时间控制仅仅是在摆动腿根据步态规划的着地时间还没有和地面接触时,延缓行走步态流程.这种落地时间的滞后是由于地面的局部倾斜使得机器人向外倾斜所致.相反,如果机器人向内倾斜,它将在预期时间之前着地来防止跌倒,如图1所示.
在机器人向外倾斜的情况下,如果机器人不跌倒,那么只须延缓步态流程直到检测到摆动脚底的地面反作用力为止.然而,如果机器人是向内倾斜,就必须被提前检测到.在左右髋关节各装一个x方向的陀螺仪,可以通过角速度补偿落地时间.x方向的角速度由陀螺仪测得,左腿支撑期由左髋关节的陀螺仪测得,右腿支撑期由右髋关节的陀螺仪测得.
当角速度由正变负或由负变正时,往往发生在摆腿摆到最高点的时候.如图2所示,x轴代表时间,y轴代表陀螺仪的转速或摆动腿的摆动高度.为了方便起见,角速度用直线表示(见图3).在通常情况下,机器人身体侧向摆动的角速度会在A和B之间穿过x轴,因为骨盆侧向位移方向的改变与摆动腿达到最高点会有一个时间的滞后.如果机器人向内倾斜,则髋关节的角速度会在A点之前穿过x轴.这时,就需要提前降低摆动腿.其原理阐述如下:1.在步行周期的第一或第三个阶段,通过测量x方向的角速度得到角速度曲线穿过x轴的点.2.如果这个点在A和B之间,说明机器人不会提前着地.机器人可以规划的轨迹正常行走.3.如果这个点发生在比A点早△t的时间点,就使摆动腿提前△t的时间着地.
用这种方法能够优化机器人的着地时间,使机器人每一步的落地时间都是最佳时间,机器人就能稳定行走.

图1 机器人倾斜情况

图2 髋关节角速度和摆动腿轨迹

图3 落地时间控制
2.2 落地位置控制
和落地时间相似,落地时间补偿也很重要.机器人的落地时间和落地位置在机器人的行走过程中是很重要的两个因素,因为机器人行走最终实现的就是这两个因素.首先考虑人类的行走,落脚点是连续变化的.这一现象表明人们通过使用前庭器官来产生到达期望落地点所需的角动量.例如,如果落地角速度太大,那么我们会把步子跨大点,使落地点远离身体重心来减小着地时的角速度.同样的,拟人机器人也需要通过传感器的反馈控制对预期着地点进行调整,优化实际的落地位置.我们可以通过角动量在落地前补偿着地位置,使得机器人的摆动腿在合适的位置着地.
图4是机器人在着地前和着地后的状态.公式(1)用冲击模式来表示机器人的落地模式.

其中,ωBL是落地前瞬时的角速度,ωAL是落地后瞬时的角速度,I是相对于支撑点的惯性矩,M是摆动腿开始着地时作用于踝关节的力矩,Δt是M的作用时间,IωAL是落地后瞬时的期望角动量,IωBL是落地前瞬时测得的角动量.因此,有必要用 MΔt对IωAL进行调节,因为IωBL是随着机器人的行走而变化的.公式(1)可以写成如下形式:
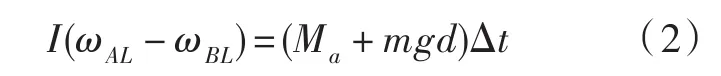
其中,Ma是摆动脚刚开始落地时由地面反作用力作用在踝关节的力矩,mgd由重力作用在踝关节的力矩.因此,落地点d,也就是距离身体中心的距离可由下式得到:
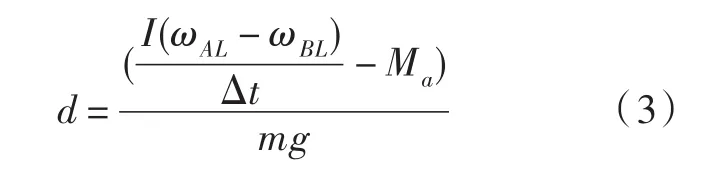
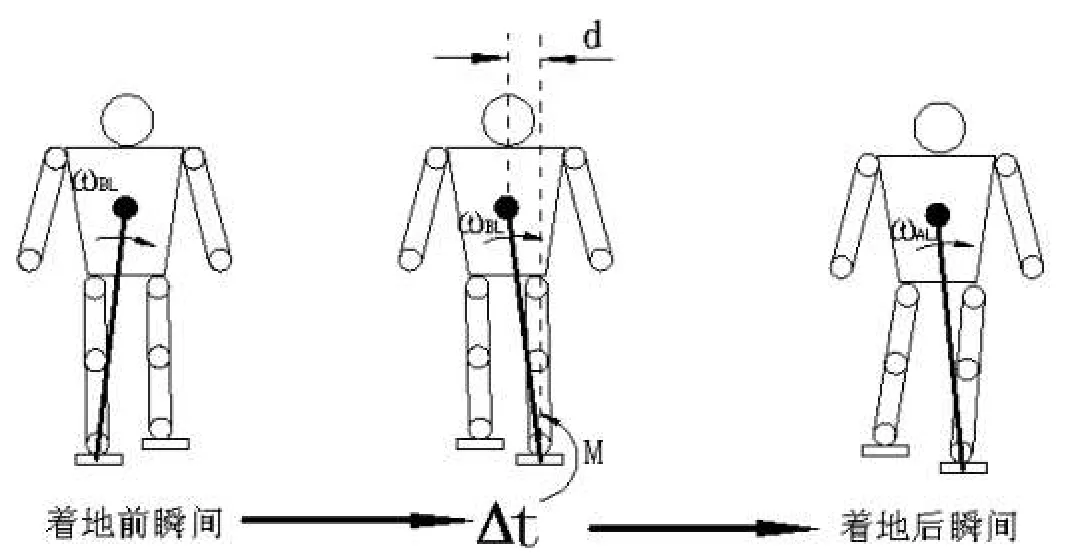
图4 落地位置控制
然而,实际上d是由步态规划所决定的.如果我们把预期的落地点记为dpre,那落地点的补偿量就可由d和dpre之差乘上一个比例增益kp得到.最终的落脚点dfinal就可以由dpre加上这个补偿量得到.

2.3 减振控制
当机器人行走的时候,摆动腿会有一定的振动.这是由于腿和盆骨之间的框架会有一定的偏斜,而且减速齿轮存在很小的齿侧间隙.这个振动量并不大,但会影响到落脚点精度的控制.如果落地点控制的精度超出了±3 mm的范围,落地点控制器将不能很好地发挥作用.因此对落地点位置控制来讲,减振是必需的.
图5是摆动腿的数学模型,u是输入的髋关节角度,θ是实际髋关节角度,m是脚的质点,l是从质点到髋关节的距离,k是弹簧的扭转刚度.系统的运动方程可以表示为

图5 摆动腿数学模型

传递函数可以表示为

以上的传递函数是一个在拉普拉斯域的虚轴上有两个极点的边界稳定系统.通过静态单脚支撑期的摆动腿的三个实验可以求得振动周期,从而得到k/ml2.
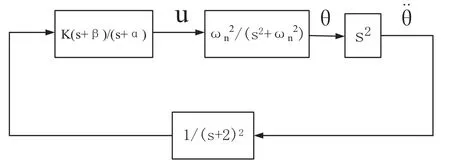
图6 减振控制框图
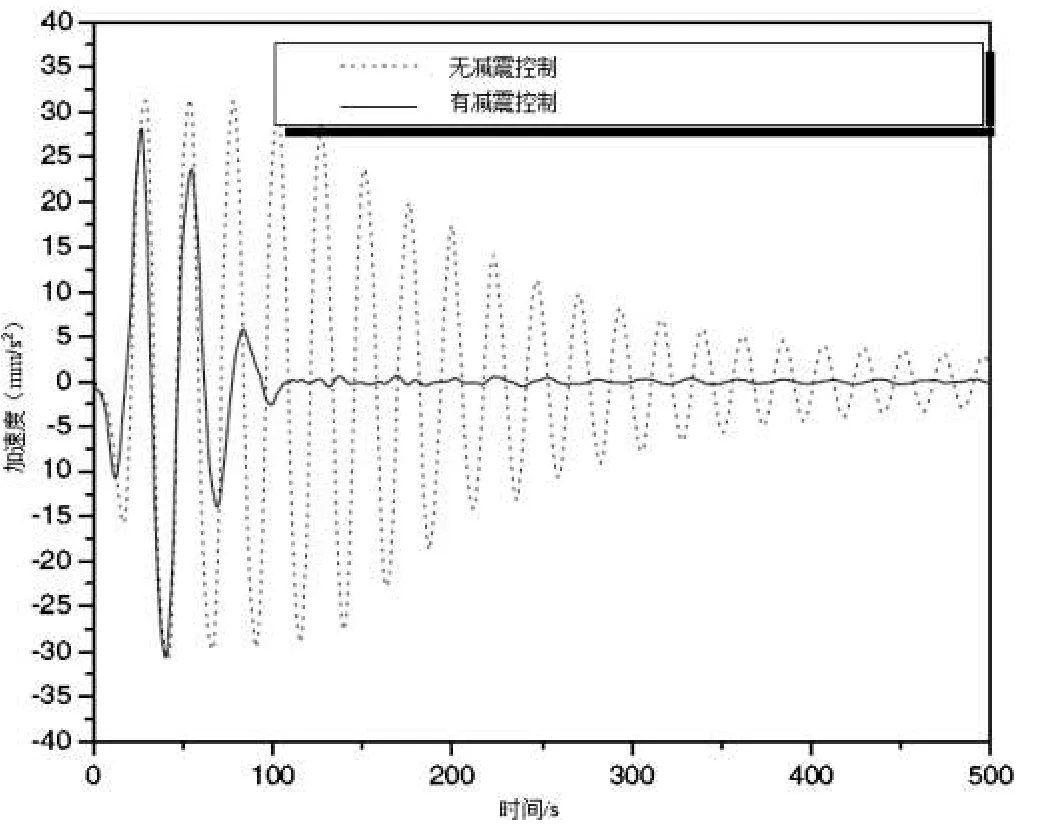
图7 摆动腿的自由振动响应
3 结束语
本文对拟人机器人双足稳定行走控制方法进行了深入研究,提出拟人机器人在复杂环境中如何通过落地时间控制、落地位置控制和减振控制等方法,使机器人获得新的支撑区域,恢复稳定,提高稳定行走能力,为实现拟人机器人实时控制奠定了基础.
[1]Harada K,Kajita S.Real-Time Planning of Humanoid Ro⁃bot's Gait for Force Controlled Manipulation[C].New Or⁃leans:Proceedings of the 2004 IEEE International Confer⁃ence on Robotics and Automation,2004:616-622.
[2]Eaton M,Thomas J,Davitt.Evolutionary Control of Bipedal Locomotion in High Degree-of-freedom Humanoid Robot:First Steps[J].Artificial Life and Robotics,2007 11(1):112-115.
[3]付根平,杨宜民,陈建平,等.基于ZMP误差校正的拟人机器人步行控制[J].机器人,2013,35(1):39-44.
[4]J H Kim,J H Oh.Walking Control of the Humanoid Platform KHR-1 based on Torque Feedback Control[C].New Orleans:Proceed⁃ings of the 2004 IEEE International Conference on Robotics and Automation,2004:623-628.
[5]陈磊,张国良,张维平,等.基于模糊控制的拟人机器人零力矩点在线调整[J].计算机应用,2013,33(SI):298-300.
[6]Napoleon,Nakaura S,Sampei M.Balance Control Analysis of Humanoid Robot based on ZMP Feedback Control[C].Lausanne:Pro⁃ceedings of the 2002 IEEE/RSJ International Conference on Intelligent Robots and System,2002:2437-2442.
[7]肖乐,常晋义,殷晨波.仿人机器人稳定性分析[J].常熟理工学院学报,2011,25(2):109-112.
[8]胡凌云,孙增圻.拟人机器人步态控制研究方法综述[J].计算机研究与发展,2005,42(5):728-733.

