六维力传感器薄板受迫振动分析
董跃龙,许德章
(安徽工程大学 a.机械与汽车工程学院;b.先进数控和伺服驱动技术实验室,安徽 芜湖 241000)
六维力传感器薄板受迫振动分析
董跃龙,许德章
(安徽工程大学 a.机械与汽车工程学院;b.先进数控和伺服驱动技术实验室,安徽 芜湖 241000)
目前弹性体的解耦大多以静态实验标定的方法求解,而缺少对弹性体建模的理论分析。以六维力传感器弹性体中的上E型膜为研究对象,根据其结构和约束条件建立力学模型,通过薄板弯曲理论推导出上E型膜在仅受Z方向载荷FZ时受迫振动过程中任一瞬时的动扰度表达式,并求出动态应变输出。仿真实验表明理论推导与实际情况较吻合。
六维力传感器;耦合;圆形薄板;薄板弯曲理论
六维力传感器是智能机械中的重要部件,用于检测三维空间力和力矩信息,应用广泛。由于现有的六维力传感器弹性体大都采用组合梁结构,当它仅受一个方向载荷作用时,其对应方向有力的输出,而在其他方向也有耦合力的输出,这就加大了弹性体解耦的困难度。目前对六维力传感器的研究大多以静态标定为主,通过实验标定法求得耦合矩阵从而实现静态解耦,而实际应用中传感器大多用来对动态实时信息的检测,因此对其弹性体的动态解耦研究更加重要。本文以双E型六维力传感器中的上E型膜为研究对象,基于薄板振动力学和弯曲理论,建立力学模型,采用解析法对圆形薄板进行受力分析,选取前一阶振型函数,推导出Z方向动载荷FZ激励下的动态应变输出,并进行了仿真实验,结果表明理论推导与实际情况较吻合。
1 弹性体结构
本文的实验对象是双E型六维力传感器,其结构如图1所示。弹性体结构主要包括矩形薄板4、上E型膜3和下E型膜6,应变片主要贴在其表面,而其他结构均看作刚体。上、下E型膜的各参数见表1。
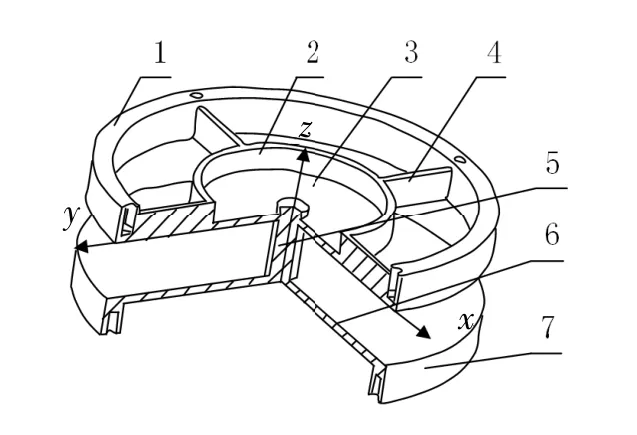
图1 六维力传感器结构示意图

表1 上、下E型膜的相关参数
2 弹性体受力分析
对弹性体Z方向施加载荷时,动载荷施加在外传力环的4个加载帽上,通过矩形薄板传递到内传力环,再由内传力环施加在上E型膜的外边沿,最后经中间传力环将上E型膜的受力传递到下E型膜,载荷施加方式如图2所示。由于上、下E型膜的结构类似,且中间支柱为刚体,为了避免重复讨论,本文只对上E型膜的受迫振动问题进行分析。

图2 六维力传感器施加载荷图
上E型膜的模型为均质等截面的圆形薄板,受Z方向动载荷作用时,上E型膜沿垂直于其平面的方向做弯曲受迫振动,满足薄板受迫振动理论的要求,故将上E型膜简化成外边界自由、内边界固定的圆形薄板模型,采用薄板受迫振动理论进行应力应变求解。
3 弹性体振动分析
根据薄板振动力学和弯曲理论,薄板在极坐标下的受迫振动微分方程可表示为

将(1)式右端的外加动载荷写成振型函数级数形式,即
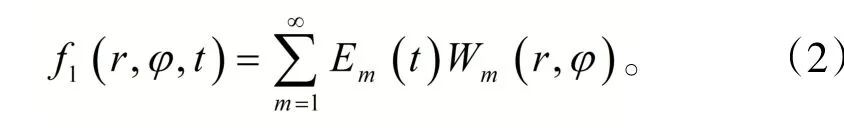
(2)式中的振型函数已经计算出,则方程(1)的解可表述为

将 (2)式及(3)式代入方程(1)中,整理得
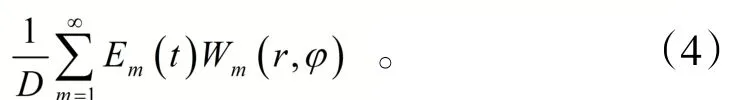
此方程为无阻尼时受迫振动微分方程,其通解可写成
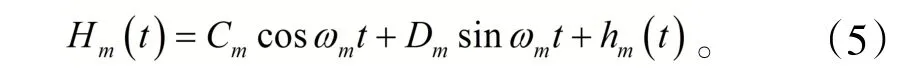
其中 为方程的特解。这样,圆形薄板受迫振动
过程中任一瞬时的动扰度可写成

根据零初始条件,可求出对应系数,从而可得上E型膜受迫振动过程的动扰度表达式为
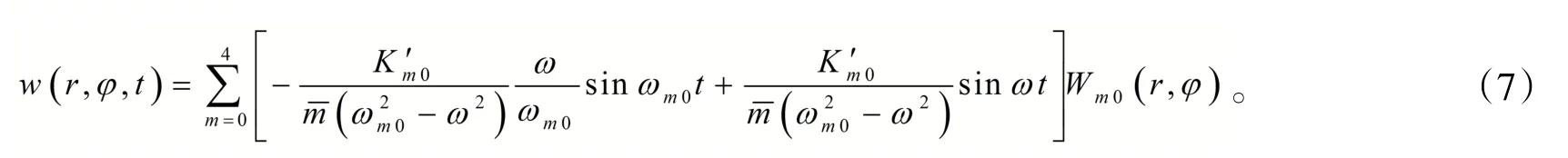
在对振型函数的选取中,理论上是阶数取的越高所得精度也越高,而实际中计算复杂度随阶数增加而加大,一般取前四阶即可满足工程要求。上E型膜固有频率及振型函数见表2。

表2 上E型膜固有频率及振型函数

将计算的各项参数代入(8)式,通过MATLAB软件可求解出上E型膜的动扰度为
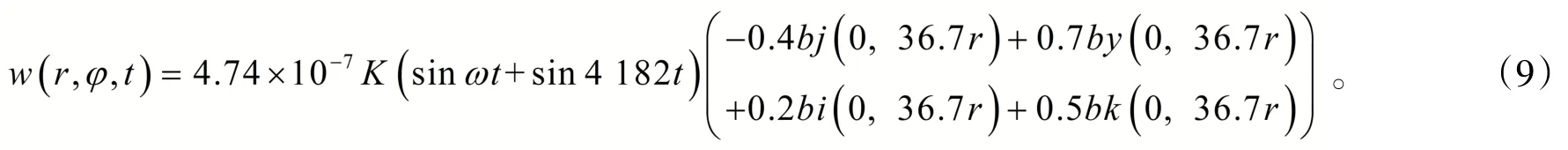
根据弹性力学和薄板弯曲理论可知,弹性体在上述受力作用下的应变输出以、、为主,又因为圆
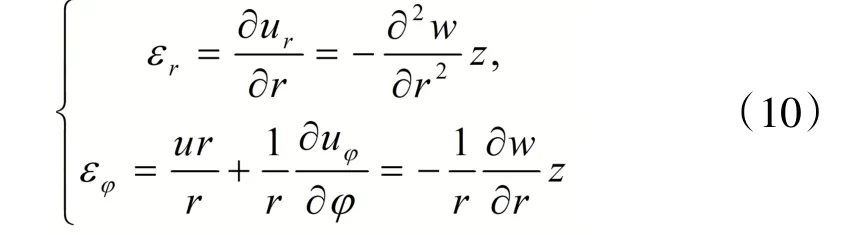
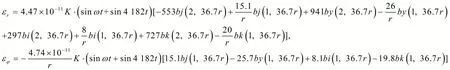
根据上述计算结果,进行仿真实验。由上E型膜表面的径向线应变和周向线应变分析可知,应变的位置变量取决于r、 φ 。取激励力的幅值K=1,在实际应用中机械手的工作带宽范围内选取激励频率20、35和 50 Hz,仿真出上E型膜受迫振动的径向线应变和周向线应变的空间图,如图3所示。从图3波形的起伏周期可知,上E型膜的振动频率随激励频率增加而增加,与实际情况相吻合。
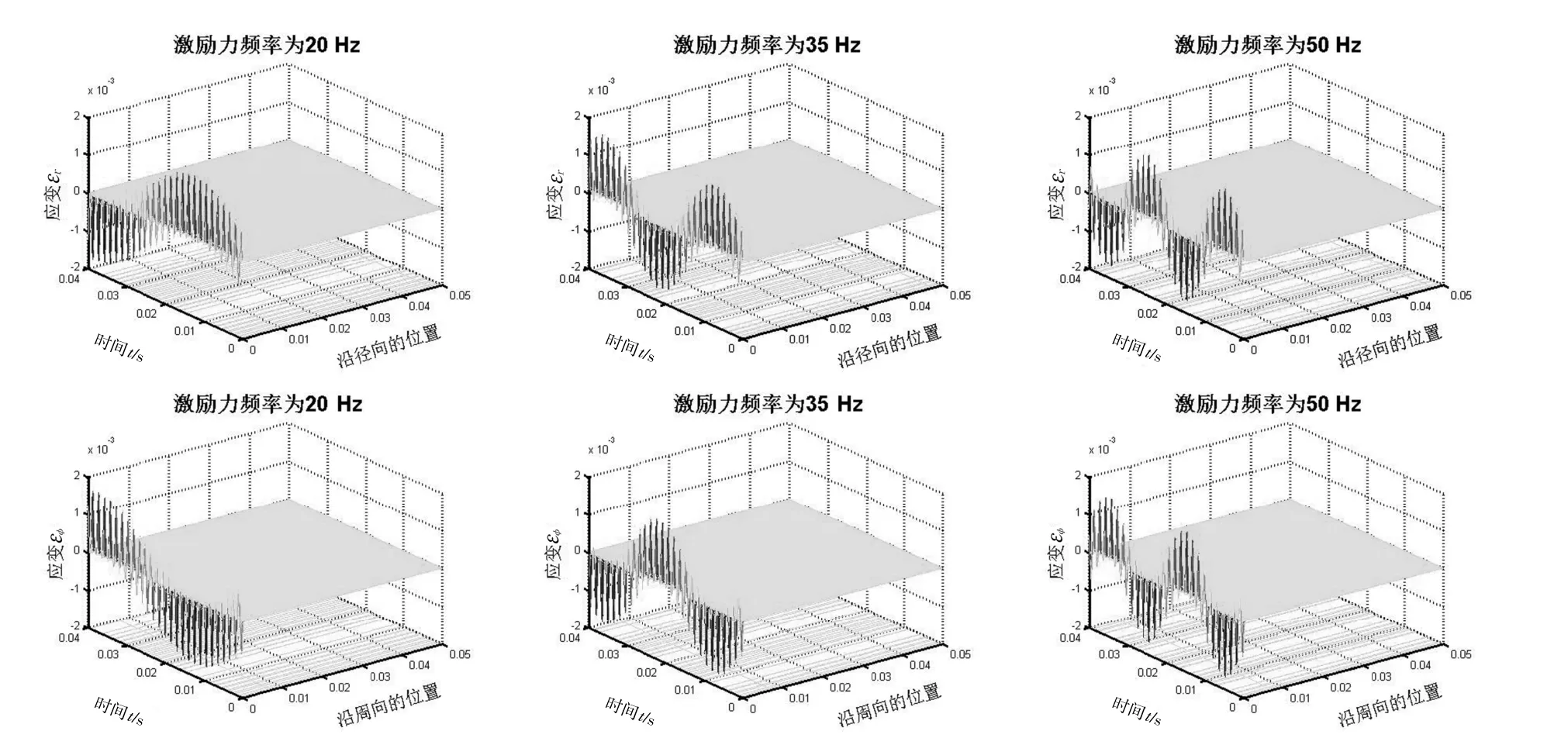
图3 上E型膜动态输出仿真
4 结论
本文以上E型膜为研究对象,根据其结构特征和边界条件建立力学模型,通过薄板弯曲理论推导出上E型膜在仅受Z方向载荷FZ时受迫振动过程中任一瞬时的动扰度表达式。取前一阶固有频率和振型函数对计算结果简化,从而求出简化后的动态应变输出,并对输出进行了实验仿真,仿真结果与实际情况较吻合。
[1] 许德章,吴仲城,葛运建,等.机器人六维腕力传感器耦合矩阵的确定与摄动分析[J].仪器仪表学报,2005(1):75-81.
[2] 姚智慧,张付祥.机器人六维力传感器研究概况及发展预测[J].广东自动化与信息工程,2002(3):7-9.
[3] 倪振华.振动力学[M].西安:西安交通大学出版社,1986:338-388.
[4] 徐芝纶.弹性力学:下册[M].北京:高等教育出版社,2006:50-54.
[5] 汪志红.电阻应变片式六维力传感器弹性体力学特性的研究[D].芜湖:安徽工程大学,2013.
[6] 谢黎峰,许德章.双E型六维力传感器矩形梁强迫振动分析[J].井冈山大学学报,2014(2):61-66.
[7] LIANG Q K, ZHANG D, SONG Q J, et al. Design and Fabrication of a Six-dimensional Wrist Force/Torque Sensor Based on E-type Membranes Compared to Cross Beams[J]. Measurement, 2010(43):1702-1719.
【责任编辑 黄艳芹】
The Forced Vibration Analysis of Thin Plates of Six-axis Force Sensor
DONG Yuelong, XU Dezhang
(a. School of Mechanical and Automotive Engineering; b. Advanced Numerical & Servo Technology, Anhui Polytechnic University, Wuhu 241000, China)
At present, elastic decoupling of six-axis force sensor is mostly achieved by the static calibration experiment, but there are few analysis of elastic body modeling theory. Taking E-type membrane of six-axis force sensor as study object, according to its structure feature and boundary conditions for the establishment of mechanical model, through the thin plate bending theory, this paper deduced the dynamic disturbance degree expression of E-type membrane in any instantaneous process of forced vibration, only by the dynamic load FZin Z direction effect, and gave the dynamic linear strain and simulation experiment. This paper provided theoretical and data foundation for the subsequent elastomer dynamic decoupling .
six-axis force sensor; coupling; circular thin plate; thin plate bending theory
O326
A
2095-7726(2015)03-0037-03
2014-11-10
国家自然科学基金项目(51175001);安徽省自然科学基金项目(11040606M144)
董跃龙(1989-),男,江苏建湖人,硕士研究生,研究方向:机器人与信息感知。

