Double设计在对称化L2-偏差下两个下界的比较

雷轶菊

（新乡学院 数学与信息科学系，河南 新乡 453003）

Double设计在对称化L2-偏差下两个下界的比较

雷轶菊

（新乡学院 数学与信息科学系，河南 新乡 453003）

从列平衡的角度出发，将设计的中心化L2-偏差、对称化L2-偏差、可卷L2-偏差分别用二次型和均衡模式表示，可分别得到两个下界， 它们都适合用来评价正交设计的均匀性。以double设计的对称化L2-偏差为例，证明了这两种方法算出的下界是相等的。

Double设计；对称化L2-偏差；下界

在构造2-水平部分因子设计，特别是那些分辨度为IV的设计中，doubling是一种简单却很有用的方法。假定，则称是的double。若是一个处理个数为n，具有1和-1两个水平的k个因子的设计， 定义每一行为一个水平组合，那么定义了一个设计，其处理大小和因子个数都是的两倍。最初，R. L. Plackett和J. P. Burman用doubling方法构造了正交主效应设计。CHEN H. G.和CHENG C. S.［2］用doubling方法将一个分辨度为IV的2-水平正规部分因子设计构造成分辨度仍为IV的double设计。XU H. Q.和CHENG C. S.［3］讨论了double设计中补设计的一般理论问题。在文献［2-3］中讨论构造最大的二水平部分因子设计时，doubling方法起了重要的作用。

有关double设计方面的研究，涉及的都是因子设计方面的一些成果。笔者和覃红［4］从均匀性的角度对double设计的性质作了讨论，分别在列平衡和行平衡下给出了double设计在对称化L2-偏差下的两个下界，并指出这两个下界分别对衡量哪种设计的均匀性是有效的。FANG K. T.等［5-6］从列平衡出发，分别用两种计算方法得到了两个下界，且都适合用来评价正交设计的均匀性。既然这两种方法考虑的都是列平衡，那么由这两种方法得到的下界有何关系呢？到目前为止，这方面的研究还未见报道。在本文中，笔者以double设计的对称化L2-偏差为例，证明了用两种方［1］法算出的下界是相等的。

1 预备知识

， （1）

经过简单代数计算，由（2）式可得

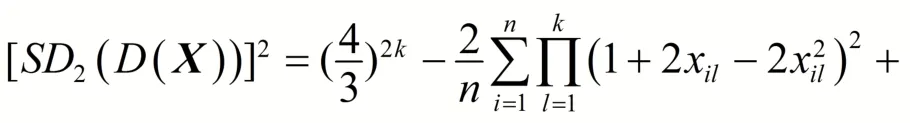
2 Double设计在对称化L2-偏差下的两个下界的比较

定理2中的下界是基于列平衡的考虑算出的，和定理1中的下界一样，都适合用于评价正交设计的均匀性。下面，证明这两个下界实际上是相等的。

证明：只需证明

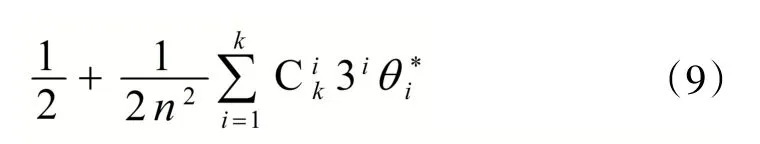
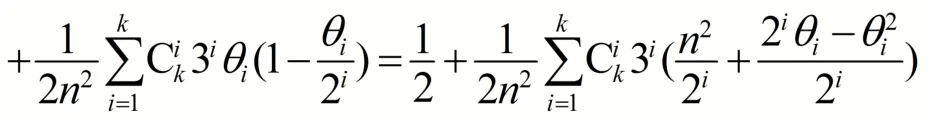
综上所述，有（9）式左边=（9）式右边，即（8）式成立。

［1］ PLACKETT R L, BURMAN J P. The Design of Optimum Multi-factorial Experiments［J］. Biometrika, 1946, 33: 305-325.

［2］ CHEN H G, CHENG C S. Doubling and Projection: A Method of Constructing Two-level Designs of Resolution IV［J］. Ann Statist, 2006, 34: 546-558.

［3］ XU H Q, CHENG C S. A Complementary Design Theory for Doubling［J］. Ann Statist, 2008, 36: 445-457.

［4］ 雷轶菊，覃红. Double设计在对称化L2-偏差下的均匀性［J］.华中师范大学学报（自然科学版），2010，44，369-372.

［5］ FANG, K T, MUKERJEE R. A Connection Between Uniformity and Aberration in Regular Fractions of Two-level Factorials［J］. Biometrika, 2000, 87: 193-198.

［6］ FANG K T, LU X, WINKER P. Lower Bounds for Centered and Wraparound L2-discrepancies and Construction of Uniform Designs by Threshold Accepting［J］. J Complexity, 2003, 19: 692-711.

［7］ HICKEMELL F J. A Generalized Discrepancy and Quadrature Error Bound［J］. Mathematics of Computation, 1998, 67: 299-322.

【责任编辑 王云鹏】

Comparison of Two Lower Bounds for the Symmetric L2-discrepancy of Double Designs

LEI Yiju
（College of Mathematics and Information Science, Xinxiang University, Xinxiang 453003, China）

In view of the column balance, the centralized L2-discrepancy, symmetrized L2-discrepancy and rollable L2-discrepancy of a design could be respectively represented with quadric form and balance pattern； then two lower bounds could be respectively obtained. They were suitable for evaluating uniformity of the orthogonal designs. This paper proved in the case of the symmetric L2-discrepancy of double designs the lower bounds by two kinds of calculation methods are equal.

double design； symmetrized L2-discrepancy； lower bound

O212.6

A

2095-7726（2015）03-0001-03

2015-01-06

雷轶菊（1976-），女，湖北荆州人，讲师，硕士，研究方向：试验设计。