一类小世界振子网络的滑模控制混沌同步

常 娟，李 亮，毛北行

（郑州航空工业管理学院 数理系，河南 郑州450015）

一类小世界振子网络的滑模控制混沌同步

常 娟，李 亮，毛北行

（郑州航空工业管理学院 数理系，河南 郑州450015）

基于滑模控制理论研究了一类小世界振子网络的混沌同步问题，并根据Lyapunov稳定性理论给出了系统渐近同步的充分性条件，给出的数值算例表明了该方法的有效性。

小世界网络；滑模；混沌同步

混沌同步已广泛应用于控制学科和网络、医学、生物学等领域［1–5］，秦卫阳等［6］研究了一类动力学系统的函数耦合混沌同步问题。在现实生活中，还存在着各种各样的复杂网络，人们在复杂网络方面的研究已取得了一些成果［7–14］。作为复杂网络重要分支的小世界网络也引起人们的注意［15–16］，周晶等［17］研究了具有时滞的小世界振子网络的稳定性，并给出了小世界网络稳定性的判定依据，但关于小世界网络混沌同步的研究还比较少。在本文中，我们基于滑模控制理论研究了一类小世界振子网络的混沌同步问题，并根据Lyapunov稳定性理论得到了系统渐近同步的充分性条件。

1 主要结果

考虑如下小世界振子网络

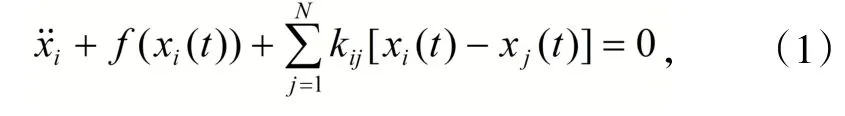
其中，xi表示第i个振子的位移， kij表示振子i与振子j之间的耦合强度。另外，kij还满足以下条件：当振子i与j（i≠j）之间存在连接时， kij＞0，且kij=kji；当振子i与j（i≠j）之间不存在连接时，kij=0。

（1）式可转化为

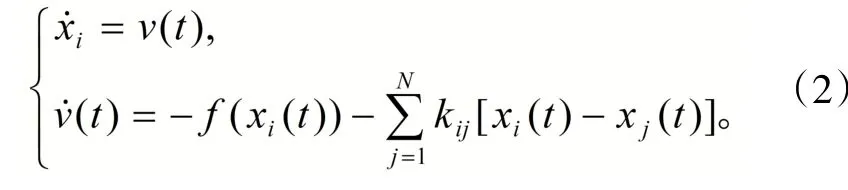
（1）式对应的响应系统为

系统（3）可转化为

定义系统（1）和系统（3）的误差为eil（t）=yi（t）-xi（t），则（3）式与（1）式相减得到误差系统为

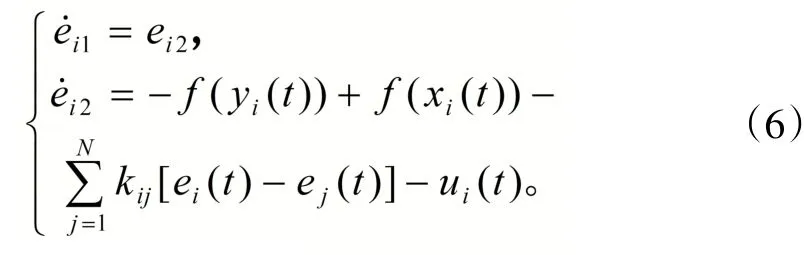
柬埔寨在分析框架中的定位为L型组合(积极配合)。目前柬埔寨的文化影响力偏弱，不仅对外文化推广存在难度，其国内的文化事业发展也比较薄弱，对国际文化援助具有较高需求。而柬埔寨的地缘环境又令其十分重视中国对保障国家生存发展的作用，对中国文化的传播也持有欢迎接纳的态度。因此柬埔寨在同中国发展文化外交关系时主要采取了积极配合的行为。

考虑具有时滞的小世界振子网络

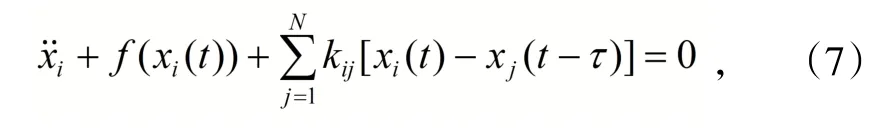
（7）式可转化为如下系统

（7）式作为驱动系统，其对应的响应系统可设为

系统（9）可转化为

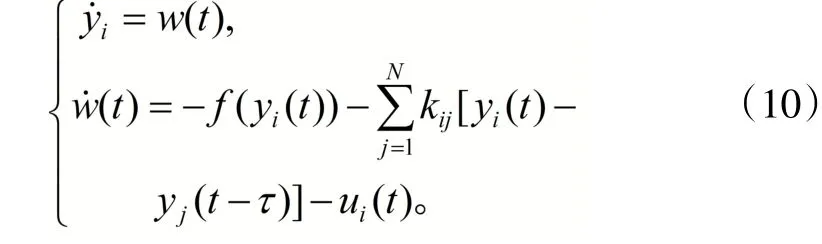
2 数值仿真

取定理1中的驱动系统为

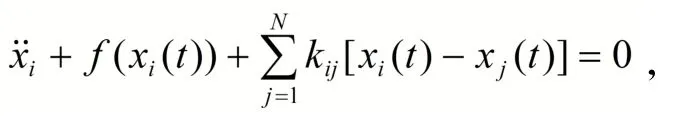
响应系统为

其中

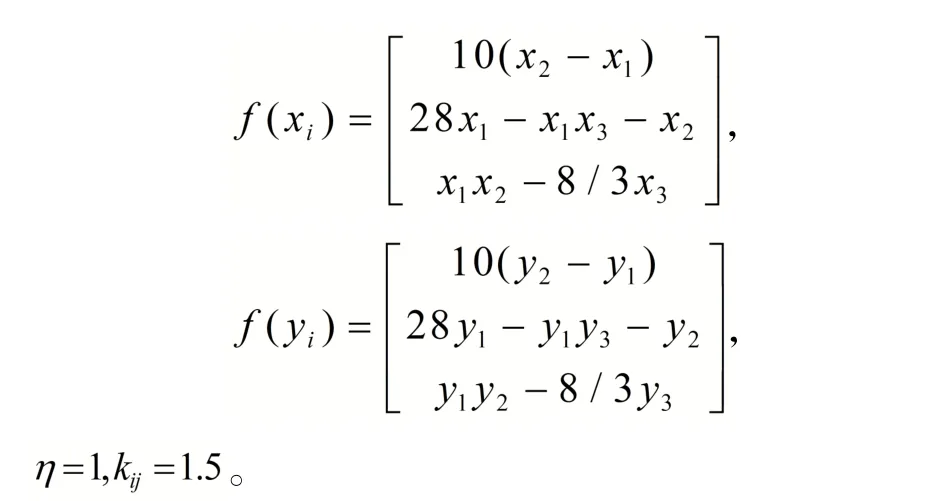
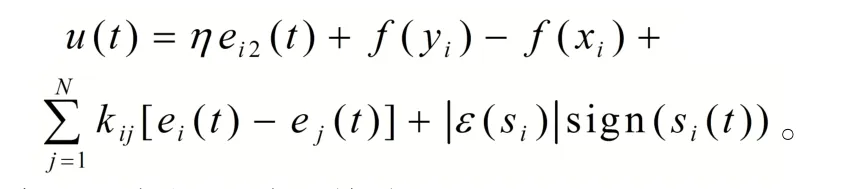
定理2中的驱动系统为

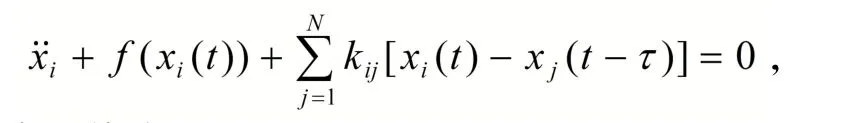
响应系统为

其中

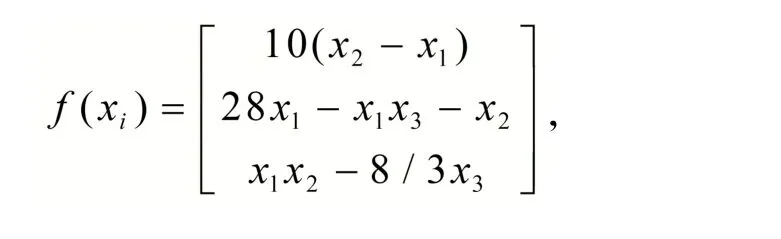
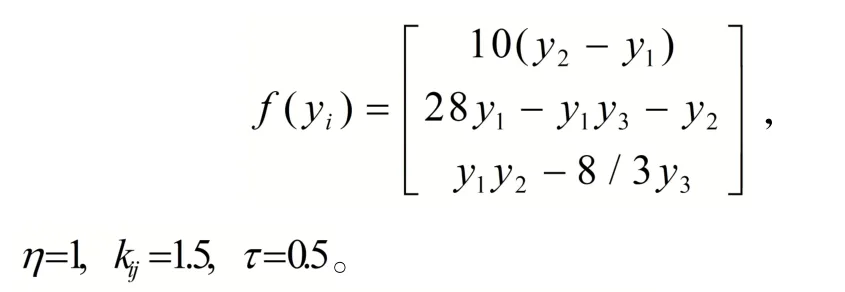
3 结束语

在本文中，我们基于滑模控制理论研究了一类小世界振子网络的混沌同步问题，并根据Lyapunov稳定性理论得到了系统渐近同步的充分性条件，给出的数值算例说明了该方法的有效性。

［1］ 李文林，宋运忠.不确定非线性系统混沌反同步［J］.物理学报，2008（1）：51-55.

［2］ 徐瑞平，高存臣.基于线性反馈控制的一类混沌系统同步［J］.中国海洋大学学报，2014（5）：114-120.

［3］ GASSARA H, EI HAJJAJI A, CHAABANE M. Observer-based Robust Reliable Control for Uncertain T-S Fuzzy Systems with State Time Delay［J］. IEEE Transaction on Fuzzy Systems, 2010, 18（6）: 1027-1040.

［4］ NIU Y, HO D W C. Robust Observer Design for Ito Stochastic Time-delay Systems Via Sliding Mode Control［J］. Systems Control Letters, 2006, 55（10）: 781-793.

［5］ 赵岩岩，蒋国平.一类输出耦合时延复杂动态网络故障诊断研究［J］.物理学报，2011（11）：2061-2066.

［6］ 秦卫阳，孙涛，焦旭东，等. 一类动力学系统通过函数耦合实现混沌同步［J］.物理学报，2012（9）：5021-5025.

［7］ 方洁，胡智宏，江泳.耦合混沌系统自适应修正函数投影同步［J］.信息与控制，2013（1）：39-45.

［8］ 吕翎，李纲，张檬，等.全局耦合网络的参数辨识与时空混沌同步［J］.物理学报，2011（9）：5051-5056.

［9］ 李德奎，张建刚.时滞和非时滞耦合的驱动响应动态网络的函数投影同步［J］.太原理工大学学报，2013（2）：162-168.

［10］ 卞秋香，姚洪兴.复杂网络的线性广义同步［J］.系统工程理论与实践，2011（7）：1334-1340.

［11］ LYU L, LI G, GUO Y. Generalized Chaos Synchronization of a Weighted Complex Network with Different Nodes［J］. Chinese Physics B, 2010, 19（8）: 5071-5077.

［12］ 毛北行，李巧利.Lurie混沌系统的有限时间同步问题［J］.四川师范大学学报（自然科学版），2014（4）：497-500.

［13］ 邓玮，孙君曼，崔光照，等.基于非线性输入控制实现受扰混沌系统同步［J］.系统工程与电子技术，2010（4）：837-841.

［14］ MEI J, JIANG M H, WANG J. Finite-time Structure Identification and Synchronization of Drive-response Systems with Uncertain Parameter［J］. Commun Nonlinear Sci Numer Simulat, 2013（18）: 999-1015.

［15］ WATTS D J, STROGATZ S H. Collective Dynamics of Small World Networks［J］. Nature, 1998, 393（4）: 440-442.

［16］ NEWMAN M E J, WATTS D J. Scaling and Percolation in the Small-world Network Model［J］. Phys Rev, 1999, 60: 7332-7342.

［17］ 周晶，于东元，徐旭.具有时滞的小世界网络稳定性［J］.吉林大学学报（理学版），2015（1）：5-8.

【责任编辑 王云鹏】

Sliding Mode Chaos Synchronization of a Class of Small World Vibrator Network

CHANG Juan, LI Liang, MAO Beixing
（Department of Mathematics and Physics, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou 450015, China）

The study of chaos synchronization for a class of small world vibrator network is based on sliding mode theory. Combined with Lyapunov stability theory, the conclusion is drawn that the system is chaos synchronized under appropriate controlling law and switching function. The simulated numerical example of chaotic system in the paper verified the effectiveness of the proposed method.

small world network； sliding mode； chaos synchronization

O482.4

A

2095-7726（2015）03-0004-03

2014-11-23

国家自然科学基金项目（51072184）；国家自然科学基金数学天元基金项目（11226337）；中国航空工业第一集团公司航空科学基金项目（2013ZD55006）；河南省高等学校青年骨干教师资助计划项目（2013GGJS-142）；河南省科技厅基础与前沿研究计划项目（142300410410）；郑州航空工业管理学院青年基金项目（2014113002）

常娟（1978-），女，河南温县人，讲师，硕士，研究方向：复杂网络与混沌同步。