本体稀疏向量迭代计算算法
高 炜
(云南师范大学 信息学院,云南 昆明 650500)
本体稀疏向量迭代计算算法
高 炜
(云南师范大学 信息学院,云南 昆明 650500)
用机器学习方法得到本体函数时,需要将每个本体概念所对应的信息用一个p维向量来表示。在很多应用背景下,由于p值很大而导致计算量庞大。通过稀疏向量的学习来得到本体函数,利用块方法设计一种迭代计算算法进而得到稀疏向量。将该算法应用于生物基因GO本体和物理教育本体,并将实验结果与已有算法的结果作对比,验证了算法在生物基因领域的相似度计算和在物理教育学领域建立本体映射上有较高的效率。
本体;相似度计算;本体映射;稀疏向量
近年来,各种机器学习技术被广泛应用于本体相似度计算和本体映射中。文献[1]将排序学习技术应用于本体相似度计算,进而得到对应的本体映射策略。文献[2]用图学习的方法得到本体相似度计算算法。文献[3]和[4]则是通过优化正则化模型得到本体函数f,并将此方法分别应用于本体相似度计算和本体映射算法。由于大多数本体图都是树形结构,文献[5]提出了k-部排序半监督学习算法。算法充分利用本体图的结构特征,并将半监督算法和k-部排序相结合应用于本体相似度计算。相关本体算法的理论分析可参考文献[6-7]。
本体模型可用图结构G =(V,E)来表示,本体学习算法的目标是得到一个本体(得分)函数f:V→R。该本体函数将整个本体图映射到实直线上,图中每个顶点都映射成实数。因此,可通过两顶点所对应的实数在实数轴上的距离来判定两顶点对应概念之间的相似度。
本文利用块技术提出用一种迭代计算方法得到本体稀疏向量,通过本体稀疏向量间接得到本体函数,再通过本体函数计算顶点对应的实数在数轴上的距离,最后确定它们之间的相似度。本文主要内容是:首先介绍算法的设计思想和具体的执行步骤;然后,将本体稀疏向量计算算法应用于生物基因“GO”本体和物理教育学本体,并将实验数据与通过已有算法得到的数据进行对比,进而说明本文算法在生物基因领域本体相似度的计算和物理教育学领域本体映射的构建上有较高的效率。
1 新算法描述
1.1 算法框架
本体图中的每个顶点都代表一个概念,该概念的名称、属性、结构、语义等信息都可用一个p维向量来表示。设v=(v1,v2,…,vp)是顶点v对应的向量。本体学习算法的目标是得到最优本体(得分)函数f:V →R,顶点对应概念之间的相似度通过顶点对应实数在数轴上的距离来衡量。此类算法的本质是降维,用一维向量来表示p维向量,即所要学习的本体函数f是一个降维函数f:Rp→R。
由于本体概念对应的向量不但包含了这个概念的所有语义信息,而且包含了这个概念在本体图中的邻域和结构信息,因此,在很多应用中,向量的维度会非常大,比如在生物学本体中,所有的基因信息都包含在一个向量中。此外,本体图众多的顶点数也使得它的结构变得错综复杂,比如地理信息系统本体,这可能会导致本体相似度计算的复杂度非常高。但在很多实际应用中发现,真正对概念之间相似度起决定作用的往往是向量中的少部分分量,比如:在生物遗传本体应用中,导致某类遗传疾病的恰恰是很少几个基因,而其他大部分基因与该病无关;在地理信息系统本体的实际应用中,如果某个地点发生交通事故,那么需要寻找的是和事发地点距离最近的医院,而不是附近的商场和娱乐场所,即要寻找的是本体图中符合特定要求的顶点(概念)。因此,下面将稀疏向量学习算法引入到本体相似度算法中。
在实际应用中,本体函数可通过稀疏向量作如下表示:

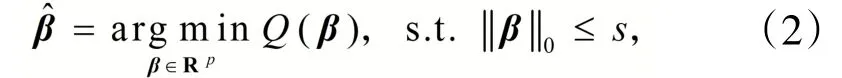
1.2 分块和编码技术的运用
设系数的指标集I={1,2,…,p},对于任意稀疏子集∪I,都分配一个代价函数cl()表示的编码长度(在计算机程序中表示需要的字节数)的上界。由信息理论可知,存在编码等价于。设空集的编码长度为0,则定义在I的子集上的代价函数cl()称为编码长度。如果成立,则的结构稀疏编码复杂度定义为c() =cl()+||。若成立,则编码长度cl()称为次可加的。同样,若成立,则编码复杂度c()称为次可加的。根据定义,若cl()是次可加的,则对应的c()也是次可加的。给定编码复杂度c(),则稀疏向量的结构稀疏编码复杂度定义为
下面引入块编码技术,这是一种在稀疏编码领域中常见的方法。所谓的块B是I的一个子集,并且设是若干个块的集合,满足,且每个单个元素的集合{i} (i∈I )属于。因为每个单个元素都是块集合中的元素(块),所以任意子集∪I都可以表示成块集合中若干个块的并。用cl0表示定义在上的代码长度,则有。对于任意B∈,定义。由于
因此,在∪I上的代价函数即为编码长度cl()=
由定义可知,块编码是次可加的。引入块的目的在于,在搜索算法中,可以通过搜索块取代原先搜索I的子集,同时每次迭代只增加一个块,而 B中包含的块是有限的,因此算法具有更高的计算效率。
1.3 稀疏向量的求解
以编码复杂度作为计算模型的限制条件,则(2)式可以写为

算模型中,(3)式可以写为

直接优化(4)式有很大的困难,因此下面给出本文的稀疏向量迭代计算方法。设比率用来衡量当编码复杂度增加后亏损项的减少量。设映射矩阵PF=VF
(VFTVF)-1VFT,其中VF是在信息矩阵V中取对应的列得到的矩阵。对于最小平方回归可作如下逼近:
从而在迭代过程中,选取满足如下条件的B(k):
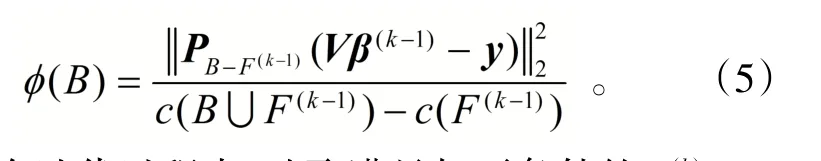
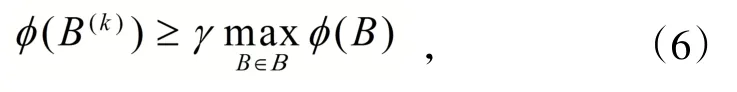
本体稀疏向量迭代学习算法如下:
输出:(k), β(k);
设初始项(0)
对k=1,2,…;
选择
满足(6)式;
设
2 实验
将本文得到的本体稀疏向量迭代计算算法应用于生物基因本体和物理教育学本体,来验证算法的有效性。先通过算法得到稀疏向量,再通过得到本体函数(两个实验均忽略噪声项的计算),然后根据本体函数f将顶点映射成实数,最后通过对应实数在数轴上的距离来判断两顶点对应概念之间的相似度。在具体操作过程中,令,同时y、V、B和s由领域专家给出。
2.1 本体相似度计算实验
第一个实验是采用http://www. geneontology.org网站构建的生物基因GO本体O1(其结构可参考图1)来验证算法的效率。生物基因GO本体的结构为树形,顶点被分成 “Biological process”、“Molecular function”和“Cellular component”三个分支。通过本体顶点相似度计算,可以了解不同分子功能、化学细胞结构和生物过程之间的相互关联,有助于生物学家了解基因、化学结构以及分子化学作用之间的关联信息。
除本文算法外,还将本体回归算法[8]、快速排序算法[9]和标准本体排序算法[1]分别作用于生物基因GO本体。用P@N[10]平均准确率来衡量实验结果的好坏,将这三种算法得到的P@N准确率与本文算法得到的P@N准确率进行对比。当N=3,5,10时,数据如表1所示。由表1可知,本文稀疏向量计算算法对于生物基因GO本体的效率明显高于其他三种算法。
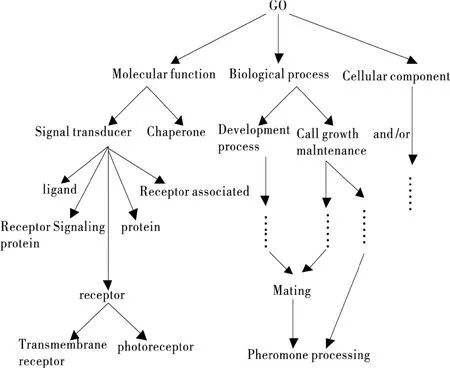
图1 GO本体O1
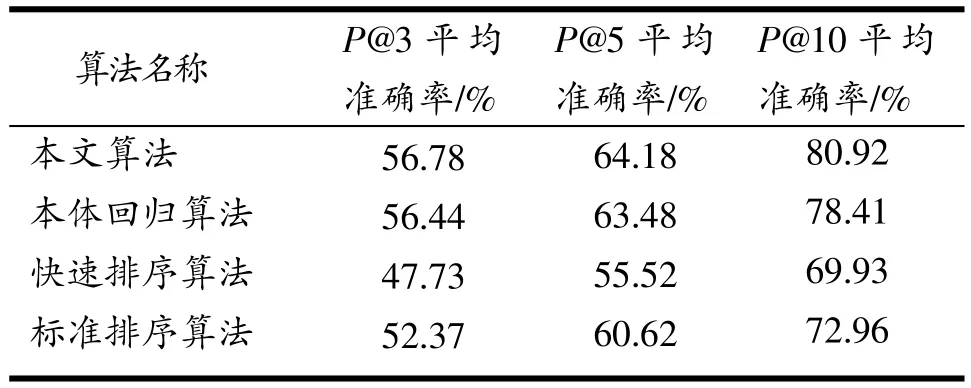
表1 实验1部分数据
2.2 本体映射实验
第二个实验是采用下面两个“物理教育”本体O2和O3来验证本文稀疏向量学习算法的效率。这两个本体都是将中学物理教育中的一些基本教学元素通过它们的从属关系串联成本体结构图。笔者通过计算,在这两个物理教育本体之间建立本体映射。即对于图2中的某个概念,在图3中寻找与该概念相似度高的顶点,然后作为映射结果返回;同样,对于图3中的某个概念,在图2中寻找与之相似度高的顶点,然后作为映射结果返回给用户。
此外,将本体回归算法、快速排序算法和标准本体排序算法分别作用于“物理教育”本体,然后将这三种算法得到的P@N准确率与本文算法得到的P@N准确率进行比较。当N=1,3,5时,数据如表2所示。

图2 “物理教育”本体O2

图3 “物理教育”本体O3

表2 实验2部分数据
由表2可知,本文稀疏向量学习算法在“物理教育”本体O2和O3间建立本体映射的效率明显高于其他三种算法。
3 结束语
作为一种结构化数据存储和表示模型,本体被应用于自然科学和社会科学的各个领域,比如制药学、地理信息系统、生物学和教育学等。当使用机器学习模型来获得本体函数时,需要将本体的信息数学化,即用一个多维向量来表示顶点的信息,而向量维数的庞大往往导致大计算量。
本文利用块技术提出一种迭代算法得到本体稀疏向量,进而通过本体稀疏向量来得到本体函数,最后通过本体函数得到顶点对应概念之间的相似度。实验数据表明,该方法对于生物基因领域的相似度计算和物理教育学领域的本体映射构建是有效的,也使生物基因GO本体的研究对制药学、生物学和医学都有重要的理论和应用价值;同时,有助于了解由物理教育学元素以不同的方式构成的不同结构图之间相互联系,从而帮助教学工作者进行物理教学元素的统筹及设计整体教学规划方案。
[1] 高炜,兰美辉.基于排序学习方法的本体映射算法[J].微电子学与计算机,2011(9):59-61.
[2] 高炜,梁立,张云港.基于图学习的本体概念相似度计算[J].西南师范大学学报(自然科学版),2011(4):64-67.
[3] 高炜,梁立.基于超图正则化模型的本体概念相似度计算[J].微电子学与计算机,2011(5):15-17.
[4] 高炜,朱林立,梁立.基于图正则化模型的本体映射算法[J].西南大学学报(自然科学版),2012(3):118-121.
[5] 高炜,梁立,徐天伟,等.半监督k-部排序算法及在本体中的应用[J].中北大学学报(自然科学版),2013(2):140-146.
[6] 高炜,张云港,梁立. Cs相似度函数下正则谱聚类的收敛阶[J].兰州大学学报(自然科学版),2011(2):109-111.
[7] 高炜,周定轩.与一般相似度函数相关的谱聚类的收敛性[J].中国科学:数学,2012(10):985-994.
[8] GAO Y, GAO W. Ontology Similarity Measure and Ontology Mapping Via Learning Optimization Similarity Function[J]. International Journal of Machine Learning and Computing, 2012, 2(2): 107-112.
[9] HUANG X, XU T W, GAO W, et al. Ontology Similarity Measure and Ontology Mapping Via Fast Ranking Method[J]. International Journal of Applied Physics and Mathematics, 2011, 1(1): 54-59.
[10] CRASWELL N, HAWKING D. Overview of the TREC 2003 Web Track[C]//Proceedings of the Twelfth Text Retrieval Conference, Gaithersburg, Maryland, November 18-21, 2003, NIST Special Publication, 2003: 78-92.
【责任编辑 梅欣丽】
Iterative Computation Algorithm for Ontology Sparse Vector
GAO Wei
(School of Information, Yunnan Normal University, Kunming 650500, China)
The information for each vertex should be expressed as a p dimension vector when we apply machine learning technology to ontology. In many applications, it leads to large computation cost since p is large. In this paper, the ontology function was obtained in terms of sparse vector learning. The optimal sparse vector was yielded via iterative computation algorithm based on block technology. The algorithm was applied to the GO and physical education ontologies, and the results from our algorithm were compared with results from previous algorithms. It showed that the new algorithm had higher efficiency for calculating the similarity in biology gene field and for establishing the ontology mappings in physical education application.
ontology; similarity measure; ontology mapping; sparse vector
TP393.092
A
2095-7726(2015)03-0033-04
2015-01-01
国家自然科学基金青年科学基金项目(11401519)
高炜(1981-),男,浙江绍兴人,讲师,博士,研究方向:机器学习和图论。

