多通道联合控制数控振荡器的环路设计

王 前，胡彩波

（1. 北京航空航天大学 仪器科学与光电学院，北京 100191；2. 北京卫星导航中心，北京 100094）

多通道联合控制数控振荡器的环路设计

王 前1,2，胡彩波2

（1. 北京航空航天大学 仪器科学与光电学院，北京 100191；2. 北京卫星导航中心，北京 100094）

信号跟踪是卫星导航接收机的核心处理技术，提升跟踪处理性能可弥补卫星导航易受干扰和遮挡的固有不足，具有重要的应用前景。在分析信号跟踪和测量的基本原理上，利用误差估计关系建立了定位域和信号域的物理联系桥梁。通过抽象的跟踪环路传输模型，归纳出提升环路性能的技术途径，改变了传统环路相互独立的设计思路，利用加权最小二乘算法设计了多数据源联合控制数控振荡器的矢量化环路跟踪算法，并从理论和仿真实验两方面对算法的性能进行了全面的对比分析。结果表明，该方法在与普通接收机处理复杂度相当的情况下，可提高环路在弱信号环境下的处理能力，多通道联合辅助某一弱信号通道时可提高6 dB的增益，多通道联合跟踪相对比各通道独立工作可提高3 dB的增益。

卫星导航；数控振荡器；最小二乘；信号跟踪

环路跟踪作为GNSS接收机的核心部分，长期以来一直是研究的重点。在可见卫星数充足、信号质量较好的条件下，接收机能够稳定准确的跟踪卫星信号。但是，在很多特定情况下信号强度会变得很微弱，可见星的数目也会减少，有时甚至受到动态Doppler或者干扰的影响，这时普通的信号跟踪性能往往不能满足这类恶劣环境的要求，造成信号测量误差增大，严重时甚至会引起信号失锁乃至定位失败。因此，提高环路跟踪的准确性和鲁棒性是很重要的研究方向。

目前，主要存在三种提高环路跟踪性能的方法。第一，改变环路设计时的重要参量，如环路带宽[1-3]、积分时间以及鉴相器或者鉴频器的判决方法等。这类方法是最常用的环路优化方法，在某种程度上确实能提高环路的性能，但由于环路自身跟踪门限的限制，不能解决动态应力和热噪声两因素带来的矛盾，只能通过动态优化的方法在两者间求得相对的折中[1-3]。第二种借用INS（Inertial Navigation System）器件输出的Doppler信息辅助环路跟踪，从而提高接收机在恶劣环境下的跟踪能力。随着INS器件生产工艺的发展，这类方法也逐步得到广泛应用[4-7]。第三类采用矢量跟踪的方法提高环路性能，通常包括DLL（Delay Lock Loop）和FLL（Frequency Lock Loop）的矢量设计或者利用INS信息与导航信息进行深层次的融合，可利用多个环路整体的性能优势提高单个通道的跟踪处理能力[8-10]，这类文献大都采用非线性滤波方法，如粒子滤波、扩展Kalman滤波等，但对如何定量分析矢量跟踪带来的性能分析值得更深层次的研究。矢量环虽然能在整体上提高信号跟踪的鲁棒性，但由于处理复杂度较高，因此应用得不是太多。因此，降低矢量跟踪的计算复杂度也是重点研究的问题。

在分析信号跟踪原理和建立广义环路传输模型的基础上，提出一个实用化的矢量跟踪环应用方案，即多通道数据源联合控制NCO的环路方法，利用多数据互补优势提高系统的整体性能。该结构对定位域和信号域进行有机的融合，利用最小二乘算法得到的定位域结果反向驱动控制信号环路的NCO装置，取得较好的跟踪效果。同时利用信息和噪声的定量关系说明信号跟踪和融合过程中的信息变化情况，并进行相关的试验验证。

1 信号跟踪与测量

1.1 信号跟踪的基本原理

GNSS接收机中码环和载波环的跟踪原理大致相仿，都是本地产生相位或频率一致的载波或码与接收信号混频，从而完成信号的解调和解扩。为方便起见，本文重点以DLL为例进行相关分析。接收机复制的本地码与接收码作相关运算后，相位鉴别器会估算出两者间的差异，这种相位差异用来驱动NCO产生下一个时刻的本地码，这就是标准的单路跟踪原理。

在信号跟踪的同时，采用锁存器记录伪码的相位再加上鉴别器得到的码相位差异，就可得码相位的测量值，它直接决定伪距测量的精度。从中可发现，NCO的输入输出控制是环路的核心，它的输出准确度直接决定环路跟踪的性能。

1.2 测量值的产生过程

环路在稳定跟踪的过程中会产生很重要的观测量：即码相位和载波相位。码相位是利用扩频码良好的相关性得到的，它是接收机进行伪距测量的基础。伪距的具体表达式为

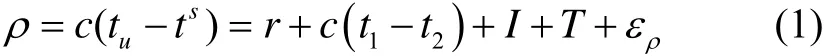
式中：tu为用户机接收时刻，ts为信号发射时刻；后式为误差展开式，r为卫星与用户间的实际几何距离，t1为用户机钟差，t2卫星钟差，I代表电离层延迟，T代表对流层延迟，ερ为卫星位置误差、大气延时估计误差、多路径误差、接收机噪声多种误差的总和。tu可由用户机时钟显示中直接读出，ts则通过测量伪码相位获得，伪距则是在此基础上的组装值。式(1)经一阶泰勒展开后可演变为

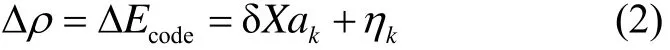
式中，Ecode为码相位，下标k为卫星编号，ak为归一化的视线方向矢量，δX为位置误差和用户机时钟偏差，kη为其他各类误差的总称。

式(2)深刻揭示码相位、伪距、位置坐标三者之间的关系。伪距定位的过程是根据用户机到各个卫星的距离变化量来推导用户的运动矢量。利用伪距量能够定位的特性，可得到伪距误差与定位误差的关系。以伪距作为桥梁，推导相位误差与距离误差的关系。这就为定位域结果反向设置信号域参数奠定理论基础。

2 跟踪环路的传输模型

2.1 模型的建立

信号跟踪的主要目的是调整本地振荡器的频率或相位使之与输入信号频率或相位相匹配，可建立系统传输函数进行理论分析。其原理[11]可抽象为如图1所示的结构框图，传递函数为

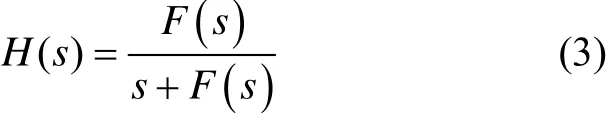
式中，F(s)为环路滤波器函数。

引入速度辅助信息后的广义传递函数为

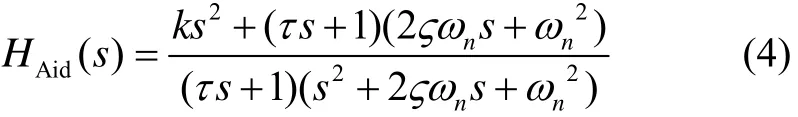
式中，k为辅助误差因子。

图1 广义跟踪环路结构框图Fig.1 Structure frame of the comprehensive tracking loop

2.2 模型影响要素的分析

造成环路跟踪误差的主要原因是输入相位噪声和速度辅助误差，利用式(3)的传输函数表达式和输入信号相位噪声密度函数可得到如下输入相位误差表示式：

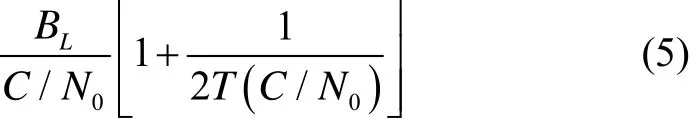
由式(5)可知，输入相位噪声与环路的带宽BL、信号的载噪比C/N0以及处理积分时间T有关联。同理可得速度辅助误差的大小与误差因子k有关联。工程应用时，速度辅助误差与INS器件的精度性能有关联。具体来说，主要受到加速度计和陀螺的偏差的影响[12]。

因此提高环路环路跟踪精度的办法也就有提高辅助速度精度和降低输入噪声这两类。速度辅助从本质上说通过抵消载体的动态来获得较小的环路噪声带宽，从而增强环路抑制外来噪声的能力。而引言中提到的矢量跟踪方法归根结底是也是通过降低噪声来提高跟踪测量的准确性，两者运用的手段有所差异。

3 基于最小二乘算法的NCO控制方法

文中第1章分析伪距测量的基本原理，建立了定位域和信号域的物理联系桥梁。第2章通过环路传输模型的理论分析指出减小环路跟踪误差的技术途径。在上述两章的基础上，本文第3章提出一个实用的利用定位域融合结果提高信号域跟踪测量精度的解决办法。采用的数学工具是最小二乘算法，主要基于以下几点理由：

① 最小二乘算法具有广泛的实用性，目前世界上绝大部分普通导航型接收机在定位解算过程中均采用最小二乘算法。该算法简单灵活，便于今后的技术推广。

② 与最小二乘相比，Kalman滤波是另一个可供选择的重要工具。但Kalman滤波涉及到向量维数多，计算复杂度较高，另外关于过程噪声以及观测噪声的参数设置对滤波结果有很大影响，显得实用性不够。

③ 从数学本质上来说，Kalman滤波在某些特定场景下的实现效果优于最小二乘算法，主要是因为其动态滤波的优越性决定的，这对减小跟踪系统的最终稳态误差并没有多大帮助。最小二乘经过分步改造同样可以利用动态调节环路噪声带宽的方法提高跟踪的精度。

3.1 结构框架

传统的标量接收机对接收到的信号进行捕获、跟踪、导航运算等步骤后会得到最终的导航结果，各通道之间相互独立，没有形成一个良好的反馈和补充机制。矢量化的接收机主导思想是将跟踪和导航运算融合在一起，利用多源信息量多的优势，形成一个数学意义上的最优解，以最大程度挖掘接收机的内部潜能。

如图2所示，为提高NCO输出的准确性，可改变单一环路的内环控制方式，即断开相位鉴别器的内输出，直接作外数据源进行引出，以此类推。多个通道的伪距数据经过预判断、联合处理以及视线方向投影变换后，得到相位更新值，从而形成更优化的NCO输出控制，提高跟踪的精度和稳定性。

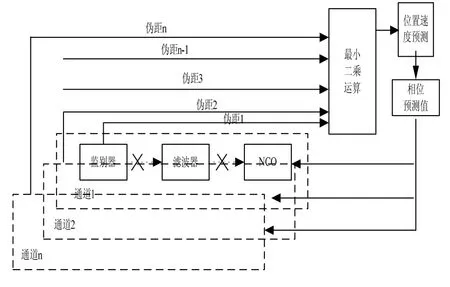
图2 多通道联合控制的NCO结构框图Fig.2 NCO structure frame driven by the multichannel

相位鉴别的算法种类很多。图2中的相位鉴别器采用了非相干超前减滞后幅值法，它是目前较流行和实用的码相位鉴别方法，计算公式为

式中，E和L分别为超前码和滞后码相关累加结果的均方根。多源NCO控制结构主要把NCO的单环模式改变成多环路联合控制模式，其他实现环节如本地码的产生、相关累加的形式与标量接收机完全相同。

3.2 算法实现中的关键技术

① 加权最小二乘

在本文中，加权最小二乘的作用是求解当前时刻接收机的位置变化值，用来反馈预测下一时刻的相位估计值。含有接收机位移信息的非线性函数可用式(7)表示：

经泰勒线性展开后得到：

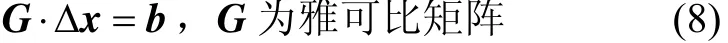
考虑到不同信道的输出值有不同的测量误差，彼此互相独立，增加不同的权重系数矩阵后，式(8)变为

求最小二乘解得到：

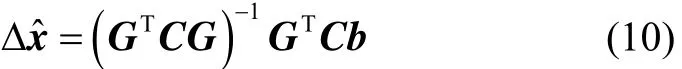
式中，C=WTW，W为权重矩阵。

不同通道之间的信号接收条件差异性很大，造成测量误差各不相同，引入权重矩阵后，可提高最小二乘计算结果的输出精度。权重矩阵元素的系数设置可由鉴相器的输出结果决定。以3.1节采用的码环工作状态为例，通常会产生超前、滞后、即时等6个状态的相关运算结果。当环路进入稳态跟踪后，利用码自相关函数主峰的对称性，能量输出应该都集中到准路，而超前和滞后两路的能量应该相等，此时运用公式(6)，对应的鉴相器输出为零。反之，超前和滞后两路的能量不相等，此时鉴相器输出的差异值越大，表明该通道越不可靠，可能处在失锁崩溃的边缘，此时应设置较小的权重矩阵系数。

② 相位预测方法

已知最小二乘算法得到的位置偏差，利用第1章的信号跟踪与测量原理，可将位置偏差在视线方向上进行投影，从而得到码相位误差。同理，速度误差也可以在视线方向上进行投影，从而得到载波频率误差，并以此驱动NCO完成本地的伪码和频率复制，完成后续的相关运算。视线方向的转换计算式如下：

式中，rk为接收机至k颗卫星的距离，x、y、z为方向分量。

3.3 性能初步分析

与单环控制NCO的方法相比，使用最小二乘联合多通道数据源控制NCO的方法可借助多通道间的互补优势提高弱信号通道的信号跟踪能力。这一现象可利用最小二乘解的误差方差理论进行解释。根据中心极限定理的理论，当试验的样本足够多时，最小二乘估计误差总体上服从渐近正态估计，表达式为

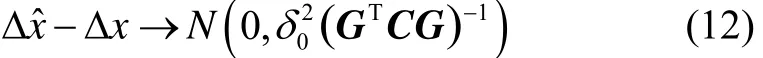
通过此最小二乘解可转化为通道伪距测量协方差矩阵：

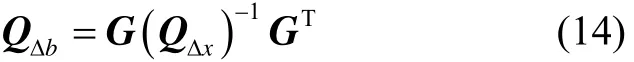
分析式(14)的特征可知， 经过多通道信息融合后，各通道的观测精度不仅与本通道的观测精度有关，（即协方差矩阵的对角线元素），而且与其他通道的观测精度有关。影响多通道反馈测量精度的因素有可见卫星的数目、各通道的观测质量、卫星的几何分布形状。通常情况下，可见卫星的数目一般在10颗以上。为便于直观理解，假设各通道的信号接收条件均相同，不考虑卫星几何分布对观测值的影响，此时经过通道融合后的测量值为所有通道测量的均值。由于最小二乘解中含有三维坐标和钟差等4个未知参数，测量值的误差方差减小为0.4。由此可见，处理的卫星信号数目越多，其信息冗余也就越多，此时误差方差越小，反馈控制NCO的精度也就越高。这就体现出联合处理的优势。测量误差的减小，意味着该通道信号接收条件的改善，即载噪比的提高，依据第2章的传输模型误差原理，可从理论上分析精确分析误差的改善程度。

4 试验综合验证

选用基于Matlab的软件接收机平台，输入的数据源为模拟信号发生器产生的中频信号，数据来源于真实场景下的跑车数据回放，动态时速在30～50 km/h。接收机具备捕获、跟踪、位同步、帧同步、定位解算等基本功能，试验过程中涉及到的各类参数可进行灵活配置，体现出软件接收机应用灵活、便于教学研究的特点。真实设备中，接收机的时钟噪声在长期范围内服从Allan方差分布，不同精度等级的晶振对应不同的相位噪声等级。在本文的仿真试验中，为简化模型的复杂度，在一个较短的处理时间间隔（ms级）内，时钟误差可近似为离散化的高斯白噪声模型。

4.1 仿真试验1

信号条件良好，可用卫星的个数为10颗，GDOP和HDOP的数值小于2，仿真时间为200 s。初始时，卫星信号的载噪比都是50 dB-Hz，PRN5号卫星信号的载噪比以0.25 dB/s的速度逐渐下降，但噪声功率始终保持不变，其余卫星信号功率维持不变。传统标量环路采用DLL+FLL的形式，采用应用最广泛的参数设置为：FLL：环路带宽15 Hz，阻尼系数0.785；DLL：环路带宽1 Hz，相关器码片间距为0.5码片，阻尼系数0.7；码相位鉴别器采用非相干超前减滞后功率法，积分时间为1 ms。图3和4分别表示了采用传统环路和本文算法的PRN5信号码相位估计误差。由图3可知，PRN5大概在95 s处失锁，而图4的PRN5大约在120 s处失锁。计算95 s和120 s时对应的载噪比差值,可推算出在该场景下利用强信号辅助弱信号的跟踪大约能增加6.25 dB的处理增益。

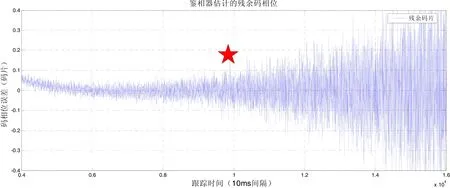
图3 传统环路估计的PRN5码相位误差Fig.3 PRN5 code phase error estimated by the conventional loop

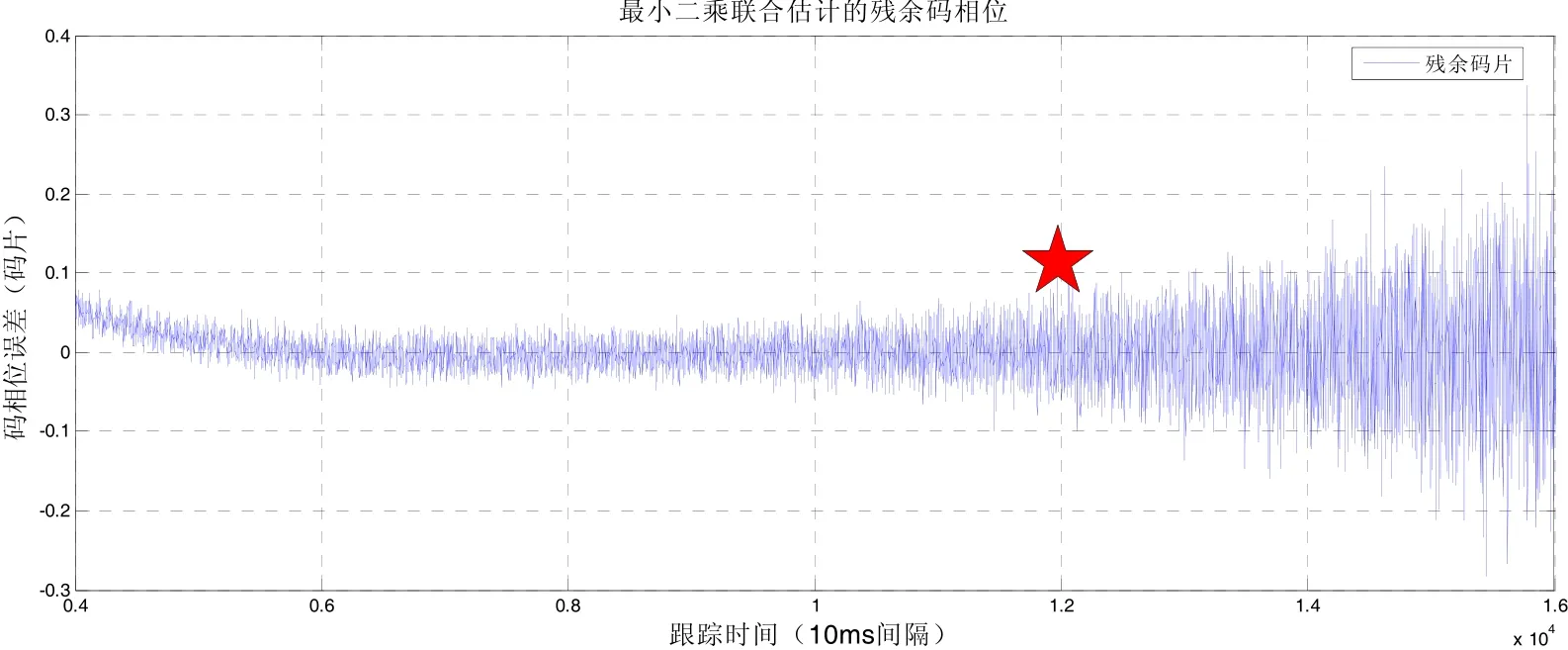
图4 多通道联合估计的PRN5码相位误差（一）Fig.4 PRN5 code phase error estimated by the multichannel (I)

4.2 仿真试验2

卫星星座布局和环路参数设置同4.1节。所有卫星信号从最初的50 dB-Hz均按照0.25 dB/s的速度逐渐下降，噪声功率保持不变，同样观测利用最小二乘联合法获得的PRN5信号码相位估计误差，具体结果如图5所示，大约在107 s处失锁，相比图3算法，约有3.25 dB的处理增益。

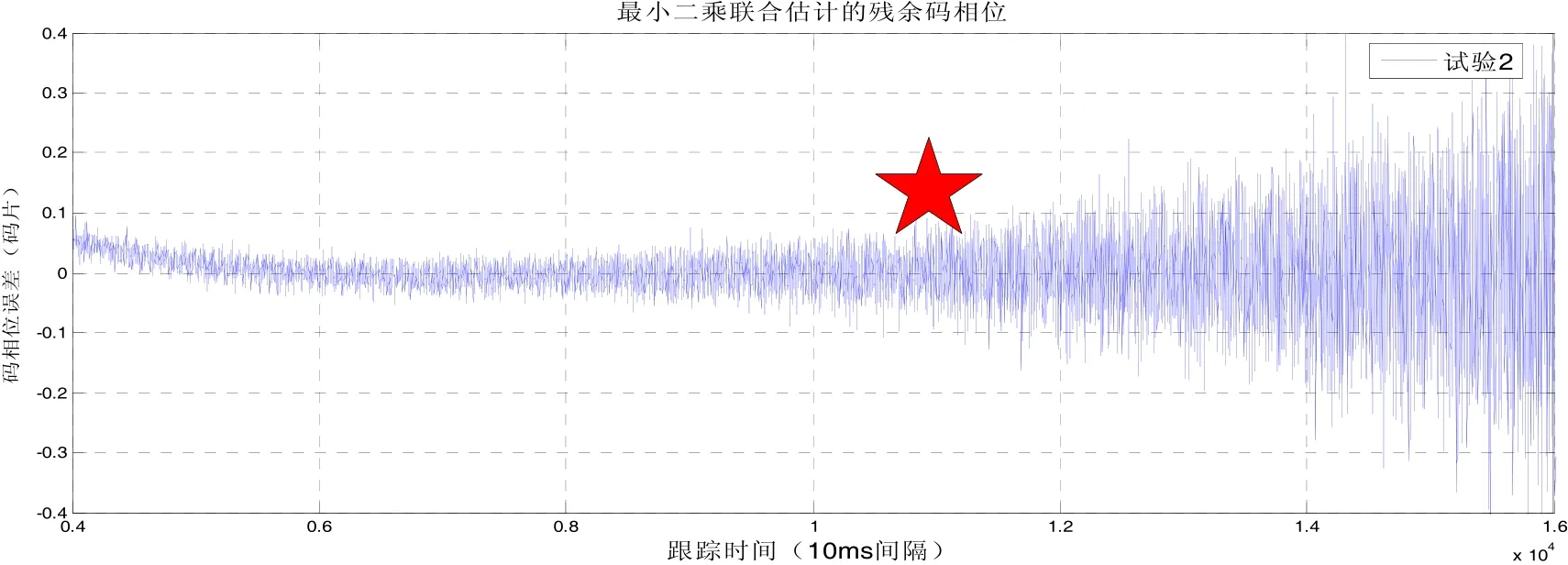
图5 多通道联合估计的PRN5码相位误差（二）Fig.5 PRN5 code phase error estimated by the multichannel (II)

4.3 仿真试验3

在某些恶劣场景下，接收机受到外界地形或者突发因素的干扰，可见卫星的数目会有所减少。采用采集回放设备事先录入真实场景下的GNSS中频信号数据，可见卫星的数目为7颗，其中两颗卫星的信号比较微弱，低于门限值3 dB左右，不能被普通接收机正常解调，其余5颗卫星信号强度正常。图6和图7分别反映了本文算法和普通接收机解算的定位精度。综合对比可知，由于本文算法低载噪比的恶劣条件下参与定位的卫星数目多，误差因子小，因此在E、N、U等各个方向都取得较好的定位效果。

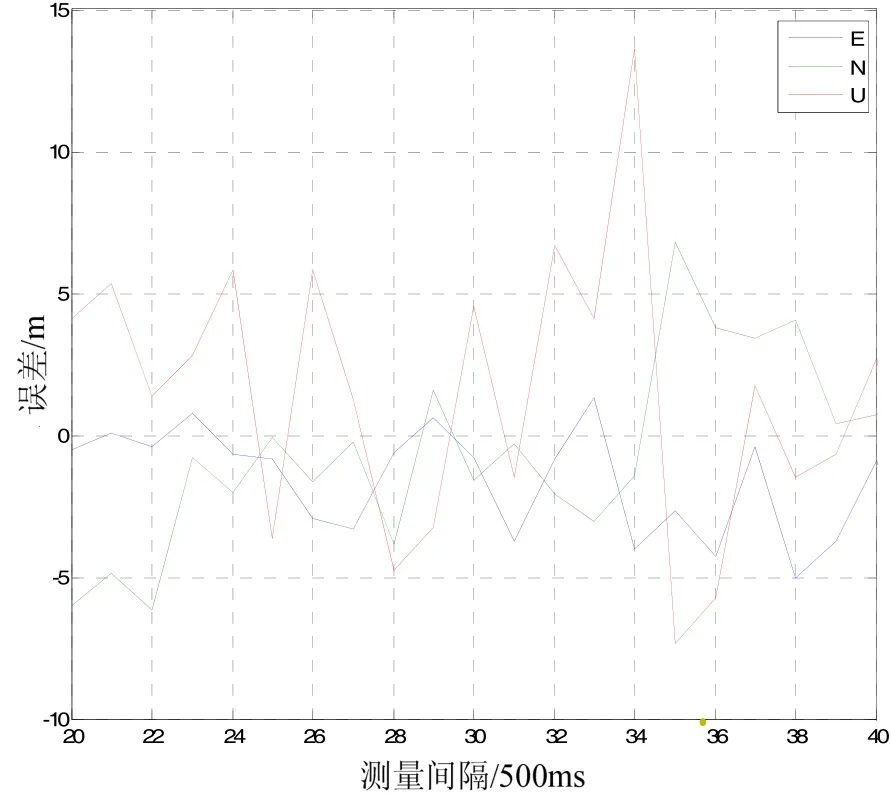
图6 多通道联合控制下的定位精度Fig.6 Position error controlled by the multi-channel

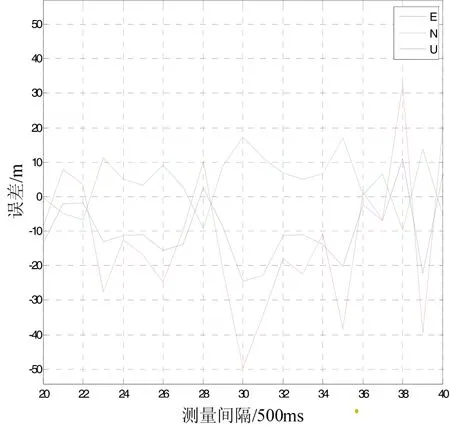
图7 普通接收机的定位精度Fig.7 Position error controlled by the conventional receiver

5 结 论

普通接收机由于采用相互独立的通道处理技术，信息未得到充分的融合，处理弱信号的能力非常有限。本文通过建立信号环路跟踪的传输模型，指出提高Doppler辅助和减小噪声方差是提高跟踪门限的重要技术途径。利用伪距定位和加权最小二乘的基本原理，设计出定位域结果反馈驱动跟踪环路的多通道联合控制NCO的算法。该算法充分利用通道间信号相互融合的优势，从整体上提高了信号的跟踪能力，增强了接收机在恶劣环境下的可用性。后续可用Doppler辅助减小信号搜索的动态不确定度，进一步提高信号的跟踪处理能力。

（References）：

[1] Jovancevic A, Brown A, Ganguly S, et al. Real-time dual frequency software receiver[C]//ION GPS/GNSS 2003. Portland, 2003: 2572-2583.

[2] Nesreen I Z, James L G. Extended Kalman filter-based tracking of weak GPS Signals under high dynamic conditions[C]//ION GNSS 2004. Long Beach, 2004: 20-31.

[3] Psiaki M. L. Smoother-based GPS signal tracking in a software receiver[C]//ION GPS 2001. Lake City, 2001: 2900-2913.

[4] Zhou Z B, Yang L, Li Y. An adaptive dual Kalman filtering algorithm for locata/GPS/INS integrated navigation [C]//China Satellite Navigation Conference. 2013: 527-541.

[5] Ahmed M. Context aware high dynamics GNSS-INS for interference mitigation[D]. Calgary University, 2011.

[6] Lv P, Lu M Q, Yao Z. Dual-update rate INS aided carrier phase lock loop for new generation global navigation satellite signals[C]//China Satellite Navigation Conference. 2013: 715-724.

[7] Ren T T, Mark G P. A standalone approach for ultratightly coupled high sensitivity GNSS receiver[C]// Session B5, ITM 2014. San Diego, 2014: 1-14.

[8] Hua L, Zhang Y, Li H, et al. A new kind of particle filter algorithm based on immune particle swarm optimization in objective tacking[J]. ICIC Express Letters, 2013, 7(1): 41-46.

[9] 张玉. 高动态下GPS矢量接收机跟踪算法与实现研究. [D]. 浙江大学, 2013.

[10] Lashley M, Bevly M D, Hung Y J. Performance analysis of vector tracking algorithms for weak GPS signals in high dynamics[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(4): 661-673.

[11] 吕鹏, 陆明泉, 冯振明. SINS/GPS紧耦合接收机载波跟踪环路分析[C]//中国第二届卫星导航年会. 2011: 1443-1446.

[12] Jiang C, Wu H, Jiao W, et al. Navigation technology research on GNSS loop structure aided by acoustic MEMS IMU[C]//China Satellite Navigation Conference. 2013: 739-749.

[13] 唐康华, 武成锋, 杜亮, 等. 高动态GNSS接收机载波跟踪环自适应最优带宽设计与试验[J]. 中国惯性技术学报, 2014, 22(4): 498-503. Tang Kang-hua, Wu Cheng-feng, Du Liang, et al. Experimental study and design on high dynamic GNSS receiver using adaptive optimal bandwidth for carrier tracking loop[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 498-503.

Loop design of numerically controlled oscillator driven by multichannel united data

WANG Qian1,2, HU Cai-bo2
(1. School of Instrumentation Science and Photo-electronics Engineering, Beihang University, Beijing 100191, China; 2. Beijing Satellite Navigation Center, Beijing 100094, China)

Signal tracking is the main processing technology of GNSS (Global Navigation Satellite System) receiver. Improving the receiver’s tracking ability could make up the inherent weakness of GNSS’s being liable to the jamming and shield. Based on the principle of signal tracking and measuring, the connection bridge between position and signal field is built by evaluating the measurement errors. The technique solutions of boosting the loop performance are concluded by analyzing the abstract loop transmission model. The classical design idea that the channels are mutual independent are changed, and the vector loop tracking algorithm is proposed based on the NCO (Numerically Controlled Oscillator) controlled by multichannel data in the weighted least square algorithm. The new method is analyzed by theory and simulation tests. The test results show that this method can improve the processing ability of faint signal, the tracking sensitivity is increased by more than 3 dB compared with the common receiver with the same complexity, and the gain is increased by 6 dB when the channel of weak signal is assisted by the other channels of strong signals.

GNSS; numerically controlled oscillator; least square algorithm; signal tracking

U666.1

A

1005-6734(2015)04-0483-06

10.13695/j.cnki.12-1222/o3.2015.04.012

2015-02-26；

2015-07-22

国家自然科学基金项目（41474027）

王前（1978—），男，博士，从事组合导航研究。E-mail：wqaloha@139.com