柴油机实车缸套磨损快速计算模型设计
杨绍卿, 王宪成, 赵文柱
(装甲兵工程学院机械工程系, 北京 100072)
柴油机实车缸套磨损快速计算模型设计
杨绍卿, 王宪成, 赵文柱
(装甲兵工程学院机械工程系, 北京 100072)
针对重型车辆柴油机缸套磨损在实际使用过程中检测难度大、测量过程复杂的问题,基于柴油机缸套磨损的仿真计算,依据Archard黏着磨损模型、二体磨粒磨损模型以及表面粗糙度变化规律,设计了一种适用于实车不拆解检测的缸套磨损快速计算模型,并进行了实车验证。结果表明:表面粗糙度计算误差为7.1%,缸套磨损深度计算误差为10.4%,模型误差较为合理,可以应用于实车计算。
缸套磨损;柴油机;快速计算模型
目前,重型车辆柴油机使用时普遍采用摩托小时数或里程数来评估缸套的磨损,评估误差很大;同时,对于实车很难做到不拆解检测,且存在检测难度较大、过程复杂的问题,这在一定程度上增加了车辆维护保养的难度[1]。传统上监测变工况柴油机缸套的磨损情况时,需要经过柴油机工作过程数值计算、传热过程计算、润滑计算、动力学计算及磨损系数和表面粗糙度预测等一系列复杂的运算,所使用的大型计算软件较多,无论是在耗时上还是在复杂程度上都难以适用于实车。本文基于一系列简化和假设,依据Archard黏着磨损模型、二体磨粒磨损模型以及粗糙度变化规律,通过平稳载荷磨损实验、动载荷磨损实验以及模拟计算,尝试建立一种适用于实车的、高效的简化缸套磨损快速计算模型,为指导和改进柴油机实车使用提供依据。
1 磨损模型分析
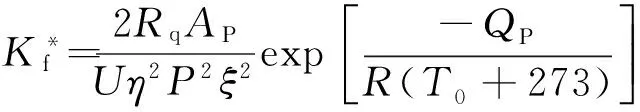
(1)
式中:U为滑动速度;Rq为表面粗糙度;P为载荷;R为摩擦表面轮廓粗糙度;T0为表面温度;ξ为油膜厚度;AP、η、QP为与材料性质和润滑状态有关的参数。
1.1 Archard黏着磨损模型
在Archard黏着磨损模型中,其基本假设为摩擦副表面半球状微凸体沿着球面发生黏着破坏,如图1所示。
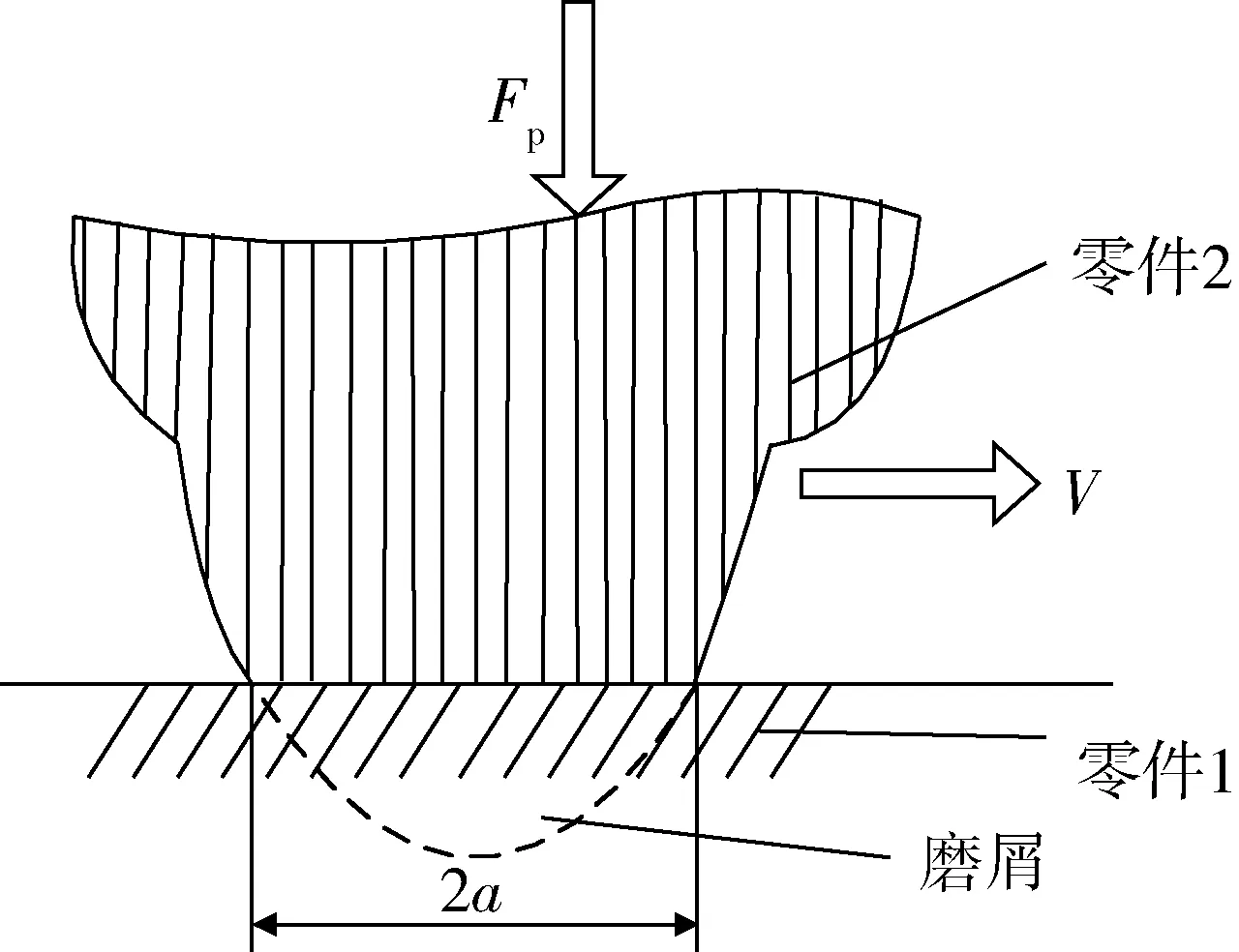
图1 Archard黏着磨损模型原理
依据Archard黏着磨损模型的基本假设可知:零件1比零件2表面硬度小,磨损几乎全部发生在零件1上;在零件表面微凸体接触压力Fp的作用下,接触点发生塑性变形,形成直径为2a的半球,且在滑动2a距离后产生磨屑,磨屑的体积即为半球体的体积。当发生塑性变形后,微凸体的接触面积δA和磨屑体积δV分别为
δA=πa2=δFp/Hd,
(2)
δV=2πa3/3,
(3)
式中:Hd为材料表面硬度。
由图1可知:磨损的滑动行程L=2a。可计算得到整个滑动面的磨损量M为
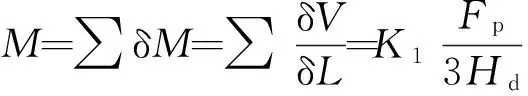
(4)
式中:K1为比例常数,即一对微凸体一次滑动过程产生一个磨损颗粒的概率。
对常数进行化简,令K1/3=Ka,可以得到磨损体积V的表达式为
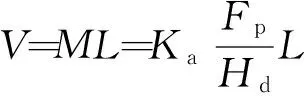
(5)
式中:Ka为黏着磨损系数。
1.2 二体磨粒磨损模型
在缸套磨损中,磨粒的犁沟作用常常使摩擦副表面出现剪切、犁皱和切削,导致缸套表面出现磨痕[5]。因此,在选择磨损模型时,需要考虑磨粒磨损。磨粒磨损模型原理如图2所示。
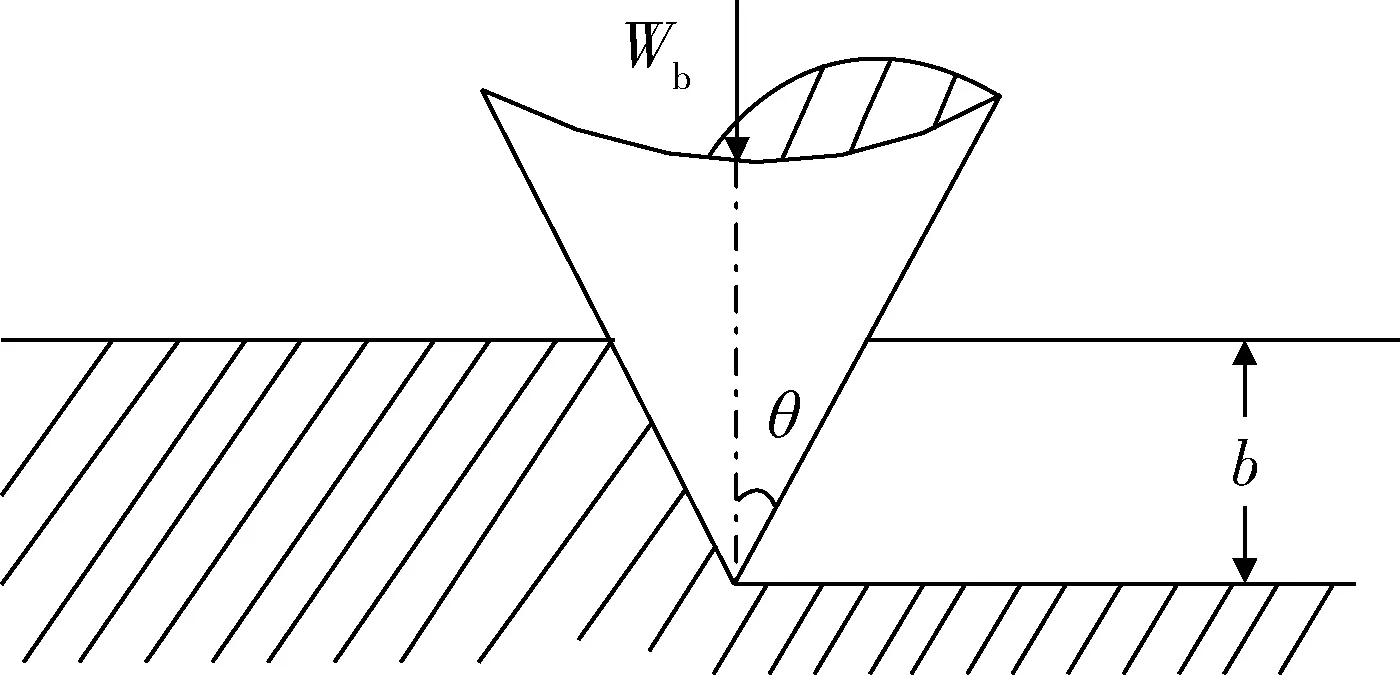
图2 磨粒磨损模型原理
忽略磨粒分布情况、材料弹性变形以及接触面积变化等因素的影响,仅考虑圆锥状磨粒。设压入表面材料部分投影面积Ab为
Ab=πb2tan2θ,
(6)
式中:b为压入深度;θ为锥体半角。可以得到每个磨粒所承受的载荷Wb为
Wb=σsAb=σsπb2tan2θ,
(7)
式中:σs为被磨材料的受压屈服极限。
当磨粒滑动距离为L时,表面材料被磨去体积V1和磨损体积V的表达式分别为
V1=Lb2tanθ,
(8)
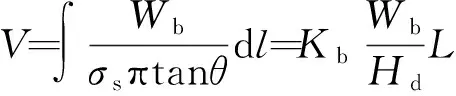
(9)
2 磨损模型综合修正
2.1 粗糙度计算表达式推导
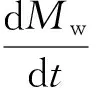
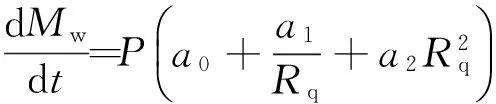
(10)
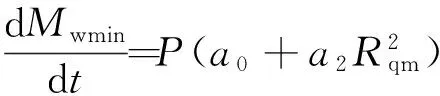
(11)
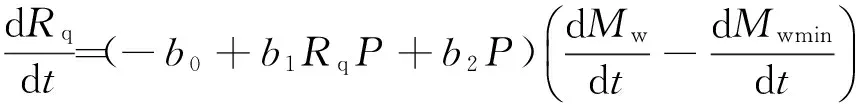
(12)
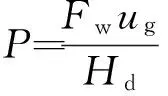
当Mwmin=0时,将式(11)代入式(12),可得
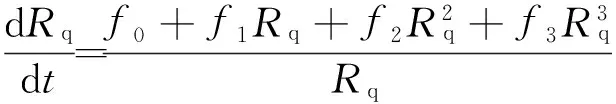
(13)
式中:fk(k=0, 1, 2, 3)为由工况确定的参数。
由式(13)可以发现: 当忽略接触表面的最小磨损量时,在磨合的过程中,Rq是一个自变量为t的指数函数,可将其改写为
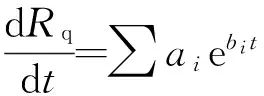
(14)
对于缸套-活塞环摩擦副,前苏联科学院机械研究所[7]的研究表明:对于某一个确定的工况,摩擦副的表面粗糙度存在一平衡值,即平衡粗糙度,使得在该工况下摩擦副表面磨损率最小;同时,磨损系数的大小与表面粗糙度近似成二次曲线关系。
2.2 表面粗糙度变化规律
图3为表面粗糙度与磨损率的关系,当表面粗糙度为该工况所对应的平衡粗糙度时,磨损率最小,该规律并不包含时间。不管初始粗糙度为何值,对某一个确定工况,经过一定时间后,其表面粗糙度最终都将收敛到其工况所对应的平衡粗糙度。
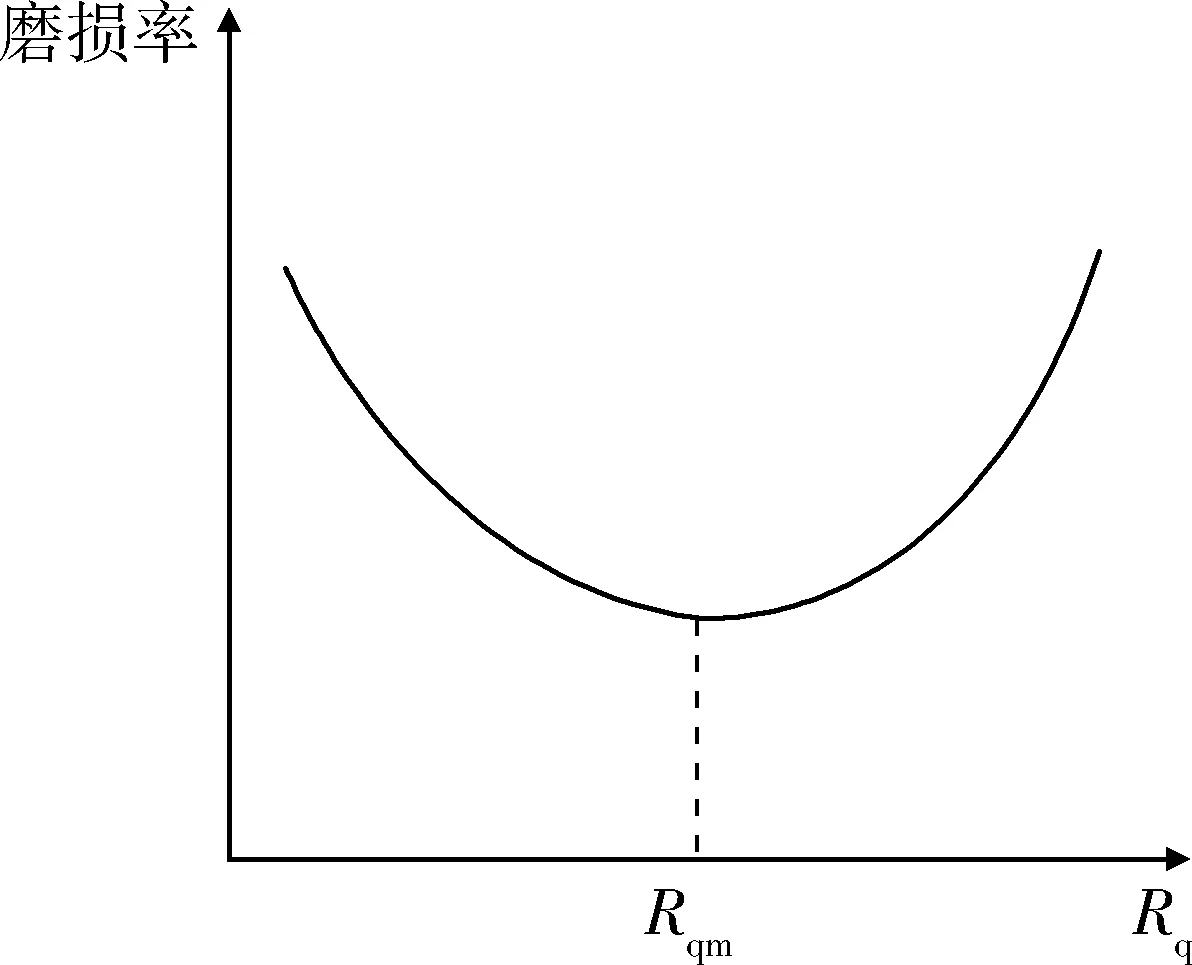
图3 表面粗糙度与磨损率的关系
由于发动机缸套-活塞环实际工作过程很复杂,为建立实车快速计算模型,需进行以下假设:
1) 忽略剧烈磨损时摩擦副表面粗糙度和磨损系数的变化;
2) 一个特定工况(速度和载荷一定)对应且只对应一个平衡粗糙度;
3) 表面粗糙度在向较大值发展时,其规律与向较小值发展时相同,前后对称;
4) 忽略磨损过程中摩擦生热和缸套散热对缸套硬度的影响,认为缸套硬度保持不变。
根据“浴盆曲线”磨合阶段粗糙度的指数函数规律[8]并结合式(14),得到Rq的表达式为
Rq=c1ec2t,
(15)
式中:c1、c2为由工况唯一确定的参数。
因Rqm只与工况有关,而与粗糙度初始值无关,由上述假设及式(15)可得到Rq与t的关系式:
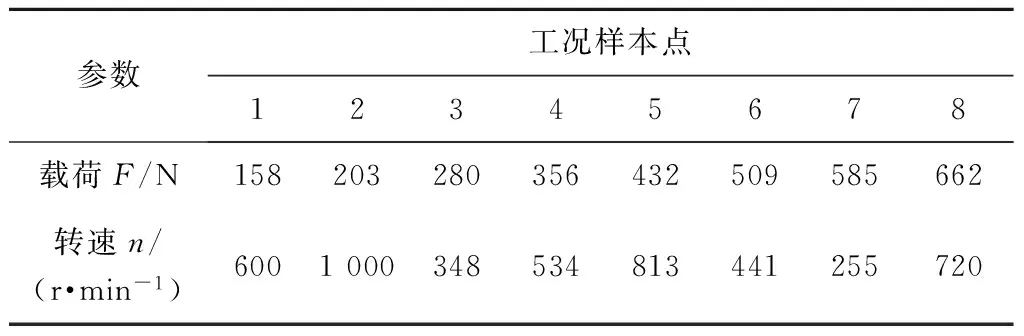
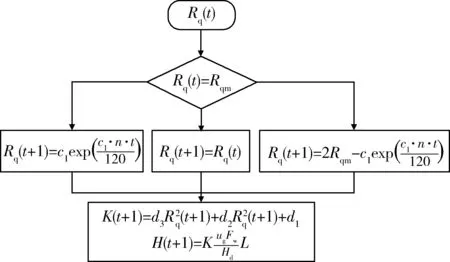
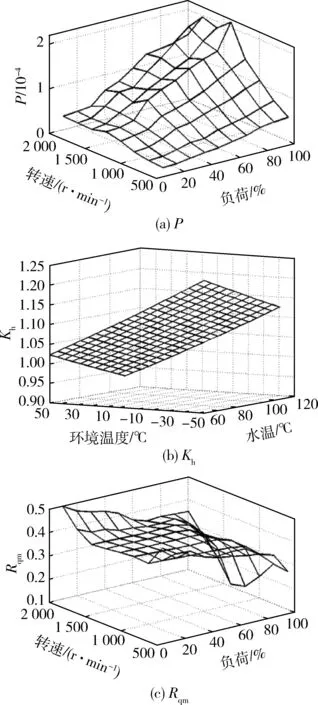
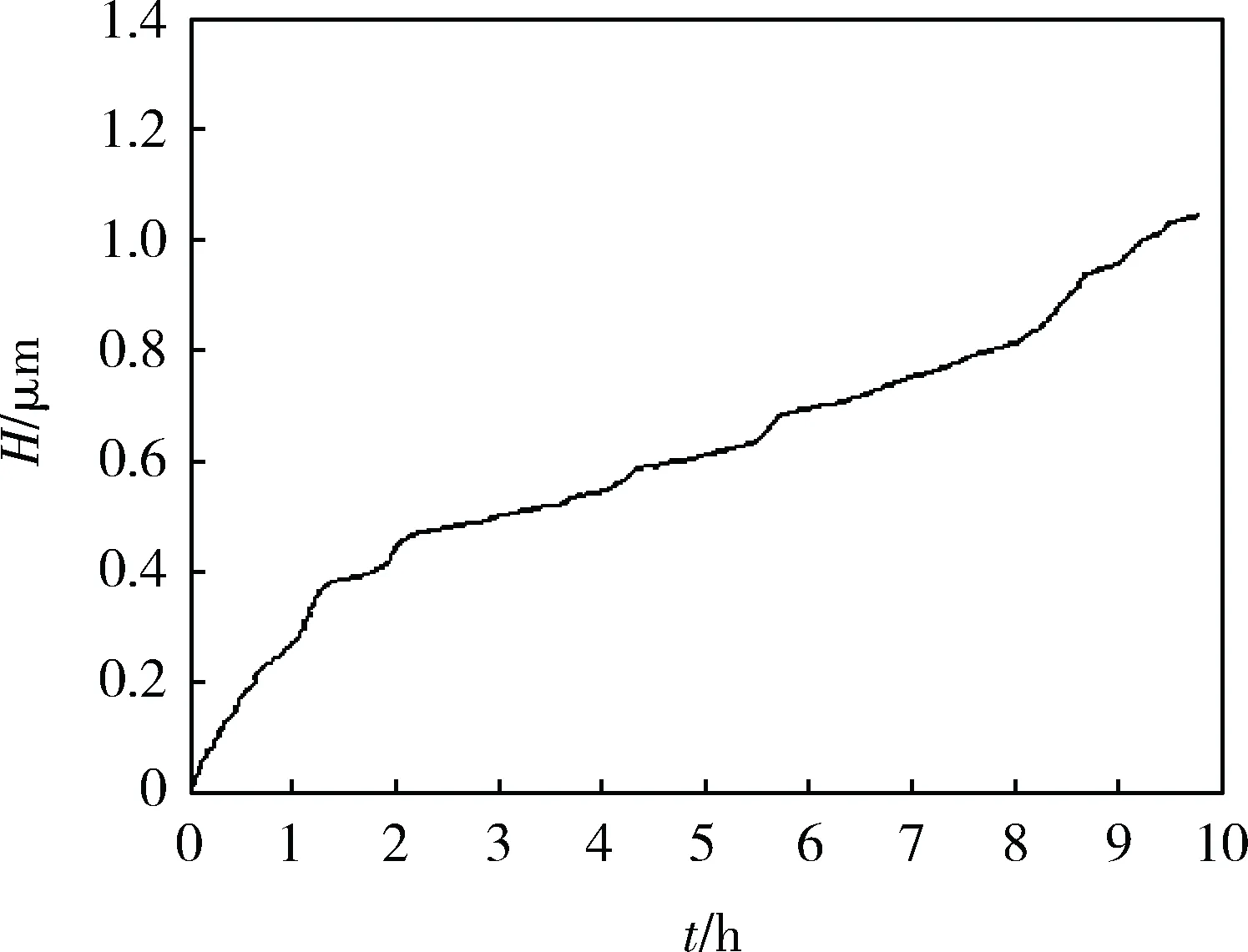
1) 当Rq Rq(t+Δt)=2Rqm-c1ec2t; (16) 2) 当Rq>Rqm时,摩擦副处于磨合阶段,有 Rq(t+Δt)=c1ec2t; (17) 3) 当Rq=Rqm时,摩擦副处于稳定磨损阶段,此时磨损量最小,有 Rq(t+Δt)=Rqm。 (18) 2.3 磨损深度求解 由磨损体积V的表达式(5)、(9)可知:2个公式在形式上统一,区别在于磨损系数K不同。借鉴上述形式,可得到摩擦副磨损量M的表达式为 (19) 磨损深度的表达式为 (20) 磨损深度随时间的变化规律为 (21) 式中:ρ为摩擦副表面材料密度;s为磨损区域的面积;Nw为由时间与柴油机转速所确定的当量转数,用于衡量摩擦副之间往复的次数。 2.4 磨损系数K求解 当工况确定时,在磨损量表达式中K与Rq近似成二次曲线关系[7],其待定系数可由实验确定。因此,可得到K的近似数学表达式为 (22) 式中:d1、d2、d3为由柴油机工况确定的系数。 3.1 磨损实验设计与测试 磨损实验的试件采用与实际缸套相同的加工工艺。活塞环上试件采用65Mn合金钢毛坯,经车床、铣床、磨床加工至基本尺寸,再经去毛刺、退磁、镀铬、高精度磨平处理后,得到Rq=1μm、Hd=900 HB的上试件;缸套下试件采用42MnCr52合金钢,毛坯加工至基本尺寸,再经感应淬火后精磨至工艺需求,得到Rq=1.5 μm、Hd=700 HB的下试件。MM10W万能磨损实验机和磨损试样如图4所示,其中:活塞环上试件为旋转件,缸套下试件为固定件,接触形式为面接触,二者的接触面积为98 mm2。 依据柴油机实际使用中燃油消耗量、转速、水温、油温等多个参数的测试结果,对柴油机缸内的热力过程进行仿真计算[9]。依据仿真计算得到的各个曲轴转角位置所对应的载荷条件,选取3 °CA处为考察点,以CD40滴油润滑方式模拟缸套磨损边界润滑条件,实验机加载转速n的范围为255~1 000 r/min,实验机F的范围为50~662 N。 图4 MM10W万能磨损实验机和磨损试样 为尽可能模拟更多工况,采用拉丁超立方方法[10]进行8个工况样本点的实验,如表1所示,其实验磨损结果如表2所示。 表1 实验工况 表2 实验磨损结果 3.2 工况参数求解 结合式(19)、(22)及仿真计算结果,可拟合得到磨损系数K与Fw、ug之间的预测关系。这里采用低阶多项式响应面方法[11]进行拟合逼近,其所需数据点数量与模型中的变量数量直接相关。其一般表达式为 (23) 式中:Xk对应式(15)、(22)中的c1、c2、d1、d2、d3;xki为第i个工况参数对应的第k个待定系数。 将表2的实验数据代入式(23),得到各系数的值,如表3所示。 表3 磨损模型计算系数 4.1 系统参数拟合 将采集到的柴油机油耗和转速数据作为输入,依据表4中8个工况点的系统参数值,采用表格函数法和RBF神经网络求解,得到系统参数对应各个工况的分布情况,如图5所示,其中:图格的节点处为各参数的计算值。 在实际计算中,为方便连续工况的计算,对各参数进行MAP插值,实现对计算值的拟合,实车计算时程序可根据对应输入工况直接查找拟合参数值,以提升计算速度。 4.2 计算过程 采用实时累计计数和的方法,计算1 s内的缸套表面粗糙度、磨损深度和磨损系数,上1 s结束时的状态是下1 s开始计算的初始状态,从而实现对变工况磨损深度的快速计算,其计算过程如图6所示。 图5 系统参数对应各个工况的分布情况 图6 变工况磨损深度计算过程 为了进一步加快计算速度,将工况所对应的载荷、硬度修正系数、平衡粗糙度进行拟合处理,如图7所示,其中:硬度修正系数Kh以海拔100 m、大气温度20 ℃、水温80 ℃时和海拔100 m、大气温度0 ℃、水温60 ℃时的缸套硬度线性拟合得到[12]。依据线性拟合结果,程序在计算时可快速查找工况所对应的平衡粗糙度和载荷参数的拟合值,进一步提升了计算速度。 图7 P、Kh、Rqm拟合处理结果 在普通越野测试场地上,将模型应用于某型装甲车辆进行实车测试。测试前,测得柴油机1#缸套3 °CA位置,Rq=0.655 μm,并记录3 °CA位置处缸套直径,设定为磨损深度的基准。场地每圈为3 km,车辆运行时间为9.8 h,计算1#缸套的磨损状况。测试完毕后,得到计算的缸套H变化情况如图8所示。 图8 缸套H变化情况 计算得到1#缸套3 °CA位置处Rq=0.287 μm,测试后对1#缸套进行拆解检测,其Rq=0.309 μm,计算误差为7.1%;计算得到1#缸套表面3 °CA位置处H=1.043 μm,实车检测结果为H=0.945 μm, 计算误差为10.4%。结果表明:该实车磨损计算模型误差较为合理,能够对实车使用中缸套的磨损进行可靠预测。 1) 依据Archard黏着磨损模型、二体磨粒磨损模型、磨损系数变化以及表面粗糙度的变化规律,基于一系列假设,推导了基于平衡粗糙度的柴油机缸套磨损深度计算公式,可应用于实车计算。 2) 建立了以转速和油耗为输入的实车快速计算模型,并通过9.8 h实车测试进行了验证。测试结果表明:计算模型对粗糙度计算误差为7.1%,对磨损深度计算误差为10.4%,模型计算误差较合理,且计算速度快,输入参数采集无需拆解,具有实车应用价值。 [1] 张稀林,贺立峰. 内燃机气缸套磨损检测与使用寿命预测[J]. 车用发动机,2008,173(1):81-84. [2] 孔凌嘉. 内燃机缸套活塞环摩擦学系统研究[D]. 西安: 西安交通大学, 1991. [3] 刘峰璧, 谢友柏. 二体磨损动态过程的数学模型[J]. 机械科学与技术,1995(增刊):21-25. [4] Halling J.Toward a Mechanical Wear Equation[J]. Journal of Tribology,1983, 105(10): 212-220. [5] 李奇, 王宪成, 何星, 等. 高功率密度柴油机缸套-活塞环摩擦副磨损失效机理[J].中国表面工程, 2012, 25(4): 36-41. [6] Hu Y Z,Li N, Tonder. A Dynamic System Model for Lubricated Sliding Wear and Running-in [J]. Journal of Tribology, 1991,113(77): 499-505. [7] 温诗铸, 黄平. 摩擦学原理[M].3版. 北京: 清华大学出版社, 2008. [8] 王艳,周仲荣.TC4合金冲击磨损性能与机制的研究[J]. 润滑与密封,2009,34(6):1-4. [9] 张晶. 基于数值仿真的装甲车辆发动机环境适应性分析与评价研究[D]. 北京:装甲兵工程学院,2010. [10] 于晗, 钟志勇, 黄杰波, 等. 采用拉丁超立方采用的电力系统概率潮流计算方法[J]. 电力系统自动化, 2009,33(21):32-35. [11] 于一发,张大庆.基于正则化方法的多元数据拟合问题[J].辽宁科技大学学报. 2013,36(4):12-14. [12] 胡小平, 黄之初, 胡燕平. 柴油机状态实时监测系统的研制[J]. 制造业自动化, 2001,23(9):57-59. (责任编辑: 尚菲菲) Design of Fast Calculation Model of Diesel Engine Cylinder Liner Wear on Vehicle YANG Shao-qing, WANG Xian-cheng, ZHAO Wen-zhu (Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China) Aiming at the problem that the wear of cylinder liners on heavy diesel engine is difficult and complex to measure, on the basis of Archard model of adhesive wear, double-body model of wear, the change rule of the surface roughness and the simulation of diesel engine cylinder liner and piston ring, an applicable fast calculation model of cylinder liner wear is designed and tested on the vehicle. The results indicate that the calculation error of the surface roughness is 7.1%, the calculation error of cylinder liner wear depth is 10.4%, the accuracy of the model is acceptable, which can be applied to a practical calculation. cylinder liner wear; diesel engine; fast calculation model 1672-1497(2015)03-0041-06 2015-01-08 军队科研计划项目 杨绍卿(1991-),男,硕士研究生。 TK421 A 10.3969/j.issn.1672-1497.2015.03.009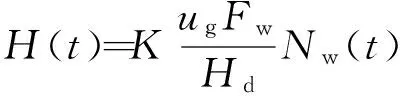
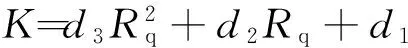
3 工况参数求解


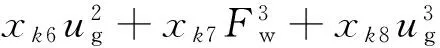

4 快速计算模型建立

5 实车验证
6 结论

