基于小波相关排列熵的齿轮故障特征提取

丛 华， 崔 超， 江鹏程， 刘远宏， 冯辅周

(1. 装甲兵工程学院科研部， 北京 100072； 2. 装甲兵工程学院机械工程系， 北京 100072)

基于小波相关排列熵的齿轮故障特征提取

丛 华1， 崔 超2， 江鹏程2， 刘远宏2， 冯辅周2

(1. 装甲兵工程学院科研部， 北京 100072； 2. 装甲兵工程学院机械工程系， 北京 100072)

针对齿轮变速箱振动信号信噪比不高、特征提取困难的问题，提出了基于小波相关排列熵的故障特征提取方法。利用具有自适应功能的小波域空间滤波器，对不同工况下的齿轮信号进行了降噪处理，运用排列熵算法计算了降噪信号的排列熵变化曲线，通过比较齿轮不同状态下的小波相关排列熵特征值来提取故障特征。在变速箱故障模拟试验台上采集了正常、磨损和断齿3种状态时的振动信号进行计算，结果表明：该方法能有效提取齿轮故障特征。

齿轮；故障特征；小波相关；排列熵

齿轮变速箱工作时的振动信号包含齿轮的周向振动、轴向振动、径向振动以及故障时引起的异常振动[1-2]。齿轮振动信号在正常状态时，其频谱主要由齿轮啮合频率及其谐波分量组成；发生故障时，由于回转频率对啮合频率及其倍频的调制，在频谱上形成了以啮合频率为中心、等间隔分布的2个边频带[3]。对齿轮振动信号进行故障特征提取是实现故障诊断的关键，目前，具有代表性的方法有基于Fourier变换的经典信号分析法、高阶频谱分析法和奇异值分解法。基于Fourier变换的信号异常检测能够在频谱上大概显示出信号中主要频率成分的变化，在给定时间间隔和频率间隔内效果比较明显，但频率分辨率较低[4]；高阶频谱分析法弥补了功率谱等二阶统计量不包含相位信息的缺陷，并且可以有效提取非高斯信号的特征，但其前提是噪声信号必须服从高斯分布，一定程度上限制了该方法在故障特征提取领域的应用[5]；奇异值分解法针对时间序列提取异常信息，运用数学原理直接进行处理，但计算复杂，且易受噪声及奇异值修正方法的影响，效率较低[6]。笔者针对齿轮信号的特点和以上故障特征提取方法的局限性，引入滤波效果较好的小波相关滤波法对原始采样信号进行降噪处理,利用对信号变化特征敏感的排列熵算法，对齿轮振动信号复杂性变化进行量度，提取隐藏在振动信号中的故障信息，最后通过试验验证该方法的有效性。

1 小波相关排列熵的基本原理

1.1 小波相关滤波

小波相关滤波法(Wavelet Transform Correlation Filter, WTCF)降噪的基本思想是基于小波分解后相邻层系数的相关性，将信号的小波变换系数在几个分解层次上进行相关运算，利用阈值检验从噪声中检出重要的信号边缘并移除噪声，从而提高信噪比。算法具体流程如下。

1) 小波分解。选择合适的小波基对原始信号进行分解，得到不同频段的小波系数。

2) 相关运算。求取各层与相邻层的相关值Cl(q,n)，得到增强的信号和变弱的噪声，即

(1)

式中:q为小波分解层数；n为时间点；l为相关运算所包含层数；W表示小波变换；N为离散信号长度。

3) 归一化处理。将Cl(q,n)归一化到W(q,n)的能量上，其归一化后的相关值为

Dl(q,n)=T·Cl(q,n),

(2)

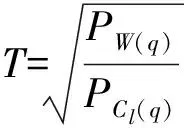
(3)

式中:PW(q)和PCl(q)分别为第q层小波系数的重构信号和相关函数的能量,且有

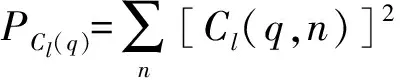
(4)

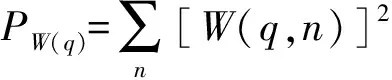
(5)

4) 阈值比较。设Sp为小波域空间滤波器，初始化时全部元素置0，Wf为滤波后的小波值。若|Dl(q,n)|≥|W(q,n)|，则将W(q,n)赋予Wf的相应位置，并将W(q,n)置0，同时将Sp相应位置置1；否则，将W(q,n)予以保留。返回步骤2)，直至PW(q)满足一个与噪声能力水平有关的给定阈值比t(q)[7]为止。

5) 信号重构。将每层原始小波系数与对应的小波域空间滤波器Sp做点乘，即可得到小波相关滤波后系数。

1.2 排列熵理论

对一时间序列{x(i),i=1,2,…,N}进行相空间重构，根据延迟嵌入定理，得到重构信号[8]：

X(i)=(x(i),x(i+τ),…,x(i+(m-1)τ))。

(6)

式中:m为嵌入维数；τ为延迟时间。

将X(i)中的元素按照升序重新排列，用j1, j2,…, jm表示重构分量中各个元素所在列的索引，即

x(i+(j1-1)τ)≤x(i+(j2-1)τ)≤…

≤x(i+(jm-1)τ),

(7)

于是，对于X(i),总可以得到一组符号序列

S(h)=(j1,j2,…,jm),

(8)

式中:h=1,2,…,k，且k≤m!，即m维相空间映射不同的符号序列(j1，j2,…, jm)总共有m!种，S(h)是其中的一种排列。计算每一种符号序列出现的概率Ph，则X(i)的排列模式熵可以按照Shannon熵的形式定义：

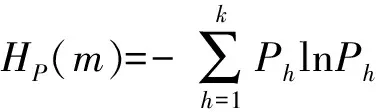
(9)

用ln(m!)将HP(m)归一化处理，定义排列熵为

HP=HP(m)/ln(m!)。

(10)

排列熵值随时间序列复杂度的增大而增大，在实际系统中，还需要考虑时间序列的长度L，在采样频率合适(满足采样定理)的情况下，L应该大于1个周期内所采集的点数[9]。通过选择合适的参数，就可以用单一的时间序列反映系统的动力学特性。

2 齿轮振动信号采集

图1为某型坦克变速箱齿轮故障模拟试验装置，主要由转速控制台、电动机、测试平台和电磁测功机等组成。电动机为三相异步电机，主要提供动力，其输出转速由变频柜调节。电动机输出轴与变速器输入轴间用联轴器连接，变速箱的主动轴通过中间轴传递给主轴，将转速输出，主轴再和一个电磁测功机相连，电磁测功机在此起到负载的作用。

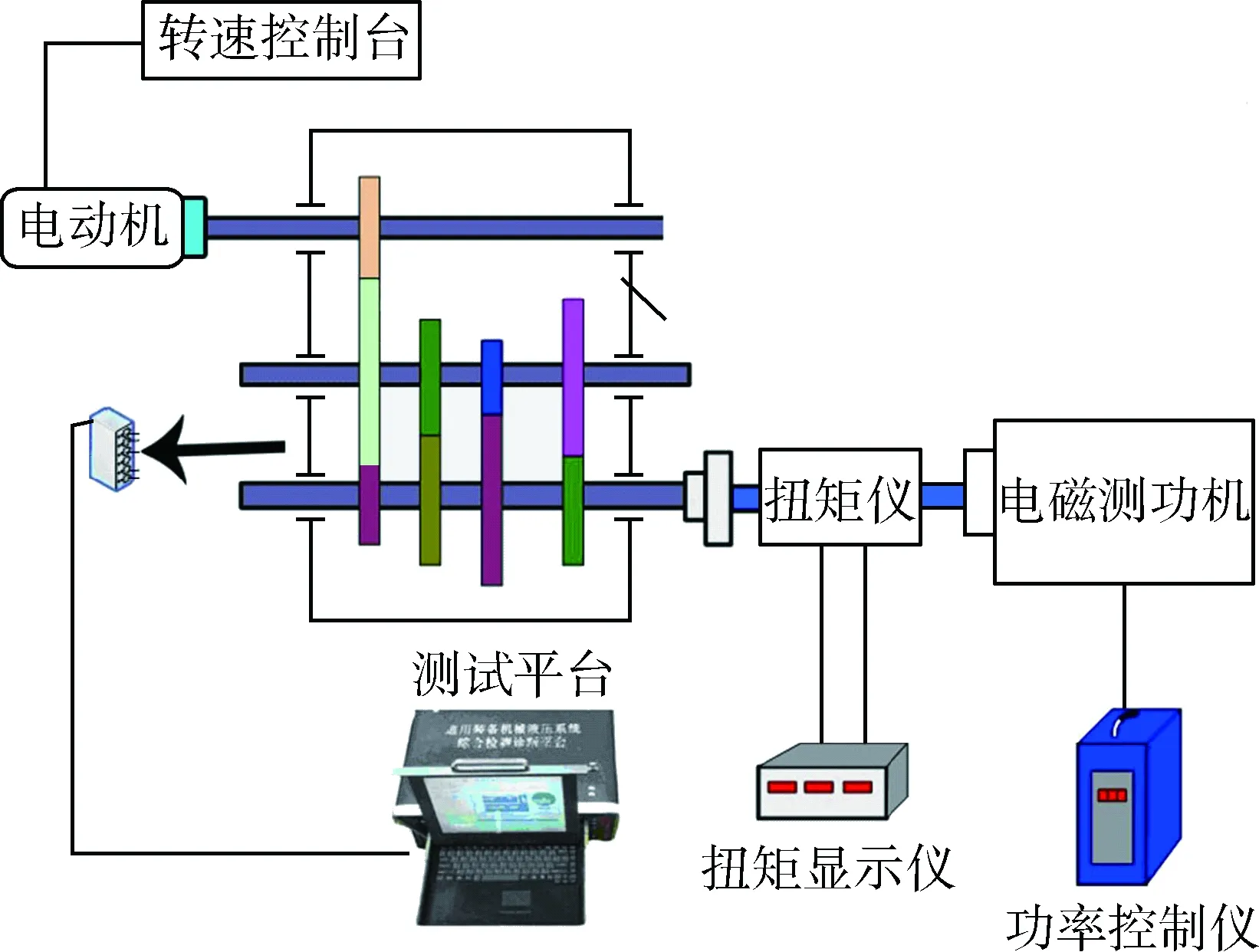
图1 变速箱齿轮故障模拟试验装置

试验中变速箱挂Ⅱ挡，设定输入转速为1 200 r/min，负载为0 N·m。传感器选用DYTRAN公司生产的3215M1型单自由度加速度传感器，采集齿轮在正常、磨损、断齿等状态下箱体的振动信号。在Ⅱ挡被动齿轮某齿面上，利用电切割在齿面上磨1～1.5 mm深度，模拟齿面磨损故障；通过电切割切掉一个齿，模拟齿轮断齿故障。上箱体测点布置如图2所示，采样频率为20 kHz，采样时间统一为5 s，每种状态采集数次，每个样本包含100 000个采样点。对比反映信号强度的评价指标，即幅值、幅值平均值以及均方根值[10]，可知测点1、3结果最优，同时这2个测点距离振源较近，能够较好地反映该挡位工作时箱体的振动情况。图3为测点3采集的样本信号前1 s的振动波形。

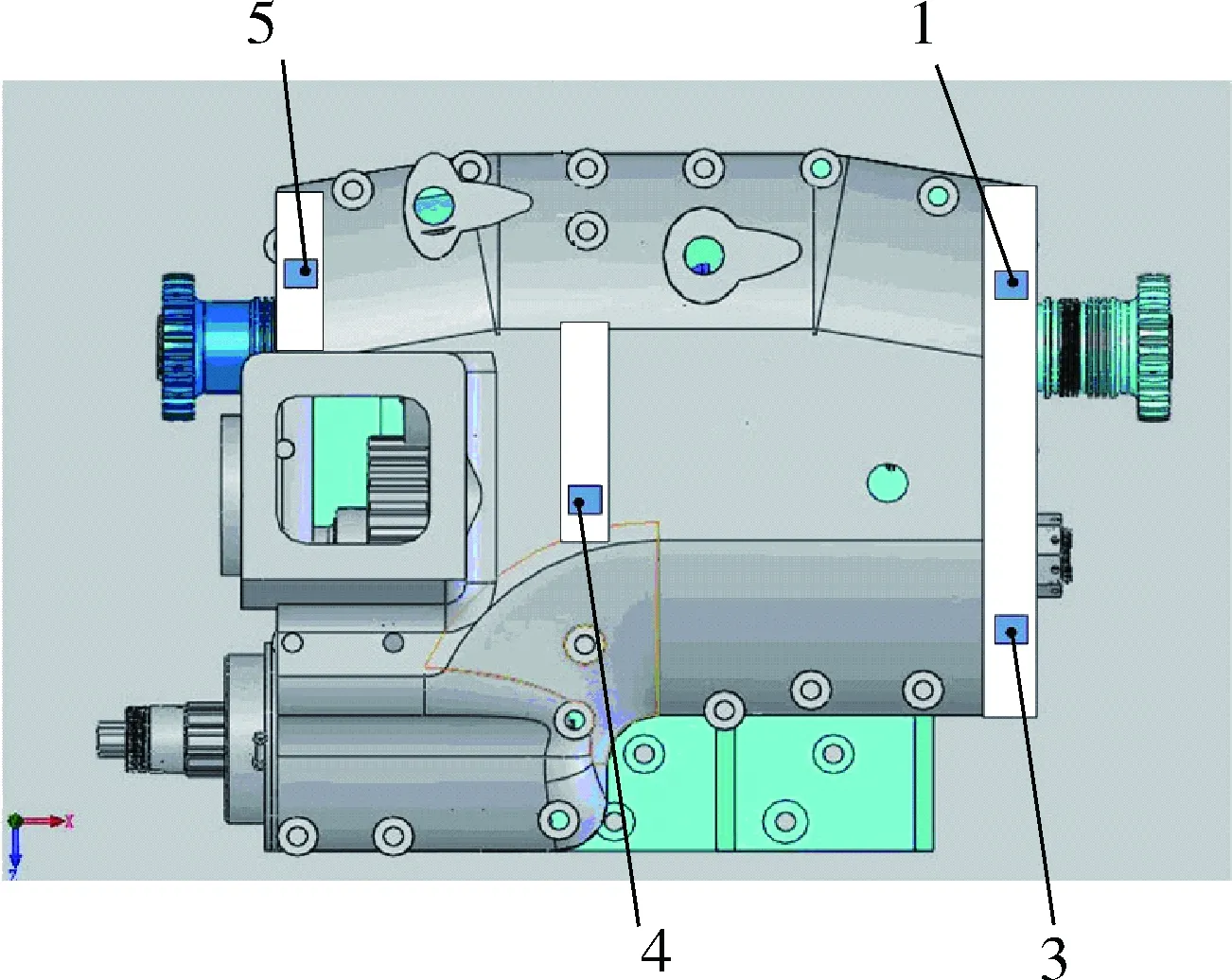
图2 上箱体测点示意位置

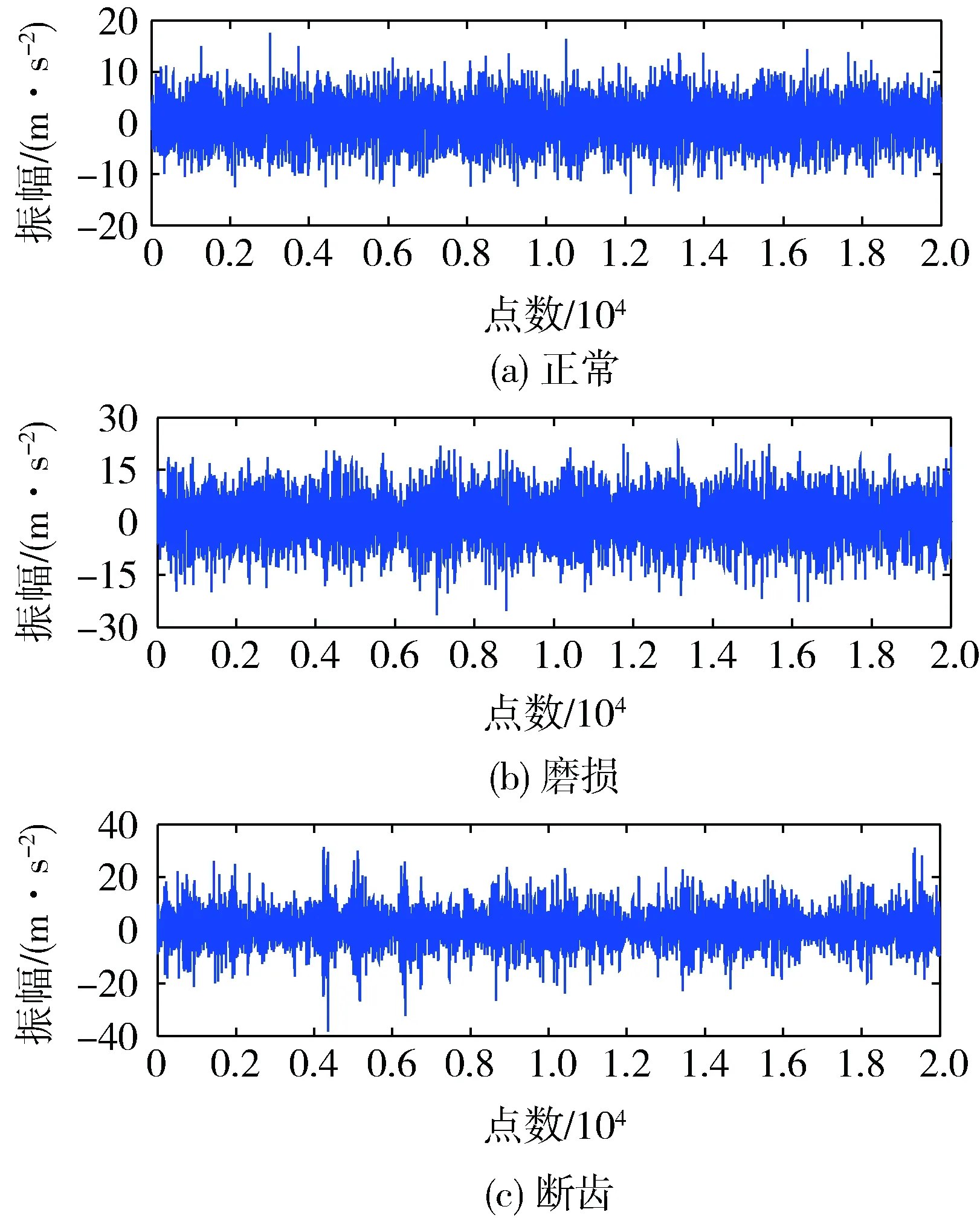
图3 测点3采集的变速箱体振动信号

变速箱正常运转时，其箱体上的振动主要是由齿轮对自身的啮合所引起的啮合振动，其振幅较为平稳，波形略成周期性，如图3(a)所示。齿轮磨损时，其振幅显著增大，但没有明显的冲击振动信号产生，如图3(b)所示。齿轮断齿时，其振幅显著增大，并且有明显的周期性冲击振动信号产生，如图3(c)所示，经计算，该冲击频率与断齿齿轮的公转频率相同。

3 齿轮故障特征提取

3.1 小波相关滤波法降噪

以齿轮箱存在断齿时的振动信号为例进行分析。小波变换采用Daubechies系列的dB4小波基，其具有正交、紧支和对不规则信号较为敏感的特点[7]。当小波分解层数为4时，得到4层分解系数，根据1.1节中的算法流程对原信号进行小波相关降噪。各层阈值比分别为t(1)=1.1，t(2)=1.2，t(3)=1.4，t(4)=1.6。降噪前后振动信号如图4所示。其中：图4(b)为经小波相关滤波法降噪后的重组信号；图4(c)为利用Matlab自带的ddencmp函数对原始信号进行一维小波降噪后的信号；图4(d)为利用wden函数对原始信号进行小波分析降噪后的信号。表1为3种降噪方法的信噪比，可以看出：WTCF降噪效果优于其他2种降噪方法。

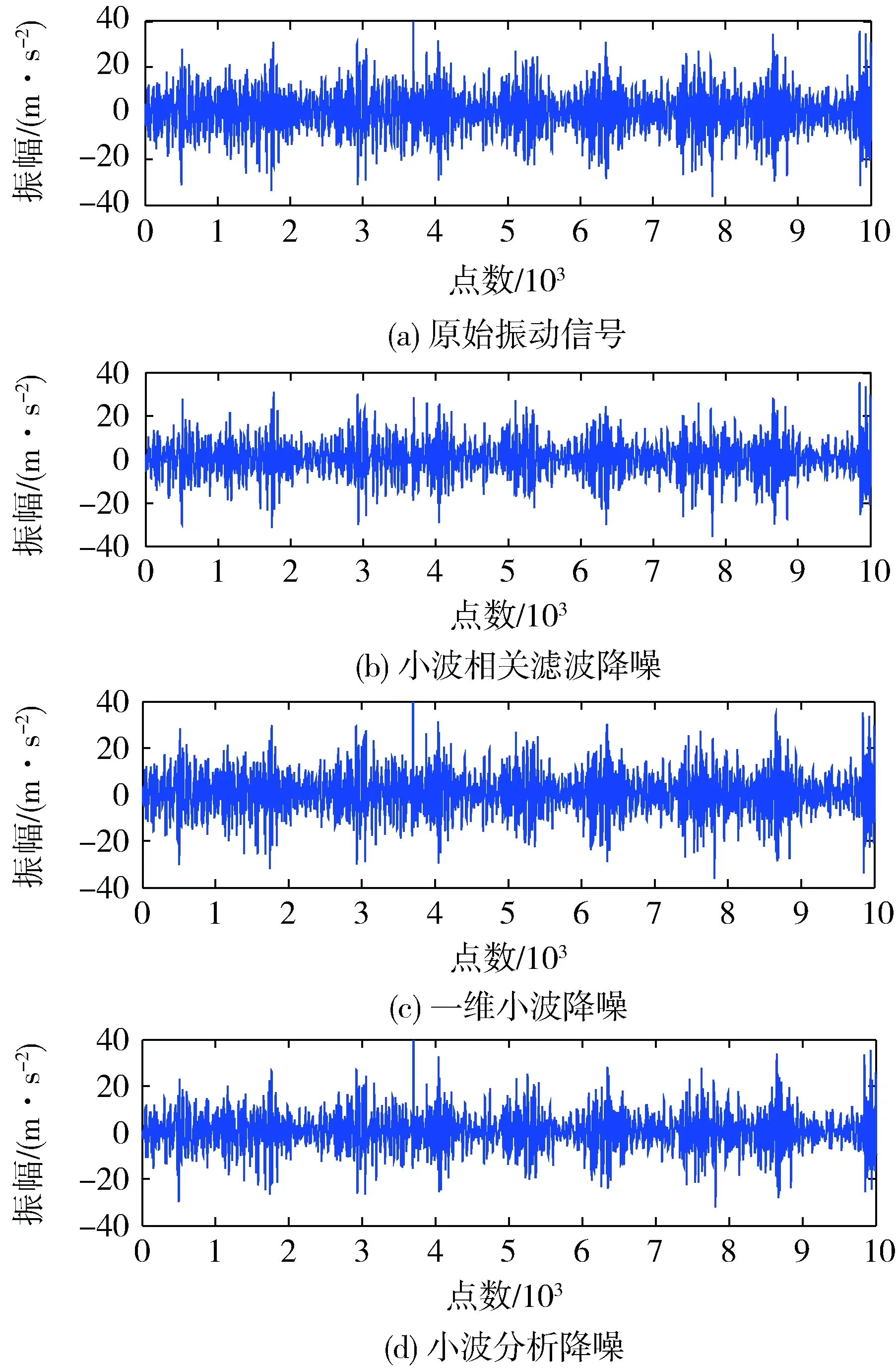
图4 降噪前后振动信号

表1 3种降噪方法的信噪比

图5为降噪前后断齿状态下振动信号的频谱，主要分析0～3 000 Hz以内的信号频率,可以看出:原始信号中除了217 Hz挡位啮合频率和451 Hz常啮合频率外，还存在大量1 500 Hz以上的高频成分，主要是齿轮发生断齿时由于箱体振动而产生的噪声；经过降噪处理后，齿轮的挡位啮合频率、常啮合频率更加凸显，而原信号中1 000 Hz以上幅值较小的噪声信号频率得到了较好抑制，进一步说明小波相关滤波法能够较好地消除噪声的影响。

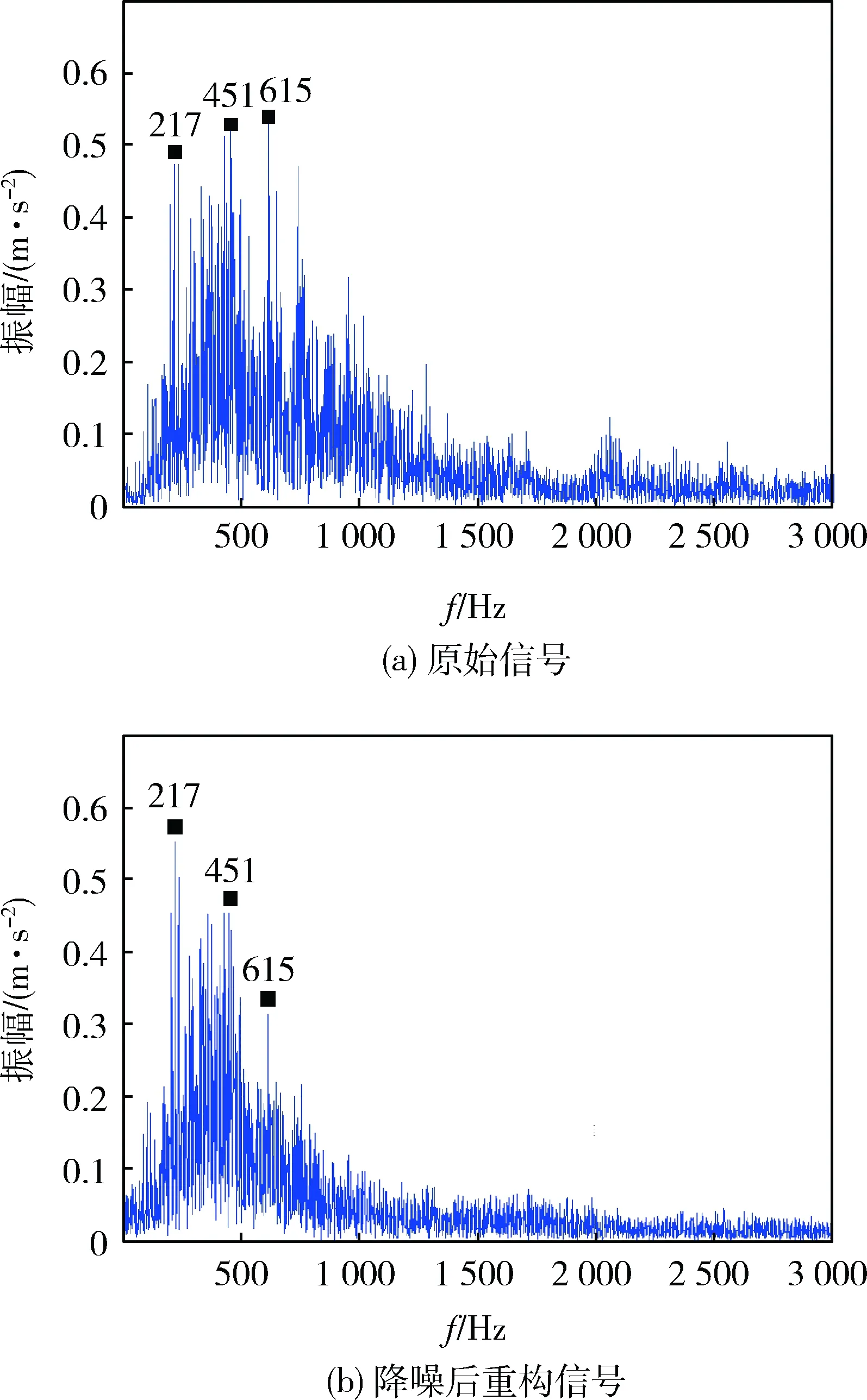
图5 降噪前后断齿状态下振动信号的频谱

3.2 排列熵计算

根据排列熵的有关原理，计算降噪后重构信号的排列熵。令m=5，τ=11，时间序列长度L=1 250，大于1个周期内所采集的点数。根据L值将样本内的采样点进行时间序列划分，每1 250个点为一组，共分为80个组，由此计算排列熵变化曲线。3种状态下降噪前后振动信号排列熵变化曲线如图6-8所示。

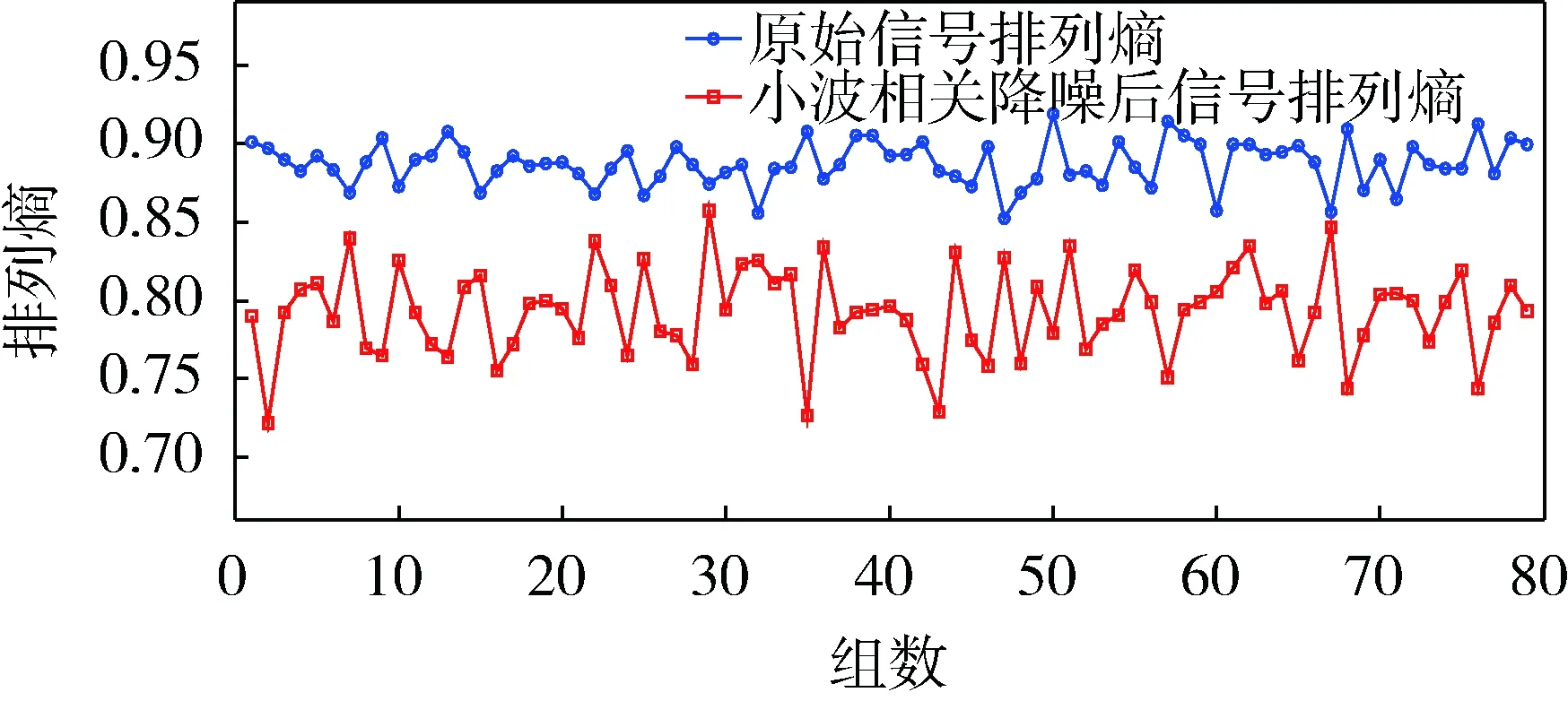
图6 正常状态下降噪前后振动信号排列熵变化曲线

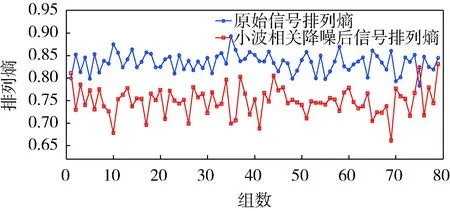
图7 磨损状态下降噪前后振动信号排列熵变化曲线

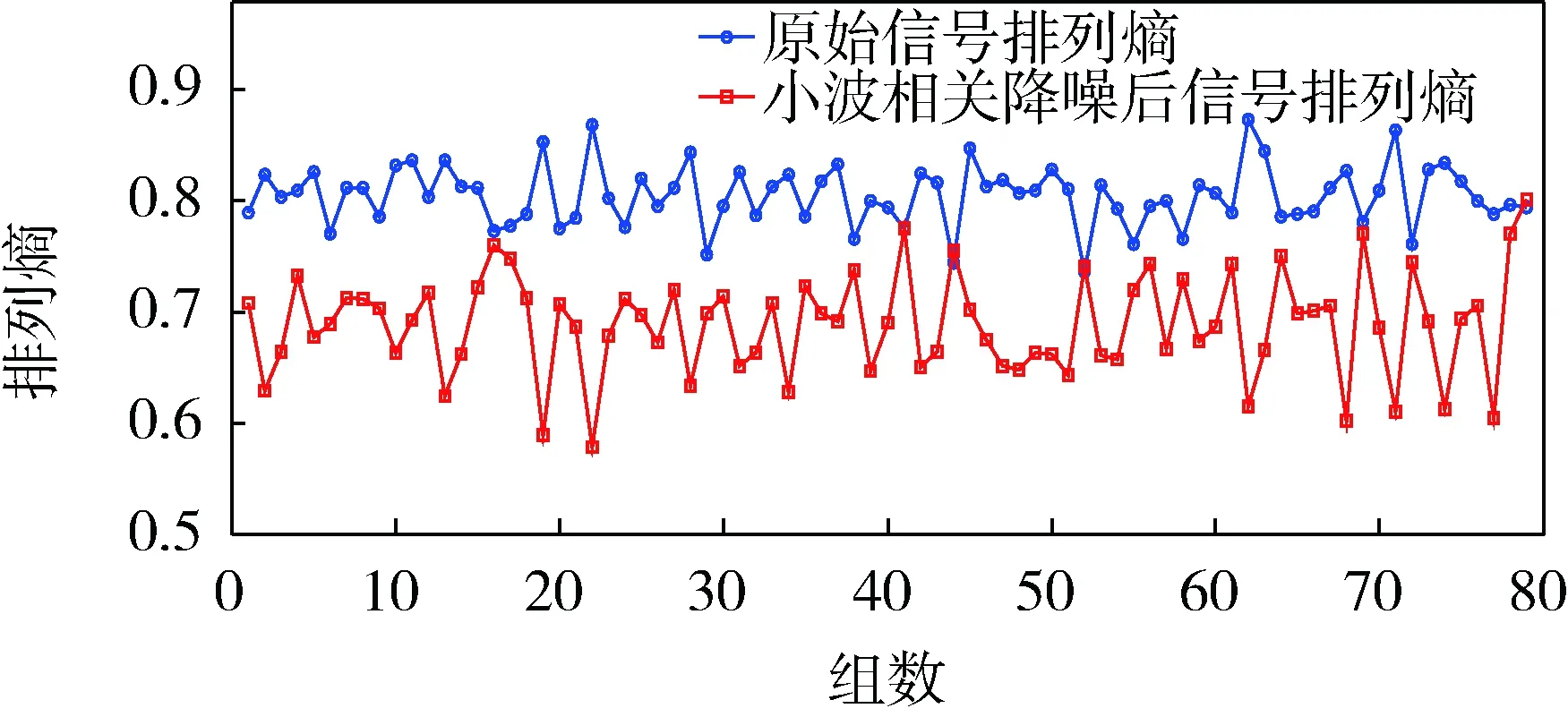
图8 断齿状态下降噪前后振动信号排列熵变化曲线

排列熵反映一维时间序列复杂度，在此可以反映齿轮振动信号的复杂度。在转速、负载相同时，齿轮振动信号的排列熵越大，振动信号越随机；反之，振动信号越平稳。进一步计算信号排列熵均值(MEAN)和均方根值(RMS)，结果如表2所示。结合图6-8和表2可以得出以下结果。

1) 齿轮在正常、磨损、断齿3种状态时，齿轮箱垂直方向上振动信号的排列熵有所不同，正常时最大，磨损时次之，断齿时最小。这是因为正常齿轮振动信号在各个频带上的能量分布比较均匀，能量分布的不确定性较大；当发生磨损或断齿故障时，能量分布主要集中在固有频率段，不确定性相对减小。

表2 齿轮不同状态下振动信号排列熵均值和均方根植

2) 小波相关降噪后信号排列熵均值要小于原始信号，但其均方根值却大于原始信号。这是因为降噪后信号频率成分减少，信号的能量分布集中且更具有规律性；但排列熵对冲击信号敏感，齿轮振动信号包含的冲击会使排列熵波动变大。

进一步研究负载对排列熵的影响，对于正常状态的齿轮箱，从空载开始，每50 N·m一个等级，逐渐加载，直到载不动为止，振动信号如图9所示。对采集到的信号进行小波相关降噪和排列熵计算，令m=4，τ=3，时间序列L=1 024，排列熵随负载的变化情况如图10所示。

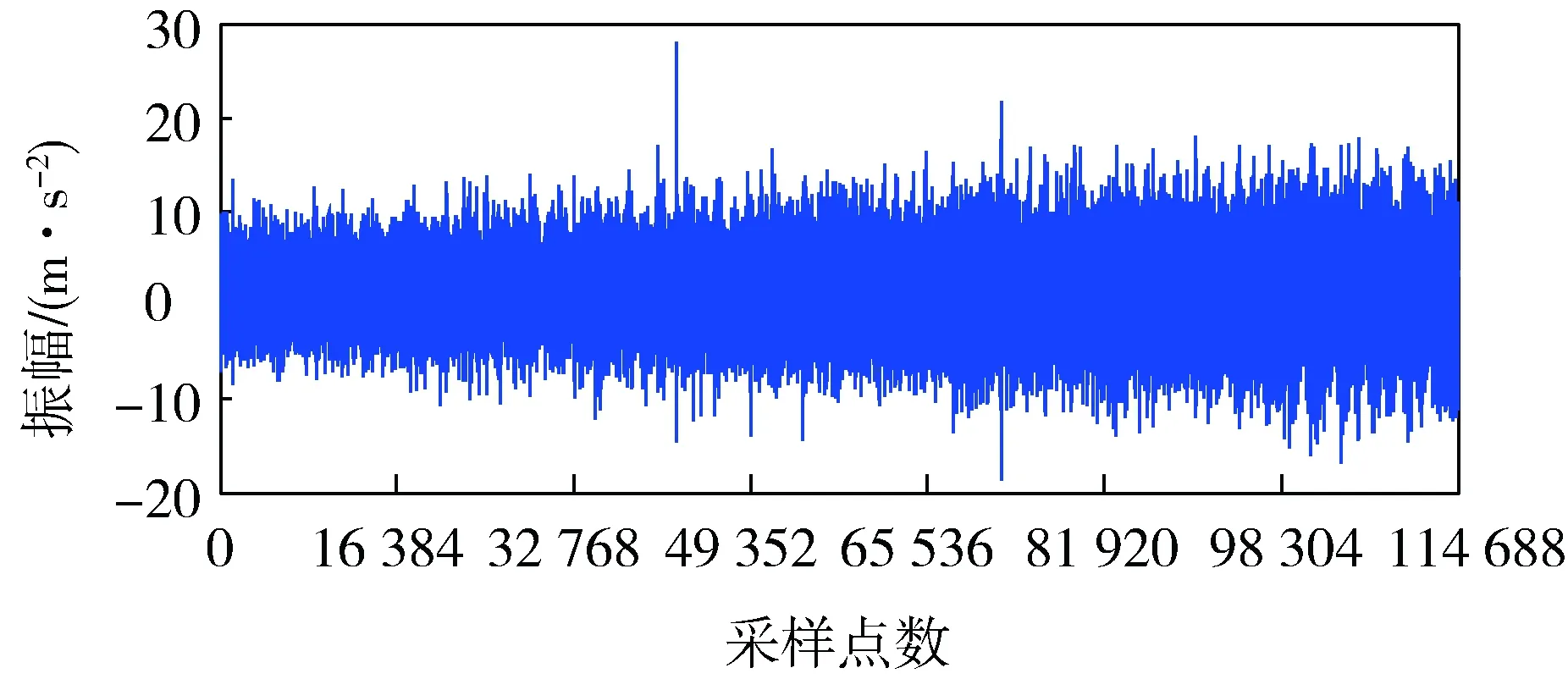
图9 负载逐渐增大的振动信号

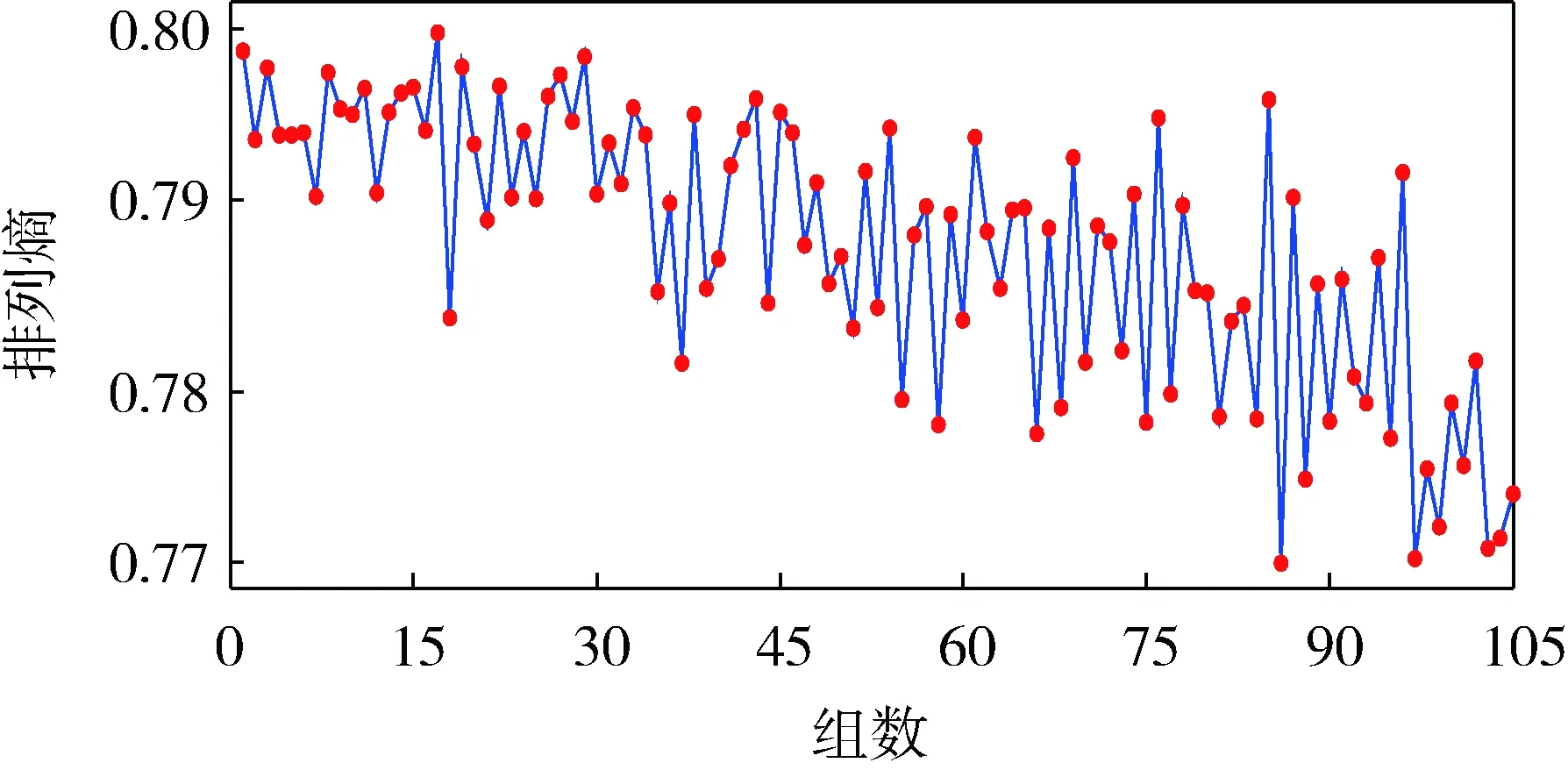
图10 排列熵随负载的变化情况

表3是不同负载信号小波相关排列熵均值和均方根值，可以看出:随着负载的增大，小波相关排列熵均值减小，而均方根值增大。这是由于负载增大时，齿轮因受力而啮合更加紧密，虽然振动信号幅值增大，但周期性更加明显。这与实际中负载增大时齿轮箱高频噪声会有所减小的现象相一致。

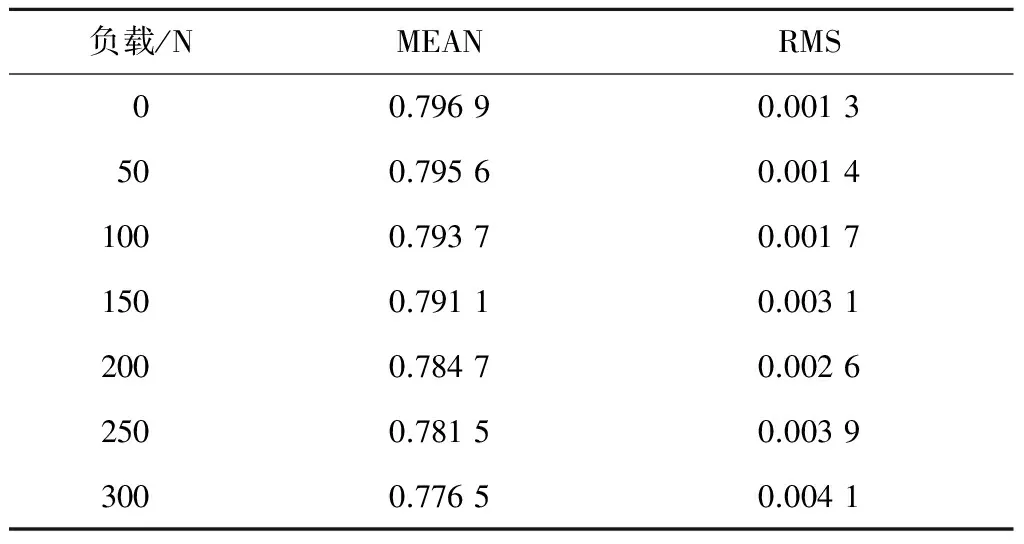
表3 不同负载信号小波相关排列熵均值和均方根值

[1] 徐敏，虞和济，张瑞林．设备故障诊断手册[M]. 西安：西安交通大学出版社，1998：407-434．

[2] 冯辅周，安钢，刘建敏．军用车辆故障诊断学[M]. 北京：国防工业出版社，2007：477-484．

[3] 李舜酩，李香莲．振动信号的现代分析技术与应用[M].北京: 国防工业出版社，2008：77-88．

[4] 葛哲学，沙伟．小波分析理论与MATLAB实现[M]. 北京：电子工业出版社，2007：454-479．

[5] 印欣运，何永勇，彭志科，等．小波熵及其在状态趋势分析中的应用[J].振动工程学报，2004，17(2)：165-169．

[6] Liu B, Riemenschneider S, Xu Y. Gearbox Fault Diagnosis Using Empirical Mode Decomposition and Hilbert Spectrum [J]. Mechanical Systems and Signal Processing，2006，20(3)：718-734．

[7] 杨宇，于德介，程军圣. 基于经验模态分解的滚动轴承故障诊断方法[J]. 中国机械工程，2004，15(10)：908-911.

[8] 冯辅周，司爱辉，饶国强，等．基于小波相关排列熵的轴承早期故障诊断技术[J].机械工程学报，2012，29(3)：73-79．

[9] Yang H T，Liao C C. A De-noising Scheme for Enhancing Wavelet-based Power Quality Monitoring Systems[J]. IEEE Transactions on Power Delivery，2001，16(3)：353-359．

[10] 孙野．虚拟试验技术及其在坦克变速箱故障机理研究中的应用[D].北京：装甲兵工程学院，2012．

(责任编辑:尚彩娟)

Fault Feature Extraction from Gearbox Vibration Signal Based on Wavelet Correlation Permutation Entropy

CONG Hua1, CUI Chao2, JIANG Peng-cheng2, LIU Yuan-hong2, FENG Fu-zhou2

(1. Department of Science Research, Academy of Armored Force Engineering, Beijing 100072, China; 2. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

In order to solve the problems of low signal-to-noise ratio and difficulties in feature extraction from gearbox vibration signals, a fault feature extraction method based on wavelet correlation permutation entropy is proposed. The gear vibration signals of different working conditions are denoised using wavelet domain spatial filter which has adaptive function. Then the permutation entropy change curves of denoised signals are calculated using permutation entropy algorithm and the fault features are extracted by comparing the wavelet correlation permutation entropy characteristic values under different conditions. Finally vibration signals in three different conditions of normal, wear and broken teeth by transmission test platform are collected for analysis and computation, the experimental results show that the proposed method can extract gear fault feature effectively.

gear; fault feature; wavelet correlation; permutation entropy

1672-1497(2015)04-0031-05

2014-11-04

军队科研计划项目

丛 华(1966-)，男，教授，博士。

TP206+.3; TJ81+0.321

A

10.3969/j.issn.1672-1497.2015.04.007