假设检验在军事工程应用中的若干问题

夏佩伦，李本昌，李 博

（海军潜艇学院，山东 青岛 266042）

假设检验在军事工程应用中的若干问题

夏佩伦，李本昌，李 博

（海军潜艇学院，山东 青岛 266042）

对假设检验这一统计学工具在军事工程应用中值得注意的若干问题进行了探讨，包括假设的设置、检验门限的设置和统计量的构造等，这些问题在理论上有一些一般的指导，但在实际工程应用中，需要根据具体问题进行设计，这中间涉及一些技巧和经验，也容易出现一些常被忽视的问题。指出了这些问题，并给出了在实际工程中应用好假设检验的一些建议。

假设检验，充分统计量，奈曼-皮尔逊引理，沃尔德序贯观测器，费歇尔-奈曼准则

0 引言

假设检验是统计推断的有力工具，在实际问题中有着广泛应用。军事系统中的许多问题也可归结为假设检验问题，如一般作战指挥系统中的目标探测与跟踪、目标识别、信息融合、作战决策等环节都存在诸多的判决问题，可以运用假设检验的工具来处理。

比如，目标探测实质上就是要根据目标探测传感器的探测结果来判断“目标是否存在”，这是假设检验经典的应用例子［1-2］。军事目标识别则一般是根据以某种手段获取的目标特征信息来回答“目标为何类型”、“目标属敌方还是我方”等问题［3-4］。目标跟踪过程中，则经常要回答诸如“目标是否机动”、“目标以何种模式机动”、“有几个目标”等判断性问题［5-7］。军事信息融合常会遇到诸如“同一传感器两次测量的信号是否属于同一目标”、“不同传感器的目标航迹是否属于同一目标”之类的判决问题。这些判决问题因涉及诸多的不确定性因素而无法给出确切的判决结果，因而需要借助统计学工具来加以解决。

假设检验是一个实践性较强的工具，它的应用有很强的技巧性。运用不当，检验结果将不可靠。而在工程实践中，人们恰恰容易忽视这一点。本文将就假设检验在军事工程应用中容易出现的问题加以探讨，包括假设的设置、检验门限的设置和统计量的构造等，目的是引起有关工程技术人员的重视。此外，本文还一般性地探讨了假设检验应用的一些技巧。

以下首先将对假设检验加以简单介绍，而后对上述提到的几个应用问题进行讨论。有关假设检验理论更详细的内容可以参考数理统计和信号检测理论方面的文献，如文献［1-2，8-10］。假设检验应用方面的文献可参考文献［11-12］。

1 假设检验

假设检验就是基于样本观测值和一定规则在统计意义下决定某些假设中何者为真的过程。典型的假设检验问题是以下的二元假设检验问题：

其中参数集Θ0和Θ1（Θ0∩Θ1≠Ø，这里Ø表空集）表征了某一随机变量z的可能分布，当然，已知z的一样本观测值集（称为z的实现，并用Z表示）。问题是要利用Z来判断两个假设H0和H1谁为真。

由于Z的元素也是随机变量，因此，不能指望利用Z得到的检验结果百分之百地正确。检验错误不可避免。检验错误有两类，分别称为第1类错误和第2类错误，其发生概率分别为：

为了利用统计学的工具对H0和H1进行检验，需要利用Z构造检验统计量T（Z）。方法是根据需要设定T（Z）的门限值λ，当T（Z）大于λ时，拒绝H0；当T（Z）小于λ时，拒绝H1，如图1所示。即

*拒绝H0：当T（Z）＞λ时；

*拒绝H1：当T（Z）＜λ时。

图1中f（Z|Hj）为假设Hj（j=0，1）的似然函数。

图1 判决准则

对此，会提出如下要求：①要求所构造的统计量T（Z）能充分反应Z中所包含的关于参数θ的信息；②上述两类错误发生的概率能尽量小。理论和实践都表明，满足这样的要求是困难的。在实践中这需要很好地进行折衷，而这样的技巧正是一些工程技术人员所缺乏的。

2 假设设置

从两类错误的角度讲，H0和H1的地位是不对称的。因此，H0和H1的选择不是任意的，而是要考虑实际问题对两类误差的要求。著名的奈曼-皮尔逊引理（Neyman-Pearson lemma）表明，可以将第一类错误控制在任意小，但第2类错误却无法控制。当然可以在给定最大的第1类错误允许概率的条件下得到最小的第2类错误的概率，但这个概率可能很大。这是我们所不希望的，但对此无能为力。因此，H0和H1的设置不是任意的。应该慎重地考虑，以便能够控制我们更为关注的一类错误的概率。

由于第1类错误的概率可以控制，因此，有以下的选择H0的3个原则：①使后果更为严重的错误成为第1类错误；②当需要得到对某一陈述的有力支持时，将这一陈述的否定设置为H0；③将普遍接受的假设设置为H0。

以目标检测为例，一般以“目标不存在”为原假设，“目标存在”为备择假设。这样，第1类错误就是目标实际不存在而检验结果是目标存在，即常说的“虚警”；第2类错误就是目标实际存在而检验结果是目标不存在，即所谓的“漏检”。这种假设设置自然是受一般的信号检测影响的。运用在军事系统中，这种假设设置值得考虑。目标检测虽然本质上也是一类信号检测问题，但有其特殊性。事实上，在很多目标检测的应用场合，更关心“漏检”概率而不是“虚警”概率。例如，对于诸如防空系统、反导系统、预警系统、侦察系统，对“漏检”概率有更高的要求，因为从错误的严重性来看，宁愿受“虚警”之扰，而不愿被敌方导弹轻易突防。因此，往往要求将“漏检”概率控制在一定的限度内。

在另一些系统中，H0和H1的选择不是这么明显。例如，多传感器目标航迹关联时，以“航迹关联”还是“航迹不关联”作为原假设不能一概而论。两类错误，即误把“关联”当“不关联”或误把“不关联”当“关联”，在很多情况下所造成后果的严重性是类似的。即都是态势的不真实反映，从而对指挥员和武器系统产生误导。对于这样的情况，H0和H1的选择并不特别重要，不论如何选择，关键是选择合适的检验门限，以便在两类错误概率间达成折衷。不过，在具体的系统中，H0和H1的选择还是很值得考虑的。例如，在潜艇的多传感器目标航迹关联中，认为以“航迹关联”作原假设为好。这时的第1类错误是把“关联”当作“不关联”。潜艇指控系统处理能力有限，所携武器数量也很有限。在这样的条件下，不能容忍因航迹关联错误造成的虚假目标耗费系统的处理能力和误导武器，在密集目标环境更是如此。在另外的应用场合，如目标中既有敌方目标又有己方目标，而且希望区分它们时，可能更不希望把“不关联”当“关联”，因此，此时应该以“航迹不关联”作原假设。

目标机动检测问题是类似的。以“目标机动”还是“目标未机动”作为原假设，需要具体情况具体考虑。如果系统有很好的机动目标处理能力、武器对目标运动参数精度有很高的要求（比如直航武器），往往能容忍把“目标未机动”误作“目标机动”的错误；反之，如果系统本身的处理能力有限，或者所携武器具有适应机动目标的能力（如灵巧武器），则可能宁愿发生“目标机动”当“目标未机动”的错误，而不是相反。

3 检验门限的设置

理论上讲，检验门限（即λ）的设置是很简单的。在构造好检验统计量T（Z）的条件下，只要给定允许的第1类错误的发生概率（用α表示），λ是很容易确定的。方法是：

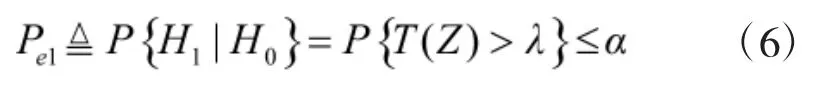
满足T（Z）＞λ的Z的集合称为拒绝域，表明若样本观测值属于该域时，应该拒绝H0。因此，检验门限的设置实际上也就是确定拒绝域。归根结底，还是要确定第1类错误的允许发生概率。然而，这个概率要确定得合适并不容易，这正是实际问题的难点所在。

难点的关键还是在于两类错误的密切关联性。不能不顾第2类错误的发生概率而仅仅追求第1类错误的低概率。已经知道，α可以控制在任意小，问题是Pe2可能很大。事实上，检验门限设置得合适与否，关键是看它在难以判断的困难检验情况下（即两种假设为真的可能性很接近的情况下），是否仍能保证较高的检验功效。比如，在多传感器目标航迹关联应用中，当两传感器的两条目标航迹分得很开时，关联检验是很容易的。这时即使α控制得很小，Pe2可能仍不大。而当两条目标航迹比较接近时，检验将变得困难得多。这时α若设定得太小，Pe2肯定很大。这样做在实际中肯定是不合适的。如此看来，检验门限的设置是需要结合实际问题、综合考虑、反复试验方能解决的问题。

检验门限设置另一个值得注意的问题是门限与样本大小的关系。军事实际问题中，样本往往是在不断积累的，即Z中的元素不断增加。比如，随着对目标搜索跟踪的进程，关于目标的信号越来越多，就是用于检验的样本越来越大。因此，本质上说，用于军事目的的假设检验问题多为序贯假设检验问题（即样本数量可变；相应地，样本数量不变称为非序贯假设检验问题）。

容易想象，序贯假设检验问题的检验门限应该是与样本大小有关的。并且在对两类错误的同等容忍程度的条件下，该门限应随样本的增大而减小。然而，工程上经常是采用固定的门限。一般而言，这种做法是不能接受的。

对于上述提到的实际中两种假设为真的可能性很接近（从而很难判断）的情况，如果条件允许的话，可以采用序贯的检验方式，即不断增加观测样本，即不断引入新的观测信息，直至能有效地进行判断为止。沃尔德序贯观测器（Wald sequential observer）就是采用了这样的机制［13］。它为T（Z）设定两个门限值λ1和λ2（λ1＜λ2），而不是一个，如图2所示。每次观测后，根据计算的T（Z）的结果，作出如下3个判决中的一个：

*拒绝H0：当T（Z）＞λ2时；

*拒绝H1：当T（Z）＜λ1时；

*无法确定是拒绝H0还是H1，等待新的观测样本，继续检验：当λ1＜T（Z）＜λ2时。

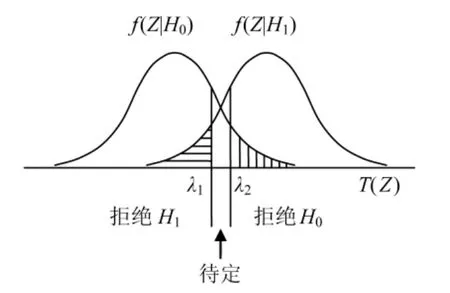
图2 双判决门限的情形

4 统计量的构造

任何不直接包含总体未知因素的关于样本Z的函数（严格地说，应为波雷尔函数（Borel function））都是统计量。因此，构造统计量可以有相当大的随意性。在所关心的假设检验问题中，既然要用统计量来对关于未知量θ的假设进行检验，总是希望所构造统计量能充分包含Z中关于θ的信息。即要求T（Z）是充分统计量。事实上，在另一类重要的统计推断问题——参数估计中，也有这样要求。但这一基本要求却常被一些工程技术人员所忽视。

统计量的充分性可通过其定义直接来判断。设T（Z）是关于未知量θ的统计量，若总体累积分布函数F［Z|T（Z），θ］与θ无关，则T（Z）是关于未知量θ的充分统计量。即，取定T（Z）后的上述条件分布函数的表达式中应不包含θ。

更方便、常用的判断方法是利用费歇尔-奈曼准则（Fisher-Neyman criterion，即因子分解定理）。该准则指出，T（Z）是关于未知量θ的充分统计量的充要条件是：Z的联合密度函数（似然函数）可按下面的形式分解：

其中：zi（i＝1，…，n）为Z的元素，g［·］仅通过T（Z）依赖于Z，而h（·）与θ无关。

可以证明，θ的极大似然估计总是其充分统计量的函数。因为这个原因，工程上常用θ的极大似然估计作其统计量。

前面提到的奈曼-皮尔逊引理说明，在给定第1类错误允许概率条件下的一个最优检验（最大功效检验），使得到第2类错误的发生概率最小。该引理还给出了具体的检验统计量，这个统计量同似然函数有关。它对构造统计量应该是很有指导意义的。该引理指出，对于简单假设检验问题（θ0和θ1皆只有一个元素），在给定的条件下Pe1≤α，极大化Pd（或极小化Pe2）的最优检验为：若L＜λ，则拒绝H1；或，若L＞λ，则接受H1。其中，L为称为似然比的检验统计量，其定义如下：

而λ则由给定的α确定，即

因此，似然比统计量总是一种可供选择的统计量。

5 结束语

以上讨论了假设检验应用中常碰到的几个问题。可以看出，应用好假设检验这一工具，需要有良好数学理论基础，更需要有结合实际问题、充分发挥这一工具优势的技巧。为此，在实际问题中注意本文提到的几个问题是有好处的。应该指出的是，根据不同的具体应用，值得考虑的问题还很多。比如关于检验结果的解释问题，表面看来，只要统计观测值落入拒绝域，就可认为H0为假、H1为真；反之，只要统计观测值落入接受域，就可认为H0为真、H1为假。实际上并没有这么简单。类似的技巧，除了统计学知识的支撑外，还有赖实践摸索和经验积累。

［1］Van T H L.Detection，Estimation and Modulation Theory，Vol.I［M］.New York：John Wiley and Sons，1969.

［2］Whalen A D.Detection of Signal in Noise［M］.New York：A-cademic Press，1971.

［3］Waltz E，Llinas J.Multisensor Data Fusion［M］.Norwood，MA：Artech House，1990.

［4］Wilson G B.Some Aspects of Data Fusion［C］//Harris C J，White I（eds.），Advances in Command，Control&Communication Systems，London：Peter Peregrinus，1987.

［5］夏佩伦.目标跟踪与信息融合［M］.北京：国防工业出版社，2010.

［6］Bar-Shalom Y，Li X R.Multitarget-Multisensor Tracking［M］.Storrs，CT：YBS Publishing，1995.

［7］Bar-Shalom Y，Fortmann T E.Tracking and Data Association［M］.New York：Academic Press，1988.

［8］浙江大学数学系高等数学教研室.概率论与数理统计［M］.北京：高等教育出版社，1979.

［9］何迎晖，闵华玲.数理统计［M］.北京：高等教育出版社，1989.

［10］Bar-Shalom Y，Li X R，Kirubarajan T.Estimation with App lications to Tracking and Navigation［M］.New York：John Wiley and Sons，2001.

［11］Blackman S S.Multi-Target Tracking with Radar Applications［M］.Norwood，MA：Artech House，1986.

［12］Sadjadi F.Hypothesis Testing in a Distributed Environment［J］.IEEE Trans.Aerospace and Electronic Systems，1986，AES-22（3）：134-137.

［13］Wald A.Sequential Analysis［M］.New York：John Wiley and Sons，1947.

Some Issues Concerning Applications of Hypothesis Testing in Military Engineering

XIA Pei-lun，LI Ben-chang，LI Bo
（Navy Submarine Academy，Qingdao 266042，China）

This paper studies some issues concerning applications of hypothesis testing in military engineering，including hypothesis choices，test threshold determination，and construction of sufficient statistics.There are some general instuctions in the literature in handling these issues.In real engineering applications，they often need careful designing，which involves both expertises and experiences.Various problems may also arise in such applications，which are often neglected.These issures and problem are emphasized and suggestions for taking good advantage of the hypothesis testing tool in engineering applicaions are given.

hypothesis testing，sufficient statistic，Neyman-Pearson lemma，Wald sequential observer，Fisher-Neyman criterion

O212.1；E919

A

1002-0640（2015）03-0100-04

2014-01-18

2014-03-22

夏佩伦（1964- ），男，江西吉安人，教授。研究方向：目标跟踪与信息融合。