基于四元数法的反辐射武器飞行仿真研究

申军岭，徐 海，崔连虎

（解放军91336部队，河北 秦皇岛 066326）

基于四元数法的反辐射武器飞行仿真研究

申军岭，徐 海，崔连虎

（解放军91336部队，河北 秦皇岛 066326）

在开发反辐射武器攻击目标的三维飞行仿真系统中或分析处理三维运动数据时，针对传统的运动姿态旋转方法存在计算繁琐、旋转不均匀性及平衡环锁定等局限问题，采用四元数法可以避免这些局限，并且几何意义明确，计算简单。因此，提出在飞行仿真系统中利用四元数法来实现反辐射武器的运动姿态及飞行速度矢量的旋转，在飞行仿真试验中实现了飞行轨迹变化光滑连续的合理效果，仿真结果表明四元数法简化了矢量旋转计算模型，优化了解算性能，能够很好地应用于反辐射武器飞行仿真试验中。

反辐射武器，飞行运动仿真，四元数

0 引言

目前，雷达的主要威胁来自于反辐射武器的攻击，因此，对反辐射武器和雷达之间的攻防对抗研究成为当前试验研究的重要内容，雷达抗反辐射武器攻击的主要措施是采用诱饵装置诱偏反辐射武器，这就涉及到雷达保护概率的计算和样本量的选取，由于样本量的选取直接影响可信度，在实际试验中，实弹靶试具有成本高、保密性差、样本量有限的特点，不能实际反映诱饵对反辐射武器的诱偏效果。而全数字仿真试验具有试验环境和过程可控、数据录取容易、试验重复性好、效费比高和保密性好等优点，因而成为雷达诱饵抗反辐射武器攻击性能评估的一项重要技术手段。

那么如何有效逼真地对反辐射武器飞行运动进行仿真就成为影响试验结果的重要因素，在传统的反辐射武器飞行仿真中，通常采用基于欧拉角的方法来表示运动物体的姿态和方向。使用欧拉角来描述运动物体的姿态简单直观，但使用这种方法时存在一个非常明显的缺陷，就是当物体绕某个轴旋转90°时，会导致物体旋转自由度的减少，即万向节死锁问题［1］。因此，如果要在两个方位欧拉角间进行插值遇到90°时，就会导致系统出现旋转路径的错误。本文设计采用基于四元数方法表示反辐射武器运动模型的三维姿态及其旋转，解决三维空间反辐射武器飞行运动仿真中出现姿态和旋转问题，以保证反辐射武器飞行运动仿真中运动姿态平滑连续变化和飞行轨迹逼真。

1 四元数的基本原理

四元数实际上是对复数同系统的扩展，由爱尔兰数学家William Harmilton所创造，他把复数由2D扩展到3D，在计算机图形学中，特别是矢量旋转和球面线性插值方面可以用四元数来构造变换的工具［2］。

1.1 四元数定义

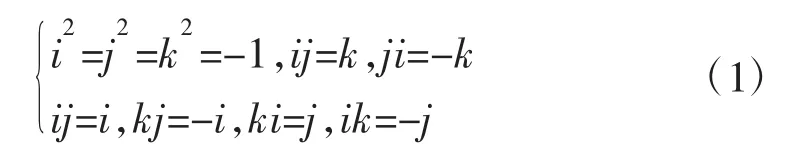
与之对应的四元数为［w，（x，y，z）］，标准复数的许多性质都可以运用在四元数上，四元数提供了一种3D运算的记法。把3D空间上的点（x，y，z）扩展到四元数空间，其相应的记法为［0，（x，y，z）］，更为重要的是四元数也能用于旋转3D矢量，这是在3D矢量旋转中引入四元数的主要原因［3］。

1.2 用四元数作旋转变换

与旋转变换相关的一些定义：

（1）四元数的模：

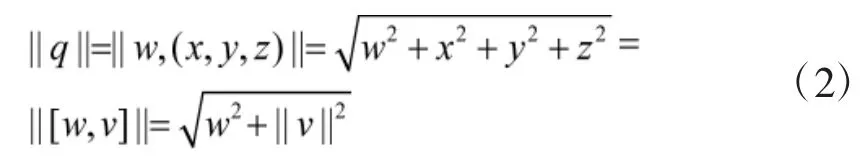
（2）四元数的共轭，四元数q=［w，v］的共轭q*，通过将四元数的矢量部分变负获得：

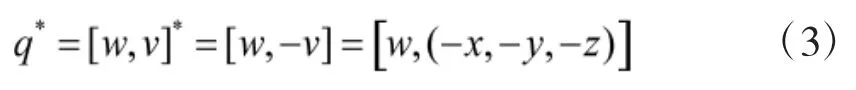
（3）四元数q的逆q-1，定义为：

从表4可以看出，在刀具长度相同的情况下，随着刀具直径的增加，换能器谐振频率有较大下降，最大应力值有小幅降低；在刀具直径相同时，随着刀具长度变长，换能器谐振频率和最大应力值逐渐降低，刀具直径越大，下降的幅度也越剧烈。不同尺寸刀具下，换能器的位移节点位置基本没有变化，与不安装刀具的换能器位移节点位置相同，但在刀具直径为7mm，长度在40mm以上时，位移节点位置从49mm处跳跃到53mm处，已经不能满足换能器的安装固定要求。

（4）四元数的乘法：

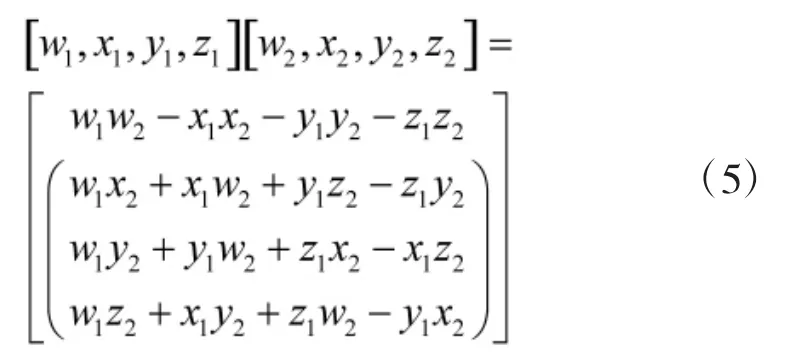
如果设有一个3D空间中矢量p=［0，（x，y，z）］，一个四元数q=［cosθ，n*sinθ］，执行以下的乘法：

则得到的p'正是将矢量p绕矢量n旋转2θ弧度的结果。

上式的旋转矩阵可以将一个3D矢量绕任意轴n旋转，旋转角为2θ，将qpq-1展开就会发现它与矩阵式旋转其实是等价的，但四元数法只用了4个数就可以表示方位，而矩阵转矢法需要9个数，提高了运算效率。

2 反辐射武器攻击雷达诱饵飞行运动过程

多点源抗反辐射武器攻击，反辐射武器在接近目标的飞行过程中，在距离较远时，多点源都位于反辐射导引头分辨角△θR范围内，导引头没法分辨各点源，跟踪雷达和诱饵形成的能量中心［4］；当反辐射武器接近点源时，各点源与导引头瞄准轴方向之间的夹角越来越大，当其中一点源与导引头瞄准轴方向的夹角等于△θR/2时，导引头开始分辨出目标，下一时刻该点源将脱离出导引头的视场，该点源对反辐射导引头不构成干扰。反辐射武器在飞行过程中，导引头视场角内总会经过由多点源变成三点源、两点源和单点源情形，最后选择单个点源进行摧毁攻击。反辐射武器分辨出某个辐射源后将以最大过载向新的跟踪目标引导（自动跟踪），修正初始失误，但这时反辐射武器距新的跟踪目标很近，受过载能力约束，最终以偏离跟踪目标一定的距离落地。其飞行原理如图1所示，反辐射武器高度为H，攻击角度α（弹轴指向多站能量中心），雷达至多点能量质心O的距离为L。反辐射武器的最终弹着点为O1。在临界位置上即导引头分辨出目标位置，由于某一随机因素，导引头分辨出雷达（A点）的方向，以最大机动过载aM向雷达（A点）飞去，飞过的最大水平距离S=OO1。

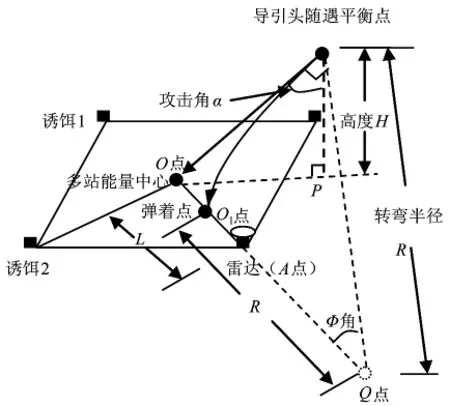
图1 反辐射武器攻击目标原理

由此可见，反辐射武器攻击雷达诱饵的飞行运动过程中将对目标源进行数次判别，瞄准方向时刻在变化，速度方向和导引头瞄准方向不同，则反辐射武器需要时刻修正瞄准误差，修正飞行轨迹，以实现最大程度的摧毁目标。为了分析雷达抗反辐射武器攻击时诱饵的诱偏效果，则需要模拟反辐射武器的飞行运动过程，这就涉及到反辐射武器飞行过程中的姿态调整和旋转问题，为了进一步分析，将反辐射武器的飞行时间离散化，研究每一时刻和下一时刻反辐射武器的飞行状态，进行动态仿真，基本复现反辐射武器的飞行运动过程。

2.1 反辐射武器飞行运动仿真

根据对反辐射武器的飞行时间离散化原理［5］，其飞行状态示意图如图2所示，设tk时刻反辐射武器所在的位置为Ak（xk，yk，zk），此时导引头实测多点源能量中心方向为AkMk，而反辐射武器飞行速度方向为AkMk-1，经过时间△t，反辐射武器到达Ak+1（xk+1，yk+1，zk+1）。其中AkMk-1与AkMk间的夹角为αk，AkMk-1与AkMk+1间的夹角为αz。

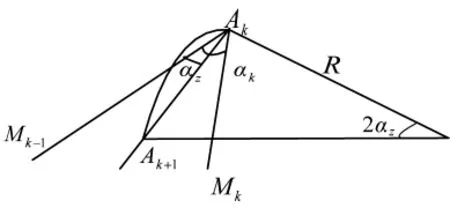
图2 反辐射武器飞行状态示意图

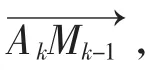
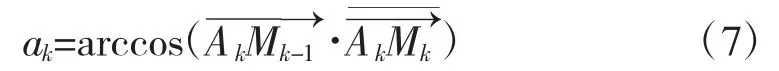
△t时间内，反辐射武器能够转过的最大角度为：

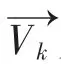
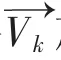
2.2 四元数法在反辐射武器飞行运动仿真中的应用

根据2.1节分析的反辐射武器飞行运动过程的基本原理，在开发雷达诱饵抗反辐射武器攻击的运动仿真系统时，反辐射武器的运动轨迹需要随时间的不断变化而变化，因此，要得到下一时刻反辐射武器的速度矢量，就要根据反辐射武器当前的速度方向和瞄准方向求解下一时刻的速度矢量，传统的迭代法、矩阵转矢法以及欧拉角法由于计算复杂、参数需求多等原因不能满足反辐射武器的飞行运动仿真，而四元数法只需要将当前的速度矢量和瞄准方向转换为四元数形式，再根据四元数矢量旋转方法进行矢量旋转计算，获取旋转数据，最终获得平滑逼真的飞行运动轨迹，直观反映反辐射武器攻击目标时的运动过程，为试验、科研人员进行数据分析，结果评估提供了快捷准确的新型试验方法。

2.3 基于四元数法的旋转算法实现

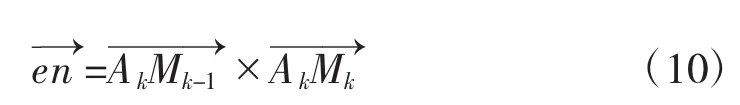
则四元数转矢为：

进而可以计算得到tk+1时刻反辐射武器所在的位置坐标（xk+1，yk+1，zk+1），从而模拟反辐射武器飞行过程中的轨迹点和最终落点。

3 仿真实例验证

仿真参数设置：地面共有4个辐射源，包括3个诱饵和一部雷达，反辐射武器初始攻击位置随机产生，雷达位置为（0，0，0）m。3个诱饵与雷达成典型菱形布阵，间距为300 m，导弹初始速度为3 MHz，反辐射武器初始发射方向并不完全对准地面辐射源，有关对抗双方的参数比较多，这里仅列出部分。整个仿真过程从模拟反辐射武器搜索截获目标信号开始，在分辨出某个辐射源之后，开始最大过载机动转弯攻击，转弯过程仿真算法采用四元数法优化，从而模拟反辐射武器的攻击航迹运动特点。图3是采用四元数法实现的反辐射武器攻击四点源目标的飞行航迹图实例。图4是选取100个随机攻击模式下反辐射武器攻击目标最终弹着点与雷达和诱饵之间的相对位置关系。

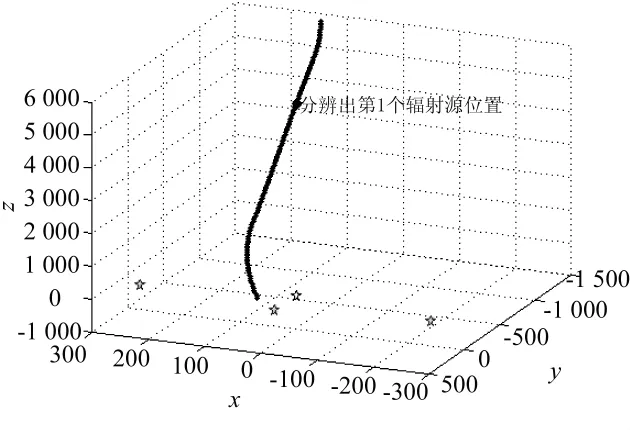
图3 反辐射武器攻击目标仿真航迹图

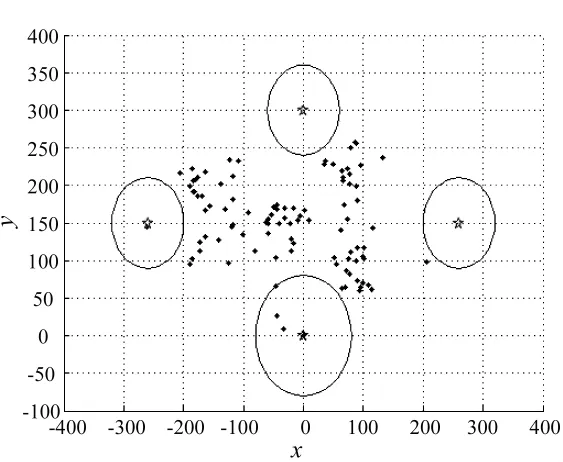
图4 反辐射武器攻击目标弹着点示意图

由图3可见四元数法能够实现反辐射武器飞行仿真中，飞行运动轨迹的平滑旋转，逼真模拟反辐射武器攻击雷达诱饵系统的飞行航迹。图4给出了反辐射武器的弹着点与雷达诱饵的相对位置关系，并经matlab仿真计算得出雷达生存概率为94%，雷达诱饵系统联合生存概率为93.06%，结果表明，基于四元数的飞行旋转方法成功模拟各种随机条件下反辐射武器的飞行航迹，其弹着点分布规律、雷达保护概率、雷达诱饵系统联合生存概率与理论计算值和实际打靶结果相符，从而得出四元数法能够应用于反辐射武器与雷达诱饵系统攻防对抗过程中，能够很好地模拟反辐射武器的飞行航迹，并且具有几何意义明确，计算简单，运算量小的优点，能够很好地应用于反辐射武器攻击雷达诱饵系统的仿真试验中。

4 结论

本文研究了四元数方法在三维空间反辐射武器攻击雷达诱饵飞行航迹仿真中的应用。利用四元数的方法实现飞行运动仿真中模型的矢量旋转，将四元数法方便快捷直观的特点与运动模型相结合，实现了反辐射武器模型飞行运动仿真中的平滑旋转，减少了计算量，节省了计算时间，省时高效。结果表明，四元数方法能够应用于反辐射武器攻击雷达诱饵的飞行航迹仿真中，有效地解决了飞行航迹中矢量旋转问题，为飞行航迹仿真中的矢量旋转计算提出了新的可靠简便的计算方法。

［1］薛源，徐浩军，胡孟权.基于四元数法飞行运动方程的逆向仿真算法［J］.空军工程大学学报，2010，11（3）：6-11.

［2］肖伟，梁久祯.基于四元数的3D物体旋转及运动插值［J］.系统仿真学报，2012，24（3）：624-627.

［3］谢荣，鲁海燕.基于四元数的船舶运动姿态仿真研究［J］.中国造船，2011，52（4）：146-151.

［4］周伟光，罗积润.雷达配置诱饵对抗反辐射导弹的仿真［J］.电子与信息学报，2010，32（6）：1370-1376.

［5］周颖，甘德云，许宝民.反辐射武器攻防对抗理论与试验［M］.北京：电子工业出版社，2012.

Research on Application of Quaternion in Flight Simulation of Anti-Radiation Weapon

SHEN Jun-ling，XU Hai，CUI Lian-hu
（Unit 91336 of PLA，Qinhuangdao 066326，China）

In the three dimensional flight simulation system of anti-radiation weapon attack or analysis of 3D motion data，the traditional motion of rotation method exits in calculation complated and have balance ring locking limitation.Quaternion method can avoid these limitations and have clear geometric meaning with simple calculation，therefore this paper puts forward quaternion method to achieve motion attitude and flight velocity vector rotation in the anti-radiation weapons flight simulation system and realize the reasonable effect of flight attitude anti-radiation weapons are smooth and continuous change in anti-radiation weapons flight simulation，The results of application show that the quaternion method can improve the calculation efficiency and apply in flight simulation of antiradiation weapons.

anti-radiation weapon，flight simulation，quaternion

TP391.9

A

1002-0640（2015）03-0142-04

2014-01-11

2014-03-21

申军岭（1983- ），男，新疆伊犁人，硕士。研究方向：导弹武器系统仿真。