基于稀疏贝叶斯学习的DOA估计*

董天宝，汪海兵，曾芳玲

（电子工程学院，合肥 230037）

基于稀疏贝叶斯学习的DOA估计*

董天宝，汪海兵，曾芳玲

（电子工程学院，合肥 230037）

针对基于l1范数约束的稀疏表示DOA（Direction Of Arrival）估计算法对初始参数较为敏感的问题，提出了一种基于稀疏贝叶斯学习的DOA估计算法。首先通过信号来波方向的空间采样构造冗余字典，将阵列信号处理中的DOA估计信号模型转化为压缩感知中的稀疏重构信号模型。然后基于经验贝叶斯推理的方法，将待估计的稀疏系数值用方差未知的联合高斯分布描述，而未知的方差值决定了待估计系数的稀疏性。通过观测数据估计得到未知的方差，进而得到信号的DOA估计值。仿真结果表明，提出的算法有较高估计精度，并且对非相干信源和相干信源都具有较好的估计性能。

波达方向，稀疏表示，贝叶斯学习

0 引言

DOA估计广泛应用于雷达、通信、超声波、语音和水下探测等众多领域，一直是信号处理领域的研究热点。经过数十年研究，到目前为止，针对于高斯噪声下的DOA估计已经存在大量超分辨算法，这些算法大致可以分为3类：第1类以Capon［1］和AE［2］为代表，通过自适应设计与接收数据相匹配的空间滤波器，获得非参数化的空域谱；第2类是以MUSIC［3］（MUltiple SIgnal Classification）和 ESPRIT［4］（Estimation of Signal Parameters via a Rotational Invariance Technique）为代表的子空间类算法，通过利用信号空间的低秩结构来获得信号的DOA估计，子空间类算法在信噪比较高、快拍数较多、信源间相关性不强时可以获得较高的估计精度；第3类是最大似然算法［5］，包括确定最大似然和统计最大似然两种，这类算法具有最佳的统计性能，但是需要适当迭代初始值来保证收敛于全局最小值。

近年来在信息论和信号处理领域中发展起来的压缩感知理论［6］表明，当信号可以压缩或稀疏表示时，可以用一个与变换矩阵不相关的测量矩阵将一个高维信号投影到一个低维空间上，然后将信号的稀疏表示问题转化为一个最优化问题，原信号能够以很高的概率精确重构。基于该理论，可以采用低于奈奎斯特频率的采样率对信号进行采样，从而使得该理论具有极大的吸引力。许多学者对该理论展开了研究，目前该理论已广泛应用于图像处理、无线通信、盲信号处理等诸多领域。

Malioutov等人［7］于2005年提出的l1-SVD算法可以说是稀疏表示模型应用于DOA估计的奠基性算法，该算法首先在方位域进行等间隔采样，由这些角度对应的导向矢量构成冗余字典，然后对接收数据矩阵进行奇异值分解，利用若干个（等于信源个数）大特征向量组成测量信号，结合冗余字典建立联合稀疏表示模型，并利用二阶锥规划和内点法求解模型，最后根据估计矩阵中非零行索引获得信源DOA估计。在信源个数预知的前提下，可以获得精确的估计结果，但若信源个数未知，则形成的空间谱中伪峰较多，造成估计偏差。此外，该算法的计算量巨大，表现出与信源个数和方位域采样份数乘积的三次方成比例关系。随后，相关学者也相继提出了许多基于稀疏表示的DOA估计算法［8-11］，这些算法在进行稀疏信号重构时大多采用的是基于l1范数约束的最优化方法，但这些算法的一个局限性就是在进行优化问题求解时涉及到一个正则化参数的选取问题，大多数算法都是采用人工设置的方法，从而限制了该类算法的实际应用。针对该问题，本文提出在构建好用于DOA估计的信号模型后，采用稀疏贝叶斯学习的方法实现DOA估计，该方法采用经验贝叶斯学习方法，首先将待估计的稀疏系数表示成含有未知参数的先验分布，而该未知参数可以通过观测数据学习得到，从而可以实现自适应DOA估计。

1 DOA估计信号模型

假设有M个阵列，K个远场窄带信号入射到阵列，阵列接收数据x（t）可以表示为：

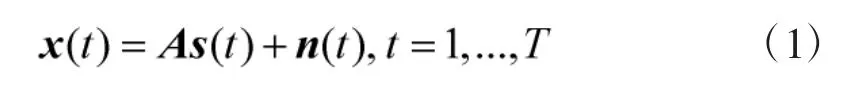
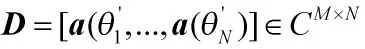
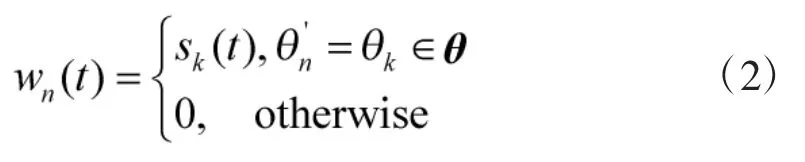
式（2）说明w（t）中非零元素的位置与信源的真实方位角存在一一对应关系，只要得到w（t）中K个非零元素值的索引即可获得信源的DOA估计。于是基于稀疏表示的DOA估计信号模型为：

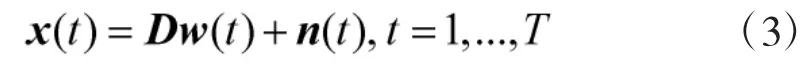
当采用矩阵形式表示时，可以写为：

2 基于稀疏贝叶斯学习的DOA估计算法

稀疏贝叶斯学习最早是由Tipping［12］提出的，其主要思想是基于经验贝叶斯原理。本节将该算法扩展到复数域，并应用于DOA估计问题。在阵列信号处理算法中，通常需要处理的信号都是以解析信号形式表示的，即式（3）和式（4）中的各部分通常都是以复数形式表示的，因此，在采用贝叶斯推理方法解决稀疏重构问题时，相应的先验假设及推导过程必须以复数形式描述。假设式（4）中的噪声是加性复高斯随机过程，且与信号不相关，噪声方差大小为λ。xi.表示X的第i行，x.j表示X的第j列，wi.表示W的第i行，w.j表示W的第j列，本文中如不做特殊说明，都采用这种表示方式，于是可以得到下面的似然函数：

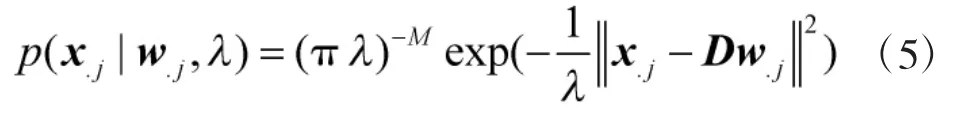
该式表示的是一个多维复高斯分布，其中的范数‖x‖2=xHx。依据经验贝叶斯原理，假设式（4）中W的第i个行向量的先验分布是一个维数为T，均值为0，方差为γi的复高斯分布：

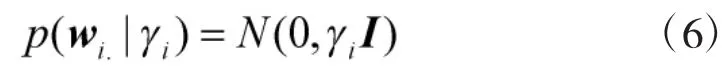
其中γi在贝叶斯推理中称为超参数，是一个未知的参数，该参数可以通过观测数据估计得到。由W行向量的先验分布假设可以得到W的先验分布为：

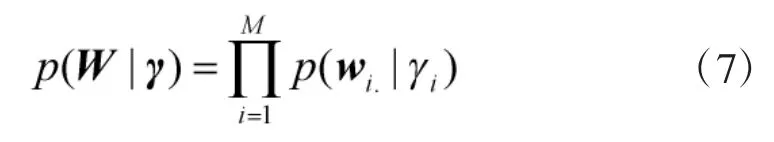
其中γ=［γ1，…，γM］T。根据式（5）表示的似然函数及W的先验假设分布，由贝叶斯公式可以推导得到W的第j个列向量的后验概率分布：

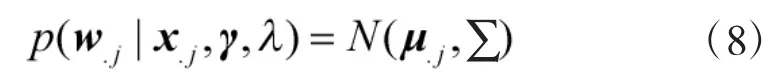
由该表达式可知，W的第j个列向量满足复高斯分布，其中μ.j，∑分别表示均值向量和协方差矩阵，

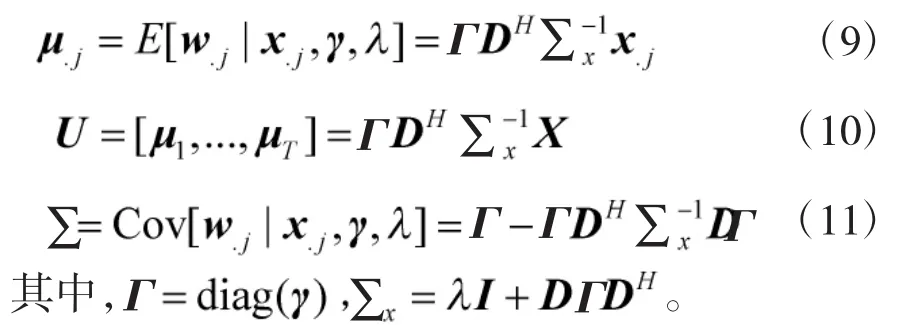
由式（8）可知，由于W满足复高斯分布，因此，如果能获得μ.j的估计，也就得到了w.j的估计。对于稀疏重构问题，其目的就是要得到W的估计，而对于DOA估计问题，由前一节所描述的信号模型可知，只需要得到W中非零行向量的索引就可以得到DOA的估计。由式（9）可知，W的先验分布中的方差γ是信号能量的度量，同时决定了W的稀疏度，即当γi趋于零时，对应的μ.j中的第i个分量等于零。因此，只要得到了γ的估计，由γ中非零值的索引就可以得到信号的DOA估计。为了得到γ的估计，采用证据最大化方法，也称为第二类最大似然法。第二类对数似然函数可以由下式得到：

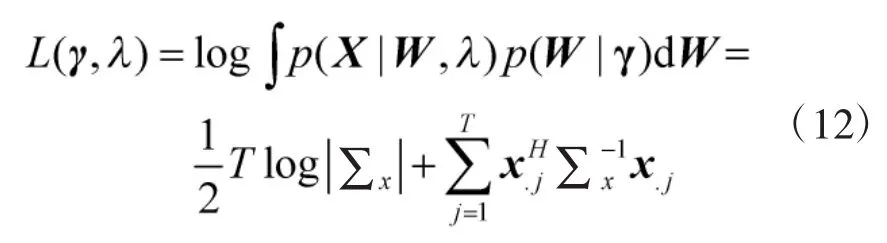
于是，由第二类最大似然法可以得到γ和λ估计的迭代公式：

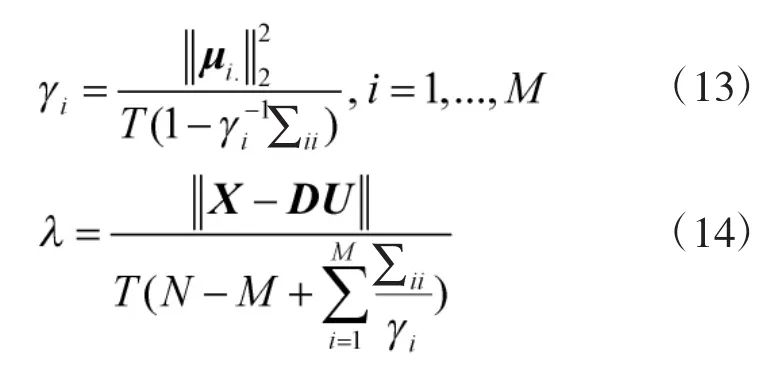
其中∑ii表示式（11）对应的协方差矩阵对角线上的第i个元素。当迭代收敛得到γ的估计后，由γ中非零值的索引即可得到信号的DOA估计。实际中由于噪声及各种误差的影响，通常取γ中较大极值的索引得到信号的DOA估计。

由前面的分析，可以得到基于稀疏贝叶斯学习的DOA估计算法的步骤：

（1）初始化γ和λ；

（2）进行迭代运算：

①由式（10）、式（11）计算均值和协方差矩阵；

②由式（13）、式（14）更新γ和λ；

③重复①、②，直到γ收敛。

（3）由γ中较大极值的索引得到信号的DOA估计。

3 仿真分析

在本节中，通过计算机仿真验证本文提出算法的DOA估计性能。仿真中，选择M=8个阵元的均匀线阵，阵元间距为半个信号波长。假设有K个等功率远场窄带信号入射到该阵列，信号和噪声均假设为零均值、独立同分布复高斯随机变量。

对于本文提出的算法和L1-SVD算法，在方位域［0°，180°］范围内1°以为间隔均匀采样生成冗余字典D。MUSIC算法在方位域［0°，180°］内以1°为间隔进行谱峰搜索。角度估计的衡量标准选择均方根误差（Root Mean Square Error，RMSE），定义为：

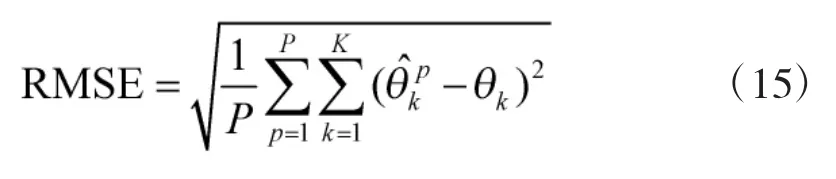
实验1：独立信源情况下的实验

假设3个相互独立信号从不同方向入射到阵列上，入射角分别为50°、80°和120°，信噪比均为10 dB。下页图1为快拍数为200时，分别采用不同DOA估计算法得到的空间谱对比。从图中可以看出，本文算法与MUSIC算法能正确分辨出两个信号，且DOA估计精度相比于l1-SVD算法都较高，但本文算法峰值更为尖锐。l1-SVD算法可以分辨出两个信号，但估计误差相对较大。图2为快拍数为1时各算法DOA估计得到的空间谱对比，由该图可知，当快拍数只有1个时，MUSIC算法已经无法实现有效的DOA估计，而本文算法和l1-SVD可以实现对来波信号方位的有效估计，本文提出的DOA估计算法的估计精度更高。图3是快拍数为200时在不同信噪比下的角度估计精度比较，由该图可知，与其他两种算法相比，本文提出的算法在低信噪比条件下具有更高地估计精度。

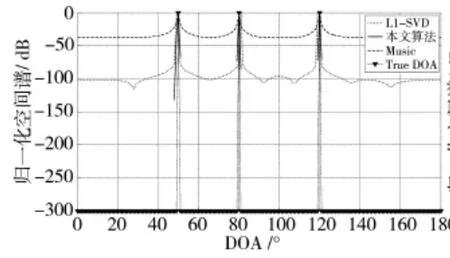
图1 快拍数为200时3种算法的归一化空间谱

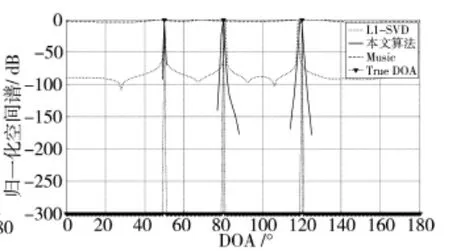
图2 快拍数为1时3种算法的归一化空间谱

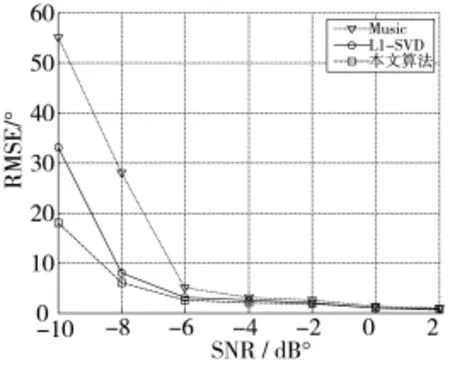
图3 不同信噪比条件下3种算法的估计精度比较

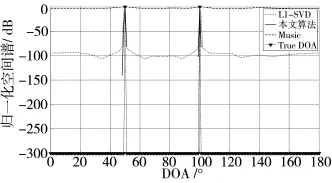
图4 相干信源时3种算法的归一化空间谱

实验2：相干信源情况下的实验

假设有2个完全相干的信号从不同方向入射到接收阵列，信噪比均为10 dB。图4为快拍数为200时，分别采用不同DOA估计算法得到的空间谱对比。从图中可以看出MUSIC算法无法对相干信源的来波方向进行有效估计，而本文算法和l1-SVD算法能估计出两个相干信源的来波方向，其中本文提出的算法估计精度更高。

4 结论

本文提出了一种基于稀疏贝叶斯学习的DOA估计方法，将DOA估计问题转化为稀疏信号重构问题，构造合适的稀疏表示信号模型，采用经验贝叶斯推理的方法实现了参数自适应的DOA估计，提高了算法的实用性。仿真结果与传统的MUSIC算法相比，本文算法在低信噪比条件下具有更高的估计精度，在单快拍条件下也能以较高精度估计出信号的来波方向，并且本文算法对非相干信源和相干信源都有效。与同样基于稀疏表示的l1-SVD算法相比，本文算法具有更高的估计精度。

［1］Capon J.High-resolution Frequency-wavenumber Spectrum Analysis ［J］. Proceedings of IEEE，1969，57（8）: 1408-1418.

［2］Stoica P，Li P，Li J.A New Derivation of the Apes Filter［J］. IEEE Signal Processing Letters，1999，6（8）:205-206.

［3］Schmidt R.Multiple Emitter Location and Signal Parameter Estimation［J］.IEEE Transactions on Antennas and Propagation，1986，34（3）:276-280.

［4］Roy R，Kailath T.Esprit-estimation of Signal Parameters via Rotational Invariance Techniques［J］.IEEE Transactions on Acoustics，Speech and SignalProcessing，1989，37（7）: 984-995.

［5］Stoica P，Sharman K.Maximum Likelihood Methods for Direction-of-Arrival Estimation［J］.IEEE Transactions on A-coustics，Speech and Signal Processing，1990，38（7）: 1132-1143.

［6］Donoho D L，Compressed S.Technical Report［M］.Stanford University，2004.

［7］Malioutov D，Cetin M，Willsky A.A Sparse Signal Reconstruction Perspective for DOA Estimation with Sensor Arrays［J］.IEEE Transactions on Signal Processing，2005，53（8）: 3010-3022.

［8］Yin J H，Chen T Q.Direction-of-Arrival Estimation Using a Sparse Representation of Array Covariance Covariance Vectors［J］.IEEE Transaction on Signal Processing，2011，59（9）:4489-4493.

［9］贺亚鹏，李洪涛，王克让，等.基于压缩感知的高分辨DOA估计［J］.宇航学报，2011，32（6）:1344-1349.

［10］郭莹，孟彩云.基于稀疏表示和约束优化的波达方向估计方法［J］.计算机应用，2012，32（8）:2106-2108，2127.

［11］冯莹莹，程向阳，邓明.基于稀疏表示的信号DOA估计［J］.计算机应用研究，2013，30（2）：537-540.

［12］Tipping M E.Sparse Bayesian Learning and the Relevance Vector Machine［J］.Journal of Machine Learning Research，2001（1）:211-244.

DOA Estimation Based on Sparse Bayesian Learning

DONG Tian-bao，WANG Hai-bing，ZENG Fang-ling
（Electronic Engineering Institute，Hefei 230037，China）

A Direction-Of-Arrival（DOA）estimation algorithm based on sparse Bayesian learning is proposed，which is less sensitive to initial parameters than other DOA estimation algorithms based on l1-norm.First，a DOA estimation model is transformed to one sparse signal reconstruction model by constructing a redundant dictionary from spatial samples of the interested signals.Then，sparse parameters are represented by a union Gaussian distribution with unknown variances using empirical Bayesian analysis method，and the unknown variances determine the sparsity of the parameters.Finally，the unknown variances are estimated from observation data and the DOAs of the interested signals are estimated. Simulation results show that the proposed algorithm can estimate the DOAs of signals with high accuracy，and it is effective for both coherent signals and noncoherent signals.

DOA，sparse representation，bayesian learning

TN911.6

A

1002-0640（2015）03-0042-04

2014-01-18

2014-03-29

国家自然科学基金（61272333）；安徽省自然科学基金资助项目（1208085 MF94）

董天宝（1976- ），男，辽宁鞍山人，讲师，博士。研究方向：阵列信号处理。