基于小波分析与Burg功率谱的主轴故障诊断研究*
□ 印 嘉 □ 王仕旭
阿坝师范学院物理与电子科学系 四川 汶川 623002
在管道输送行业中,往复式活塞隔膜泵是主要动力输出设备,保障它的安全运行至关重要。其中,主轴是往复式活塞隔膜泵的重要部件之一,主轴一旦出现故障,将造成巨大的经济损失,甚至人员伤亡[1]。因此,对往复式活塞隔膜泵主轴的故障诊断研究有着重要的意义。
由于往复式活塞隔膜泵主轴故障具有多元性、不确定性和并发性等特点[2],因此,对故障的研究十分困难,而且设备的振动信息蕴含了丰富的运行状况和特征信息[3]。本文提出了一种采用小波分析与Burg功率谱相结合的故障诊断方法,通过分析和研究设备的振动信号来实现往复式活塞隔膜泵主轴故障诊断研究。首先对采集到的原始振动信号进行小波分析处理,去除噪声,提高信噪比,再对去噪后的振动信号进行Burg功率谱分析,最后通过研究和分析振动信号的功率谱特征变化情况,实现了对设备故障有效的诊断和研究。
1 小波分析
小波变换具有自适应性,可对信号进行局部分析,并且小波分析的对象不仅是平稳信号,对时变信号一样有效。信号的小波变换是信号与基小波的相似性运算,小波系数大小反映这种相似性的强弱[4][5]。
在小波分析中,主要讨论的函数空间为L2(R)。L2(R)指 R 上平方可积函数构成的函数空间[5],即:
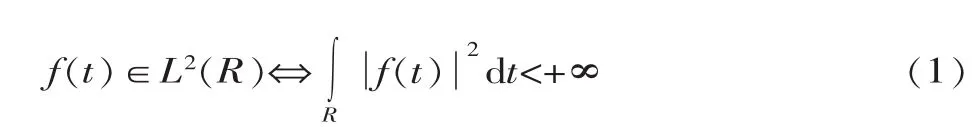
若 f(t)∈L2(R),则称 f(t)为能量有限的信号,L2(R)也常称为能量有限的信号空间。
如果 ψ(t)∈L2(R),其傅里叶变换为 ψ(w)满足容许性条件(Admissible Condition):
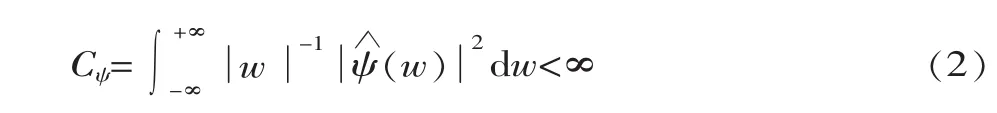
式中:w为频率。
Cψ为有界,则称ψ为一个基小波或者母小波(Mother Wavelet)。将母小波经过伸缩和平移后,可以得到一个小波序列:
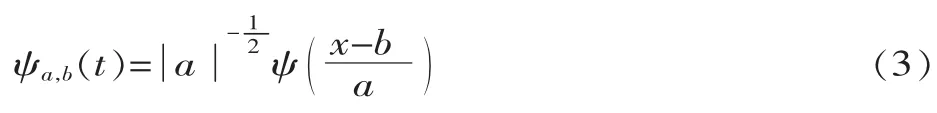
式(3)中,a、b∈R,且 a≠0,称 a 为伸缩因子,b 为平移因子。 关于基小波 ψ 的连续小波变换(Wψf)(a,b)可以定义为:
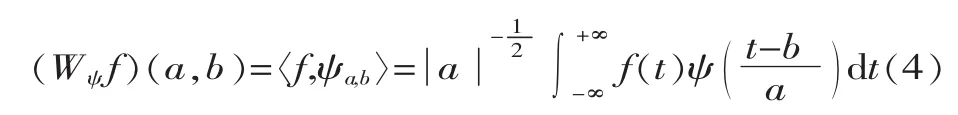
显然,变换后的函数是二维的,即小波变换把原来的一维信号变换成二维信号,以便分析信号 (或者函数)的时频特性。
对信号去噪实质上是抑制信号中的无用部分、增加信号中的有用部分的过程,信号小波去噪的过程为:
首先,选择一个合适的小波确定分解的层次,进行分解计算;
然后,选择一个恰当阈值对各层的小波系数进行阈值化处理;
最后,根据小波分解的小波系数进行重构。
2 Burg功率谱
功率谱是利用已观测到的一定数量样本数据估计一个平稳随机信号的功率谱密度[6],因其能够分析信号的能量随频率变化的分布特征,在许多实际应用中功率谱的分析与估计已变得越来越重要了[7]。
功率谱Burg方法是一种最为广泛的经典功率谱估计方法之一[8]。Burg功率谱又称为最大熵谱估计,其表达式为:
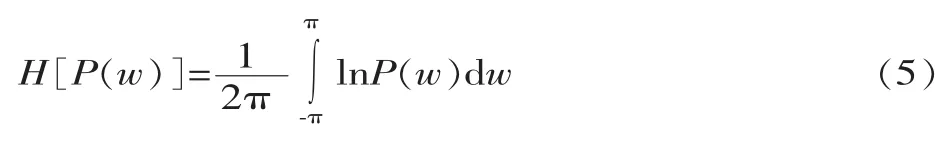
式中:P(w)为功率谱密度函数。
Burg最大熵谱估计可以表述为求功率谱P(w),使其在约束条件下:
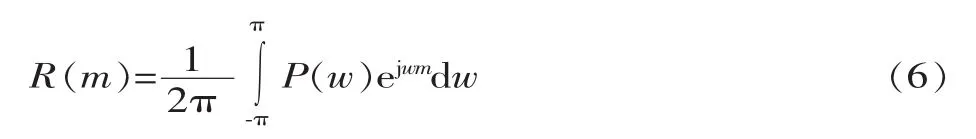
式中:m=0,±1,...,±p,这样能够使谱熵 H[P(w)]达到最大。
对这一具有约束条件的优化问题采用Lagrange乘子法求解,得到:

式中:λk为Lagrange乘子。
3 实验仿真验证
本文采用美国Case Western Reserve University发布的振动信号数据为实验仿真数据,进行仿真实验和验证,证明方法的可行性与有效性。轴承转速为1797 r/min,采样频率为12kHz,采样点为1024。图1为故障振动信号,图2为正常振动信号。通过查看图1和图2的频率特征,可以得到振动幅值发生了明显的变化,说明设备确实出现了异常状况,但是无法确定具体故障特征,因此需要对原始信号作进一步的分析和处理。
为了进一步对故障振动信号进行分析与研究,可以通过进行Burg功率谱来实现。图3为故障振动信号的Burg功率谱,图4为正常振动信号的Burg功率谱。不难发现,正常时的Burg功率谱和故障时的Burg功率谱的整体变化趋势是一致的,谱峰清晰,故障特征明显,但是不易快速定位故障频率特征,所以不能作为设备故障诊断的主要依据。
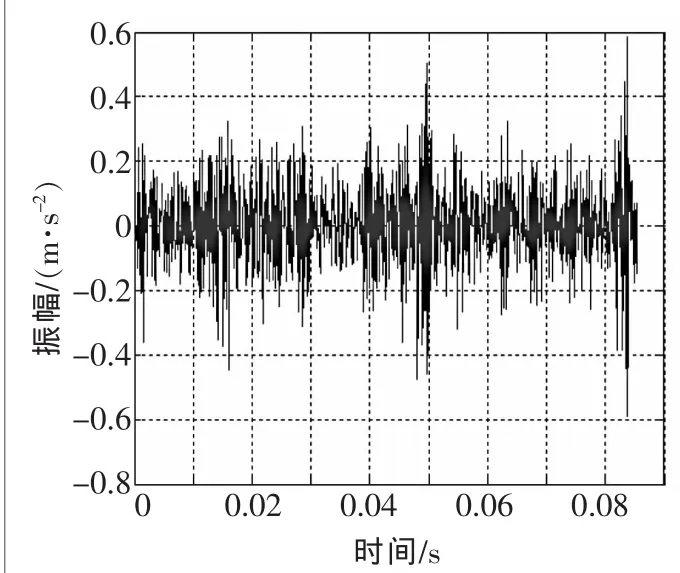
▲图1 故障振动信号
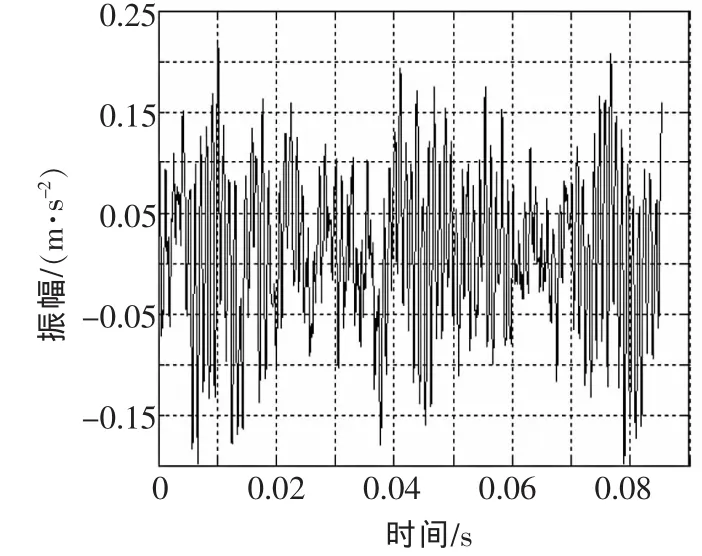
▲图2 正常振动信号
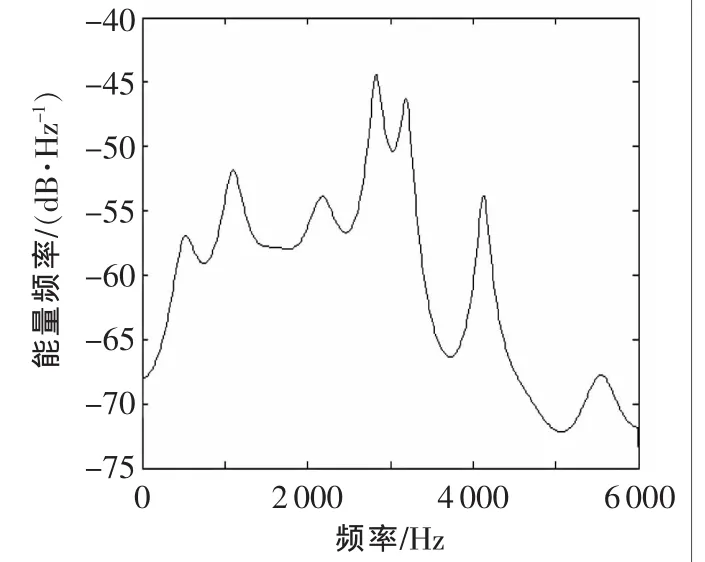
▲图3 故障振动信号的Burg功率谱
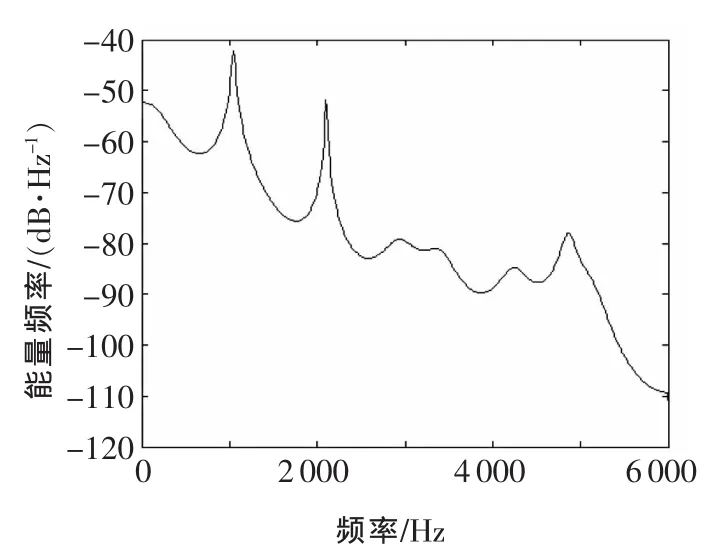
▲图4 正常振动信号的Burg功率谱
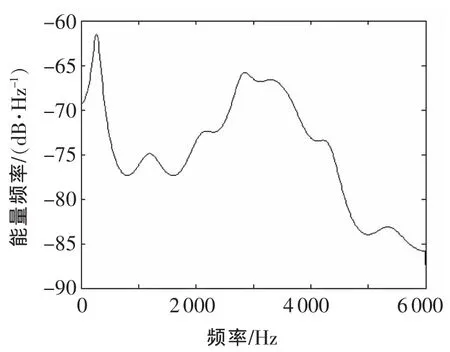
▲图5 小波去噪后的故障振动信号Burg功率谱
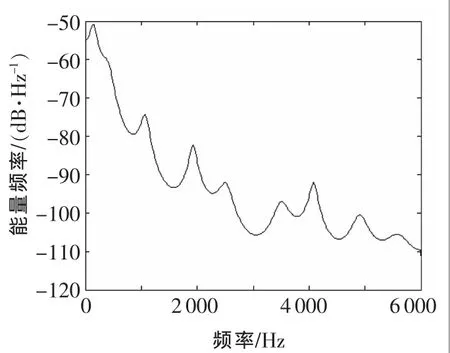
▲图6 小波去噪后的正常振动信号Burg功率谱
为此可以采用对振动信号进行小波分析处理,去除噪声,提高信噪比,再对去噪后的振动信号进行Burg功率谱分析,通过分析振动信号的功率谱特征变化情况,找到振动信号的异常变化,就可以确定故障的特征信息。图5为小波去噪后的故障振动信号Burg功率谱,图6为小波去噪后的正常振动信号Burg功率谱,可以看到,振动信号在小波分析去噪之后表现出曲线平滑,峰值明显,更加利于故障诊断。
从图5和图6可以发现,正常振动信号的Burg功率谱和故障振动信号的Burg功率谱整体图像略微有所不同,都呈现出随着频率的增加,幅值逐步下降,即能量与频率比处于一个缓慢平稳的下降过程。其中,正常振动信号的Burg功率谱在小有波动的情况下,保持稳定的下降。而故障振动信号的Burg功率谱则在[1000 Hz,4000 Hz]出现了一个波峰,蕴含了大量的故障振动信息。这些异常的特征幅值变化说明设备确实出现了故障,必须进行必要的故障诊断工作。
4 结论
仿真实验结果表明,在往复式活塞隔膜泵主轴的故障诊断中,基于小波分析与Burg功率谱的故障诊断方法对隔膜泵主轴的故障诊断是有效和可行的。通过小波分析处理,去除噪声,提高信噪比,再对去噪后的振动信号进行Burg功率谱分析,最后研究和分析振动信号的功率谱特征变化情况,能够准确地得出隔膜泵主轴的运行状况。因此,基于小波分析与Burg功率谱的故障诊断对往复式活塞隔膜泵主轴的故障诊断具有重要意义。
[1]印嘉,吴建德,王晓东,等.基于HHT的往复式隔膜泵主轴故障诊断研究[J].传感器与微系统,2013,32(4):5-8.
[2]王磊,刘杰,刘树英.往复式活塞隔膜泵曲轴的动态特性分析[J].机械设计与制造,2010(5):238-239.
[3]江超.大型隔膜泵组故障诊断系统研究[D].沈阳:东北大学,2008.
[4]王龙,沈艳霞,季凌燕.基于小波降噪和EMD方法的风力发电系统齿轮箱故障诊断 [J].江南大学学报 (自然科学版),2012,11(2):159-162.
[5]刘正平,王彦强.基于小波分析的滚动轴承故障诊断[J].煤矿机械,2011,32(8):266-268.
[6]孙晓东,权爱娟,李勇.复杂噪声背景下谐波信号频率估计新方法 [J].吉林大学学报 (工学版),2015,45 (2):653-657.
[7]姚诚,刘广孚,李忠国,等.基于小波系数功率谱的潜油电泵偏磨故障诊断 [J].仪器仪表学报,2011,32(8):1757-1762.
[8]朱习军,隋思涟,张宾,等.MATLAB在信号与图像处理中的应用[M].北京:电子工业出版社,2009.

