基于小波分析的跳车对桥梁的振动影响*

刘习军，相林杰，张素侠，周安琪

(1.天津大学机械工程学院 天津，300072) (2.天津市非线性动力学与混沌控制重点实验室 天津，300072)



基于小波分析的跳车对桥梁的振动影响*

刘习军1,2，相林杰1,2，张素侠1,2，周安琪1,2

(1.天津大学机械工程学院 天津，300072) (2.天津市非线性动力学与混沌控制重点实验室 天津，300072)

为研究在跳车情况下，车辆荷载对桥梁振动的影响，以一双塔斜拉桥模型为研究对象，建立考虑跳车情况的车-桥耦合振动试验系统。采用连续小波变换对主梁振动信号的时频特征及能量分布进行了研究，探讨了不同路面工况下跳车对桥梁的冲击作用，得到了不同部位发生跳车时桥梁振动的响应分布规律，为桥梁设计和安全运营提供了参考依据。

斜拉桥； 跳车； 冲击效应； 小波分析； 模型试验

引 言

随着交通运输事业的飞速发展，车辆载重及运行速度不断提高，车辆荷载对桥梁结构的动力作用显著增加。车辆轮载通常引起桥梁局部振动，一定程度上加剧桥面磨损、混凝土开裂，促使桥面铺装出现局部隆起或坑槽，桥面局部不平度随之大幅度增大。车辆通过局部不平度较大路面时又易发生跳车现象，不仅影响行车舒适度，还会增大对桥梁的冲击作用，加速桥面损坏。

目前，国内外关于车致桥梁振动响应问题的研究主要集中在数值模拟方面[1-4]，关于模型试验[5-6]方面的研究以及桥面局部不平度增大引起的跳车现象及其对桥梁冲击作用的研究较少。周华飞等[7]将高速公路路面凹陷变形假设为Ricker小波函数，采用两自由度车辆模型，分析了由路面变形引起的车辆振动水平。文献[8-9]对桥头引道沉降引起的跳车及其对桥梁的影响进行了研究。刘钰等[10]建立了车辆过桥时桥面不平度引起的跳车情况下的车-桥耦合振动计算模型，讨论了在考虑跳车与不考虑跳车两种情况下车辆对桥梁的冲击作用，但其研究仅限于数值分析。

笔者以一双塔斜拉桥模型为研究对象，建立考虑跳车情况的车-桥耦合振动试验系统，完成车辆对桥梁的动力冲击试验。采用小波分析方法对桥梁振动信号进行了较为深入的分析，为车-桥耦合振动的研究提供了新途径，为桥梁设计及安全运营提供了依据。

1 试验系统

1.1 车桥模型

试验模型包括两部分：桥梁模型和车辆模型。试验中的斜拉桥模型以天津滨海大桥为原型，采用双塔三跨式，两边跨跨径相等。模型全长为1.9 m，结构体系为塔墩固结、塔梁分离的漂浮体系，索塔形式采用钻石形，塔高为0.6 m，斜拉索采用空间倾斜双索面形式，密索扇形布置，单面设32根索，全桥共设64根索。桥面为6 mm厚的有机玻璃板，桥宽为170 mm。该模型动力特性可通过特制索力调整器调整索力以及在主梁截面施加配重来进行调整。斜拉桥实物图如图1所示。

图1 斜拉桥实物图

车辆模型采用遥控小车，通过调整车载质量模拟不同的载重车辆，通过在桥面行驶模拟车辆对桥梁的荷载作用。

1.2 测点布置

试验过程中，沿主梁纵轴线布置5个加速度传感器，分别为桥梁左边跨跨中、中跨的1/4、中跨跨中、中跨的3/4以及右边跨跨中位置。测点方向均为竖直方向。同时，在5个测点对应桥面上方布设应变片，测量桥面的动应变响应。试验框图如图2所示，编号1～5对应测点1～测点5。

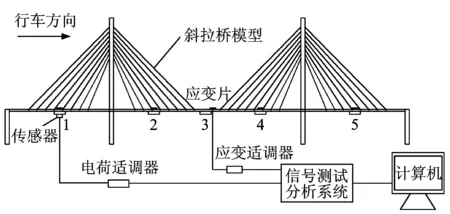
图2 试验框图

2 跳车对桥梁振动的影响

为研究不同路面状况下车辆荷载对桥梁的冲击效应，试验设定6种工况。其中:工况1采用平坦路面;工况2～工况6分别在测点1～测点5对应桥面上布置长为70 mm、宽为5 mm、厚为2 mm的障碍板条来模拟桥面局部不平度增大的情况。试验时，所有工况均采用同一车辆，且保证以相同速度(约1.5 m/s)匀速通过斜拉桥段。

首先运用比利时LMS公司的振动测试分析系统对车辆激励下桥梁模型的振动特性进行了分析，固有频率结果如表1所示。

表1 斜拉桥固有频率测试结果

根据所测得的试验数据，提取各工况各个测点的加速度信号峰值及应变幅值，结果如表2、表3所示。由表中数据可看出，无论是加速度还是动应变信号，有跳车情况下各测点响应均比无跳车情况要大。

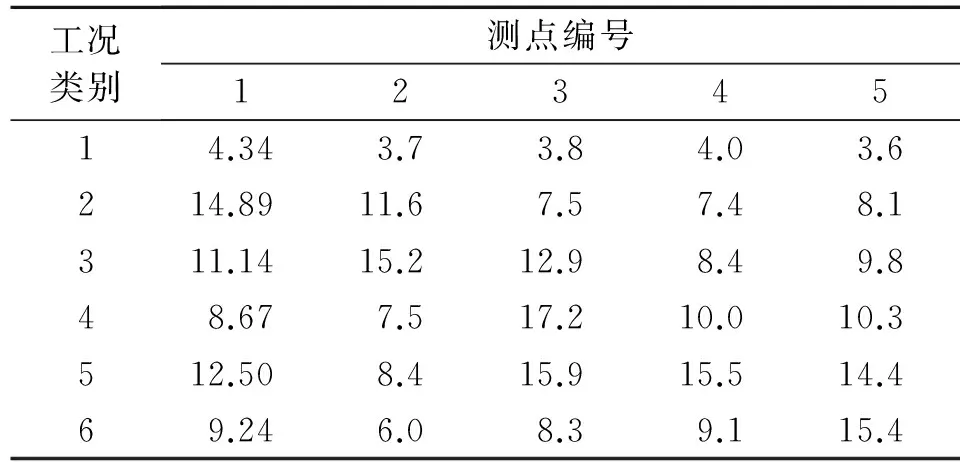
表2 不同工况各测点加速度峰值

表3 不同工况各测点应变幅值

为具体说明这种放大效应，将数据进行进一步处理。所有工况均以工况1为基准，定义结构的动力放大系数[11]为

(1)

加速度信号取加速度峰值，应变信号取应变幅值。计算结果如图3所示。

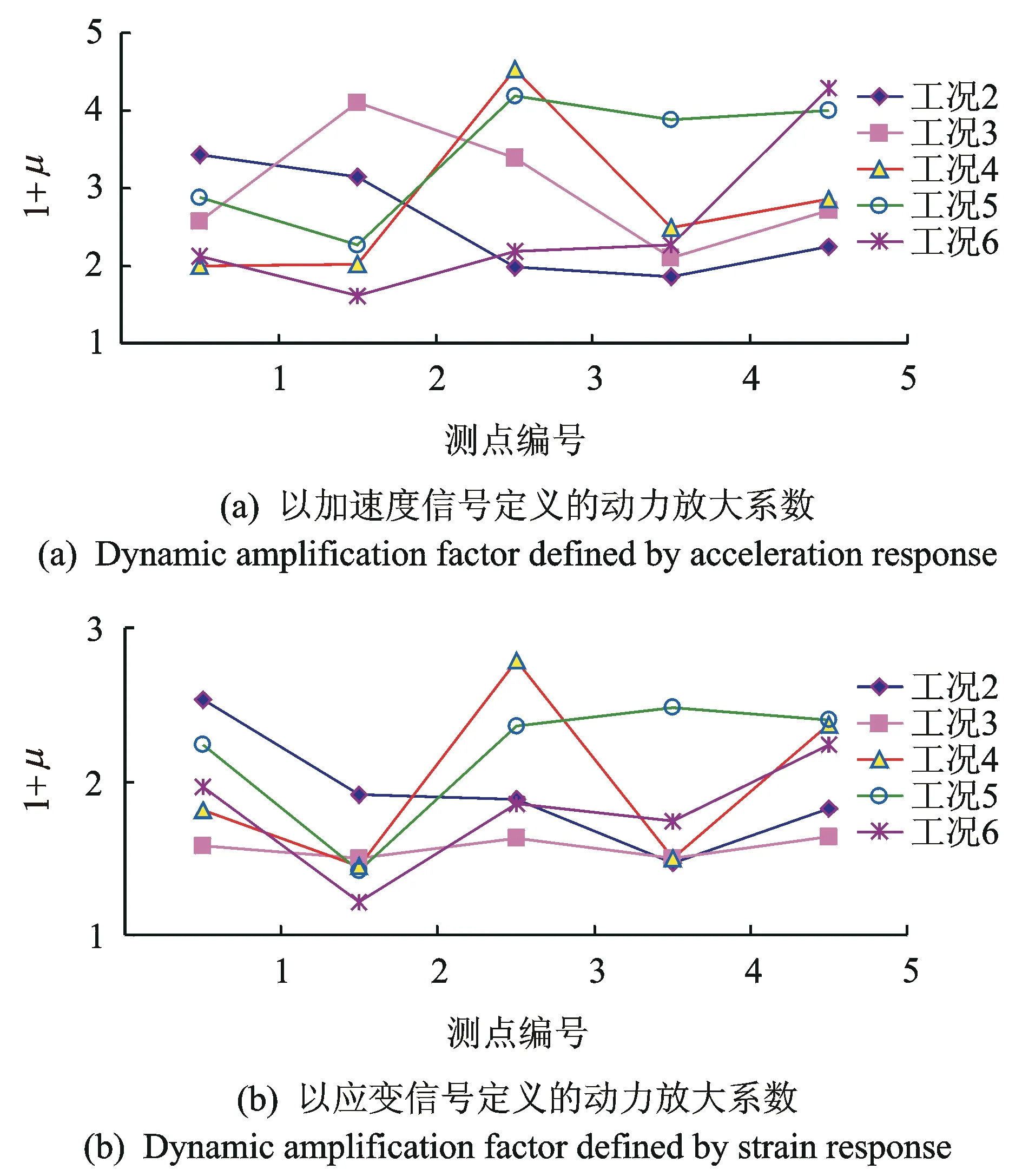
图3 以两种响应量定义的动力放大系数

观察图3，发现以两种响应量定义的动力放大系数变化规律基本一致，主要有以下几点：a.不同工况各测点1+μ值均大于1，进一步证明了跳车对桥梁振动响应的放大效应；b.同一工况不同测点1+μ值不同，表现为跳车位置数值最大，说明跳车对跳车点的局部冲击效应明显大于其他测点；c.两幅图中均为工况4测点3的1+μ值最大，说明中跨跨中桥面局部不平度较大时，车辆荷载对桥梁的局部冲击效应最大。

由以上分析可知，加速度峰值与应变幅值增量的变化规律基本一致，这说明由跳车引起的动态增量主要以低频为主。若为高频分量，两类信号的响应增量变化规律不一定一致。所以，在研究跳车的动态增量时，应以位移信号作为响应量为好，以此为依据才能说明动态增量的增加与桥梁损伤的关系。

3 应用连续小波变换对桥梁振动加速度信号的时频分析

车致桥梁振动是一个动态响应问题，在对其分析时不仅要考虑振动幅值的变化，还应该考虑信号所包含的频率成分、振动持续时间以及信号的能量分布对桥梁结构的影响，为此，应用小波分析的方法对信号进行时频分析。

在采用连续小波变换(continuous wavelet transform,简称CWT)进行时频分析时，选取时频两域局部性能都比较好的Morlet小波[12]。信号f(t)∈L2(R)的CWT定义为

(2)

其中：ψ(t)∈L2(R)为母小波，即Morlet小波；“〈〉”表示内积；“—”表示共轭运算；W(a,b)为小波系数。

小波系数中蕴含着信号在各个尺度a和平移因子b上的信息，通过尺度和平移因子的变化，便可对信号绘制CWT时频图，从而直观地刻画信号的时频特性，反映信号在时频相平面上的状态。同时，对某一尺度a，定义小波功率为

(3)

其中：T为待分析信号时间长度。

由此可知，小波功率反映信号在某一尺度即某一频率关于时间的平均能量分布。

图4 加速度信号时间历程曲线

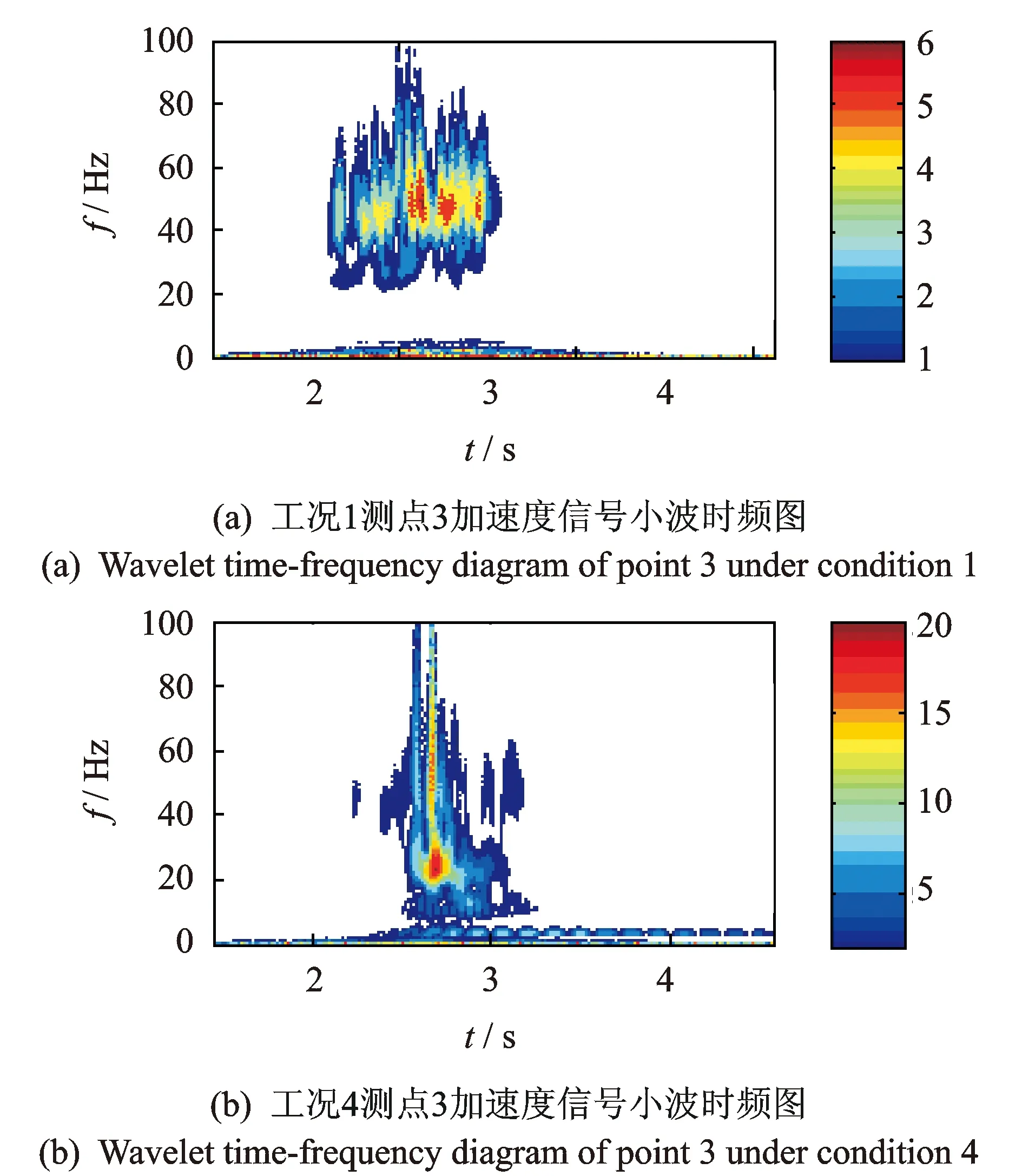
图5 小波时频图

限于篇幅，本节只对工况1和工况4两种工况下测点3的加速度信号进行详细对比分析。图4为两种工况下测点3加速度信号时程曲线，相应的CWT时频图分别如图5(a)和图5(b)所示，图中颜色的浅与深表示小波系数模的大小，小波功率谱图如图6所示。

图6 工况1和工况4测点3加速度信号小波功率谱图

由图5(a)可以发现，无跳车情况时，中跨跨中振动信号所包含的频带范围比较稳定且集中，主要集中在30～70 Hz，包含在该频率范围内的信号持续时间基本相同，此时桥梁结构的振动主要由车辆荷载的持续干扰引起。在图5(b)即中跨跨中发生跳车现象时，信号30 Hz以下频率成分明显增多，高频部分(30～70 Hz)在时间分布上不连续，说明该部分信号不稳定，且从2.5 s这一时刻开始，桥梁以第1阶固有频率频(3.32 Hz)开始衰减振动，跳车对结构瞬态冲击影响起主要作用。图6给出了信号在频域的能量分布状态，在30～100 Hz之间两种工况信号能量分布趋势相同，数值相近；30 Hz以下工况1信号能量几乎为零，而工况4数值很大。由此进一步确定该工况下由跳车引起的信号频率成分约为0～30 Hz。

4 跳车引起的信号成分的提取

由上面分析可知，考虑跳车情况时桥梁振动信号频率成分明显增多，但仅由CWT分析并不能确定具体包含哪些频率成分。本节将采用信号的单子带分解与重构算法以及频谱分析相结合的方法，对跳车引起的信号成分进行有效提取。

单子带信号分解与重构相当于对信号进行滤波，是将原始信号分解到一系列二进划分频带上的过程，各子带信号与原信号具有关系[13]

f(t)=an+dn+dn-1+…+d2+d1

(4)

其中：f(t)为原始信号；a为低频近似部分；d为高频细节部分；n为分解层次。

通过对信号的单子带分解与重构，可以将其定位到任一子带，并可对某些子带信号作特征提取。

图7 各层重构信号及其频谱图

图8 跳车引起的信号小波时频图

图9 跳车引起的信号小波功率谱图

对图4(b)所示的信号采用db40小波基函数进行2层小波分解并进行单子带重构，得到a2，d2和d1这3层信号成分，重构各层信号及其频谱图如图7所示。图7(a)中a2为第2层低频重构信号，频率范围为0～25 Hz。结合上节分析结果，提取a2部分作为工况4测点3由跳车引起信号成分，图8和图9分别为该信号成分的CWT时频图和小波功率谱图。

由图8可见，提取的跳车引起的信号成分其时频特征与图5(b)中0～30 Hz之间的图像特征相吻合。此外，由图7(b)及图9可以看出，工况4测点3由跳车引起的信号的频率成分主要是3.32,10.94以及21.68 Hz，分别与斜拉桥的竖向1阶、3阶及5阶固有频率(见表1)相接近，可见主跨跨中跳车相当于跨中受突加荷载作用，其响应只是对称振型的叠加[14]。

类似地，可得到其他工况跳车冲击点处由于跳车引起的信号成分，结果汇总如表4所示。由表4发现，当跳车冲击点在2，3及4部位时，信号中均叠加了接近3.32 Hz的频率成分，说明在该斜拉桥主跨发生跳车时极易引起结构以第1阶固有频率振动；而冲击点在边跨位置时则易引起较高频振动；2,4位置由于接近第3阶振型节点，在该部位跳车时响应中无第3阶振动成分。由分析可知，无论车辆在何处发生跳车现象，均引起结构以相应各阶固有频率振动，这对桥梁结构的安全是极为不利的。

表4 不同工况下跳车引起的信号成分

5 结 论

1) 考虑跳车情况时，通过结构不同部位加速度响应和动应变响应数据所得到的动力放大系数其变化规律基本一致，主要有以下两点：一是跳车对跳车点的局部冲击效应明显大于其他位置；二是对于该斜拉桥中跨跨中桥面局部不平度较大时，车辆荷载对桥梁的局部冲击效应最大。

2) 小波分析理论可应用于车桥耦合振动研究中，利用小波可对桥梁振动信号进行有效时频分析，并可将跳车引起的信号成分与车辆正常行驶引起的信号成分进行有效分离。进一步的研究结果表明，跳车对桥梁的冲击作用相当于附加荷载作用，将引起结构以低阶振型为主的大幅振动，并且车辆于不同部位发生跳车将引起桥梁不同振型的大幅振动。

3) 路面局部状况恶化将加剧桥面及桥梁的损坏，因此做好桥面保养，定期对桥面进行维护是保证桥梁安全运营的有效手段。

[1] Law S S, Zhu X Q. Bridge dynamic responses due to road surface roughness and braking of vehicle[J]. Journal of Sound and Vibration, 2005,282(3-5):805-830.

[2] Bruno D, Greco F, Lonetti P. Dynamic impact analysis of long span cable-stayed bridges under moving loads[J]. Engineering Structures, 2008,30(4):1160-1177.

[3] Ding Lina, Hao Hong, Zhu Xinqun. Evaluation of dynamic vehicle axle loads on bridges with different surface conditions[J]. Journal of Sound and Vibration, 2009,323(3-5):826-848.

[4] 张鹤，张治成，谢旭，等.月牙形多拱肋钢管混凝土桁架拱桥动力冲击系数研究[J].工程力学，2008，25(7)：118-124.

Zhang He, Zhang Zhicheng, Xie Xu, et al. Theoretical study on the impact factor of crescent-shaped multi-rib concrete filled steel tube truss arch bridges[J]. Engineering Mechanics, 2008,25(7):118-124. (in Chinese)

[5] 卢凯良，张卫国，宓为建，等.运用模态综合法的车桥自激激励耦合振动分析[J].振动、测试与诊断，2012，32(3)：419-425.

Lu Kailiang, Zhang Weiguo, Mi Weijian, et al. Coupled vibration analysis for self-excitation vehicle-bridge based on mode synthesis method[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(3):419-425. (in Chinese)

[6] 张欣，杜修力.桥梁行车激励辨识的实验模态方法[J].振动、测试与诊断，2013，33(3)：364-368.

Zhang Xin, Du Xiuli. Identification of dynamic load on bridges due to traffic[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(3):364-368. (in Chinese)

[7] 周华飞，蒋建群，张土乔，等.高速公路路面凹陷变形引起的车辆振动水平分析[J].振动与冲击，2004，23(2)：55-57.

Zhou Huafei, Jiang Jianqun, Zhang Tuqiao, et al. Vehicle′s vibration level induced by pavement depression of free way[J]. Journal of Vibration and Shock, 2004,23(2):55-57. (in Chinese)

[8] 张丽芳，艾军.桥头引道沉降对简支梁冲击效应的影响分析[J].振动与冲击，2009，28(10)：4-7.

Zhang Lifang, Ai Jun. Impact influence of a bridge approach differential settlement on a simply supported bridge[J]. Journal of Vibration and Shock, 2009,28(10):4-7. (in Chinese)

[9] 丁勇，谢旭，Ou Francis T K，等.基于分布式弹簧-阻尼单元的桥头跳车动力荷载分析[J].土木工程学报，2012，45(12)：127-135.

Ding Yong, Xie Xu, Ou Francis T K, et al. Analysis of dynamic load of vehicle bumping at bridge-head using distributed spring-damper element[J]. China Civil Engineering Journal, 2012,45(12):127-135. (in Chinese)

[10]刘钰，范晨光，高芳清，等.考虑跳车情况下的车-桥耦合振动研究[J].四川大学学报:工程科学版，2012，44(S2)：141-145.

Liu Yu, Fan Chenguang, Gao Fangqing, et al. Analysis of vehicle-bridge coupling vibration under the condition of considering the vehicle pitching[J]. Journal of Sichuan University: Engineering Science Edition, 2012,44(S2):141-145. (in Chinese)

[11]杨建荣.车-桥耦合作用下公路桥梁局部振动研究[D].上海:同济大学，2007.

[12]曹茂森，任青文，邱秀梅，等.基于Morlet小波时间尺度表示的地下连续墙无损检测[J].石油大学学报，2004，28(3)：100-105.

Cao Maosen, Ren Qingwen, Qiu Xiumei, et al. Nondestructive detection method for underground continuous wall using time-scale representation of Morlet wavelet[J]. Journal of the University of Petroleum, China, 2004,28(3):100-105. (in Chinese)

[13]杨建国.小波分析及其工程应用[M].北京：机械工业出版社，2005:35-70.

[14]刘习军，贾启芬.工程振动理论与测试技术[M].北京:高等教育出版社，2004:236-241.

10.16450/j.cnki.issn.1004-6801.2015.06.019

*国家自然科学基金资助项目(51009107)；天津市基础重点基金资助项目(13JCZDJC27100)；天津市青年基金资助项目(13JCQNJC04200)

2013-12-09；

2014-03-18

U441.3; TH113

刘习军，男，1956年2月生，教授、博士生导师。主要研究方向为非线性振动理论及应用、桥梁振动力学及损伤动力检测。曾发表《MR-TMD减振系统对连续箱梁桥振动控制研究》(《振动与冲击》2012年第31卷第20期)等论文。 E-mail：lxijun@tju.edu.cn