同步压缩小波与希尔伯特-黄变换性能对比*

熊 炘，占 锐，王小静

(上海大学机电工程与自动化学院 上海，200072)



同步压缩小波与希尔伯特-黄变换性能对比*

熊 炘，占 锐，王小静

(上海大学机电工程与自动化学院 上海，200072)

经验模式分解(empirical mode decomposition 简称EMD)中包络均值代替信号实际均值的算法误差，使其在处理复杂多频振动信号时易出现模式混叠，引起分析误差。针对这一问题，采用同步压缩小波变换(synchrosqueezed wavelet transform ，简称SWT)根据时间-尺度平面中各元素模的大小，对平面内的能量进行重新分配，通过映射关系将时间-尺度平面转化为时间-频率平面，获得频率曲线更加集中的时频表达。这一方法的正交性与算法自身良好的数据驱动性降低了模式混叠引起的时频分析误差，多组分仿真信号时频特征提取证明了SWT的优异时频特性，利用旋转机械不对中振动位移信号进行了实测数据分析。结果表明，SWT能够精确描述谐波信号的频率构成，且所获时频能量分布集中，时、频域定位精度高，为机械设备的状态监测与故障诊断提供了一种新的时频分析手段。

时频分析； 同步压缩小波变换； 希尔伯特-黄变换； 特征提取； 旋转机械

引 言

时频分析可洞察信号各组分的结构，直观反映出信号中频率构成随时间的变化规律，在设备状态监测与故障诊断领域越来越受到重视[1]。近年来，一系列新的时频分析工具的出现为快速精确提取时频特征提供了新的途径。第2代小波分析、多小波分析[2]以及基于经验模式分解的希尔伯特-黄变换(Hilbert-Huang transform, 简称HHT)被广泛应用于工程实际中的各个领域[3]。

与传统的基于内积运算与波形匹配的方法不同，HHT是一种创新性的时频分析工具[4]，包括两个基本步骤：经验模式分解(EMD)和希尔伯特变换(Hilbert transform，简称HT)。EMD是一种数据驱动的自适应的筛选算法，将时间序列信号分解为一组基本模式分量(intrinsic mode function, 简称IMF)。IMF理论上为窄带分量，但在实际应用中发现EMD所分解的IMF并非全为窄带信号，各组分之间并不严格正交。这种单一IMF中含有截然不同的信号成分或者同一频率成分被分解到不同的IMF中的现象，称之为模式混叠[5],其与信号的间歇现象以及不能准确提取极值点有关[6]。

针对EMD模式混叠问题，一些学者提出了改进方法。文献[7-8]对高斯白噪声的统计特性进行了研究，发现EMD是一种有效的数字滤波器，为总体经验模式分解(ensemble empirical mode decomposition，简称EEMD)的提出奠定了基础。实践表明,EEMD在一定程度上抑制了模式混叠的产生[9]，但同时丧失了EMD的完备性以及完全数据驱动性的优点，并且计算量大。在EEMD的基础上,Torres等[10]提出了噪声自适应的完备性总体平均经验模式分解(complete ensemble empirical mode decomposition with adaptive noise，简称CEEMDAN)，它保留了EMD的完备性以及自适应性，并且计算量为EEMD的一半，在实际应用中极大改善了非平稳信号的分解效果。EEMD 和CEEMDAN是两种典型的EMD新算法，被广泛应用于机械故障诊断。李昌林等[11]提出了一种EEMD和Laplace小波结合的滚动轴承诊断方法。王帮峰等[12]利用EEMD实现飞行数据小突变信号检测。陈隽等[13]利用EEMD实现疲劳应变信号降噪。然而采用包络均值代替数据的实际均值，使得现有EMD改进算法都不可能完全解决模式混叠问题，而且EMD本质上是一种数值算法，很难用严格的数学解析式来解释。

Daubechies等[14]在寻求解释EMD算法原理数学基础的过程中，提出了一种与EMD算法原理近似的新方法——同步压缩小波变换。SWT是一种时频域再分配方法，与第2代小波变换及多小波变换不同，SWT在小波变换的基础上，利用同步压缩方法，根据时间-尺度平面中各元素模的大小，对时间-尺度平面的能量进行重新分配，最后通过特殊的映射将时间-尺度平面转化为时间-频率平面，获得频率曲线更加集中的时频表达。SWT的提出为时频分析提供了新思路，文献[15-16]证明了SWT在有限扰动或白噪声污染情况下有界稳定，并详细论述了SWT的Matlab实现方法。

笔者将SWT理论引入旋转机械振动信号特征提取当中。首先，介绍了SWT的基础算法和步骤；然后，将SWT应用于旋转机械仿真信号的时频特征提取，与HHT时频特征提取结果进行对比分析；最后，利用SWT对实际机组信号进行特征分析，证明其对于旋转机械谐波响应信号特征提取的有效性。

1 同步压缩小波变换

SWT以小波变换为基础，采用同步压缩的方法提取小波脊线，使谐波信号的时频表达效果更加清晰，主要包括以下几个步骤。

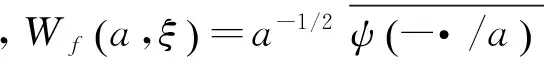
(1)

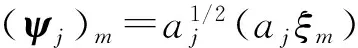
2) 相变换。连续小波变换的相变换为

(2)

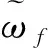
(3)

离散小波相变换为

(4)

Wf的偏导数通过下式计算

(5)

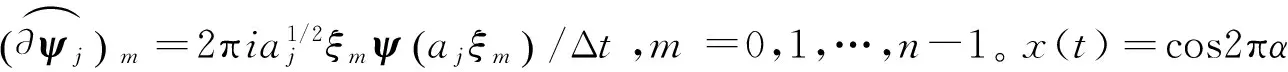
3) 同步压缩得到Tf(w,b)。定义f的离散同步压缩小波变换为

(6)

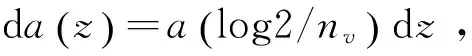
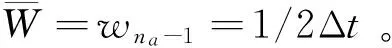
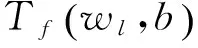
forl=0 tona-1；

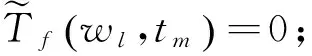
end for

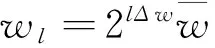
其中

{将规范化后的变量代入积分中：ΔZ=1}

end for

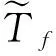
(7)

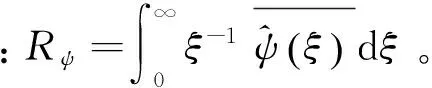
2 仿真信号分析

旋转机械因其振动机制所产生的振动响应通常为一组谐波信号的叠加，对于此类信号的特征提取，在时频面上准确描述频率和能量随时间的变化至关重要。下面利用一组模拟的调频调幅信号，对CEEMDAN和SWT时频分析方法进行比较分析。

采用的模拟信号具有5个组分，S1～S5主频分别为40，120，250，500和700 Hz，除主频以外S2包含20 Hz的调频成分，S3包含15 Hz的调幅成分。

对各组分信号直接进行HHT，得到0～1 s内的时频图如图1所示，由于各组分满足IMF的条件，并且有效地避免了模式混叠，得到理想的时频图，作为参照。

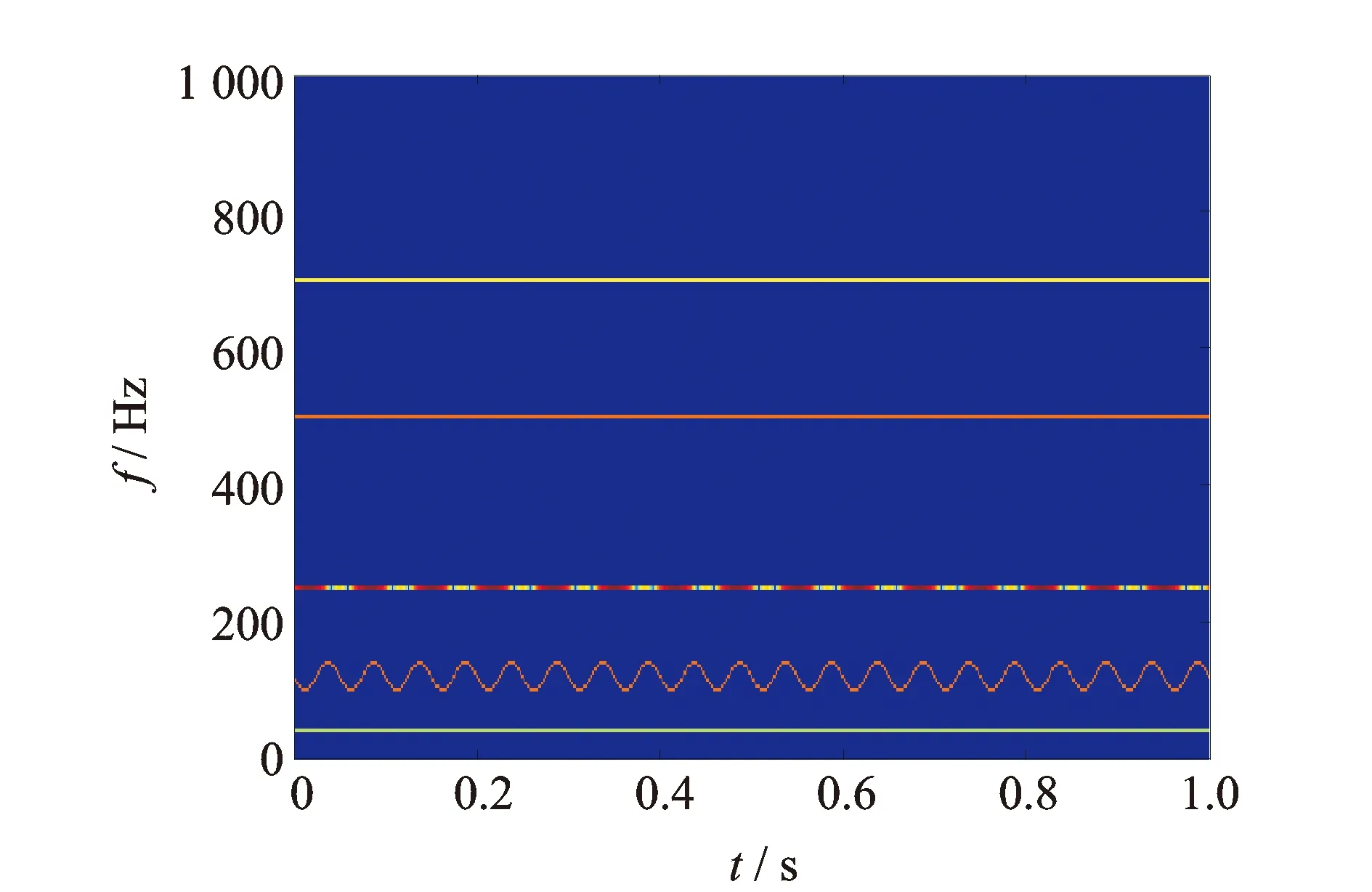
图1 各组分分别进行HHT所得时频图

采用CEEMDAN对仿真信号进行分解，文献[10]选择迭代次数Ι为100，ε为0.2，所得的时频图如图2(a)所示。采用SWT仿真信号进行分解，选择Morlet小波作为基本小波，nv取32，所得时频图如图2(b)所示。

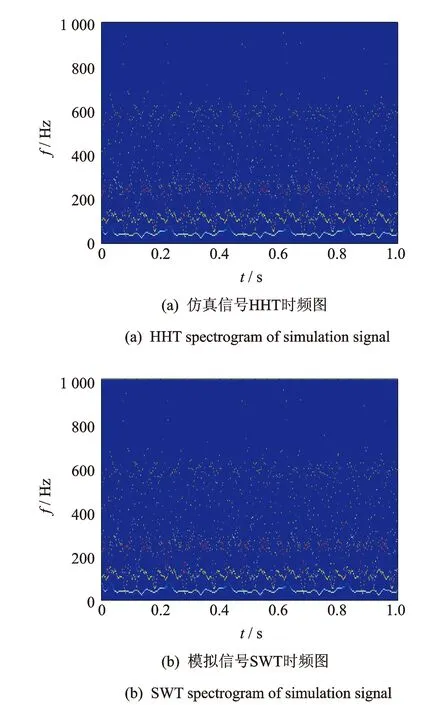
图2 模拟信号时频分布

图2(a)与图1对比结果表明，HHT时频图相比于理想时频图，其频率分布广泛，高频部分出现明显的频率发散现象，低频部分出现虚假的调频波动，从中只能分辨出3个频率成分。

图2(b)与图1对比结果表明，SWT时频图与理想时频图具有相同的频率分布，各频率成分相互独立，无虚假成分产生，从图中可清晰读出40，120，250，500和700 Hz。120 Hz处有20个振荡波形，表明其调频频率约为20 Hz；250 Hz处明暗变化15次，表明其调幅频率约为15 Hz，这些特征都与仿真信号相吻合。为了提高计算速度，小波尺度采用指数尺度序列，因此同步压缩时频图的纵坐标为指数坐标。

为分析两种方法分解的正交性，给出分解后的前6阶IMF的时域波形及其频谱，如图3所示。由FFT频谱图可看出，CEEMDAN并没有完全消除模式混叠，前2阶IMF频率混淆严重。IMF1具有250，500和700 Hz的频率成分，其频带分布较宽，不具备窄带特征，故对其进行希尔伯特变换求瞬时频率不具物理意义，导致时频图上出现虚假频率。

对SWT分解的组分进行分析，选择分解的层数为5，对其进行FFT变换。图4所示SWT中C1～C5分别对应原始信号中的S4，S3，S1，S2和S5，精确还原了原始信号的组成成分。分析结果表明，SWT相比于HHT正交性更好，SWT各组分频率相对独立，无虚假频率产生，且具有良好自适应性，对复杂多组分的谐波信号具有理想的分解效果。

3 转子故障特征提取案例分析

为进一步验证SWT的工程实用性，利用转子不对中位移信号进行时频特征提取，并与HHT特征提取性能进行对比。转子不对中是旋转机械常见的故障，常伴随径向振动中较大的2倍频振动能量，频谱以1，2倍频成分为主。不对中越严重，2倍频所占比例就越大，并且可能出现高次谐波。

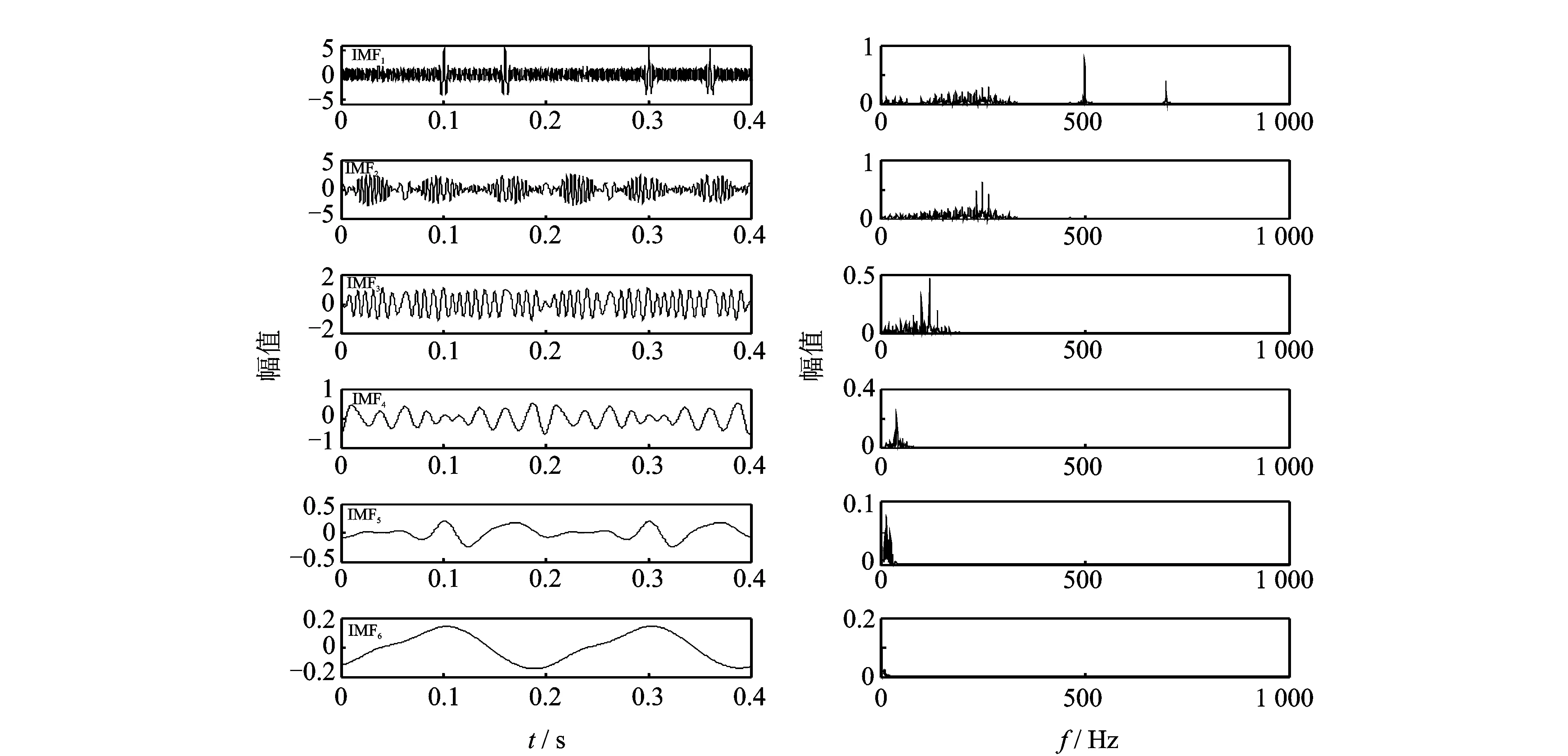
图3 仿真信号IMF及其频谱

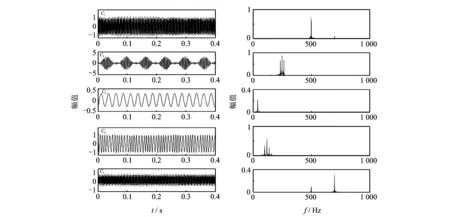
图4 SWT分解成分与频谱

实际振动信号来自某炼油厂烟机，结构如图5所示，额定转速为12 kr/min，传感器安装于联轴器两侧，升速到11 130 r/min时进行测量，采样频率为2 kHz，信号样本长为0.5 s。信号时域波形如图6(a)所示，FFT变换的幅值谱如图6(b)所示。

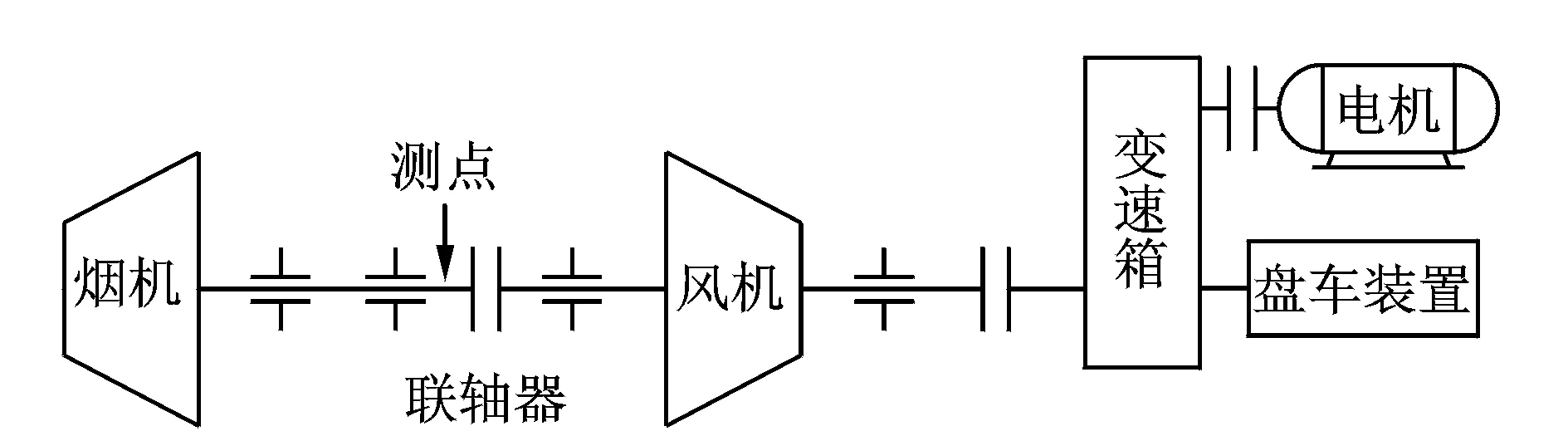
图5 烟机简图

从图6(b)中可发现，故障信号的频率呈连续分布，其中较为突出的频率成分约为48,185,373,558,746和931 Hz，分别对应1/4倍频、1倍频、2倍频、3倍频和4倍频。

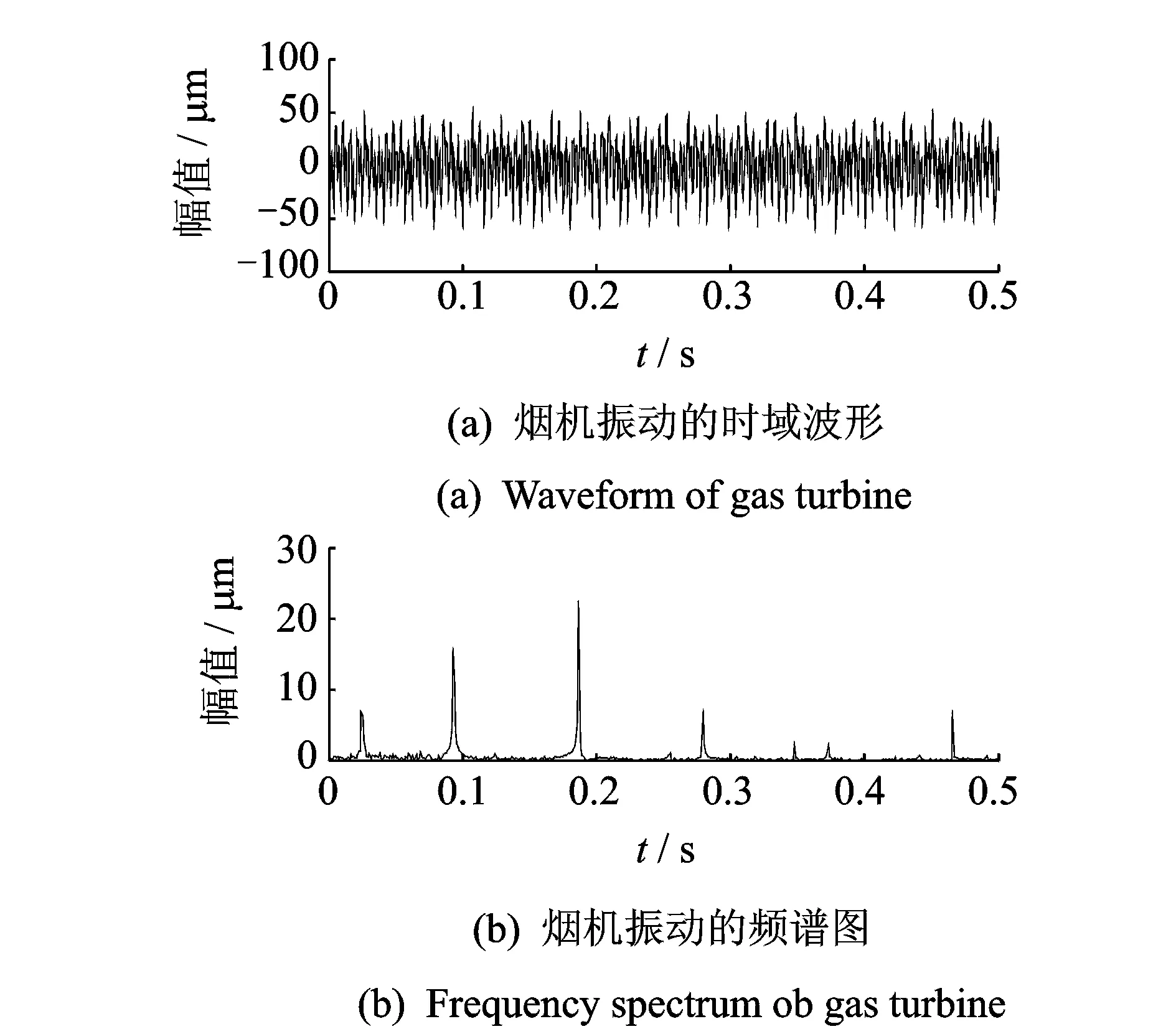
图6 烟机不对中振动信号

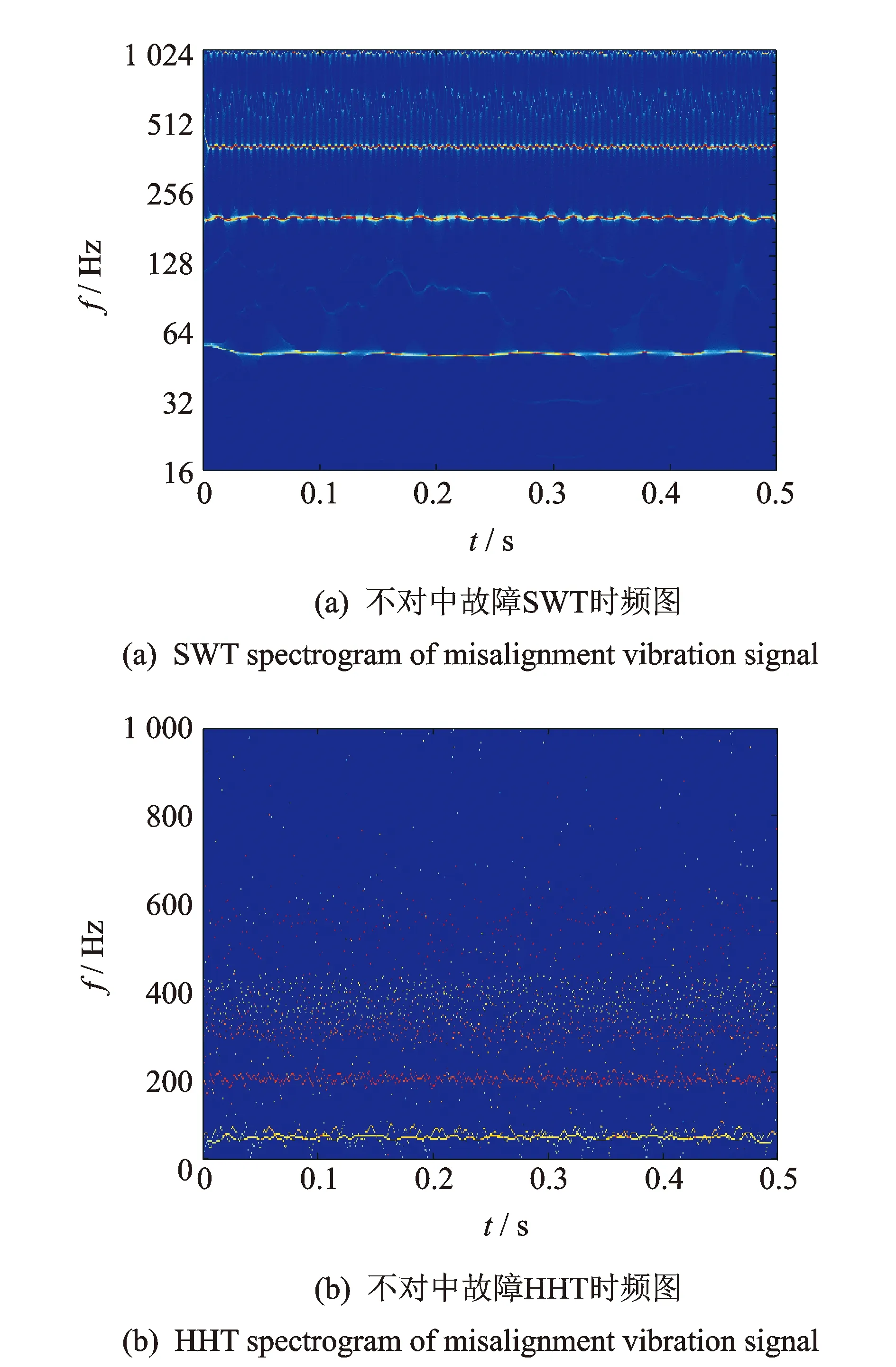
图7 不对中振动信号时频图

用SWT对不对中振动信号进行时频特征提取，选择Morlet小波作为基本小波，nv设为64，所得时频图如图7(a)所示。用HHT进行时频特征提取，选择CEEMDAN分解信号，添加白噪声为0.3，迭代次数设为500，最大筛选次数为5 000，所得时频图如图7(b)所示。

对比图7中的两幅时频图可见，HHT与SWT在一定程度上都能反映出机器振动的频率成分，图7(a)中的SWT时频图能够清晰描述1/4倍频、1倍频和2倍频；3倍频能量虽较小，但仍可分辨出；4倍频位于时频图的最上方，谱线也清晰可见。图7(b)的HHT时频图中，只能分辨出1倍频和1/4倍频，高频部分谱线发散严重，发生了严重的模式混叠。对比结果表明，SWT的时频图更准确地还原了原始信号成分，除在实际频率附近有细微模糊外，其他区域无虚假成分，其时频提取精度更高，并且抗噪性能更好。

进一步研究对实际信号的分解效果，得出每个组分的时域波形及其频谱。SWT分解组分及其频谱如图8(a)所示，CEEMDAN分解的组分及其频谱如图8(b)所示。从图中可清楚看出，SWT对实际信号的分解效果明显优于HHT。图8(a)中的C1～C6各频带相对独立，频率集中，表明其分解效果理想。图8(b)中IMF1～IMF6相互之间有明显的频率重叠，相同频率被分解到不同组分中，不满足窄带条件。

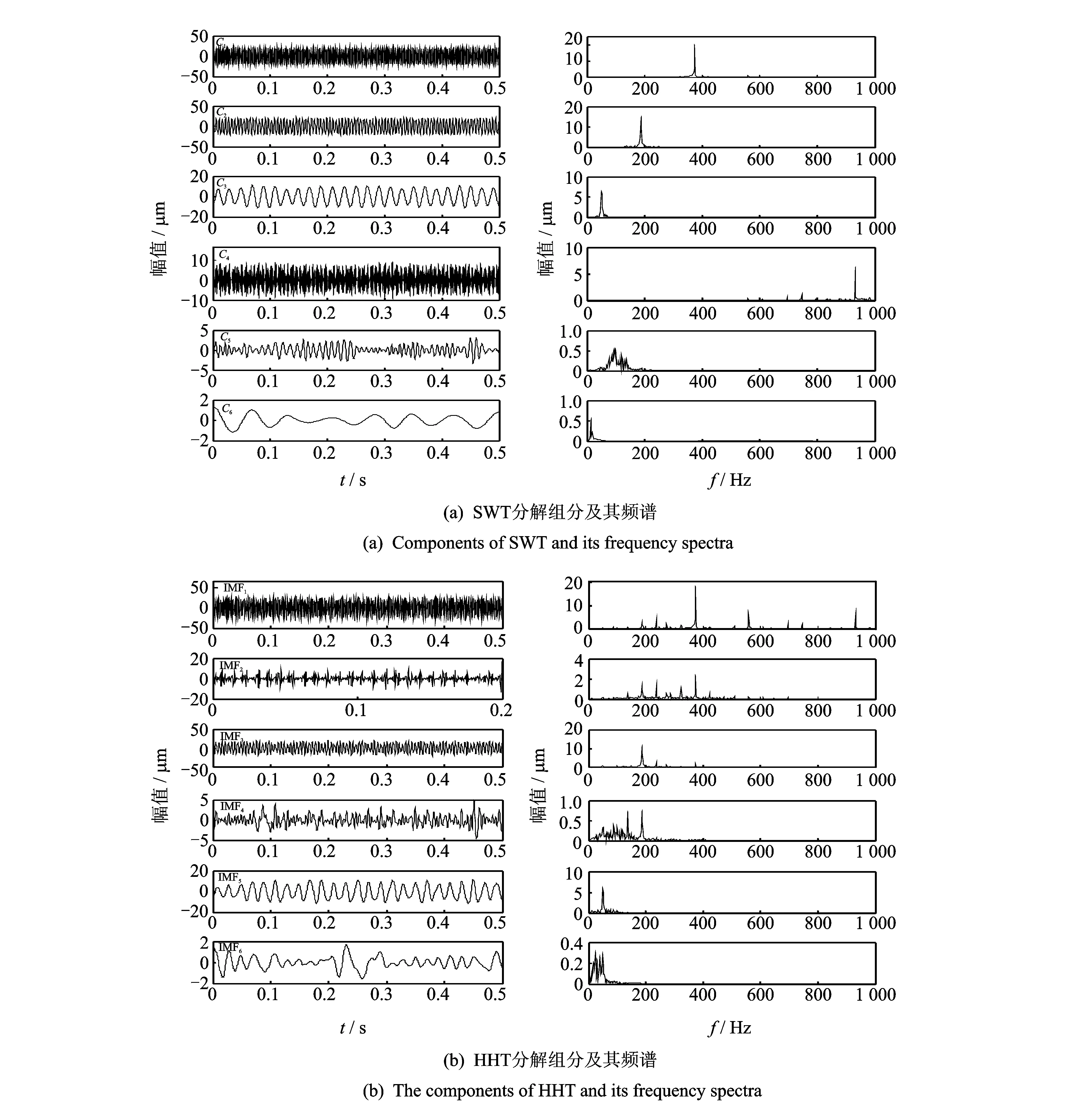
图8 不对中振动信号分解组分

4 结 论

1) 通过对仿真信号分析表明，SWT所得时频图更加清晰地反映出频率随时间的变化规律，时频图上谱线相对集中并且无虚假频率产生。对各分解组分的分析发现，SWT分解后的各组分均为窄带信号，并且频率分布相互独立，具有良好的正交性，精确还原了原始多频谐波信号的组成。HHT所得的时频图无法避免模式混叠，所得IMF并不全为窄带信号，尤其是1阶IMF包含多个频率成分，与其他组分频带相互重叠，导致时频图上出现虚假频率成分。

2) 在实测故障信号分析中，SWT所得的时频图能够清晰反映出不对中故障的谐波频率成分，通过时频图谱线颜色的变化规律，可准确表达信号的能量分布，且时频定位准确，辅助确诊了烟机不对中故障。

[1] 何正嘉, 陈进, 王太勇, 等. 机械故障诊断理论及其应用[M].北京: 高等教育出版社, 2010:1-12.

[2] Yan Ruqiang, Gao R X, Chen Xuefeng. Wavelets for fault diagnosis of rotary machines: a review with applications[J]. Signal Processing:Part A, 2014, 96: 1-15.

[3] Lei Yaguo, Lin Jing, He Zhengjia, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical Systems and Signal Processing, 2013, 35(2): 108-126.

[4] Huang N E, Shen Zheng, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998，454(1971): 903-995.

[5] 胡爱军, 孙敬敬, 向玲.经验模式分解中的模态混叠问题[J]. 振动、测试与诊断, 2011, 31(4): 429-434.

Hu Aijun, Sun Jingjing, Xiang Ling. Mode mixing in empirical mode decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(4): 429-434. (in Chinese)

[6] Peng Zhike, Tse P W, Chu Fulei. A comparison study of improved Hilbert-Huang transform and wavelet transform: application to fault diagnosis for rolling bearing[J]. Mechanical System and Signal Processing, 2005, 19(5): 974-988.

[7] Flandrin P, Rilling G, Goncalves P. Empirical mode decomposition as a filter bank[J]. Signal Processing Letters, IEEE, 2004, 11(2): 112-114.

[8] Wu Zhaohua, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 2004, 460(2046): 1597-1611.

[9] Wu Zhaohua, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[10]Torres M E,Colominas M A, Schlotthauer G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]∥ IEEE International Conference on Acoustic Speech and Signal Processing. Prague：[s.n.]，2011：4144-4147.

[11]李昌林, 孔凡让, 黄伟国.基于EEMD和Laplace小波

的滚动轴承故障诊断[J]. 振动与冲击, 2014, 33(3): 63-69.

Li Changlin, Kong Fanrang, Huang Weiguo. Rolling bearing fault diagnosis based on EEMD and Laplace wavelet[J]. Journal of Vibration and Shock, 2014, 33(3): 63-69. (in Chinese)

[12]王帮峰, 林剑祥, 芦吉云. 基于EEMD-HT的飞行数据小突变信号检测[J]. 振动、测试与诊断, 2013, 33(3):388-392.

Wang Bangfeng, Lin Jianxiang, Lu Jiyun. Small mutation signal detection for flight data based on empirical mode decomposition and Hilbert transform[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3): 388-392. (in Chinese)

[13]陈隽, 李想. 运用总体经验模式分解的疲劳信号降噪方法[J].振动、测试与诊断, 2011, 31(1): 15-19.

Chen Jun, Li Xiang. Application of ensemble empirical mode decomposition to noise reduction of fatigue signal[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(1): 15-19. (in Chinese)

[14]Daubechies I, Lu Jianfeng, Wu H T. Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261.

[15]Thakur G, Brevdo E, Fukar N S, et al. The Synchrosqueezing algorithm for time-varying spectral analysis: robustness properties and new paleoclimate applications[J]. Signal Processing, 2013, 93(5): 1079-1094.

[16]Brevdo E. The synchrosqueezing toolbox[EB/OL]. [2014-08-20]. http://web. math.princeton.edu/～ebrevdo/synsq/

10.16450/j.cnki.issn.1004-6801.2015.06.016

*国家自然科学基金资助项目(50876057);上海大学理工类创新基金资助项目(K.10-0109-13-007);上海市高校青年教师培养计划资助项目(N.37-0109-14-203)

2014-09-15；

2014-10-24

TN911．7; TH165．3

熊炘，男，1983年11月生，工学博士、讲师。主要研究方向为机电装备故障诊断、机械动力学和智能检测技术。曾发表《A new procedure for extracting fault feature of multi-frequency signal from rotating machinery》(《Mechanical Systems and Signal Processing》2012,Vol.32)等论文。

E-mail: xiongxinme@gmail.com