基于能量分布的机床整机动态特性优化方法*

邓聪颖，殷国富，肖 红，孟昭渝溪

(1.四川大学制造科学与工程学院 成都，610065) (2.成都普瑞斯数控机床有限公司 成都，611731)



基于能量分布的机床整机动态特性优化方法*

邓聪颖1，殷国富1，肖 红2，孟昭渝溪1

(1.四川大学制造科学与工程学院 成都，610065) (2.成都普瑞斯数控机床有限公司 成都，611731)

基于机床结构中的能量分布，在准确建立立式加工中心整机有限元模型的基础上提出一种整机动态性能优化方法。采用弹簧阻尼系统等效结合部的接触特性，基于辨识的结合部等效刚度和阻尼值在Ansys中建立了立式加工中心整机有限元模型，对整机进行模态分析和谐响应分析。通过整机模态试验验证了该有限元模型的准确性，并根据有限元分析与试验结果确定整机的薄弱模态。计算薄弱模态下整机、结合部的弹性能以及结合部在整机中的弹性能分布率，以分布率较高的结合部作为薄弱结合部。基于薄弱结合部的等效接触刚度提出优化方案，优化后薄弱结合部的弹性能分布率明显降低，主轴轴端的动态响应幅值降低，从而使整机动态性能得到改善，验证了该优化方法的可行性。

能量分布； 结合部； 立式加工中心整机； 动态特性； 有限元分析

引 言

随着机床加工性能的不断提高，对机床动态性能的要求也越来越高。机床是由许多零部件按特定的要求结合起来的，其结合面的阻尼、刚度分别占整机阻尼和刚度的90%和60%以上[1]；因此，为准确地对立式加工中心进行整机动态特性分析，须基于结合部建立准确的动力学模型。Zhang等[1]应用均质梁、集中质量及结合部单元对机床进行整机动态建模，基于结合面的动态基础特性参数，应用子结构建立了整机系统的动力学方程，对整机动态性能进行了预测。Mao等[2]基于频响函数矩阵和动刚度矩阵的互逆关系，采用动态测试数据辨识了机床固定结合部动态参数，为准确地建立机床动力学模型奠定了理论基础。李玲等[3]采用子结构综合法建立了结合部动力学模型，基于修正已知模型的思想，通过频响函数辨识了重型龙门数控机床结合部的等效刚度和阻尼参数。吴文镜等[4]应用状态矢量传递思想对刚体、柔体和结合面三类元件进行整合，得到用一个高维矩阵表示的整机模型，求解该高维矩阵即可得到整机的动态特性。张宇等[5]采用等效弹簧阻尼器模拟结合面特性，基于机械阻抗综合法推导出一种直接利用结构实测频响函数识别机床结合部参数的方法。王禹林等[6]应用吉村允孝法确定结合部参数，采用弹簧阻尼单元模拟结合面接触特性，基于结合面对大型螺纹磨床整机进行静动态特性优化。

笔者采用弹簧阻尼单元模拟机床各主要结合面间的接触特性，基于辨识的结合面刚度阻尼值在Ansys中建立了立式加工中心整机有限元模型，并对其进行模态分析和谐响应分析，通过整机锤击法模态试验验证了该模型的准确性。在准确建立整机有限元模型的基础上，基于机床结构中的能量分布提出一种整机动态性能优化方法。通过计算整机薄弱模态下各结合部与整机的弹性能，得到各结合部的弹性能在整机弹性能中的分布率。针对弹性能分布率较高的薄弱结合部进行优化分析，基于其结合面等效接触刚度提出优化方案，避免了对整机所有结合部进行讨论的盲目性。优化后薄弱结合部的弹性能分布率明显降低，主轴轴端的动态响应幅值降低，机床振动得到很好的抑制。

1 立式加工中心有限元模型的建立

1.1 立式加工中心几何模型的简化

建立合理的动力学模型是机床动态特性分析的基础，笔者研究对象为四川某机床厂的某型立式钻铣加工中心。其主要由床身、床鞍、工作台、立柱、主轴箱、主轴六大功能部件组成。按照以下原则对机床进行合理的简化[6]：

1) 在真实反映结构特征的基础上，忽略倒角、小孔及螺纹等小特征；

2) 对不改变装配位置的凸台、定位孔及工艺孔等简化或忽略；

3) 对结构中小锥度、小曲率曲面进行直线化和平面化；

4) 根据立式加工中心真实结构，将刀库、电机配置柜简化为质量块。

简化后的整机模型如图1所示。

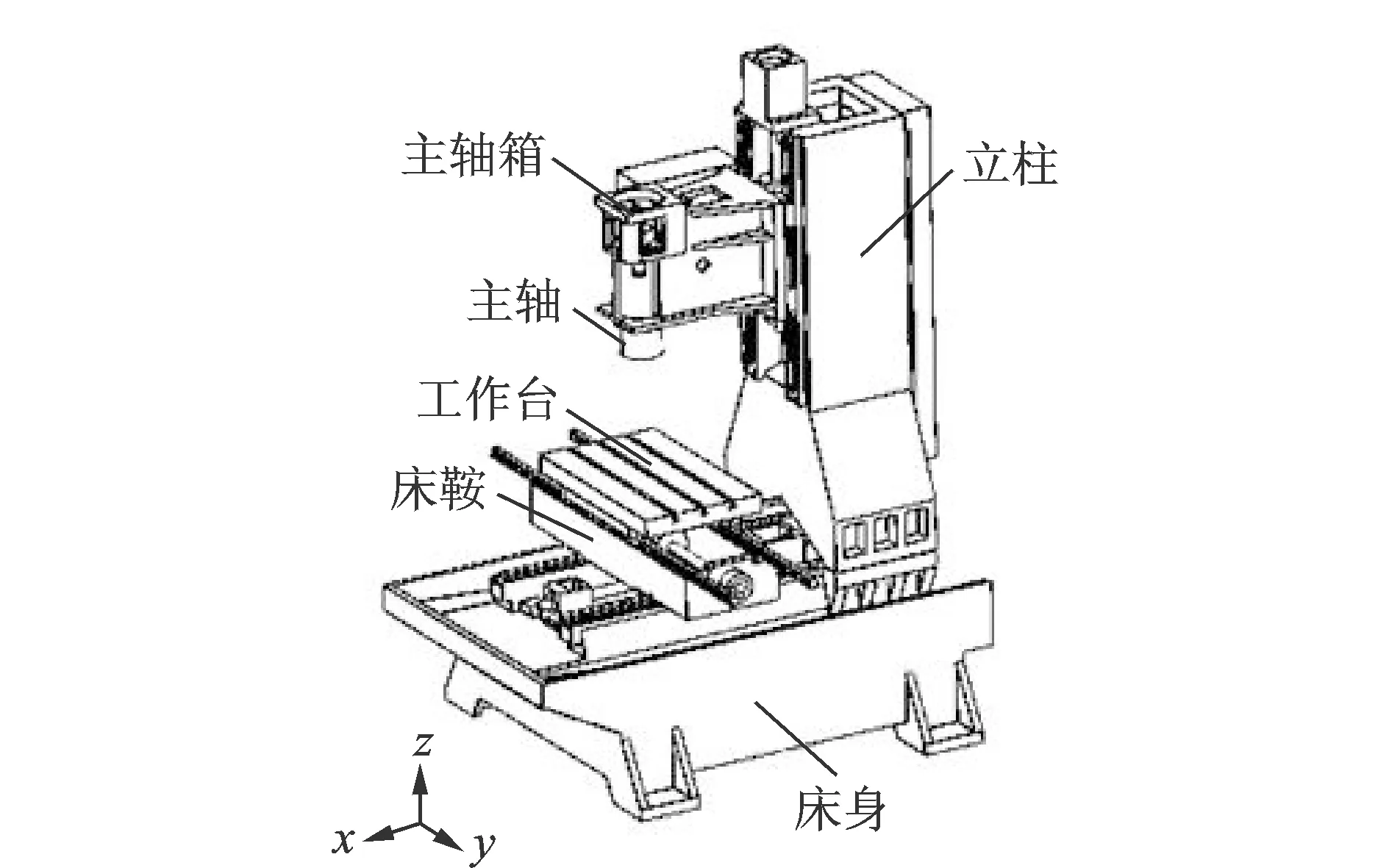
图1 立式加工中心整机简化模型

1.2 立式加工中心整机动力学模型的建立

结合部的阻尼、刚度分别占整机阻尼和刚度的90%和60%以上，在建立整机动力学模型时，必须融入结合部特性。结合部表现出既能存储能量又能消耗能量，因此将结合面接触特性等效为弹簧-阻尼系统。笔者对立式加工中心固定结合部、滑动结合部及滚动结合部的等效接触刚度和阻尼系数进行了参数辨识。

1.2.1 导轨滑块结合部

基于模态参数，利用优化思想对导轨结合部的等效接触刚度和阻尼系数进行了有效的辨识。滑块与导轨由合金钢制成，其弹性模量为206 GPa，密度为7 800 kg/m3，泊松比为0.3。采用六面体单元对滑块与导轨进行网格划分，共建立4 560个单元、5 901个节点。忽略滚动体的质量，用弹簧阻尼单元模拟滑块与导轨结合面间的接触特性。滑块总长为72 mm，以图2中面A为基准，每隔24 mm建立一组弹簧阻尼单元，均匀布置在滑块前、中、后3个截面上。每个截面共分布4个弹簧阻尼单元，其位置根据滑块滚珠和导轨接触形式分别垂直于导轨滑块并与水平方向成45°夹角，等效动力学模型如图2所示。

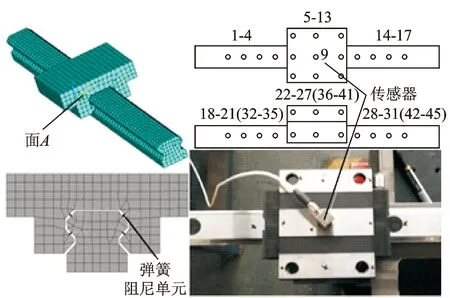
图2 导轨滑块动力学模型与试验测点布置

采用LMS公司的LMS系统进行数据采集及模态参数分析。试验采用多点激励、单点响应的测量方式，共布置45个激励点，加速度传感器安装在图2所示的点9处。点9既为响应拾取点，也为激励点。在9点进行激励时，激振力锤尽量靠近它。

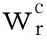
1) 以固有频率计算值和试验值建立式(1)所示的目标函数，求取结合面接触刚度k

(1)

2) 以阻尼比的计算值和试验值建立式(2)所示的目标函数，求取结合面阻尼系数c

(2)

(3) 在Matlab中编写能与Ansys实现交互运算的优化控制程序。Matlab自动调用Ansys，并将等效接触刚度和阻尼系数迭代初值传递给Ansys。Ansys分析完毕后，通过APDL命令将结果反馈到Matlab循环控制程序中，以此流程自动迭代直至达到要求的收敛条件。

比较结合部前4阶固有频率和阻尼比，识别的滑块导轨结合面等效接触刚度和接触阻尼系数分别为5.83×108N/m，5 143 (N·s)/m。表1和表2分别为固有频率、阻尼比试验值和仿真值的比较结果，表中固有频率的误差在5%以内，阻尼比的误差在4.5%以内，表明建立的有限元模型较为准确地反映了导轨滑块结合部的动力学特性。

表1 结合部固有频率试验值和仿真值对比

Tab.1 Comparison of predicted and experimental frequencies

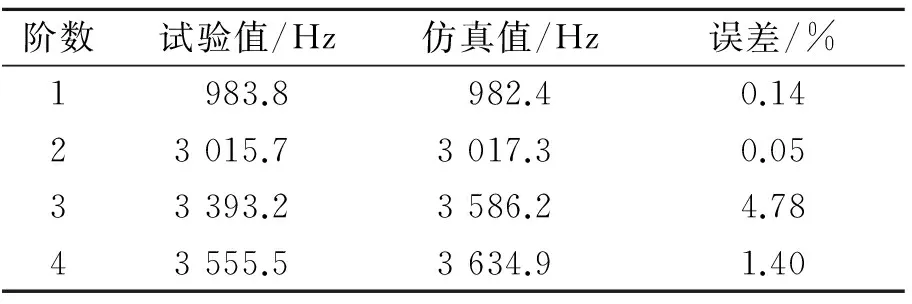
阶数试验值/Hz仿真值/Hz误差/%1983.8982.40.1423015.73017.30.0533393.23586.24.7843555.53634.91.40

表2 结合部阻尼比试验值和仿真值对比

Tab.2 Comparison of predicted and experimental damping ratio

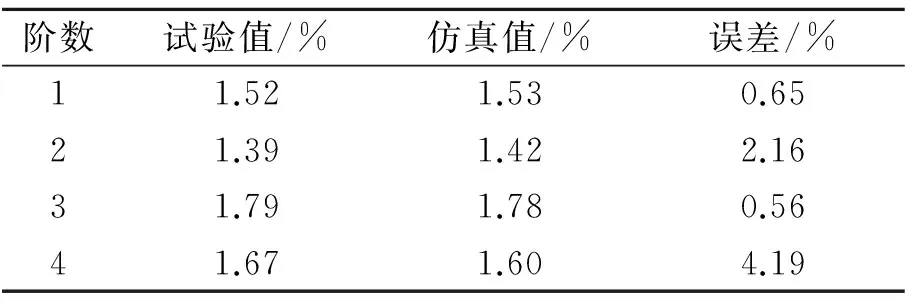
阶数试验值/%仿真值/%误差/%11.521.530.6521.391.422.1631.791.780.5641.671.604.19

1.2.2 固定结合部

本研究中固定结合部主要针对立式加工中心的螺栓联接，其结合面间弹簧阻尼单元的分布由螺栓的数目、螺栓的型号以及结合面面积决定。根据吉村允孝法,结合面的等效接触刚度和阻尼系数可以通过对单位面积结合面的刚度和阻尼求积分来获得,其计算公式[8]如下

(3)

(4)

(5)

(6)

其中：pn为结合面的面压；kn(pn)，kt(pn)，cn(pn)，ct(pn)分别为结合面单位接触面积的法向、切向等效接触刚度和阻尼系数；Kn，Kt，Cn，Ct分别为结合面法向、切向等效接触刚度和阻尼系数。

螺栓结合部动力学参数主要与结合面材料、结合面间介质、加工方法、加工质量及法向面压等有关，其中螺栓结合面面压P[9]可由式(7)、式(8)获得

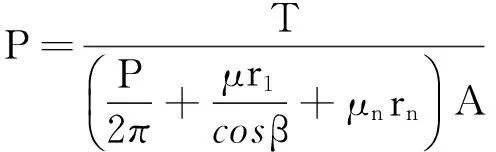
(7)

(8)

其中：T为预紧力矩；μ为螺旋副摩擦因数；μn为六角螺母支撑面摩擦因数；P为螺距；r1为螺纹孔半径；rn为六角螺母圆环面的当量摩擦半径；D0为螺纹孔中径；D1为六角螺母直径。

根据式(7)、式(8)计算螺栓结合面面压，通过文献[10]查取结合部法向、切向单位接触面积的等效刚度和阻尼系数，再根据式(3)～式(6)计算结合面各方向的等效接触刚度和阻尼系数。以立式加工中心关键固定结合部床身-立柱螺栓结合部为例，结合面材料为铸铁，粗糙度为1.6μm,计算得到结合面面压为5.04 MPa，并计算得到表3所示的结合面等效接触刚度和阻尼系数。图3为螺栓结合部动力学模型，圆圈处表示立柱-床身结合面间弹簧阻尼单元接触点的位置。根据结合面尺寸，共均匀布置如图3所示的15个接触点。每对接触点共建立3个弹簧阻尼单元，分别表示法向和两个切向刚度阻尼。

表3 床身-立柱结合面基本参数

Tab.3 Basic parameters of the bed-column joint

方向单位接触面积结合部等效刚度/(N·m-3)阻尼/((N·s)·m-3)刚度/(N·m-3)阻尼/((N·s)·m-3)法向1.67×10133.9×1074.6×10101.1×106切向2.50×10114.2×1066.9×1091.1×105

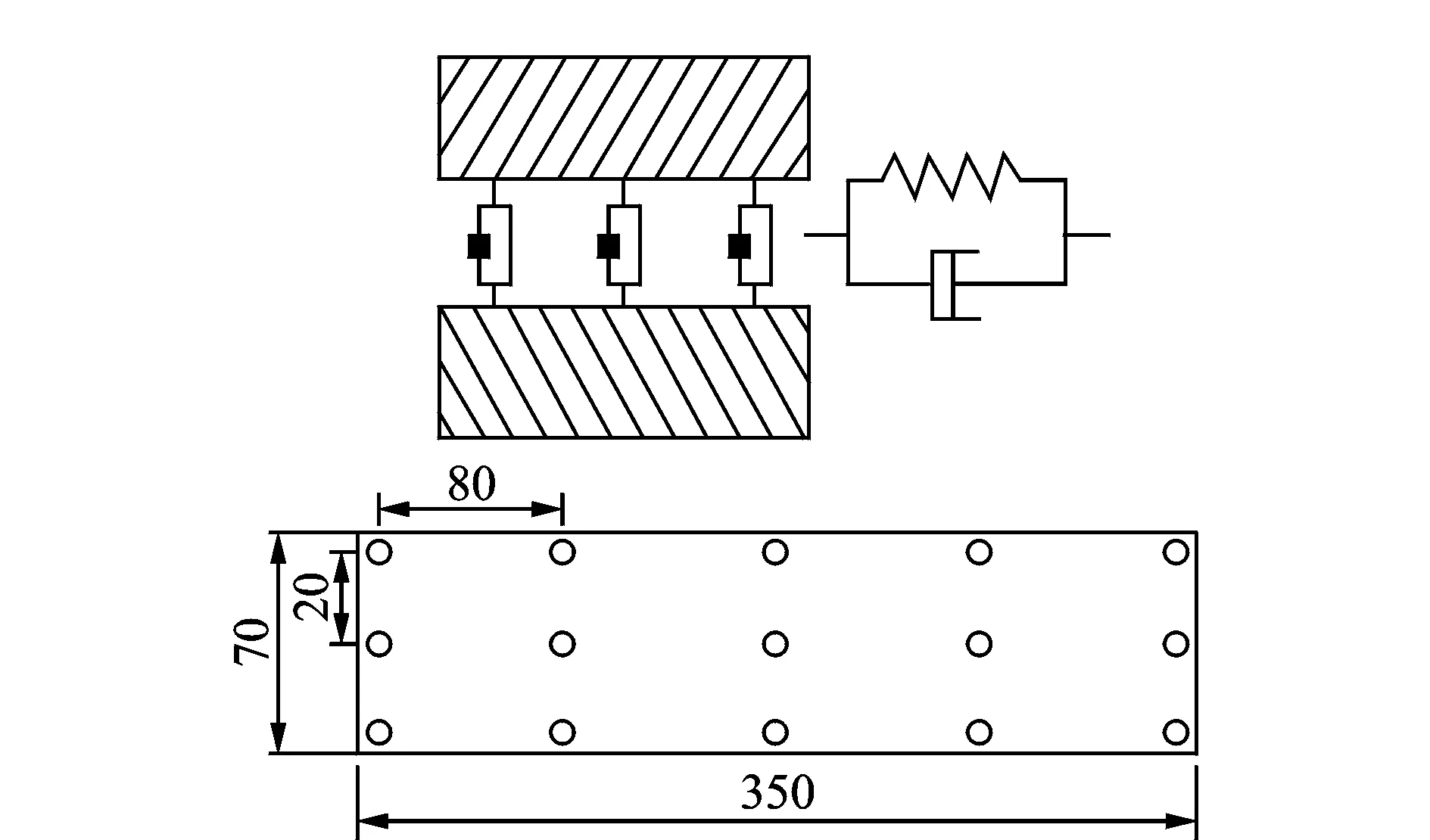
图3 螺栓结合部等效动力学模型(单位：mm)

1.2.3 滚动结合部

本研究中滚动结合部主要包括立式加工中心z向主轴轴承结合部以及x，y，z向的滚珠丝杠结合部。将主轴轴承结合面特性等效为弹簧阻尼单元，轴向与径向分别采用4个均匀分布的弹簧阻尼单元模拟，其轴承刚度可由相应的产品样本获得，图4为其等效动力学模型。

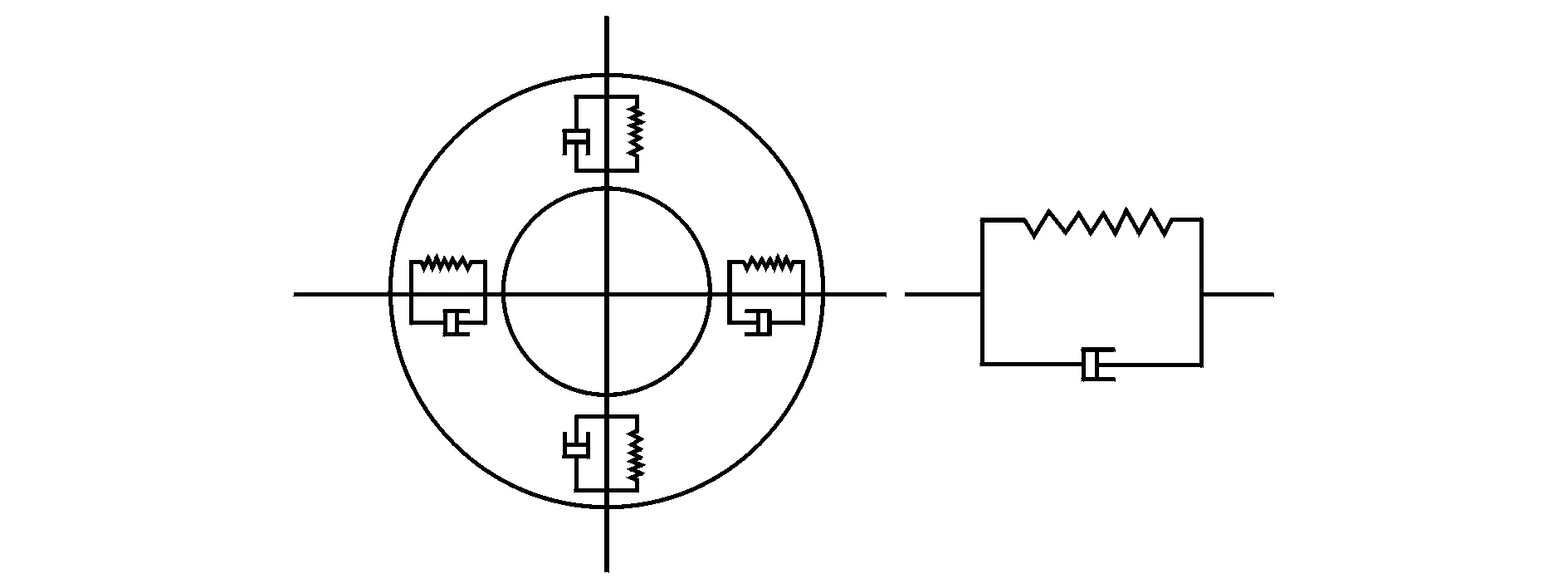
图4 主轴轴承结合部等效动力学模型

滚珠丝杠结合部考虑其轴向接触刚度，图5为其结合部的动力学模型[11]。

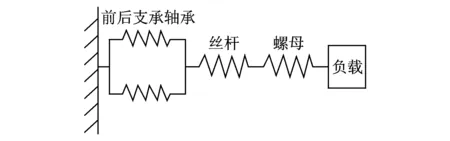
图5 滚珠丝杠结合部动力学模型

根据滚珠丝杠产品手册提供的滚珠丝杠结合部刚性计算式(9)～式(11)，可得结合部轴向等效刚度

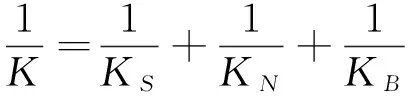
(9)

(10)

(11)

其中：K为滚珠丝杠结合部等效轴向刚度；KS为丝杆轴向刚度；KN为螺帽轴向刚度；KB为支承轴承的轴向刚度；K1为产品手册上提供的刚度值；A为丝杆轴横截面积；L为安装间距；X为负荷作用点间距；Fa为轴向负荷；Ca为基本动额定负荷；E为弹性模量，其值为206 GPa。

支承轴承轴向刚度KB可由相应产品样品获得。通过式(9)～式(11)计算得到表4所示的立式加工中心x，y，z向滚珠丝杠结合部的轴向接触刚度。

表4 滚珠丝杠结合部轴向接触刚度

Tab.4 Axial stiffness of the ball screw N/m

轴向KKSKNKBx2.58×1081.03×1092.60×1081.47×109y2.42×1080.83×1092.45×1081.47×109z1.42×1081.20×1091.43×1081.47×109

1.3 立式加工中心整机动力学模型

将立式加工中心各结合部的动力学特性融入到整机动力学模型中，基于结合面接触特性建立图6所示的整机动力学模型。

图6 整机有限元模型及边界约束

对整机动态性能影响较小的结合部，在有限元软件中采用粘接处理。基础件床身、床鞍、工作台、立柱和主轴箱材料为HT250，其弹性模量为130 GPa，密度为7 300 kg/m3，泊松比为0.25。主轴、直线导轨和滚珠丝杠材料为钢，其弹性模量为206 GPa，密度为7 800 kg/m3，泊松比为0.3。采用Solid45单元对立式加工中心共划分724 537个单元，共采用28个Matrix27和144个Combin14弹簧阻尼单元模拟结合面接触特性。

2 立式加工中心动态特性分析

机床动态特性分析，主要是获得机床各阶固有频率、各阶模态振型以及相关点的动柔度频响函数。通过对获得的数据进行分析，找出机床结构的薄弱环节，从而对机床进行改进设计。笔者针对立式加工中心进行了整机模态分析和谐响应分析。

2.1 立式加工中心整机模态分析

对床身底部施加图6所示的固定约束，约束其6个方向的自由度。在有限元软件中仅求解整机前40阶模态，得到前40阶固有频率和模态振型。在所关心频率0～600 Hz内，立式加工中心主轴系统表现出明显的振动，对应的固有频率和模态振型如表5所示。

除振动明显的主轴系统外，整机振动还表现为：

1) 立柱主要表现在第2，3阶的上下、左右摆动，与立柱-床身间结合面接触刚度有关；

2) 工作台、床鞍主要表现为绕z轴的扭转和y轴的转动，与导轨滑块结合面的接触刚度有关；

3) 床身振动比较微弱。

综合模态分析结果，立式加工中心的薄弱环节为主轴系统。主轴系统中主轴轴端的振动主要由主轴箱的上下摆动、扭转以及主轴自身的弯曲引起。主轴箱除前2阶因立柱摆动外，其余摆动和扭转主要与主轴箱-立柱间导轨滑块结合面、滚珠丝杠结合部的接触刚度有关。主轴的弯曲主要与主轴轴承结合部的动态特性参数有关。

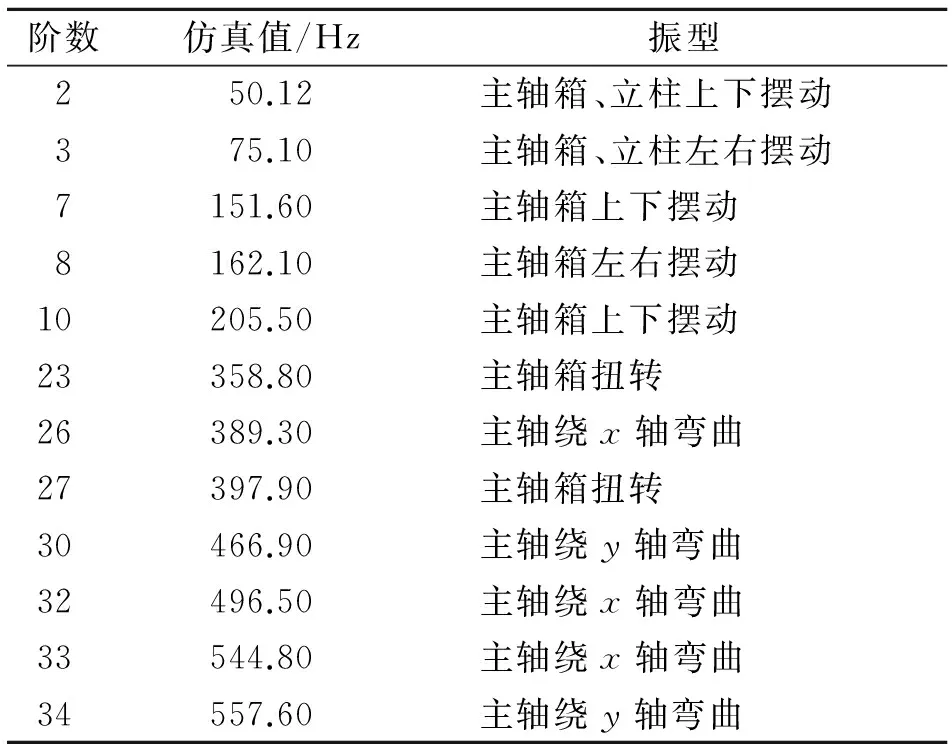
表5 立式加工中心整机固有频率与振型

2.2 立式加工中心整机谐响应分析

模态分析只得到整机的各阶振型，要研究立式加工中心在动态激励下的抗振性，还需对整机进行谐响应分析。主轴轴端的频响函数是抗振性的重要指标，也是识别机床无颤振切削的基础数据[12]，因此，在立式加工中心整机谐响应分析中研究主轴轴端的频响函数。

根据立式加工中心常用转速范围以及刀齿数,主要关心0～600 Hz频率范围内的动力响应。在主轴轴端沿x,y,z向分别施加幅值为1、激振频率为0～600 Hz的简谐力，施加方式见图7，在a，b，c三处按对应的方向分别施加简谐力。图8为主轴轴端x,y,z三向的加速度幅频响应曲线，其中标注“仿真”的为仿真分析结果。

图7 锤击法模态试验

2.3 立式加工中心模型验证

为验证整机有限元模型的准确性，基于LMS振动噪声测试系统，对立式加工中心整机进行锤击法模态试验，获取主轴轴端原点频响函数(frequency response function，简称FRF)。试验采用力锤激振，通过ICP型加速度传感器拾取振动信号，通过LMS系统进行信号处理得到主轴轴端的原点频响函数。图7为现场试验图，图中a，b，c三处放置加速度传感器，分别拾取y,z,x向响应。为获取主轴轴端原点频率响应函数，在a,b,c处激振时应使力锤尽量靠近a,b,c点，试验测得的原点频率响应函数曲线如图8所示，其中标注“试验”的为试验结果。

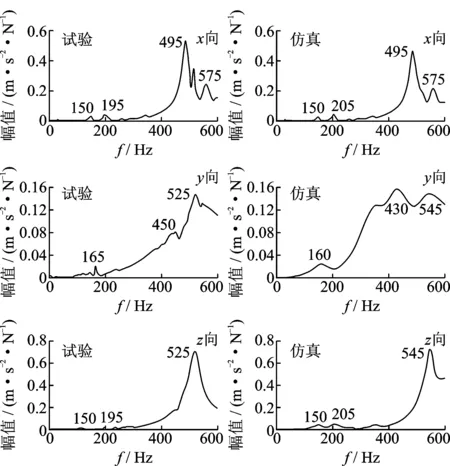
图8 主轴轴端加速度频率响应曲线

比较图8中x,y,z向的频响函数曲线，试验结果和仿真结果变化趋势相近，波峰值频率对应较好，验证了该有限元模型的准确性，为后续整机动态性能预测和结构优化设计奠定了基础。幅值吻合程度相对较低，主要是阻尼研究尚未成熟，对立式加工中心的阻尼模拟精度相对较低。

3 基于能量分布的整机动态性能优化

基于能量分布对整机动态性能优化是指分析机床在各阶模态振动时各种能量(惯性能、弹性能及阻尼能)在整个结构中的分布情况，判定需要进行优化的具体部位。笔者针对结合面的等效接触刚度进行讨论分析，故仅考虑弹性能在整机中的分布情况。

假设系统有N个模块，则N个模块的能量之和为系统能量[12]，系统第s个模块在r阶模态振动时，则模块s与系统的弹性能可定义为

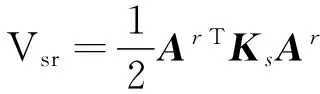
(12)

(13)

其中：Vsr，VAr分别为系统以第r阶模态振动时模块s与系统的弹性能；Ar为系统以第r阶模态振动时模块s所有自由度的幅值向量；ArT为Ar的转置矩阵；Ks为模块s的刚度矩阵。

系统中模块s的弹性能分布率Rs定义为

Rs=Vsr/VAr

(14)

由弹性能分布率可直观地看出机床在各阶模态振动时弹性能在整个结构中的分布情况。分布率越高，表明该结合部刚度越低，应朝着提高该结合部刚度的方向改进设计[12]。

整机模态分析振型结果显示除主轴系统外，其余零部件的振型也主要由结合部引起。因此，基于结合部对立式加工中心整机进行优化设计是可行的。在重点关注的0～600 Hz内，整机中主轴系统相对薄弱，因此，笔者基于机床结构中的弹性能分布，针对与主轴系统动态性能密切相关的主轴轴承结合部、z向导轨滑块结合部、z向滚珠丝杠结合部以及立柱-床身结合部进行优化分析。

从主轴轴端频响函数曲线可得到波峰值频率，同时结合模态分析结果，可找出整机中较为薄弱的几阶模态。通过式(12)、式(13)计算各阶薄弱模态的结合部与整机的弹性能，通过式(14)得到整机中结合部的弹性能分布率。

根据试验和仿真结果，在0～600 Hz内第2，3，7，8，10，32阶为较薄弱模态。以主轴轴承结合部、z向导轨滑块结合部、z向滚珠丝杠结合部以及立柱-床身结合部为研究对象，计算得到表6所示的薄弱模态的结合部能量分布率。

由表6计算结果可知，低阶模态下z向导轨滑块结合部和立柱-床身结合部的弹性分布率较高，高阶模态下主轴轴承结合部的弹性能分布率较高，z向滚珠丝杠结合部的弹性能分布率相对较低。

结合机床厂家的设计经验和对外购件的选择要求，以弹性能分布率较高的主轴轴承、z向导轨滑块和立柱-床身结合面的等效接触刚度为变量列出表7所示的3组优化方案。将每组方案的结合面等效接触刚度值写入有限元模型中进行计算分析，第3组方案的优化效果最为明显。图9为该组方案下主轴轴端谐响应分析结果，表8列出该组方案下弹性能分布率计算结果，表9列出优化前后固有频率比较结果。

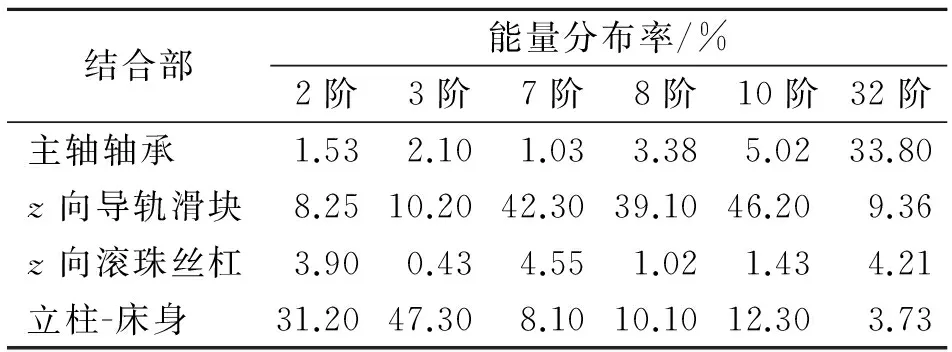
表6 各结合部能量分布率

表7 结合面等效接触刚度取值优化方案

Tab.7 Optimized schemes for the joint stiffness

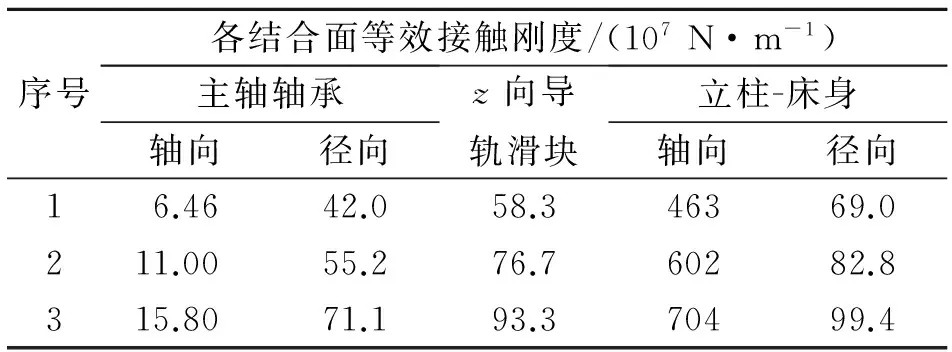
序号各结合面等效接触刚度/(107N·m-1)主轴轴承轴向径向z向导轨滑块立柱-床身轴向径向16.4642.058.346369.0211.0055.276.760282.8315.8071.193.370499.4

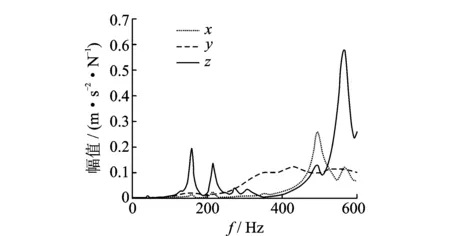
图9 优化后谐响应分析结果

表8 第3组方案分析结果

Tab.8 Results of the third scheme

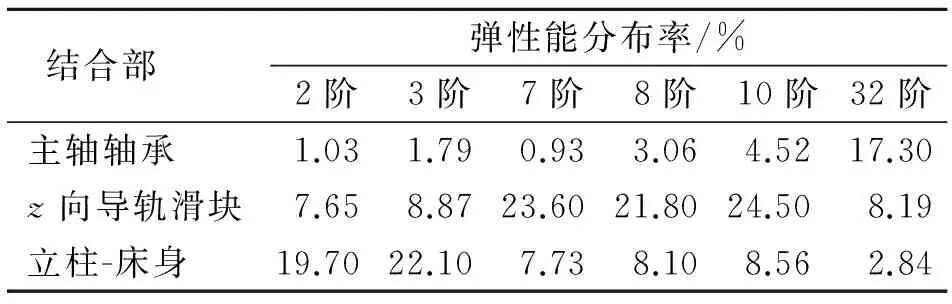
结合部 弹性能分布率/%2阶3阶7阶8阶10阶32阶主轴轴承1.031.790.933.064.5217.30z向导轨滑块7.658.8723.6021.8024.508.19立柱-床身19.7022.107.738.108.562.84

表9 优化后固有频率变化

Tab.9 Frequency results after the optimization

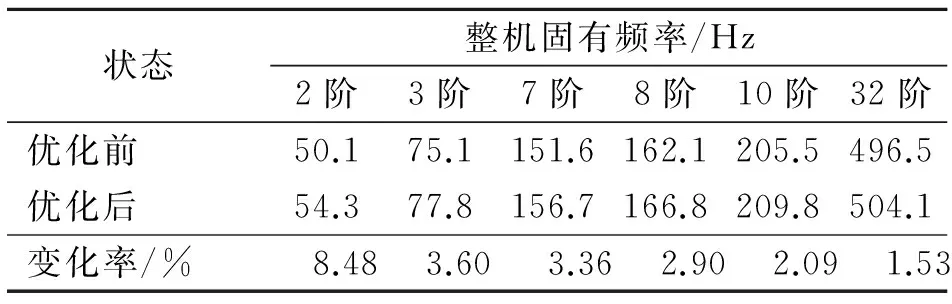
状态整机固有频率/Hz2阶3阶7阶8阶10阶32阶优化前50.175.1151.6162.1205.5496.5优化后54.377.8156.7166.8209.8504.1变化率/%8.483.603.362.902.091.53

比较图9与图7的谐响应分析结果可以看出，优化后x,y,z向主轴轴端的动态响应幅值下降，动态性能明显得到提高。

对比表8和表6可以看出，结合面的等效接触刚度增加后，薄弱模态的结合部弹性能分布率下降较为明显。

从表9可以看出，结合面的等效接触刚度增加后，薄弱模态的固有频率得到提高，其中第2阶固有频率提高达到8.48%。

4 结 论

1) 模态分析显示在0～600 Hz内，整机中主轴系统振动较明显，因此计算主轴-立柱系统中各结合部在薄弱模态振动时的弹性能分布率，确定主轴轴承结合部、z向导轨滑块结合部以及立柱-床身结合部的刚度较差。

2) 针对薄弱结合部，基于其结合面等效接触刚度提出3组优化方案，列出优化效果最明显的方案的分析结果。优化后，薄弱模态的结合部能量分布率明显降低，主轴轴端的动态响应幅值下降，对应的固有频率也得到提高，验证了所提出的基于能量分布对整机动态性能优化的方法是可行的。

[1] Zhang Guangpeng, Huang Yumei, Shi Wenhao, et al. Predicting dynamic behaviors of a whole machine tool structure based on computer-aided engineering[J]. International Journal of Machine Tools & Manufacture, 2003，43(7)：699-706.

[2] Mao Kuanmin，Li Bin，Wu Jun，et al. Stiffness influential factors-based dynamic modeling and its parameter identification method of fixed joints in machine tools[J]. International Journal of Machine Tools and Manufacture，2010，50(2)：156-164.

[3] 李玲，蔡力钢，郭铁能，等.子结构综合法辨识结合部的特征参数[J].振动、测试与诊断，2011，31(4)：439-444.

Li Ling，Cai Ligang，Guo Tieneng，et al. Identification of characteristic parameters of joints by substructures synthesis method[J]．Journal of Vibration，Measurement & Diagnosis，2011，31(4)：399-444. (in Chinese)

[4] 吴文镜，刘强.机床动力学建模的拓展传递矩阵法[J].机械工程学报，2010，46(21)：69-75.

Wu Wenjing，Liu Qiang. Extended transfer matrix method for dynamic modeling of machine tools [J]. Journal of Mechanical Engineering，2010，46(21)：69-75. (in Chinese)

[5] 张宇，廖伯瑜.机床结合部参数的有效识别方法[J].昆明理工大学学报，1998，23(2)：36-41.

Zhang Yu，Liao Boyu. The efficient identification method of joint parameters of machine tools [J]. Journal of Kunming University of Science and Technology，1998，23(2)：36-41. (in Chinese)

[6] 王禹林，吴晓枫，冯虎田.基于结合面的大型螺纹磨床整机静动态特性优化[J].振动与冲击，2012，31(20)：147-152.

Wang Yuling，Wu Xiaofeng，Feng Hutian. Static and dynamic characteristics optimization for a whole large-sized thread grinder based on joint surface [J]. Journal of Vibration and Shock，2012，31(20)：147-152. (in Chinese)

[7] 孙明楠，米良，干静，等. 数控机床导轨结合部动态特性参数优化识别方法研究[J].四川大学学报：工程科学版，2012，44(3)：217-223.

Sun Mingnan，Mi Liang，Gan Jing，et al. An optimum identification method of dynamic characteristic parameters of guideway joint on a NC machine tool[J]. Journal of Sichuan University: Engineering Science Edition，2012，44(3)：217-223. (in Chinese)

[8] 廖伯瑜，周新民，尹志宏.现代机械动力学及其工程应用[M]．北京: 机械工业出版社，2003:261-267.

[9] 米良，殷国富，孙明楠，等.基于结合部动力学特性的立柱-主轴系统动力学模型研究[J].农业机械学报，2011，42(12)：202-207.

Mi Liang，Ying Guofu，Sun Mingnan，et al. Column-spindle system dynamic model based on dynamic characteristics of Joints[J]. Transactions of Chinese Society for Agricultural Machinery，2011，42(12)：202-207. (in Chinese)

[10]张学良.机床结合面动态特性及应用[M].北京:中国科技出版社，2002:55-99.

[11]蒋书运，祝书龙.带滚珠丝杠副的直线导轨结合部动态刚度特性[J].机械工程学报，2010，44(1)：92-99.

Jiang Shuyun，Zhu Shulong. Dynamic characteristic parameters of linear guideway joint with ball screw[J]. Journal of Mechanical Engineering，2010，44(1)：92-99. (in Chinese)

[12]杨櫹，唐恒龄，廖伯瑜.机床动力学[M].北京：机械工业出版社，1983:339-355.

10.16450/j.cnki.issn.1004-6801.2015.06.013

*国家科技重大专项资助项目(2013ZX04005-012)；四川省科技支撑计划资助项目(2012GC0008)

2014-01-09；

2014-03-21

TH113.1； TG659

邓聪颖，女，1991年1月生，博士研究生。主要研究方向为机床动力学、计算机辅助设计与制造。曾发表《基于锥阀的新型井下智能节流系统》(《四川大学学报：工程科学版》2013年第45卷增刊1)等论文。 E-mail：scudcy@163.com