核密度估计法在板件概率损伤识别中的应用*
孙汝杰,陈国平,孙东阳,何 成,周兰伟
(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)(2.重庆大学航空航天学院 重庆,400044)
核密度估计法在板件概率损伤识别中的应用*
孙汝杰1,陈国平1,孙东阳2,何 成1,周兰伟1
(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)(2.重庆大学航空航天学院 重庆,400044)
基于谱元法将核密度估计方法用于解决结构的损伤识别,从而得到了损伤位置的概率密度函数。通过建立压电-结构耦合的三维谱元法模型,模拟Lamb波在铝板完好及损伤结构中的传播过程。利用连续小波变换计算响应信号在传感器之间的飞行时间,得到Lamb波在结构中的传播速度。通过对Rayleigh-Lamb方程的数值分析,得到Lamb波的理论传播速度,并将其与谱元法得到的结果进行对比,证实了谱元法模型的准确性。在椭圆定位技术的基础上,考虑环境不确定性对测量信号的影响,引入核密度估计方法将损伤位置识别转化为一种概率性问题。讨论了3种噪声水平情况下的损伤位置的概率密度函数,并给出了最终识别的结果。结果表明,核密度估计方法能够有效地识别出损伤位置,最大误差在5%左右。
谱元法; Lamb波; 连续小波变换; 核密度估计; 概率损伤识别
1 问题的引出
为了满足航空航天结构的高可靠性和低成本维护的要求,结构健康监测技术近年来得到了广泛的研究与应用。基于Lamb波的损伤识别方法对小损伤敏感,灵敏度和精度较高,其中主动Lamb波技术可以对结构中的裂纹、表面腐蚀和焊接缺陷等多种损伤模式进行在线识别,是目前采用较多的一种识别方法[1]。在已有的主动Lamb波损伤识别方法中,比较常用的一般是以结构健康状态下的响应为参考信号,通过对比损伤状态下的响应从而可以得到由损伤产生的散射信号,利用几何方法实现损伤定位。以损伤散射信号的飞行时间为损伤特征信息,通过椭圆定位技术实现损伤定位是一种较为直接的方法[2-4]。如图1(a)所示,利用3个由Lamb波波速及损伤散射信号飞行时间所确定的椭圆轨迹的交点可以实现损伤定位。这一技术实现的前提在于准确获取结构中Lamb波的传播速度及各传感器接收信号的到达时刻。然而,当结构在实际服役的过程中,由于温度、振动和噪声等环境因素的影响,给Lamb波信号的测量带来了很大的不确定性。如图1(b)所示,3个椭圆轨迹不再相交于一点,因此传统的确定性方法已无法满足实际的情况。有学者在传统椭圆定位的基础上提出了概率成像的方法,采用高斯分布函数来确定结构上任意位置出现损伤的概率密度函数,从而对复合材料分层[5]、水下结构腐蚀[6]以及钢管焊接缺陷[7]等多种模式进行了研究。Niri等[8]考虑了Lamb波波速与飞行时间的不确定性,利用扩展卡尔曼滤波技术实现了损伤位置的定位。Yan[9]利用贝叶斯识别理论在考虑建模与测量不确定的条件下实现了损伤定位。以上的概率法一般是基于给定分布形式的假设前提下进行的,当外界因素影响较小时,假设近似成立,识别的结果也较为准确。但是,实际情况中,来自外界的影响因素多种多样,影响程度也难以准确量化,这使得先前假设的分布形式难以满足实际条件,会影响结果的可靠性。因此,有必要引入非参数估计法来消除对假设的依赖。核密度估计作为一种常用的非参数估计方法,可以在不需要任何分布形式假设的条件下得到关于现有样本的准确估计,在工程领域内得到了广泛应用[10-11]。近年来,研究较多的算法还有时间反转法[12-13]、偏移法[14]、相控法[15]和空间滤波器[16]等。
在研究基于Lamb波损伤识别的同时,数值模拟技术对研究Lamb波在结构中的传播规律具有重要意义。目前的方法主要有有限元法、有限差分法和边界元法等。由于Lamb波最小波长的数量级有时达到毫米级,采用传统的方法需要耗费大量的计算资源。谱元法具有谱单元的高效性,同时也兼备了有限元的灵活性,是模拟Lamb波传播过程的一种非常有效的方法[17-19]。Ha等[20-21]利用谱元法模型分析了压电片与结构之间粘接层的厚度对信号的影响。Zak等[22]基于谱元法对铝板和复合材料结构进行了损伤识别。
笔者借助谱元法的数值模拟技术,利用核密度估计法实现损伤定位。首先,建立了压电-结构耦合的三维谱元法模型,分析了铝板结构中Lamb波的传播特性,利用Morlet小波变换得到信号的到达时刻,从而得到Lamb波在结构中的传播速度;其次,通过对Rayleigh-Lamb方程的数值分析,求解铝板中Lamb波的频散曲线,得到Lamb波的理论传播速度;最后,利用核密度估计方法,在3种水平的高斯白噪声下,对含有小孔损伤的铝板进行了概率损伤识别,得到了损伤位置的概率密度函数。
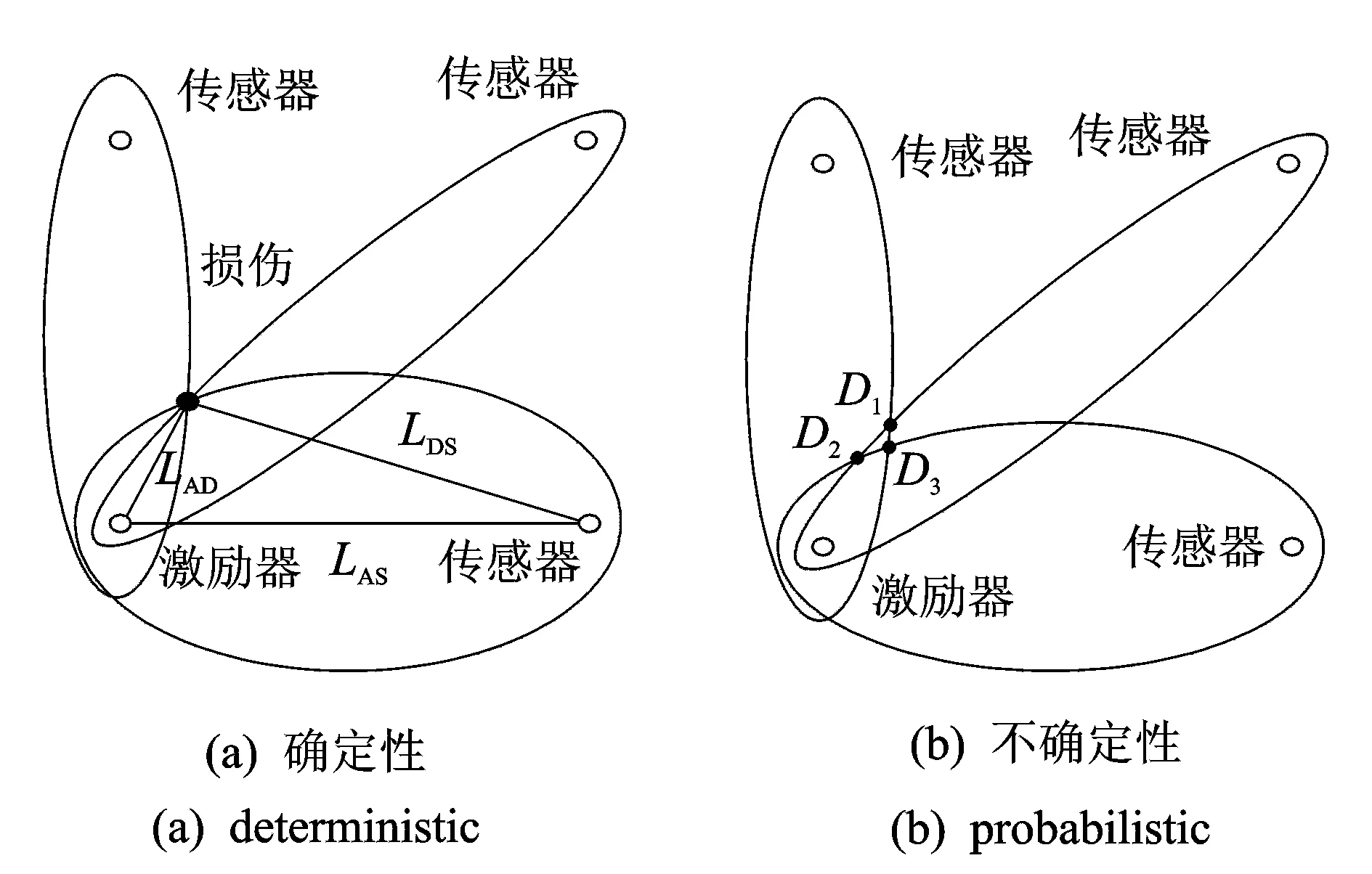
图1 基于飞行时间的椭圆损伤定位
2 数值仿真模型
2.1 三维谱元法的建立
在谱元法中,通过N阶Legendre多项式得到单元的N+1个Gauss-Lobatto-Legendre(GLL)节点坐标,表示为
(1)
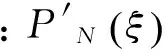
单元节点的局部坐标如下:ξ1=-1;ξ2=-0.765 055;ξ3=-0.285 232;ξ4=0.285 232;ξ5=0.765 055;ξ6=1。
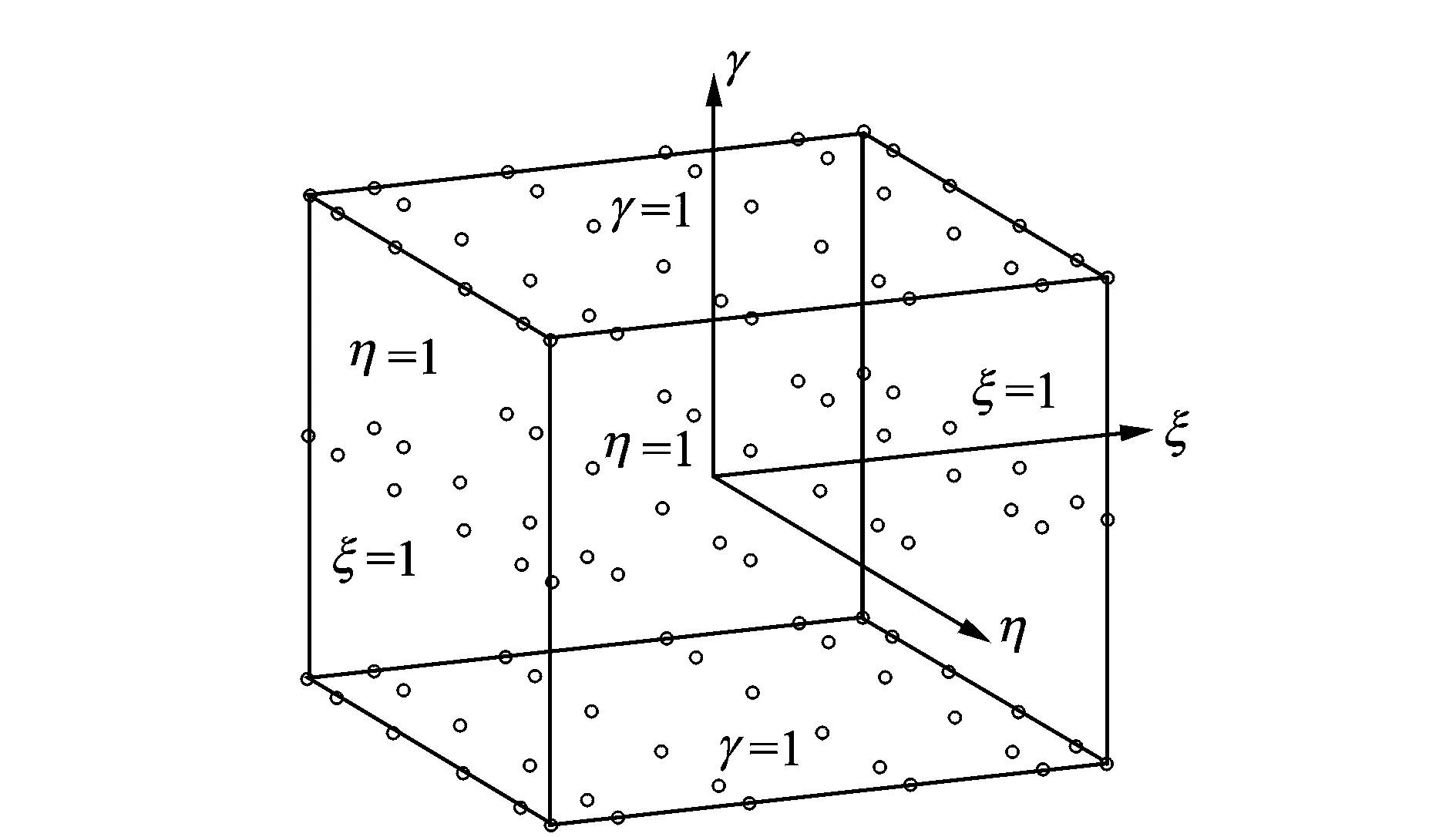
图2 参考系中108节点的三维谱单元
图2为笔者所采用的6×6×3节点的三维谱单元在局部坐标系中的示意图。
根据Lagrange插值多项式构造形函数,则单元内的位移函数可表示为
(2)
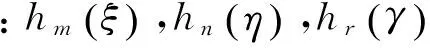
(3)
其中:δmn为Kronecker符号;ωm为GLL权系数。
这样就可以形成单元刚度矩阵、质量矩阵及载荷向量。
2.2 压电-结构耦合分析
在损伤识别过程中,Lamb波的激发与接收一般由压电片完成,因此有必要建立压电片与结构耦合的数值模型来研究Lamb波在结构中的传播过程。压电材料的本构方程[23]可表示为
(4)
其中:σ为应力矢量;ε为应变矢量;E为电场强度矢量;D为电位移矢量;C为弹性常数矩阵;e为压电耦合系数;g为介电常数矩阵。
通过哈密顿变分原理可得到压电材料最终的运动方程[23]为
(5)
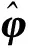
消去式(5)中的电势矢量可得
(6)
其中:KI为机电耦合作用引起的与电压边界条件有关的耦合刚度矩阵;fa为压电片形成的等效作用力。
当压电片作为激励器产生Lamb波时,压电片上表面电压为V,下表面电压为零,则在结构上产生的等效作用力为
(7)
当压电片作为传感器接收Lamb波时,压电片上产生的电势分布为
(8)
3 Lamb波在铝板结构中的传播
3.1 数值模拟
利用已建立的压电-结构耦合的三维谱元法模型,对铝板结构中的Lamb波传播过程进行数值模拟,本节分析的铝板为完好无损伤结构。
图3 激励器、传感器及损伤在铝板上的示意图(单位:m)
如图3所示,铝板尺寸为500 mm×500 mm× 2mm,边界条件为4边自由,铝板的力学参数如表1所示。板上共有4块压电片,其中1块为激励器激发Lamb波,其他3块为传感器,压电片的直径为10 mm,厚度为1 mm,材料参数如表2所示。采用的激励信号为中心频率200 kHz的正弦调制信号,幅值为30 V。

表1 铝板的力学参数
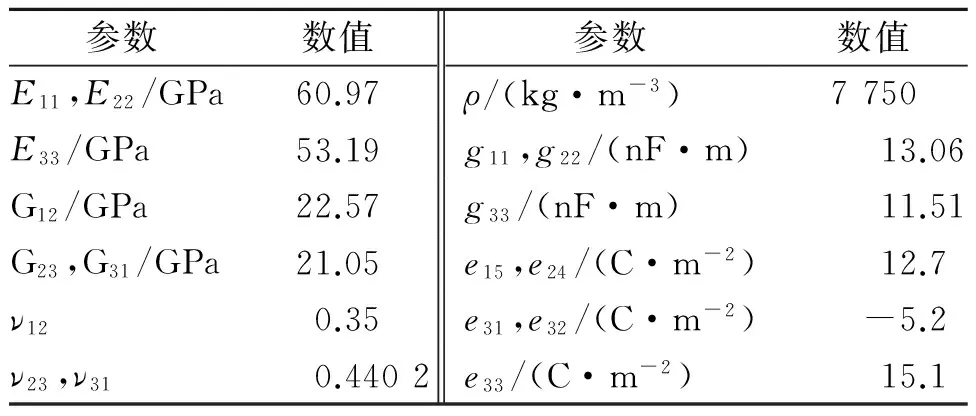
表2 压电片的材料参数
图4所示为5周期正弦调制的激励信号与传感器1及传感器2接收到的Lamb波信号,传感器3接收到的信号与传感器2一致。
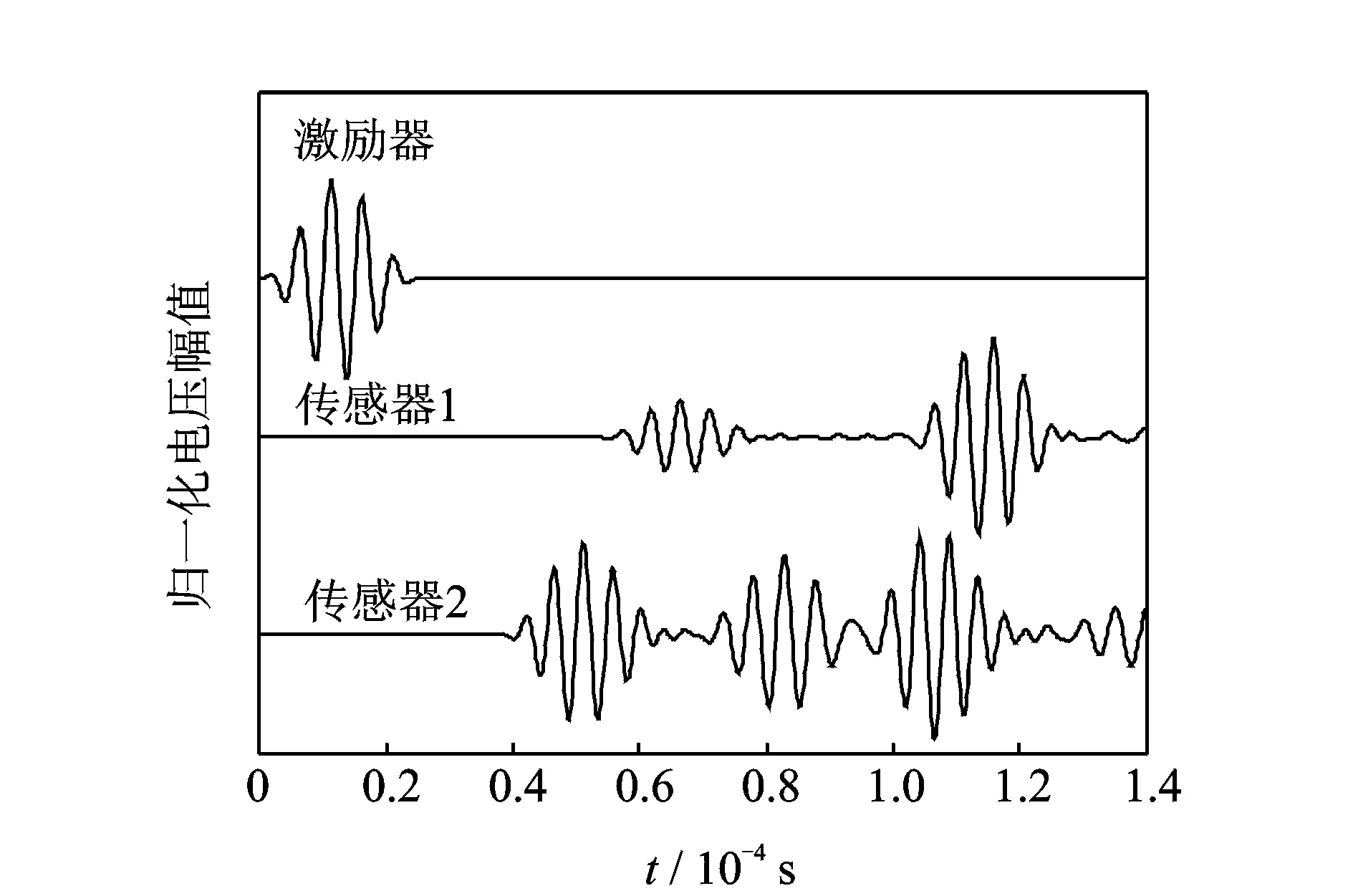
图4 激励信号与传感器1,2的接收信号
3.2 连续小波变换分析
为了准确测得Lamb波到达各传感器的时刻,本节采用小波变换技术计算Lamb波的群速度。其中,Lamb波模式可分为对称模式Si和反对称模式Ai,相应下标分别表示第i阶对称模式和反对称模式。连续小波变换的高时频分辨率可以有效地提取信号中的特定成分。
信号s(t)的连续小波变换(continuous wavelet transform,简称CWT)可表示为
(9)
其中:上标*表示复共轭;a,b分别表示尺度、时间因子。
本节采用的Morlet复数小波定义如下
(10)
其中:fb,fc分别为频率带宽及中心频率。
图5表示的是图4中的信号所对应的小波变换结果,从图5中可以直接得到Lamb波的飞行时间,从而可以计算出Lamb波的群速度。
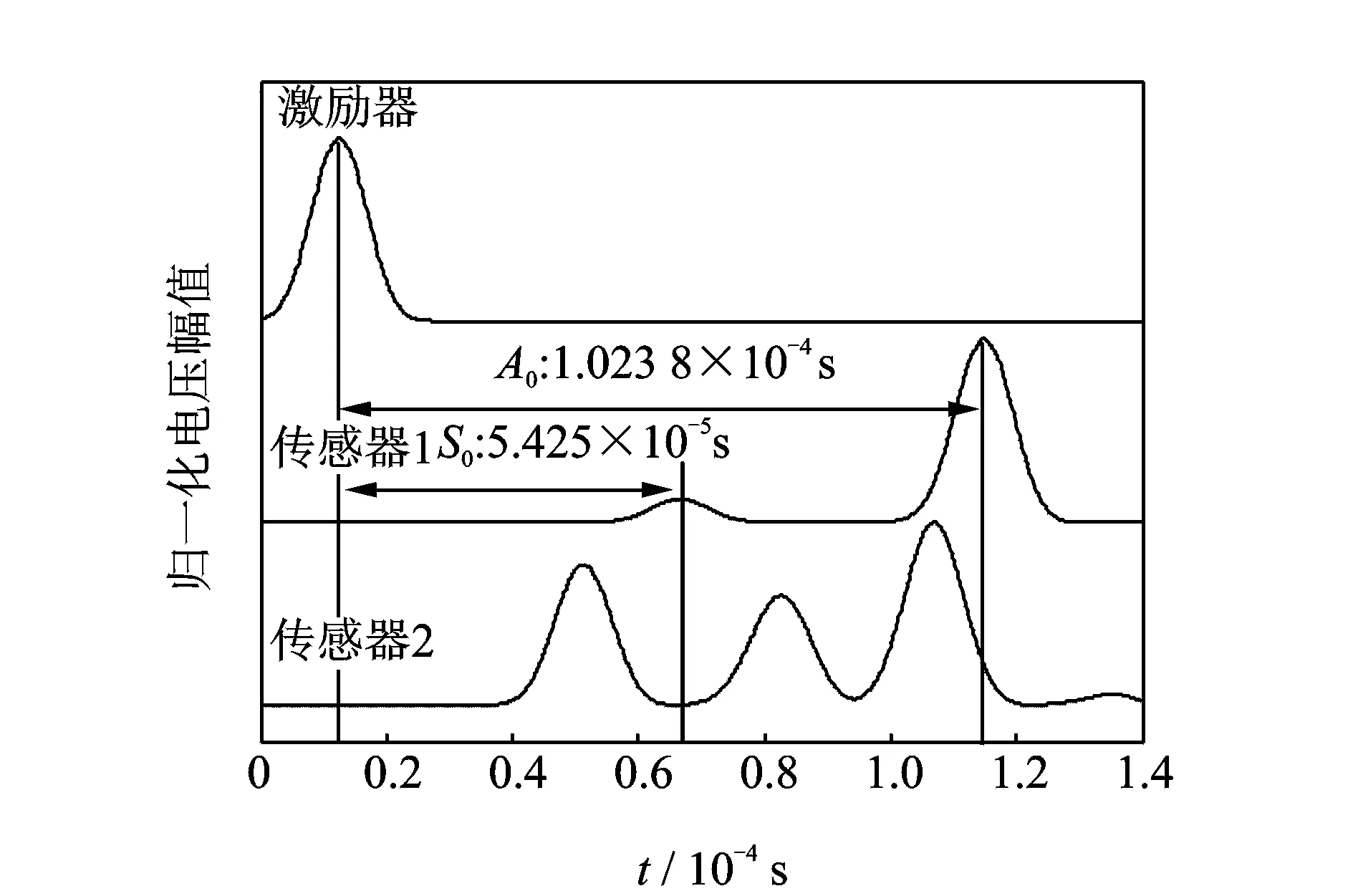
图5 激励信号与接收信号在200 kHz下的小波变换
3.3 Rayleigh-Lamb频率方程分析
平板中Lamb波可用Rayleigh-Lamb频率方程表达如下。
对称模式
(11)
反对称模式
(12)
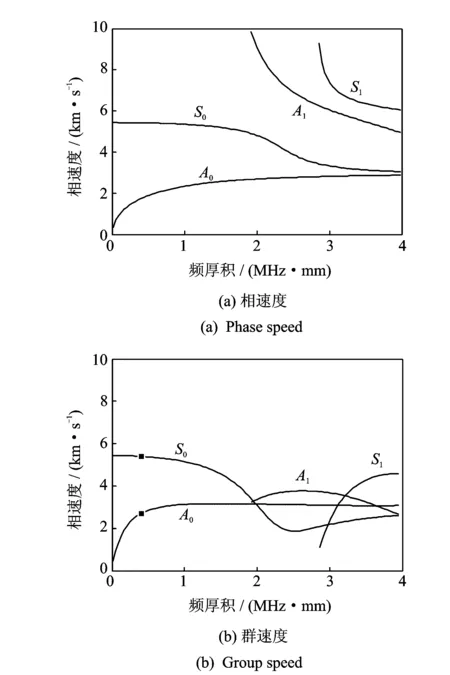
图6 铝板中Lamb波的频散曲线
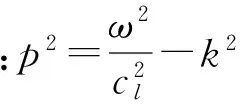
对式(11)、式(12)的频散方程进行数值分析,可以得到Lamb波的相速度与群速度的频散曲线,如图6所示,从图中可以得到频厚积为200×0.002=0.4 MHz·mm时Lamb波的理论速度。同时,在Abaqus中建立相同的压电-结构耦合的三维有限元模型。将3种方法得到的结果进行对比,结果如表3所示。由表3可以发现,A0与S0的速度误差均在5%以内,从而证实了所建立的谱元法模型的准确性,而误差可能由数值积分、网格等因素引起。
表3 不同方法得到Lamb波A0与S0速度对比
Tab.3 Comparison ofA0andS0speeds calculated by different methods
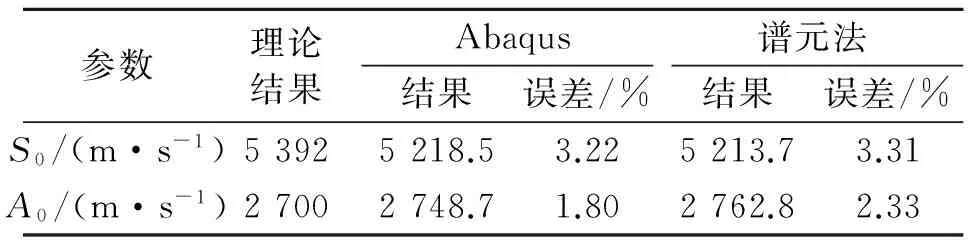
参数理论结果Abaqus谱元法结果误差/%结果误差/%S0/(m·s-1)53925218.53.225213.73.31A0/(m·s-1)27002748.71.802762.82.33
4 Lamb波在铝板结构中的传播概率损伤识别4.1 核密度估计方法
设有一组数据xi(i=1,2,…,n),则可以得到任意一点x处的核密度估计为
(13)
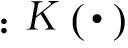
带宽h越大,估计的密度函数就越平滑,误差也会越大;如果带宽较小,估计的密度函数和样本拟合较好,但是不够光滑。带宽优化的一般原则是使得渐进均方积分误差(AMISE)最小。
笔者选用的核函数为高斯核函数
(14)
相应的最优带宽为
h=1.06σn-1/5
(15)
其中:σ为数据的标准差。
4.2 损伤识别结果
通过数值模拟可以分别得到Lamb波在铝板完好结构与小孔损伤下的传播特性。通过小波变换得到3个传感器接收到的损伤散射信号的飞行时间。
为了考虑环境因素的影响,这里讨论3种水平下的高斯白噪声。其中,健康信号的信噪比分别为15,25,35 dB;损伤信号的信噪比相应地为10,15,20 dB。以25 dB/15 dB为例,图7给出了3组损伤散射信号的飞行时间的概率密度分布,由30个测试数据计算所得。
将损伤散射信号的飞行时间Ti代入式(16)的椭圆方程,可得到1组3个椭圆轨迹,两两组合求得3个满足条件的交点,取三交点的平均值作为损伤位置的概率点。
(16)
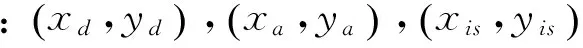
同时,对信噪比35 dB/20 dB的情况进行了分析,计算了30个测试数据,图10给出了识别结果。对比图9和图10可以发现,当提高信噪比时,可能出现损伤的位置将更趋于集中,这将有利于决策者对损伤的判断。
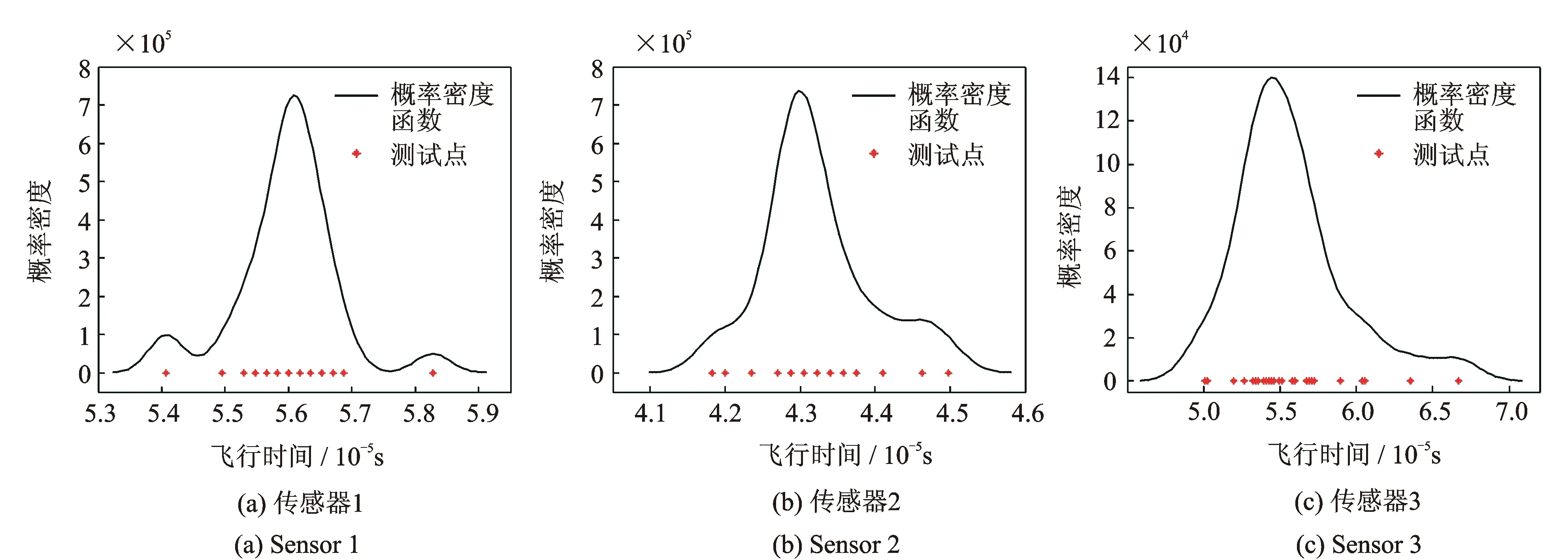
图7 损伤散射信号飞行时间的概率密度函数
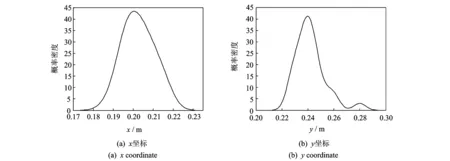
图8 识别的损伤位置的概率密度分布
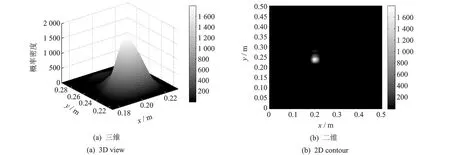
图9 25dB/15dB噪声水平下识别的损伤位置的联合概率密度函数
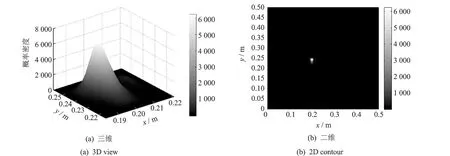
图10 35dB/20dB噪声水平下识别的损伤位置的联合概率密度函数
为进一步论证该方法的有效性,将噪声水平继续降低,即健康信号与损伤信号的信噪比分别取15 dB与10 dB。图11(a)为该噪声水平下通过传感器3得到的一组损伤散射信号的飞行时间的概率密度函数,由40个测试数据计算所得。从图中可以发现,其中部分数据已完全失效,甚至出现了小于零的情况,此时的噪声已经严重影响了部分信号的准确测量。因此,有必要对数据进行修正,即剔除失效数据,最终保留了29个有效数据,重新计算得到新的概率密度函数,如图11(b)所示。同时,分别给出该噪声水平下损伤位置的识别结果,如图12所示。可以发现,随着信噪比的降低,可能出现损伤的区域将进一步扩大。表4给出了3种噪声水平下识别出的损伤概率峰值位置与真实位置的对比,其中误差表示识别位置到真实位置的距离与传感器间的最短距离d的比值,d=0.2 m。
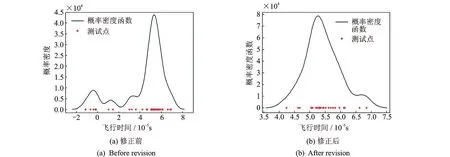
图11 传感器3得到的损伤散射信号的概率密度函数
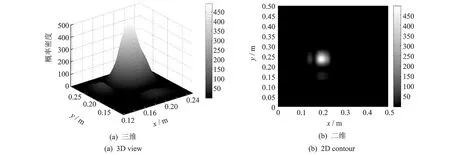
图12 15 dB/10 dB噪声水平下识别的损伤位置的联合概率密度函数
表4 3种噪声水平下损伤位置识别结果与真实值的对比
Tab.4 Comparison of identified damage locations with actual central location under three levels of noise

真实损伤位置/m噪声水平15dB/10dB噪声水平25dB/15dB噪声水平35dB/20dB识别结果/m误差/%识别结果/m误差/%识别结果/m误差/%(0.195,0.245)(0.1979,0.2344)5.49(0.2007,0.2396)3.93(0.1987,0.2440)1.92
5 结 论
1) 基于谱元法建立了压电-结构耦合的三维谱元法模型,分析了Lamb波在铝板中的传播特性。
2) 利用Morlet小波变换准确提取了Lamb波在铝板中的飞行时间,从而得到Lamb波的群速度。通过数值分析,对Rayleigh-Lamb方程进行求解,得到Lamb波的理论速度,并将其与谱元法和Abaqus得到的结果进行了对比,最大误差均小于5%,从而证实了所建立的三维谱元法模型的准确性。
3) 引入核密度估计方法进行概率损伤识别,分别讨论了3种噪声水平下损伤识别效果。结果表明,即使在低信噪比的情况下,识别出的损伤位置的最大误差也仅为5%左右,证实了核密度估计方法能够有效地给出损伤位置概率密度函数,从而能够帮助决策者对损伤的判断。
[1] Su Zhongqing, Ye Lin, Lu Ye. Guided Lamb waves for identification of damage in composite structures: a review[J]. Journal of Sound and Vibration, 2006, 295(3): 753-780.
[2] Lemistre M, Balageas D. Structural health monitoring system based on diffracted Lamb wave analysis by multiresolution processing [J]. Smart Materials and Structures, 2001, 10(3): 504.
[3] Su Zhongqing, Ye Lin, Bu Xiongzhu. A damage identification technique for CF/EP composite laminates using distributed piezoelectric transducers [J]. Composite Structures, 2002, 57(1): 465-471.
[4] Tua P S, Quek S T, Wang Q. Detection of cracks in plates using piezo-actuated Lamb waves [J]. Smart Materials and Structures, 2004, 13(4): 643.
[5] Su Zhongqing, Cheng Li, Wang Xiaoming, et al. Predicting delamination of composite laminates using an imaging approach [J]. Smart Materials and Structures, 2009, 18(7): 074002.
[6] Lu Xi, Lu Mingyu, Zhou Limin, et al. Evaluation of welding damage in welded tubular steel structures using guided waves and a probability-based imaging approach[J]. Smart Materials and Structures, 2011, 20(1): 015018.
[7] Chen Jiangang, Su Zhongqing,Cheng Li. Identification of corrosion damage in submerged structures using fundamental anti-symmetric Lamb waves [J]. Smart Materials and Structures, 2010, 19(1): 015004.
[8] Niri E D, Salamone S. A probabilistic framework for acoustic emission source localization in plate-like structures [J]. Smart Materials and Structures, 2012, 21(3): 035009.
[9] Yan Gang. A Bayesian approach for damage localization in plate-like structures using Lamb waves [J]. Smart Materials and Structures, 2013, 22(3): 035012.
[10]Yu Long, Su Zhongqing. Application of kernel density estimation in Lamb wave-based damage detection [J]. Mathematical Problems in Engineering, 2012, 2012: 406521.
[11]Zhang Baoqiang, Chen Guoping, Guo Qintao. Static frame model validation with small samples solution using improved kernel density estimation and confidence level method [J]. Chinese Journal of Aeronautics, 2012, 25(6): 879-886.
[12]邱雷, 袁慎芳, 张逍越, 等. 基于 Shannon 复数小波的复合材料结构时间反转聚焦多损伤成像方法[J]. 复合材料学报, 2010, 27(2): 101-107.
Qiu Lei, Yuan Shenfang, Zhang Xiaoyue, et al. Shannon complex wavelet and time reversal focusing based multi-damage imaging method on composite structures [J]. Acta Materiae Compositae Sinica, 2010, 27(2): 101-107. (in Chinese)
[13]Watkins R, Jha R. A modified time reversal method for Lamb wave based diagnostics of composite structures [J]. Mechanical Systems and Signal Processing, 2012, 31: 345-354.
[14]Lin X, Yuan F. Experimental study applying a migration technique in structural health monitoring [J]. Structural Health Monitoring, 2005, 4(4): 341-353.
[15]胥保春, 袁慎芳, 邱雷. Lamb 波与瞬时相位技术在损伤识别中的应用[J]. 振动、测试与诊断, 2010, 30(3): 240-244.
Xu Baochun, Yuan Shenfang, Qiu Lei. Damage detection based on technology of Lamb wave and instantaneous phase[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(3): 240-244. (in Chinese)
[16]王瑜, 袁慎芳, 邱雷, 等. 主动 Lamb 波中的空间滤波器结构健康监测[J]. 振动、测试与诊断, 2011, 31(6): 794-797.
Wang Yu, Yuan Shenfang, Qiu Lei, et al. Direction filter method in active structural health monitoring[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(6): 794-797. (in Chinese)
[17]Kim Y, Ha S, Chang F K. Time-domain spectral element method for built-in piezoelectric-actuator-induced lamb wave propagation analysis[J]. AIAA Journal, 2008, 46(3): 591-600.
[18]Kudela P, Ostachowicz W,ak A. Damage detection in composite plates with embedded PZT transducers[J]. Mechanical Systems and Signal Processing, 2008, 22(6): 1327-1335.
[19]Peng Haikuo, Meng Guang, Li Fucai. Modeling of wave propagation in plate structures using three-dimensional spectral element method for damage detection[J]. Journal of Sound and Vibration, 2009, 320(4): 942-954.
[20]Ha S, Chang F K. Optimizing a spectral element for modeling PZT-induced Lamb wave propagation in thin plates [J]. Smart Materials and Structures, 2010, 19(1): 015015.
[21]Ha S, Chang F K. Adhesive interface layer effects in PZT-induced Lamb wave propagation [J]. Smart Materials and Structures, 2010, 19(2): 025006.
[23]Wang S Y. A finite element model for the static and dynamic analysis of a piezoelectric bimorph [J]. International Journal of Solids and Structures, 2004, 41(15):4075-4096.

10.16450/j.cnki.issn.1004-6801.2015.06.009
*航空科学基金资助项目(2012ZA52001);江苏高校优势学科建设工程资助项目
2013-11-15;
2013-12-21
TB559; O212.7
孙汝杰,男,1990年5月生,博士研究生。主要研究方向为结构损伤识别和结构优化设计。曾发表《The impact force identification of composite stiffened panels under material uncertainty》(《Finite Elements in Analysis and Design》2014,Vol.81)等论文。
E-mail:sunrujie@nuaa.edu.cn

