变换方式 品味语言

莫丽娟

【关键词】应用题 解题策略

初中数学

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2015）05A-

0074-02

初中数学应用题中常见的类型有：（1）行程与工程问题，初中阶段主要是考查该部分的列方程解应用题，分为行程问题中的追及与相遇，工程问题中的工程定位、大小等;（2）生产问题，工农业生产中产值、计算率、调配等问题;（3）决策与营销问题，销售活动的盈利、定价、利润率等问题，需要结合数据处理方法和有关信息，进行分析、计算与决策;（4）物理化学问题，与实验数据紧密联系;（5）图像与信息处理问题，数形结合，借助图像处理数据;（6）增长率问题;（7）几何问题。初中数学应用题形式灵活，解题方法多样，关键是需要通过发现知识与问题形成的规律，寻找解决问题的思路，循序渐进地构建知识网络，掌握扎实的技术与方法，与实际生活问题相结合，仔细分析问题的提问方式，摸索细节，构建数学模型，进一步解决问题。

一、创设有效情境，深入学习理论

初中数学应用题是将相关理论知识与实际数字结合起来，考核与生活、生产实际相关的一些问题。基于应用题的考核方法与新课改理念下的教学目标，教师要创设有效的教学情境，引导学生在具体的情境中分析问题，厘清问题思路，分析出问题的已知条件、限制因素和求解问题，通过情境的激励和辅助作用，有效促进学生找出解决问题的方法与策略。创设情境有如下方式：一是运用直观的教学手段创设情境，如线段图、实物等，借助这些东西创设直观的教学场景，通过将抽象的问题具体化，简化解题思路;二是多媒体情境，运用信息技术手段，将抽象化为具体，将静态转化为动态，化繁为简、化难为易，提升学生的学习积极性和主动性，调动学生思维的灵活性;三是通过设疑创设情境，让学生在问题的关键处设疑，引导学生摸索出线索，完善学生的认知结构，强化学生的综合能力。

例如：“快车与慢车在平行轨道上相向而行，快车长100m，慢车长150m，快车驶过慢车某个窗口用时5s。问慢车驶过快车某个窗口所用时间？”对于此类问题，可以借助多媒体模拟实际运行过程，使得数学问题形象化，加深学生的印象，达到有效解题的目的。应用题的解答需要学生综合分析社会生活实际，结合数学科学基础理论，创设有效情境，将数学元素融入到现实元素中，综合分析应用题的因果关系、限定条件等，找出思路，按图索骥。

二、实施生活指导，解决实际问题

初中数学问题与生活、生产实际联系紧密，为强化学生的应用能力，实现新课改教学目标，在初中数学应用题教学中，教师应重视实施生活指导，引导学生分析应用题中对周围环境的数量关系以及实际问题的反映，结合数学知识，探究实际问题的解决过程，由此强化学生的科学素养与应用能力。将生活中常见的问题引入到数学应用题中，也可以有效激发学生的学习兴趣，鼓励学生互助合作、实际探究，强化学生的综合能力。

例如，某地实行医保制度，每位居民年初缴纳医保70元，医疗费用结算方式分3部分，不超过n元的部分全部由医保基金承担;超过n元不超过6000元的部分由个人承担k%，其余由医保基金承担;超过6000元部分，个人承担20%，其余由医保基金承担。设某居民一年看病医疗费用为x元，个人实际承担医疗费用（年初社保缴纳基金与医疗费用中个人承担费用之和）为y元。（1）y与x的函数关系（含n、k、x的代数式）;（2）给出3对数据，个人看病所花费医疗费x（元）与个人实际承担医疗费用y（元）分别为（400，70）、（800，190）、（1500，470），求n、k的值？对于该类问题，教师应该运用生活指导法，将此问题与实际生活紧密联系，引导学生分析生活中出租车、水电费计费方式，结合分段函数、定义域、数形结合相关知识展开分析。根据实际问题需要，划分x为（0，n）、（n，6000）、（6000，+∞）三个区间段，再通过数形结合画出折线图，运用问题2中的3组对应数据列出方程组，就可以得出正确的解答。通过实际生活问题指导，能有效解决初中数学应用题中的营销与决策问题、行程问题等，以此强化学生的应用能力与数学素养。

三、应用阅读指导，按图索骥解题

阅读指导是解决应用题的关键，如果忽略了某部分的要点，可能找不到解决问题的切入口，或者解出来的答案又不符合实际问题的需要，导致增解、误解等。应用阅读指导学习方案，引导学生按图索骥、循序渐进地找到出口、厘清思路、制订方案、完善过程。数学语言具有简洁、无歧义等特点，但同时其又具有内涵丰富、抽象性，尤其是需要将数学符号语言、图表语言等在阅读过程中进行转换。所以，指导学生科学阅读，能取得事半功倍的效果。需要注意如下几点：一是略读识大意，快速浏览，分清是哪类问题（不等式、数列、函数、概率），厘清已知条件和求解问题，以及涉及的数学知识，画出示意图;二是细读抓关键，将关键句子与语句找准，辨析其延伸出的综合知识与数学问题，逐句研读，找准关键;三是精读勤转换，将抽象问题具体化，数学问题形象化，运用符号、图表等表述形式，灵活转换思维，厘清解题思路。

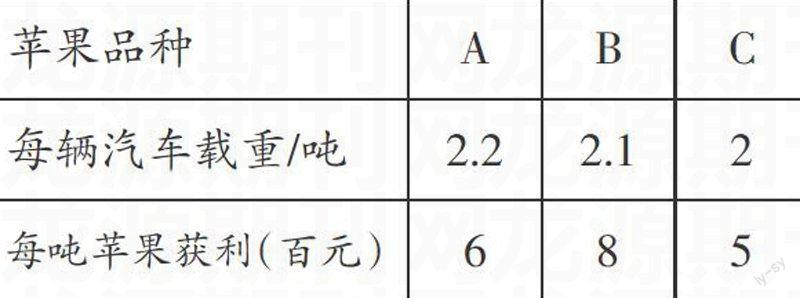
例如，装运方案设计中，某乡组织20辆汽车装运A、B、C类苹果共42吨到外地销售，每辆车装同一种苹果且装满，每种苹果不少于2车。（如下表）

对于A、B、C三类苹果品种，其每辆汽车运载量（吨）与每吨苹果获利（百元）对应的数据分别为（2？郾2，6）、（2？郾1，8）、（2，5）。问（1）若分别用x、y辆车装运A种苹果，问x与y的函数关系式，并求出x的取值范围？（2）若要利润最大，如何分配车辆？对于该类型的题目，可以建立函数模型，结合实际问题以及题目要求，仔细阅读，找到“每种苹果不少于2车”“最大利润”等关键语句，建立函数关系式，得出答案，即x=2。

四、展开数学建模，强化科学思维

数学建模是解决初中数学应用题的关键思想，在阅读材料、厘清题意的基础上，将应用题中实际阐述的问题抽象成数学语言，通过深入加工、去粗存精、抽象概括、数形结合，有效运用数形结合建立出相应的数学模型。从实际问题到纯数学问题，经过了数学语言的转换和信息加工，以及对原有知识、信息和生活经验的提取和加工，是复制信息处理的过程。数学建模需要注意：一是扎实掌握数学理论知识、数学思想、数学方法;二是归类分析、准确建模，将应用题中阐述的问题进行分类，如生产问题、形成问题、决策问题、几何问题、浓度问题等，通过信息筛选、转换，将应用题中的实际问题转换为数学符号、图形语言、数量关系等，构建数学模型。

例如，一条直线上依次有A、B、C、D、E五个点，问图中共有几条线段？又如往返于甲乙两地的客车，中途有3个站，问需要准备多少种车票？这类型的问题可以建立几何图形模型，结合线段图展开分析。再如计算机程序为二进制数，转换方式为（1011）2=1×23+0×22+1×21+1×20=11，那么（1001）2换算成十进制数的结果是■？此类型可以建立阅读理解模型。车辆调配、水电费交费、出租车计费等可以建立方程组模型，台风影响相关问题可以建立三角函数模型，几何问题可以建立几何模型，与几何图形相关的知识结合起来，运用数形结合思想解决问题。通过开展数学建模教学，强化学生的数学科学思维，有效引导学生掌握数学思想、数学方法，提升数学科学素养。

按图索骥妙解题，循序渐进促提升。新课改理念下的初中数学教学，需要坚持以学生为本、因材施教的教学策略，认真分析学生的认知基础、实际能力与学习特点，探究学生的知识与能力成长方式，从扎实理论、引导方法、培养思维、强化能力等出发，提升学生的综合素养，实现快速解决初中数学应用题的目标。

（责编 林 剑）