多孔介质方程的格子Boltzmann模型

刘 芳， 赵海龙

（长春工业大学 基础科学学院，吉林 长春 130012）

0 引 言

格子Boltzmann方法（Lattice Boltzmann Method，LBM）是20世纪80年代诞生的一种新兴的计算流体力学方法，它植根于物理学描述气体运动的连续Boltzmann方程以及计算机理论的元胞自动机模型。与传统方法不同，该方法是从微观动力学角度出发，把宏观物理量当作微观量的统计平均结果［1－2］。格子Boltzmann方法诞生以来，已在许多流体问题的数值计算上取得了很大成功。近年来，一些学者将格子Boltzmann方法用于求解其他的线性和非线性偏微分方程，也取得了满意的成果。目前该方法已成为偏微分方程数值解领域除传统方法外的又一个可供选择的新兴数值算法［3－9］。

文中考虑用LBM求解含有非线性源项和非线性扩散项的多孔介质方程［10］：

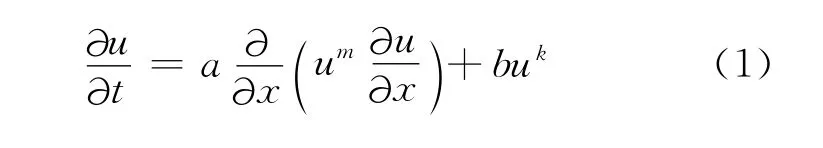
式中，m和k是有理数，a和b是参数，u＝u（x，t），x和t分别表示空间和时间变量，D（u）＝um是非线性扩散项。这类方程经常出现在热和质量传递、燃烧理论和多孔介质流动等非线性问题中。例如，该方程可以描述在静止的介质中，温度是以一个幂率函数变化的热传递过程，一些学者已经用其它方法研究过该方程，例如紧致有限差分方法［11］和Adomian分解法［12］等。但是到目前为止，还没有应用LBM对该方程的相关数值研究，文中将对方程（1）构建一个简单实用的LBM求解模型。

目前LBM已被应用于解决大量的线性和非线性偏微分方程。然而，一般的格子Boltzmann模型在处理非线性扩散项上还有一定的困难。文中通过灵活的选取平衡分布函数，使这一问题得到了很好的解决。

1 多孔介质方程的格子Boltzmann模型

文中考虑的多孔介质方程（1）可以改写为：

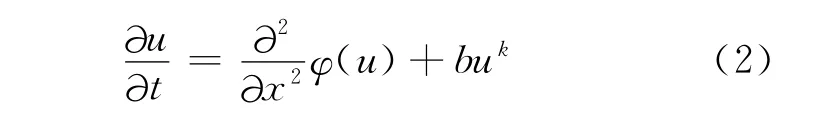
令局部粒子分布函数的演化方程形式如下：

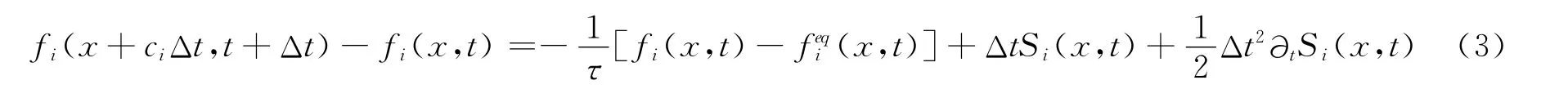
Si（x，t）——源项分布函数；

i——离散速度集合｛c0，c1，c2，…，cN｝的指标。

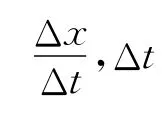
通过实施Taylor展开，Chapman－Enskog展开以及多尺度分析技术，可以从方程（3）恢复出具有二阶精度的方程（2）。这一过程的实施需满足以下几个对平衡态分布函数和源项分布函数的限制条件：

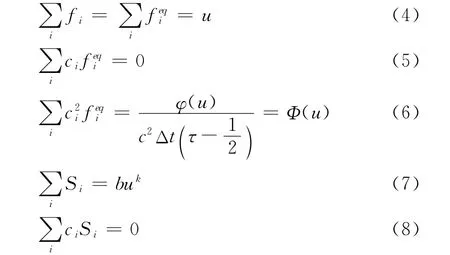
由式（4）～式（6）解得平衡态分布函数分别为：

为了满足式（7）和式（8），取

源项F（x，t）＝buk只针对文中研究的多孔介质方程。方程（1）和方程（2）中的源项可以是u，x和t的其它函数形式。

2 数值模拟

为了检验模型的精度和有效性，我们将对几个多孔介质方程进行数值模拟。定义时间步t＝tj的全局相对误差（GRE）和最大绝对误差（MAE）为：

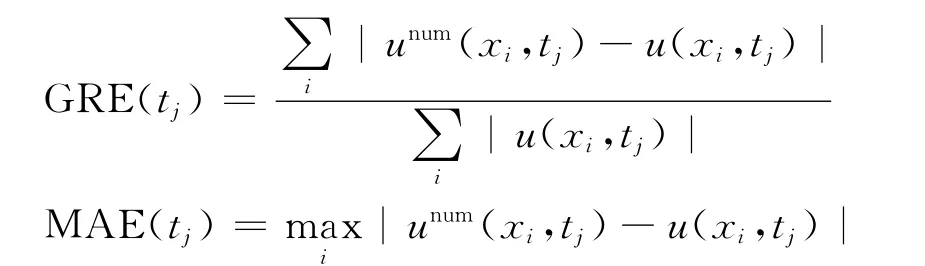
式中：unum（xi，tj），u（xi，tj）——分别为tj时刻点xi处的数值解和精确解；

宏观的初边值条件由精确解确定，对于微观的初始条件，令局部粒子分布函数直接等于局部平衡分布函数，即。演化方程（3）中导数项的计算将采用显示差分格式∂tSi（x，t）＝［Si（x，t）－Si（x，t－Δt）］／Δt计算。边界处理采用Z L Guo［13］的非平衡外推法来确定边界处的粒子分布函数。

在非线性科学中，多孔介质方程是一个非常重要的偏微分方程。下面的例子都是来自于实际物理问题。

例1［10］：取m＝1，k＝0，则方程（1）变成

其精确解为

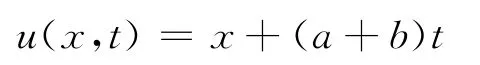
现在取a＝1，b＝1，按照方程（2）改写方程（9）为

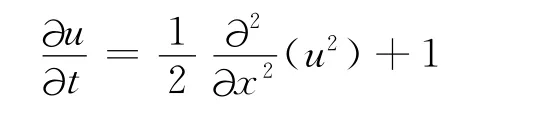
例2［10］：取a＝1，m＝－1和b＝0，则方程（1）变成

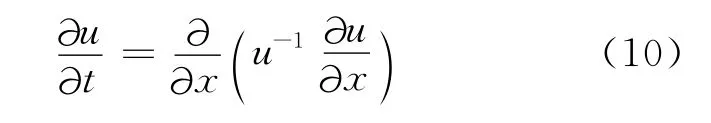
其精确解为

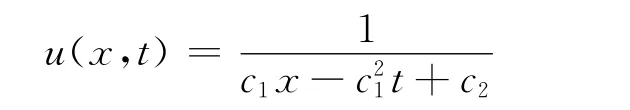
其中c1和c2都为任意常数。简单选取c1＝1，c2＝10，因此精确解变成

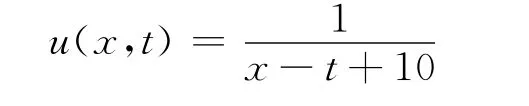
按照方程（2）改写方程（10）为

例3［10］：取和b＝0，则方程（1）变成

其精确解为

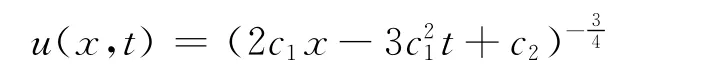
其中，c1和c2为任意常数。简单选取c1＝1，c2＝15，得到

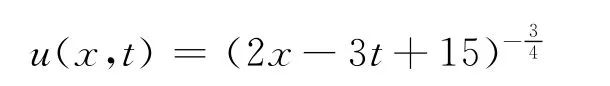
按照方程（2）改写方程（11），有

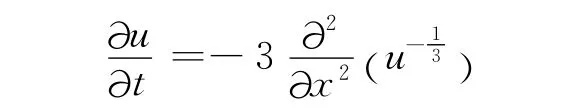
例4［10］：取和则方程（1）变成

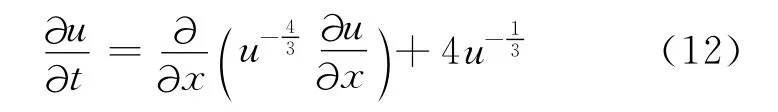
其精确解为

按照方程（2）改写方程（12），有

在数值模拟中，例1～例3选取计算域为［0，1］，例4选取计算域为［2，3］。4个算例的时间步长均为Δt＝0.000 1，空间步长均为Δx＝0.01，自由参数τ的选取依据使t＝1时刻GRE达到最优的原则。例1～例4的τ分别为8.062，9.998，14.002，0.999。在时间t＝1，2，3，4时刻，4个算例的格子Boltzmann数值解与精确解之间的GRE和MAE分别见表1和表2。

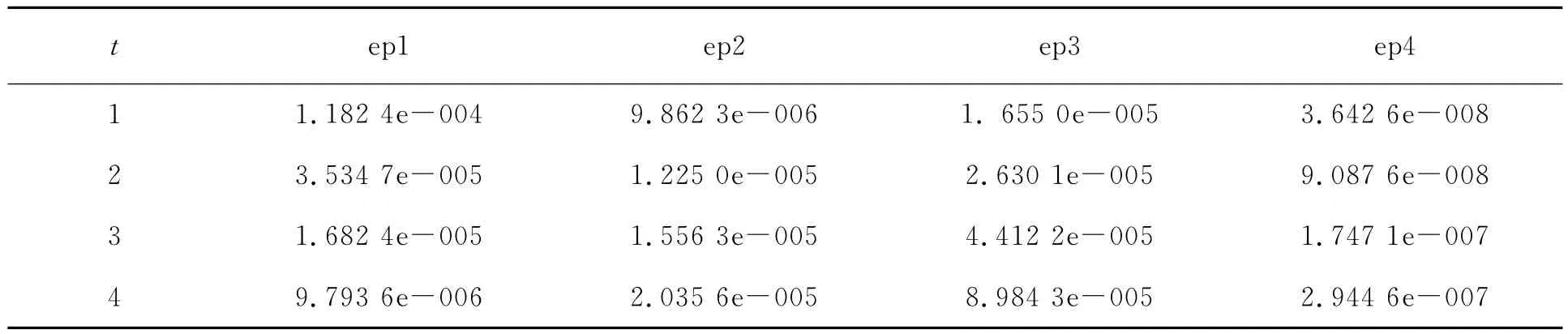
表1 4个算例的不同时间的全局相对误差比较

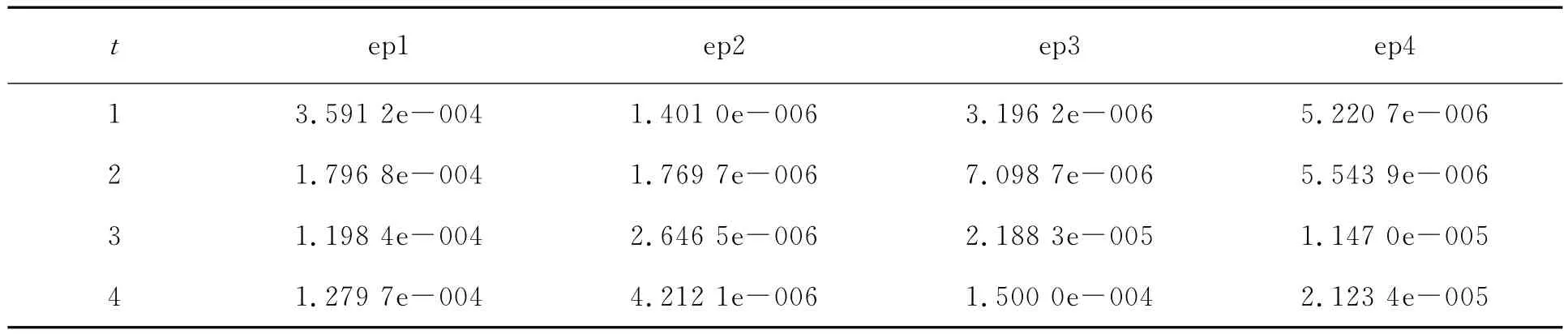
表2 4个算例的不同时间的最大绝对误差比较

表中的数据表明数值解与精确解吻合的非常好，显示了该模型的有效性。

为了检验该方案的实际空间精度，分别在网格数目为16，32，64和128（即Δx＝0.062 5，0.031 25，0.015 625，0.007 812 5）时对4个算例的方程进行数值计算，且保持其它参数不变。t＝1时刻的GRE和MAE与空间步长Δx在对数坐标系下的拟合图如图1所示。

图1 t＝1时刻的空间精度检测

图中所有拟合直线的斜率都在2.0左右，这就验证了该模型在实际计算中达到了空间二阶精度。

3 结 语

对含源项的非线性多孔介质方程构造了一个简单实用的格子Boltzmann模型，通过改造演化方程以及对局部平衡态分布函数的一些限制，恢复出具有二阶精度的宏观方程。除时间步长和空间步长外，计算格式中只有一个自由参数τ。采用D1Q3速度模型，编程简单，计算速度快。对几个典型的多孔介质方程进行了数值模拟，验证了该模型的精度和有效性。该模型同样适用于同类型的其他方程，且可以直接扩展到二维和三维问题。

［1］ R Benzi，S Succi，M Vergassola.The lattice Boltzmann equation：theory and applications［J］.Phys.，1992，222：145－197.

［2］ Y H Qian，S Succi，S A Orszag.Recent advances in lattice Boltzmann computing［J］.Annu.Rev.Comput.Phys.，1995（3）：195－242.

［3］ B C Shi，Z L Guo.Lattice Boltzmann model for nonlinear convection－diffusion equations［J］.Phys.Rev.E.，2009，79：16701.

［4］ I Ginzburg.Truncation errors，exact and heuristic stability analysis of tw－relaxation－times lattice Boltzmann schemes for anisotropic advection－diffusion equation［J］.Commun.Comput.Phys.，2012（11）：1439－1052.

［5］ F Liu，W P Shi.Numerical solutions of two－dimensional Burgers＇equations by lattice Boltzmann method［J］.Commun.Non.Sci.Numer.Simul.，2011，16：150－157.

［6］ H L Lai，C F Ma.A new lattice Boltzmann model for solving the coupled viscous Burgers＇equation［J］.Physica A，2014，395：445－457.

［7］ J Y Zhang，G W Yan.Numerical studies based on higher－order accuracy lattice Boltzmann model for the complex Ginzburg－Landau equation［J］.J.Sci.Comput.，2012，52：656－674.

［8］ B C Shi.Lattice Boltzmann simulation of some nonlinear complex equations［J］.Lect.Notes Comput.Sci.，2007，4487：818－825.

［9］ F F Wu，W P Shi，F Liu.A lattice Boltzmann model for the Fokker－Planck equation［J］.Commun.Non.Sci.Numer.Simul.，2012，17：2776－2790.

［10］ A D Polyanin，V F Zaitsev.Handbook of nonlinear partial differential equations［M］.Boca Raton：Chapman and Hall／CRC Press，2004.

［11］ N Pamuk.Series solution for porous medium equation with a sourceterm by adomian＇s decomposition method［J］.Appl.Math.Comput.，2006，178：480－485.

［12］ M Sari.Solution of the porous media equation by a compact finitedifference method［J］.Math.Prob.Eng.，2009，17：1－13.

［13］ Z L Guo，C G Zheng，B C Shi.Non－equilibrium extrapolation method forvelocity and pressure boundary conditions in the lattice Boltzmannmethod［J］.Chin.Phys.，2002，11：366－374.