提高GPS计亩器坡地测量精度的方法

李会杰， 龚全超， 王天宇， 高 生

（1.长春工业大学 机电工程学院，吉林 长春 130012；2.长春工业大学 电气与电子工程学院，吉林 长春 130012）

1 GPS计亩器测量土地面积的算法

为了准确计算曲面的距离和面积，GPS计亩器是通过卫星定位系统来获取所处位置的经度、纬度和高度，能够达到精确计算地表的距离和面积。选米作为显示单位，计算距离时，通过测量出的两个点的坐标，利用数学公式立即算出两个点之间的距离；计算面积时，若测量的终点和起点没有重合，则GPS计亩器以这两点的直线自动填补数据来计算面积［1］。目前在国内，其他的投影法因计算十分复杂难以在单片机中实现，如高斯一克吕格投影转换。地球是呈椭圆球型的曲面，采用投影的方式，然后转换成平面坐标下进行计算，可以实现精确地计算地表的距离和面积［2－4］。将地球看做是正球体，这样可以简化计算；实际上被测量的农田面积相对较小，需要测量的边界距离也较短，因此，因为简化带来的误差可以忽略不计。取地球半径为6 370km，则可以转换成平面坐标：

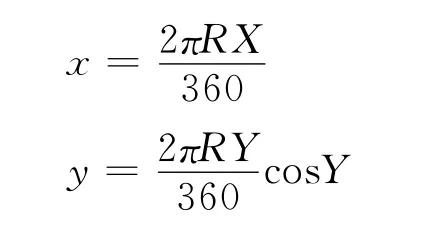
式中：X——经度，m；

Y——纬度，m；

R——地球半径。

那么在地球表面Y经度处，由以上坐标可以计算出纬度差、经度差各为一度的方格面积：

因为经度和纬度的数值比较大，若直接用式（1）来计算面积，计算带来的误差会很大，为了减小计算误差，我们构建一个新的坐标系［5］，以第一点1作为坐标原点，以相对偏移量构成的坐标系，如图1所示。

图1 投影转换后的平面坐标及相对偏移量

有的农田是不规则的多边形，对于这种图形，可以采用计算梯形面积的方法来获得，如图1中的阴影部分，由2，3两个点组成的梯形，其面积为：

则由n点构成的农田面积为：

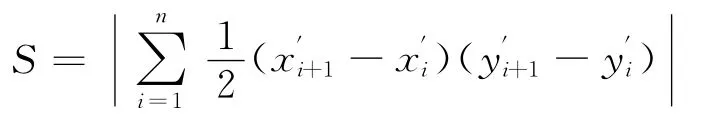
其中

2 GPS测量坡地面积的方法

地形不同、面积不同、形状不同的不同区域进行多次测量，尤其是对坡地一定要采取更多的点进行测量，然后采用投影的方法转换成高斯平面直角坐标，再以平面直角坐标求解面积。

因为地球表面是个不能够展开的曲面，不能简单地将地球曲面拉平，那样会有很多褶皱和裂口，影响计算的精度。这个问题可以采用投影的方法解决地球面不能直接展开的问题，就是通过投影来确定地表曲面与平面上的点位之间的每个对应关系。但是，这样计算的话，又带来一个问题，就是一定会有投影变形产生。下面通过高斯投影构成新的平面直角坐标系——高斯平面直角坐标系，来解决这个问题。假想在地球外表面套上一个平面卷成横圆柱套，以赤道的投影和中央子午线的投影的交点为坐标原点，以赤道的投影作横坐标轴，用y表示，以中央子午线的投影作纵坐标轴，用x表示，构成一个新的称作高斯平面直角坐标系［6］，如图2所示。

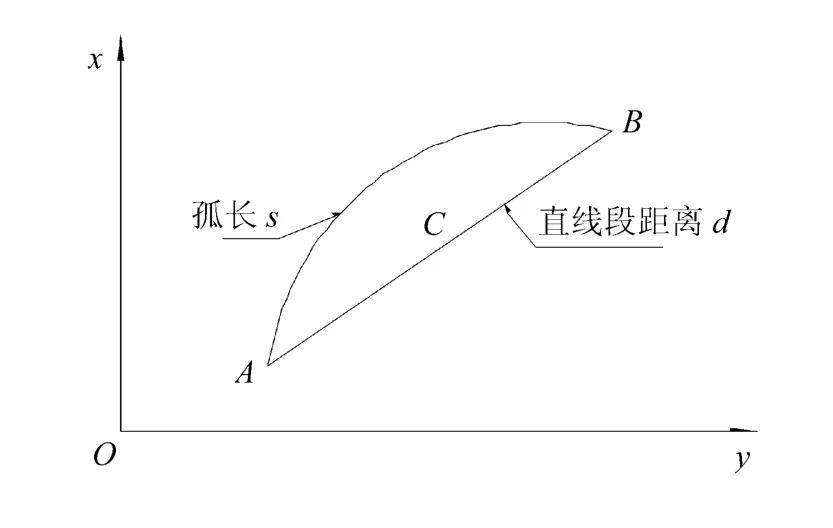
图2 高斯平面直角坐标及投影距离改化

由于高斯投影为正形投影，在中央子午线上的长度没有变形，也没有角度变形。每个投影带都有自己独立的高斯平面直角坐标系。但是，不在中央子午线上的各长度比均大于1，会有变形，如果距离中央子午线很近，则变形较小，反之距离越远，变形也越大。

图2中，设s为大地弧线长，d为两投影点间的直线长度，设地球上两点坐标为：A（x1，y1）、B（x2，y2），A与B的中点坐标为：c（xm，ym），Rm为地球的平均半径，Δy＝y2－y1，则有高斯投影距离改化公式为：

3 GPS测量坡地面积的误差分析

在应用高斯平面直角坐标选择直角坐标系时，选择的直角坐标中，所测量地区的距离距中央子午线距离越近，产生的误差就越小，反之就越大，这就需要刻板地选择中央子午线。这是因为，假设选取10个点的GPS坐标，由于用向量积方法求面积，只需要相对坐标，为了使计算出来的地表面积数值精确，就要越靠近这10个点来选取经线。

以某公园湖心岛为例：选125.318 7°最接近经过湖心岛中心附近。当选取子午线125.318 7°时，计算的面积为16 886.06m2，当选取子午线125°时，计算的面积为16 875.12m2，当选取子午线120°时，计算面积为16 850.60m2。

GPS计亩器计算的结果与选定中央子午线为120°所计算面积相吻合。以子午线125.318 7°为基准，比较一下，GPS计亩器所测得的地表面积和用公式计算面积，相对误差为0.21%，这个误差的原因是高斯投影长度变形的结果。因为高斯投影距离改化只与纬线方向参数y有关，而且在子午线方向上没有长度变形，所以在计算面积时，可把所测地表区域按照子午线的方向分割成小块，这样就可以得出结论——面积变形与距离改化成正比例关系［7］。即：

相对误差为：

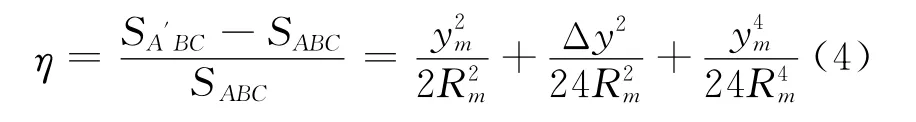
设μ为所测区域东西长度，v为所设经线距离所测区域最远点距离，则μ＝Δy，v＝y2，ym＝把地球平均半径Rm＝6 370km代入式（3）。由此可得出：选定的经线距离所测区域越近，误差就会越小，反之就越大；所测区域越小产生的误差越小，反之越大。

ABC区域的面积修正函数：

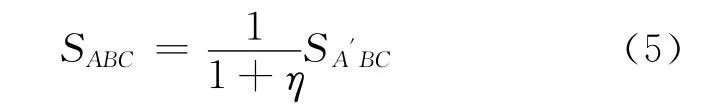
通过实验验证，进行面积修正确实减小了面积的误差，提高了手持GPS计亩器的测量精度。

4 结 语

通过以上分析GPS计亩器面积测量在高斯坐标转换中产生的误差，如果中央经线距离所测地表区域越近产生的误差就越小，越远产生的误差就越大；此外，所测地表区域越小产生的误差也越小，反之也就越大。为此当测量不规则的坡地时，为了减小因为面积变形产生的误差，应该在坐标转换时选择所测区域的平均经度，而不是刻板的选择中央子午线；或对所计算的结果加以修正，修正函数为；要想得到比较精确的坐标，首先，利用测绘部门提供的坐标对GPS计亩器进行校正，其次，选取平均值计算，即利用GPS多次在同一点测量，然后取平均值［8］。如果有所测地表的面积区域较大的情况，那么采用划分区域分别进行计算再求和的方法。

［1］ 刘弘，姚连芳，马杰，等.GM－101型GPS面积测量与精度评价［J］.河南科技学院学报：自然科学版，2008，36（3）：33－35.

［2］ 谷超杰.Excel2003在高斯投影坐标换算中的应用［J］.测绘与空间地理信息，2008，31（6）：190－192.

［3］ 赵廷安，田雪丰.矿区GPS高程拟合精度和可靠性研究［J］.中国煤田地质，2005，17（3）：59－60.

［4］ 刘永义.济宁矿区BJ－54至WGS－84坐标转换模型改进及精度分析［J］.全球定位系统，2010，35（1）：33－37.

［5］ 张秋昭，张书毕，刘军.局部区域GPS网坐标转换的改进模型［J］.全球定位系统，2008，33（5）：62－64.

［6］ 施一民.现代大地控制测量［M］.北京：测绘出版社，2003.

［7］ 路琪，景欣.手持GPS测量面积变形误差研究［J］.全球定位系统，2012，37（3）：63－66.

［8］ 周蓓，陶踅君.手持GPS定位在野外地质测量中的误差分析［J］.资源环境与工程，2009，23（3）：311－313.