基于小波脊线的滚动轴承故障诊断方法
姜万录, 李宁宁, 朱 勇
1. 燕山大学 河北省重型机械流体动力传输与控制重点实验室,河北 秦皇岛 066004;2.燕山大学 先进锻压成形技术与科学教育部重点实验室,河北 秦皇岛 066004)
基于小波脊线的滚动轴承故障诊断方法
姜万录1, 2, 李宁宁1, 2, 朱 勇1, 2
1. 燕山大学 河北省重型机械流体动力传输与控制重点实验室,河北 秦皇岛 066004;2.燕山大学 先进锻压成形技术与科学教育部重点实验室,河北 秦皇岛 066004)
滚动轴承发生故障时的振动信号会呈现丰富的非线性动力学特征。基于小波脊线对非线性、非平稳信号分析优势,提出了基于小波脊线的混沌程度刻画方法用于滚动轴承多类故障诊断。通过对故障振动信号共振频带包络信号提取小波脊线,并与故障振动信号K熵对比。结果表明,小波脊线不仅能识别滚动轴承故障类型,亦能由小波脊线表征的混沌程度反映故障严重与否。
混沌刻画;小波脊线;K熵;故障诊断;滚动轴承
滚动轴承广泛用于工业各种机械装备中,其性能直接影响设备甚至整条生产线的正常运转[1-2]。轴承发生故障时其运行信息会表现出复杂的非线性特点,采用非线性分析方法,能更准确刻画系统的本质特征[3-4]。
轴承故障发生时因其刚度、摩擦力、外载荷等因素变化,振动信号必呈不同程度非线性特性,且在一定程度上表现出混沌特性。因此可应用混沌特征量(如最大Lyapunov指数、关联维数、Kolmogorov熵等)刻画系统的复杂程度,实现故障监测及诊断[5-6]。
小波脊线为基于小波变换更准确的信号处理方法,适用于处理非线性、非平稳信号[7-8]。本文利用小波脊线优势,将其用于混沌运动程度刻画,并引入滚动轴承故障振动信号分析中。通过对从故障振动信号共振频带提取的包络信号进行小波脊线提取,计算轴承故障振动信号K熵(kolmogorov entropy),利用二者相互验证。结果表明,小波脊线不仅可识别滚动轴承故障类型,亦可由小波脊线刻画的混沌程度反映故障严重与否。
为验证方法的有效性,以美国凯斯西储大学轴承数据为例,分别用小波脊线法及K熵进行分析,二者相互验证取得较满意效果,所提基于小波脊线的滚动轴承多故障诊断方法有效性获得验证。
1 小波脊线提取
1.1 小波脊线与瞬时频率关系
小波脊线为在时频平面内由各时刻信号小波系数模取极大值点(即小波脊点)组成的集合,与信号瞬时频率一一对应[9-10],只要正确提取小波脊线即能获得信号的瞬时频率。
任意单分量实信号s(t)可表示为
s(t)=A(t)cos[φ(t)]
(1)
式中:A(t)≥0为瞬时幅值;φ(t)∈[0,2π]为瞬时相位。
信号s(t)的解析信号定义为
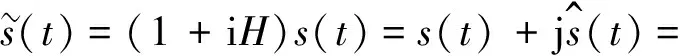
(2)


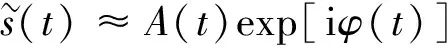
(3)
渐近单分量信号s(t)的瞬时频率可定义为
(4)
选择具有渐近性质的母小波ψ(t),对应的渐近解析小波为
(5)

(6)
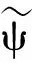
(7)
(8)
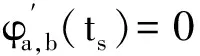
(9)
由上式知,相位驻点是(a,b)的函数。小波脊线(wavelet ridge)定义为在相平面满足ts(a,b)=b所有点(a,b)的集合,小波脊线上点(ar(b),b)称为小波脊点。据上式得
(10)

式(10)说明只要求出信号的小波脊线,即可方便得到信号的瞬时角频率。
1.2 小波脊线与模极大值关系
设实对称窗函数g(t)及Fourier变换分别为
(11)
(12)
将g(t)乘以复正弦波exp(iω0t)可构造出近似渐近解析小波母函数,其时、频域表达式分别为
(13)
(14)
(15)
解析小波函数为
(16)

(17)

(18)
(19)
已知窗函数傅里叶变换G(ω)的模值在ω=0时最大,由式(18)可知,在时刻b处所有小波系数中小波脊点(ar(b),b)处小波系数模值最大。因此,小波脊点与小波系数模极大值点密切相关,只要找到信号小波变换的模极大值点即可确定小波脊线,进而与被分析信号的瞬时频率一一对应关系确定信号的瞬时频率。
1.3 K熵
Kolmogorov熵(简称K熵)类似于热力学中熵的物理意义,用于描述系统运动的混乱或无序程度。考虑一个n维动力系统,将其相空间分割成边长为ε的n维超立方体盒。系统运动时沿相轨道x(t)取极小时间间隔量τ,令P(i0,i1,…,im)表示起始时刻系统在第i0格子中、t=τ时刻在第i1格子中、…、t=mτ时在第im格子中的联合概率,确定系统沿轨道(i0,i1,…,im)运动所需信息量为
(20)
lnP(i0,i1,…,im)
(21)
周期运动的K熵为0;随机运动完全无序,故其K熵趋于∞;在混沌运动系统中,K熵大于零,且K熵越大信息损失速率越大,系统的混沌程度越大,或曰系统越复杂无序。
2 基于小波脊线的轴承故障振动信号分析
为验证本文所提方法的有效性,以美国凯斯西储大学轴承振动数据[13]为例进行分析。滚动轴承型号为6205-2RS JEM SKF,用电火花单点对轴承进行不同程度的损伤,人为制造轴承外、内圈及滚动体故障。损伤点剥落直径分别为0.177 8 mm、0.355 6 mm、0.533 4 mm,深度均为0.279 4 mm,分别记为程度1~3。电机转速1 750 r/min(转频29.17 Hz),采样频率12 kHz。据公式[14]计算获得该轴承外圈故障特征频率为104.56 Hz,内圈为157.94 Hz,滚动体为68.74 Hz。
2.1 外圈故障振动信号分析
由于采集的实际信号中含噪声,计算小波脊线前需对信号进行基于小波包分解的消噪预处理。滚动轴承正常状态下振动信号消噪效果对比见图1。

图1 轴承正常状态下振动信号消噪效果对比Fig.1 Denoising effect comparison of normal bearing vibration signal
对消噪后信号进行相空间重构时用自相关联函数法确定延迟时间。用G-P算法计算关联维数及K熵[15],用饱和关联维数法确定最佳嵌入维数[16]。
计算所得正常状态振动信号的关联积分与超球半径双对数曲线lnC(r)-lnr及嵌入维数分别为1、3、5…29时结果见图2。由图2看出,嵌入维数m=9时曲线直线部分斜率基本不再变化,关联维数趋于饱和(粗实线)。说明正常状态消噪后的振动信号重构相空间最佳嵌入维数为9。
图3(a)为计算获得正常状态下选最佳嵌入维数m=9时对应的K熵结果为0.127 3,作为最终计算结果。用相同方法计算不同故障程度下外圈故障的最佳嵌入维数m及K熵,结果分别见图3(b)、(c)、(d)及表1。由表1看出,故障状态下滚动轴承K熵值均大于正常状态。其中程度2对应K熵值最大。因K熵为描述系统运动混乱或无序程度的物理量,系统K熵值增大时系统运动不确定性亦增大;故障加重到程度3时,由于故障损伤点剥落直径增大导致故障冲击更剧烈,振动能量向故障特征频率处集中,系统运动的确定性增大,故K熵反而开始减小。

图2 正常状态振动信号lnC(r)-lnr曲线Fig.2 lnC(r)-lnr graph of normal bearing vibration signal
表1 不同故障程度下轴承外圈故障K熵值
Tab.1 K entropies of outer ring under different fault degrees

轴承状态延迟时间嵌入维数K熵正常990.1273故障程度13110.4316故障程度24111.2066故障程度33150.3628

图3 不同程度下外圈故障K熵曲线Fig.3 K entropy curves of outer ring under different fault degrees
取长度为1 200点的正常状态数据直接用小波脊线法进行处理,结果见图4。
对轴承正常状态信号进行Hilbert包络解调[14,17],并降低采样频率到2 kHz,获得包络信号的小波脊线见图5。由图5看出,轴承无故障时振动能量主要集中在转轴基频二倍频(58.34 Hz)、四倍频(116.68 Hz)处。
选长度为1 200点程度1的外圈故障数据直接用小波脊线法处理,结果见图6。对比图4、图6知,轴承发生外圈故障时信号表现出明显的冲击特性,且3~4 kHz左右能量明显增大。由图6计算出每两次冲击振动间的平均时间间隔约0.009 52 s,由此得出轴承故障信号中冲击振动频率约105.04 Hz,与轴承外圈故障特征频率104.56 Hz基本一致,说明小波脊线较好反映出信号的真实冲击频率信息。信号在3~4 kHz频段处有能量集中,表明轴承发生外圈故障时其特征主要通过该频率段向外传递,即该频率范围为外圈故障的共振频带。选此频段信号进行带通滤波、包络解调分析可更清楚发现故障特征。


选Daubechies 5小波对消噪后信号进行2层小波包分解,在尺度2上形成4个子频带,各子频段分解系数对应的频率范围见表2。

表2 分解系数对应频带

图7 轴承外圈故障包络信号小波脊线图Fig.7 Wavelet ridges of envelope signal under outer ring fault
由表2看出,小波包系数d(2,2)对应的频带包含轴承外圈故障引起的3~4 kHz共振频带,故选该频段小波系数进行信号重构,可滤去不需要的频率成分实现带通滤波,提取共振频带范围内信号成分。再对d(2,2)系数重构后信号进行Hilbert包络解调,并降低采样频率到2 kHz,提取包络信号的小波脊线,结果见图7(b)、(c)、(d)。为便于对比,将图5重绘,见图7(a)。由图7看出,轴承故障发生时特征频率104.56 Hz处能量集中明显,由此可判定轴承发生外圈故障。轴承处于不同故障程度时小波脊线分布亦不同。处于故障程度2时脊线较混乱,混沌程度最强,具有混沌状态时特有的层次性脊线分布(图7(c));而图7(d)较7(c)表征的混沌程度稍弱,因故障加重到一定程度时,剥落的故障点导致振动加剧,振动信号周期性冲击增强,能量向故障频率处集中,信号的确定性开始增强,混沌程度减弱。与表1中混沌特征量K熵计算结果一致。
2.2 内圈故障振动信号分析
轴承发生内圈故障时的分析方法同前,计算不同故障程度下最佳嵌入维数及K熵,结果见表3。由表3看出,内圈故障状态下轴承的K熵值明显大于正常状态。故障程度1时K熵值最大,随轴承内圈故障程度加重K熵值逐渐降低。

表3 不同故障程度下轴承内圈故障K熵值
选长度1 200点、程度1的内圈故障数据直接用小波脊线法进行处理,结果见图8。对比图4与图8知,轴承发生内圈故障时信号表现出明显的冲击性,且2.3 ~3.7 kHz能量明显增大,说明该频率范围为轴承内圈故障的共振带。由图8计算出每两次冲击振动的时间间隔约0.006 62 s,由此得出轴承故障信号中冲击振动频率约151.06 Hz,与轴承内圈故障特征频率157.94 Hz基本一致。
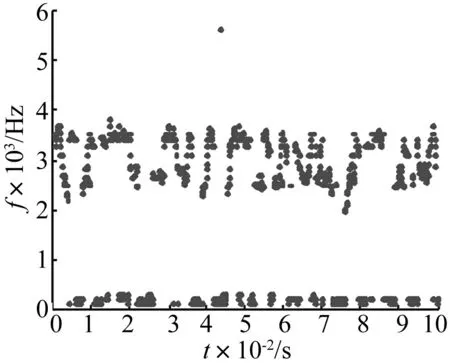
图8 内圈故障小波脊线图Fig.8 Wavelet ridges of inner ring fault
利用小波包分解对信号进行带通滤波,提取内圈故障共振频带2.3 ~3.7 kHz的信号成分进行Hilbert包络解调,并降低采样频率到2 kHz,提取小波脊线,结果见图9。由图9看出,轴承发生故障时在内圈故障特征频率157.94 Hz处能量集中明显,由此可判定轴承发生内圈故障。轴承内圈故障程度不同时小波脊线分布亦不同。轴承处于故障程度1时脊线最混乱(图9(b)),混沌程度最高。随轴承内圈故障程度加重,由于故障造成的冲击振动增强,振动能量向故障特征频率处集中,信号混沌程度减弱,小波脊线分布逐渐清晰。与表3混沌特征量K熵分析结果一致。
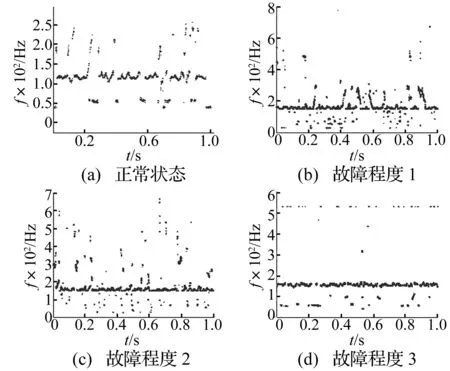
图9 轴承内圈故障包络信号小波脊线图Fig.9 Wavelet ridges of envelope signal under inner ring fault
2.3 滚动体故障振动信号分析
轴承发生滚动体故障时的分析处理方法同外圈故障,所得不同故障程度下最佳嵌入维数及K熵,结果见表4。由表4看出,滚动体故障状态下轴承的K熵值明显大于正常状态。故障程度1时K熵值最大,随轴承滚动体故障程度加重其K熵值逐渐降低。
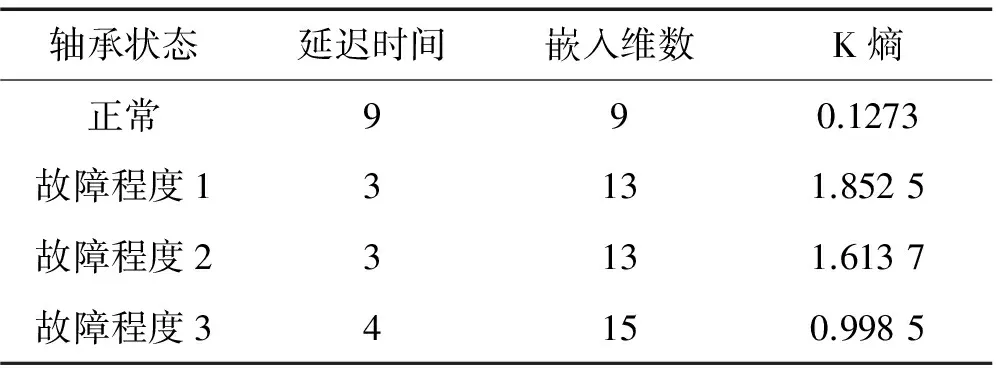
表4 不同故障程度下轴承滚动体故障的K熵值
选长度1 200点、程度1的滚动体故障数据直接用小波脊线法进行处理,结果见图10。由图10看出,轴承发生滚动体故障时振动冲击无明显周期性。因轴承滚动体在运转过程中除正常公转、自转外,还会因轴向力变化引起摇摆及轴向振动。因此轴承滚动体表面存在剥落损伤时,在运动过程中损伤点时而碰到内或外滚道,时而碰不到,导致故障冲击存在随机性,即可能出现故障冲击时有时无或频率时高时低的随机波动现象。因此,滚动体故障状态下其小波脊线图无轴承外圈故障或内圈故障时明显的周期性冲击。

图10 滚动体故障小波脊线图Fig.10 Wavelet ridges of rolling element fault
轴承发生滚动体故障时信号在3 kHz频段处有能量集中,选择此共振频段信号进行小波包带通滤波、包络解调,并提取小波脊线,计算结果见图11。
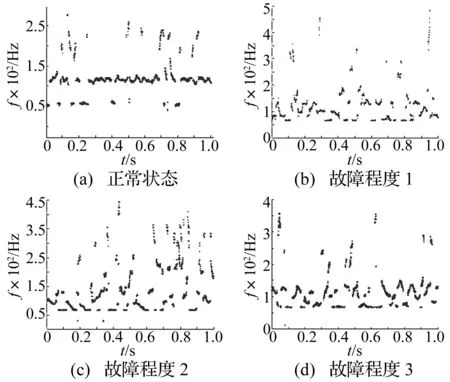
图11 轴承滚动体故障包络信号小波脊线图Fig.11 Wavelet ridges of envelope signal under rolling element fault
由图11看出,轴承发生故障时,在特征频率68.74 Hz及二倍频率137.48 Hz处有较明显的能量集中脊线,由此可判定轴承发生滚动体故障。轴承滚动体故障程度不同时小波脊线分布亦不同。轴承处于故障程度1时脊线图最混乱(图11(b)),混沌程度最高。随轴承滚动体故障程度加重,由于故障造成的冲击振动增强,振动能量向故障特征频率处集中,混沌程度开始减弱,小波脊线亦越清晰。与表4基于混沌特征量K熵计算分析结果一致。
3 结 论
用所提基于小波脊线混沌程度刻画的滚动轴承多故障诊断方法对不同类型、不同程度下轴承故障振动信号进行诊断分析,并计算不同类型、不同程度下的K熵。结论如下:
(1) 轴承发生不同程度故障时表现出不同的混沌程度,K熵能实现轴承故障劣化程度监测,但不同故障类型K熵结果相近,难以实现故障类型识别。
(2) 小波脊线图不仅能根据脊线位置确定故障特征频率,从而准确判定轴承故障类型;且能根据脊线的混沌程度实现故障劣化程度监测。
[1] 张弦, 王宏力. 进化小波消噪方法及其在滚动轴承故障诊断中的应用[J]. 机械工程学报, 2010, 46(15): 76-81. ZHANG Xian, WANG Hong-li. Evolutionary wavelet denoising and its application to ball bearing fault diagnosis [J]. Chinese Journal of Mechanical Engineering, 2010, 46(15): 76-81.
[2] 冯辅周, 司爱威, 饶国强, 等. 基于小波相关排列熵的轴承早期故障诊断技术[J]. 机械工程学报, 2012, 48(13): 73-79. FENG Fu-zhou, SI Ai-wei, RAO Guo-qiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J]. Chinese Journal of Mechanical Engineering, 2012, 48(13): 73-79.
[3] 吴参, 李兴林, 孙守迁, 等. 混沌理论在滚动轴承故障诊断中的应用[J]. 轴承, 2013 (1): 60-64. WU Can, LI Xing-lin, SUN Shou-qian, et al. Application of chaos theory in fault diagnosis of rolling bearings[J]. Bearing, 2013(1): 60-64.
[4] 张景超,张金敏,张淑清,等. 基于小波及非线性预测的轴承故障诊断方法[J].仪器仪表学报,2012, 33(1): 127-131. ZHANG Jing-chao, ZHANG Jin-min, ZHANG Shu-qing, et al. Bearing fault diagnosis method based on wavelet analysis and nonlinear prediction[J]. Chinese Journal of Scientific Instrument, 2012, 33(1): 127-131.
[5] Silva C P, Young A M. Introduction to chaos-based communications and signal processing[C]// Aerospace Conference Proceedings, IEEE, 2000, 1: 279-299.
[6] 姜万录,张淑清,王益群. 混沌运动特征的数值试验分析[J]. 机械工程学报, 2000, 36(10): 13-17. JIANG Wan-lu, ZHANG Shu-qing, WANG Yi-qun. Numerical experimental analysis for chaotic motion characteristics[J]. Chinese Journal of Mechanical Engineering, 2000, 36(10): 13-17.
[7] Jiang Wan-lu. Orthogonal wavelet packet analysis based chaos recognition method[J]. Frontiers of Electrical and Electronic Engineering in China, 2006, 1(1): 13-19.
[8] 秦毅,秦树人,毛永芳. 基于小波脊线的解调方法及其在旋转机械故障诊断中的应用[J].机械工程学报,2009,45(2): 232-242. QIN Yi, QIN Shu-ren, MAO Yong-fang. Demodulation approach based on wavelet ridge and its application in fault diagnosis of rotating machinery[J]. Chinese Journal of Mechanical Engineering, 2009, 45(2): 232-242.
[9] 朱洪俊,王忠. 小波变换对瞬态信号特征信息的精确提取[J]. 机械工程学报, 2005, 41(12): 196-199. ZHU Hong-jun, WANG Zhong. Accurate extraction for the characteristic information of transient sigal with wavelet transforms[J]. Chinese Journal of Mechanical Engineering, 2005, 41(12): 196-199.
[10] Delprat N, Escudie B, Guillemain P, et al. Asymptotic wavelet and gabor analysis: extraction of instantaneous frequencies[J]. IEEE Transactions on Information Theory, 1992, 38(2): 644-664.
[11] Carmona R A, Hwang W L, Torresani B. Characterization of signals by the ridges of their wavelet transforms[J]. IEEE Transactions on Signal Processing, 1997, 45(10): 2586-2590.
[12] Mallat S. A wavelet tour of signal processing (3rd)[M]. Burlington:Academic Press, 2009: 89-134.
[13] The case western reserve university bearing data center. Bearing data center fault test data[EB/OL]. http://www. eecs.cwru.edu/laboratory/bearing,201l.
[14] Jiang W L, Spurgeon S K, Twiddle J A, et al. A wavelet cluster-based band-pass filtering and envelope demodulation approach with application to fault diagnosis in a dry vacuum pump[J]. Journal of Mechanical Engineering Science, 2007, 221(11): 1279-1286.
[15] 姜万录,陈东宁,姚成玉.关联维数分析方法及其在液压泵故障诊断中的应用[J].传感技术学报,2004,17(1): 62-65. JIANG Wan-lu, CHEN Dong-ning, YAO Cheng-yu. Coorelation dimension analytical method and its application in fault diagnosis of hydraulic pump[J]. Sensors and Actuators,2004, 17(1): 62-65.
[16] Craig C, Neilson R D, Penman J. The use of correlation dimension in condition monitoring of systems with clearance[J]. Journal of Sound and Vibration, 2000, 231(1): 1-17.
[17] 张进, 冯志鹏, 褚福磊. 滚动轴承故障特征的时间-小波能量谱提取方法[J]. 机械工程学报, 2011, 47(17): 44-49. ZHANG Jin, FENG Zhi-peng, CHU Fu-lei. Extraction of rolling bearing fault feature based on time-wavelet energy spectrum[J]. Chinese Journal of Mechanical Engineering, 2011, 47(17): 44-49.
Wavelet ridges-based fault diagnosis for rolling bearings
JIANG Wan-lu1, 2, LI Ning-ning1, 2, ZHU Yong1, 2
1. Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control, Yanshan University, Qinhuangdao 066004, China;2. Key Laboratory of Advanced Forging & Stamping Technology and Science, Ministry of Education of China, Yanshan University, Qinhuangdao 066004, China)
There are abundant nonlinear dynamic characteristics appearing in vibration signals when faults happen on rolling bearings. According to the advantages of wavelet ridges in analyzing nonlinear and non-stationary signals, a novel method for the chaotic degree depiction based on wavelet ridges was proposed. And it was applied to diagnose multi-type faults of rolling bearings. The wavelet ridges were extracted from the envelope signal in the resonance vibration frequency band of fault vibration signals. Moreover, the Kolmogorov entropies were calculated from the fault vibration signals of rolling bearings in order to compare with the wavelet ridges. The results indicate that the wavelet ridges not only can identify the fault types of rolling bearings, but also can reflect the severity degrees of the faults by means of the chaotic degrees depiction.
chaotic degree depiction; wavelet ridge; Kolmogorov entropy; fault diagnosis; rolling bearing
国家重点基础研究发展 (973) 计划资助项目(2014CB046405);河北省自然科学基金资助项目(E2013203161);国家自然科学基金资助项目(51075349)
2014-04-17 修改稿收到日期:2014-07-30
姜万录 男,博士,教授,博士生导师,1964年11月生
TH137;TP277
A
10.13465/j.cnki.jvs.2015.14.001

