柔性基础上金属橡胶隔振系统混沌响应研究
李玉龙, 白鸿柏, 何忠波
军械工程学院, 石家庄 050003)
柔性基础上金属橡胶隔振系统混沌响应研究
李玉龙, 白鸿柏, 何忠波
军械工程学院, 石家庄 050003)
研究柔性基础上金属橡胶隔振系统混沌响应。通过对柔性基础等效简化,将整个系统简化为双层线性-非线性混合隔振系统建立数学模型,给出状态方程;对给定的隔振系统参数进行数值仿真分析,绘制系统响应随激励幅值、频率变化分岔图。通过对不同参数下系统时间历程曲线、相轨迹图、庞加莱映射图及频谱图分析,确定系统产生混沌响应的参数取值;并实例讨论金属橡胶隔振系统混沌振动应用的一般方法,为柔性基础上金属橡胶非线性系统混沌振动的应用奠定基础。
金属橡胶;非线性隔振系统;柔性基础;混沌
金属橡胶(Metal Rubber)为经特殊工艺制成的弹性多孔金属材料,既呈现类似橡胶材料的弹性、阻尼性能,又保持金属的优异特性,为具有重要工程应用价值的非线性结构功能材料[1]。其隔振系统除具有耐高温、高压、高真空、超低温,在空间环境下不挥发、不怕辐射及粒子撞击等优点外,亦具有变刚度、变阻尼的非线性特性。变刚度特性既能使系统自动避开共振点,又能确保系统在突变的冲击载荷下仍有一定隔振抗冲击性能保护设备不被损坏;变阻尼特性既能有效降低共振区内振动传递率,又能在隔振区内保证系统具有较好振动衰减效果[2]。因此,金属橡胶广泛用于航空航天、船舰、车辆等隔振系统,对提高装备寿命及可靠性至关重要。
金属橡胶隔振系统为典型的迟滞非线性系统,对其已有诸多建模、理论及试验研究[2-5],为推广应用奠定理论基础。由于混沌为非线性系统特有运动形式,金属橡胶隔振系统必会产生混沌,但对其研究成果较少,仅有文献[6]利用系统一次谐波解推导出金属橡胶隔振系统产生混沌振动的解析条件。研究金属橡胶隔振系统的混沌特性可借鉴其它非线性隔振系统研究成果。叶建军等[7]研究含二、三次非线性项系统的次谐轨道及异宿轨道;楼京俊等[8]研究多频激励软弹簧型Duffing系统中的混沌运动;唐果等[9]研究单自由度被动隔振体产生混沌的参数条件;刘树勇等[10]用Melnikov方法确定准周期激励下非线性隔振系统的混沌参数区域;Yu等[11]研究多自由度非线性隔振系统的混沌及分岔;黄志伟等[12]分析双层隔振系统产生混沌的频率范围。浣石等[13-17]认为混沌状态系统具有单频输入宽频输出特性,可大幅度隔离结构噪声中线谱成分,具有消除线谱激励的明显优势,对提高舰船的隐身性能具有重要意义。
随轻薄化板壳结构在现代装备工程尤其舰船领域的广泛应用,装备非刚性基座结构振动产生的辐射噪声愈加严重,须考虑柔性基础与被隔振设备振动的耦合问题。而对柔性基础上金属橡胶隔振系统混沌研究尚少见。本文拟对柔性基础上金属橡胶非线性隔振系统的混沌展开研究,主要通过数值仿真获得系统产生混沌运动的参数取值条件,证明柔性基础上金属橡胶非线性隔振系统能产生混沌振动,为工程中需避开有害混沌振动,进行金属橡胶隔振设计提供理论参考;为提高船舰隐身性能,改变振动噪声辐射线谱成分,设计能产生混沌振动的金属橡胶隔振系统需求奠定理论基础。
1 柔性基础上金属橡胶隔振系统模型
图1(a)为含柔性基础的金属橡胶隔振系统,刚性设备通过金属橡胶隔振器支撑安装于柔性基础上。为简化分析,以两边简支矩形薄板模拟柔性基础,对模型作假设为:① 刚性设备被一单向金属橡胶隔振器支撑;② 只考虑竖直向振动,激励作用于刚性设备质心,沿竖直向做简谐激励,且F(t)=F0cos(ΩT);③ 两边简支基础板等效成线性单自由度质量-弹簧-阻尼系统。因此,将系统转化为两层的隔振模型,见图1(b)。
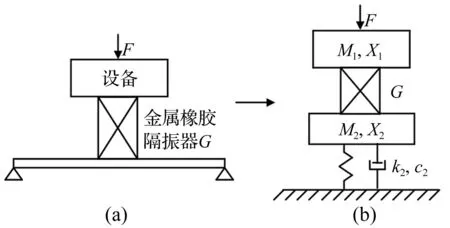
图1 柔性基础上金属橡胶隔振系统模型Fig.1 Model of metal rubber vibration isolation system onflexible foundation
图1(b)中M1,M2分别为被隔振设备质量、基础板等效质量;x1,x2为各自位移;k2,c2为基础等效刚度、等效阻尼;G为金属橡胶隔振器,用双折线泛函本构关系模型表示[2-3,18]为
(1)
式中:y(t)为隔振器变形量;k01为一次线性刚度系数;k3为三次非线性刚度系数;c01为粘弹阻尼系数;c3为三次非线性粘弹阻尼系数,其形成与位移有关的弹性力及与速度有关的粘性阻尼力被认为无记忆恢复力;z(t)为金属橡胶变形中干摩擦引起的记忆恢复力;zs为滑移极限;ks为滑移刚度,ks=zs/ys。
将记忆恢复力用双折线模型表示,见图2。其中ys为开始滑移时变形;ym为最大变形量。

图2 双折线迟滞关系模型Fig.2 Double broken linear hysteresis model
为简化分析,用等效线性化法对干摩擦滞迟环节进行等效线性化[18],得

(2)
将记忆环节进行线性等效,即包含变化的刚度项keq及变化的粘性阻尼项ceq。由keq,ceq表达式看出,二者仅与每次往复的最大变形量ym有关,对正弦加载的振动系统,ym等于振动幅值,且保持不变。金属橡胶隔振器在隔振系统中的力-位移关系可写为
(3)
式中:k1=k01+keq;c1=c01+ceq。
图1(b)两自由度金属橡胶非线性隔振系统微分方程可写为
(4)
(5)
(6)
据式(5)、(6),方程(4)可写为
(7)
(8)
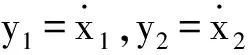
(9)
2 隔振系统数值响应分析
为研究金属橡胶隔振系统的混沌响应,先对方程组(9)的系数赋值,定义无量纲参数ξ1=0.15,ξ2=0.8,μ=5,β=100,设ω=1.18,f=1~50,步长Δf=0.1,x1,x2,y1,y2初始值均为0。用四阶龙格-库塔法求解动力学微分方程,获得系统随激励幅值f变化分岔图,见图3。由图3看出,激励力频率ω=1.18时质量块1、2的响应均多次出现分岔现象,且幅值在15~25范围内出现混沌振动。
为获得系统出现混沌的激励频率区间,选f=16,ω=0~5,步长Δω=0.01,其它无量纲参数及初始条件不变,用四阶龙格-库塔法求解动力学微分方程,获得系统随激励频率ω变化分岔图,见图4。由图4看出,激励幅值f=16时系统在激励频率ω=0.4~0.6及ω=0.95~1.2内可能出现混沌振动。
为验证参数区间的准确性,令f=16,ω=1.18、ω=3.1、ω=4.8,其它参数及初始条件均不变,求得系统响应的时间历程曲线、相轨迹、Poincare映射图及频谱图见图5。由图5(a)看出,激励频率参数f=16及ω=1.18时,质量块1、2的时域波形较混乱,周期振动曲线不稳定;相图显示该运动为往复的、有限的且周期是无限长的运动;庞加莱映射图既不是有限点集,也不是封闭曲线;频谱图显示,响应中有多种频率成分,且频谱几乎连续。在该参数条件下,隔振系统的两质量块均处于混沌运动状态。由图5(b)、(c)的时域波形看出,质量块响应经一段时间后趋于稳定;其相图显示为往复运动,且有确定周期;庞加莱映射图为封闭曲线,故运动为准周期的;频谱图显示频率成分较单一。故ω=3.1及ω=4.8时,质量块1、2均为准周期振动。


由分析结果知,参数ξ1=0.15,ξ2=0.8,μ=5,β=100,ω=1.18,f=16时,系统处于混沌振动状态。因混沌运动对初始条件有敏感性,将初始条件进行微小差异设定,即[0 0 0 0]、[0 0 0.1 0.1],用四阶龙格库塔法求解系统时域响应曲线并对比,见图6。由图6看出,初始条件变化时系统的时间历程曲线随时间推移发生较大变化,证明在给定参数条件下,该系统响应对初始状态较敏感,表明在给定参数条件下系统两质量块均处于混沌运动状态。
3 混沌振动应用实例分析
对柔性基础与隔振器已定的隔振系统,设质量分别为M1=20 kg,M2=5 kg,为获得隔振器各参数,对其进行2 mm、5 Hz的正弦加载试验,见图7(a)。用遗传算法对动态试验数据进行参数识别[19],得隔振器各参数识别结果为k01=133.5 N/mm、k3=14.9 N/mm3、c01=1.9 N/(mm/s)、zs=88.2 N、ys=0.8 mm、ks=107.7 N/mm。利用辨识参数结果绘制曲线与试验曲线对比见图7(b)。
结合式(2)得ceq=6.7 N/(mm/s)、keq=15.0 N/mm。因此得c1=8.6 N/(mm/s)、k1=148.5 N/mm。设柔性基础的等效刚度、阻尼分别为k2=10 000 N/mm、c2=10 N/(mm/s)。结合式(8),得式(9)中无量纲参数为ξ1=0.158,ξ2=0.735,β=67.3,μ=4,ω1n=2.7。据第2节分析,讨论系统产生混沌运动时的无量纲激励力幅值、频率参数f及ω取值分别为f=10.8,ω=1.95。
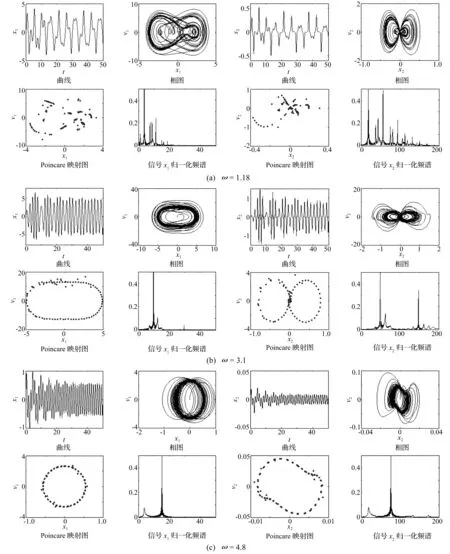
图5 系统时域波形、相轨迹、Poincare映射及频谱图Fig.5 Poincare maps, phase, time-histories and amplitude spectrum diagrams of the system response
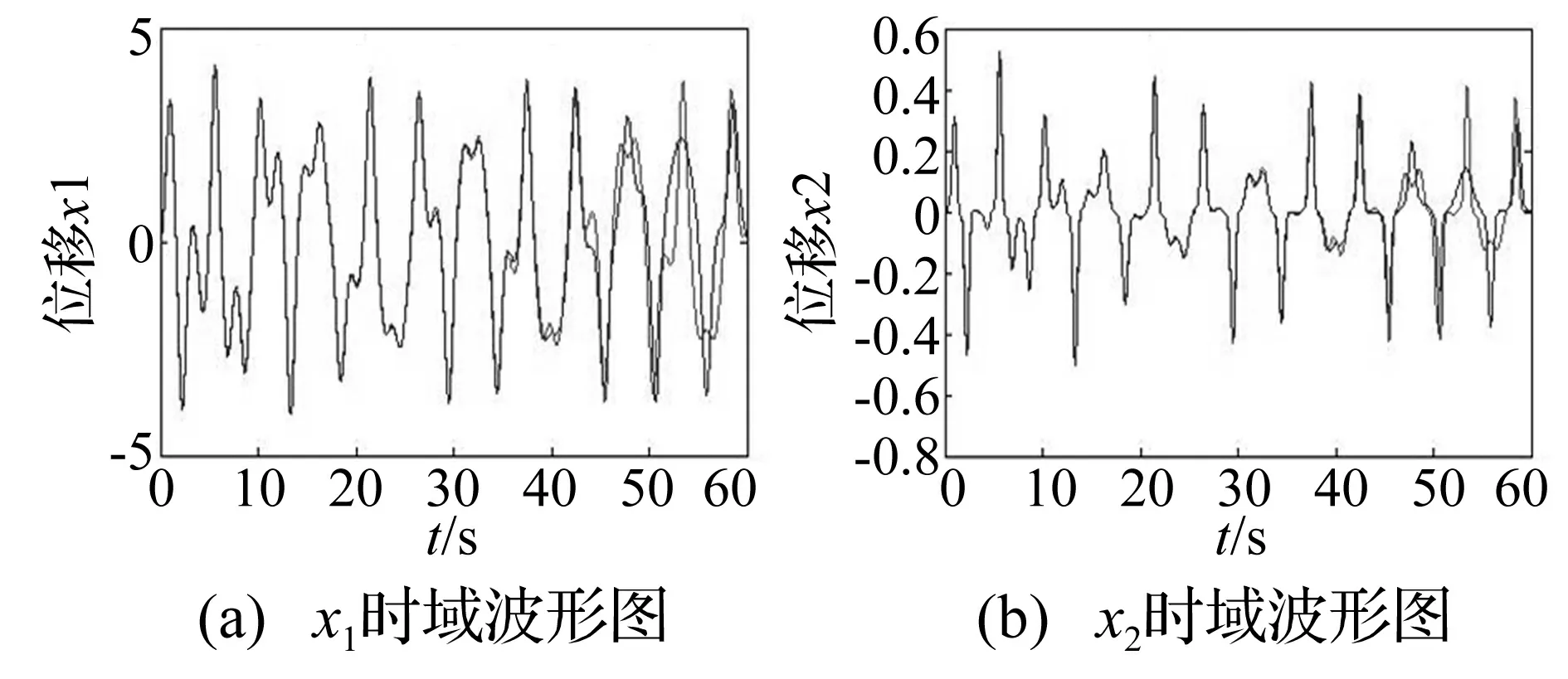
图6 不同初始条件下系统响应的时域波形图Fig.6 Time-histories diagrams of different initial conditions
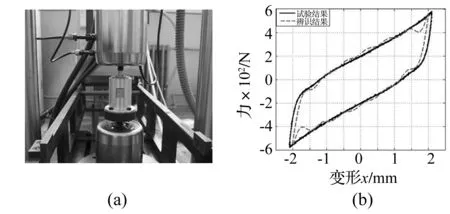
图7 试验装置与结果对照Fig.7 Dynamic experimentpicture and the compared test curve result and the parameter identification result
由式(8)得
(10)
由式(10)得F0=5 063 N,Ω=5.3 rad/s,即确定隔振系统在激励力5 063 N圆频率5.3 rad/s时产生混沌。
将实际物理参数值代入式(4),并令x1,x2,y1,y2的初始值分别为[0 0 0 0]及[0 0 0.1 0.1],用四阶龙格-库塔法求解,获得实际物理参数下系统时域响应曲线及相轨迹见图8。由图8看出,被隔振设备与柔性基础的时域波形较混乱,周期振动曲线不稳定,且随时间推移,微小初值对系统响应影响较大;被隔振设备及柔性基础的相轨迹均为往复、有限且周期无限长的运动,可见系统此时处于混沌振动状态。

图8 物理参数下系统时域、相轨迹图Fig.8 Time-histories diagrams and phase under the physical parameter
以上主要针对确定参数的金属橡胶隔振系统,研究激励幅值、频率变化导致隔振系统产生混沌的参数区间,可在工程实际中调整激励幅值及频率参数,使系统处于混沌振动状态达到改变系统振动线谱成分目的;也可通过避开该参数取值防止有害混沌振动产生。
对确定激励环境下金属橡胶隔振系统设计问题,仍可按本文思路讨论系统本身参数,即先确定无量纲激励幅值f及频率ω,对其它无量纲参数ξ1,ξ2,β,μ逐一讨论,分别绘制隔振系统随单个无量纲参数变化分岔图,综合分析确定ξ1,ξ2,β,μ的取值区间,结合式(8)即可求得系统本身的有量纲参数取值区间;再据有量纲系统参数取值区间设计金属橡胶隔振器,并进行动态试验验证系统的混沌响应。
需指出,由于金属橡胶加工制备工艺限制,难以直接设计出准确参数元件,因此,需对金属橡胶隔振器进行静、动态试验,不断调整加工制备参数,以确定隔振器参数满足设计要求。由于混沌响应只在特定参数区间产生,对组装好的系统仍需大量试验验证。
4 结 论
通过对柔性基础上金属橡胶隔振系统的混沌响应特性研究,提出将系统混沌用于指导工程实际一般分析方法,结论如下:
(1) 建立隔振系统简化模型,将柔性基础等效为单自由度弹簧阻尼系统,使系统简化为两层线性-非线性混合隔振系统,建立数学模型,给出状态方程。
(2) 对给定隔振系统无量纲参数进行数值仿真分析,绘制系统激励幅值f及频率ω参数变化分岔图,获得系统响应产生多次分岔的激励幅值及频率取值区间,通过对不同参数下系统的时间历程曲线、相轨迹、庞加莱映射及频谱图分析,确定系统产生混沌响应的参数取值。通过对混沌系统对初始条件敏感性对比分析表明,柔性基础上金属橡胶隔振系统能产生混沌运动。
(3) 通过混沌工程应用实例分析,获得系统产生混沌时激励的实际物理参数取值,并通过数值求解所得系统时域响应曲线、相轨迹图验证实例计算所得物理参数下系统处于混沌振动,证明本文理论推导的正确性。
(4) 由于金属橡胶隔振系统复杂性,理论分析仅有一定指导意义,实际工程应用中仍需辅以大量试验研究,才能获得设计目标要求的柔性基础上金属橡胶混沌振动系统。
[1] 李玉龙,何忠波,白鸿柏,等.金属橡胶的研究及应用研究[J].兵器材料科学与工程,2011,34 (1):103-108. LI Yu-long, HE Zhong-bo, BAI Hong-bai, et al. Advance in research and application of metal rubber[J]. Ordnance Material Science and Engineering,2011,34 (1):103-108.
[2] 白鸿柏,路纯红,曹凤利,等.金属橡胶材料及工程应用[M].北京:科学出版社,2014.
[3] 李宇明,郑坚,白鸿柏. 金属橡胶材料的动态力学模型[J]. 材料研究学报,2003,17(5):499-504. LI Yu-ming, ZHENG Jian, BAI Hong-bai. Dynamic mechanics model of metal-rubber materials[J]. Chinese Journal of Materials Research, 2003,17(5):499-504.
[4] 许建东,郭宝亭,朱梓根,等.金属橡胶材料的振动特性[J]. 航空动力学报,2004,19(5):619-622. XU Jian-dong, GUO Bao-ting, ZHU Zi-gen,et al. The vibration performance of metal-rubber material[J]. Journal of Aerospace Power, 2004, 19(5): 619-622.
[5] 高永毅,陈安华,郭源君.金属橡胶隔振器的非线性动力学[J].中国有色金属学报,2009,19(12):2216-2221. GAO Yong-yi, CHEN An-hua, GUO Yuan-jun. Nonlinear dynamics of metal rubber danper[J]. The Chinese Journal of Nonferrous Metals, 2009,19(12):2216-2221.
[6] 唐果,陈安华,郭源君.金属橡胶隔振器产生混沌的解析预测[J]. 航空动力学报,2012,27(8):1752-1757. TANG Guo, CHEN An-hua, GUO Yuan-jun. Chaotic prediction of metal rubber damper for occurred chaos[J]. Journal of Aerospace Power, 2012,27(8):1752-1757.
[7] 叶建军,陈虬.一类非线性振动系统的混沌运动[J].西南交通大学学报,2001,36(6):629-632. YE Jian-jun, CHEN Qiu. Chaotic motions in nonlinear vibration systems[J]. Journal of Southwest Jiaotong University, 2001,36(6): 29-632.
[8] 楼京俊,何其伟,朱石坚.多频激励软弹簧型Duffing系统中的混沌[J].应用力学和数学,2004,25(12):1300-1304. LOU Jing-jun, HE Qi-wei, ZHU Shi-jian. Chaos in the softening duffing system under multi-frequency periodic forces [J]. Applied Mathematics and Mechanics, 2004,25(12): 1300-1304.
[9] 唐果,陈安华,郭源君.被动隔振体产生混沌的参数条件研究[J].振动与冲击,2010,29(8):35-39. TANG Guo, CHEN An-hua, GUO Yuan-jun. Parametrical condition for chaos occurrence on a vibration-isolated body[J]. Journal of Vibration and Shock,2010, 29(8):35-39.
[10] 刘树勇,朱石坚,俞翔.准周期激励非线性隔振系统的混沌研究[J].船舶力学,2010,14(2):141-147.
LIU Shu-yong, ZHU Shi-jian, YU Xiang. Study on the chaos of the nonlinear vibra tion isolation system under quasi-periodic excitation[J]. Journal of Ship Mechanics, 2010,14(2): 141-147.
[11] Yu Xiang, Zhu Shi-jian, Liu Shu-yong. Bifurcation and chaos in multi-degree-of-freedom nonlinear vibration isolation system [J]. Chaos, Solitons & Fractals,2008,385(5):1498-1504.
[12] 黄志伟,何雪松,陈志刚,等.非线性隔振系统振动特性分析[J]. 动力学与控制学报,2013,11(3):252-256. HUANG Zhi-wei, HE Xue-song, CHNE Zhi-gang.et al. Research on the vibration characteristics of nonlinear isolation system[J]. Journal of Dynamics and control,2013,11(3): 252-256.
[13] 浣石,陶为俊,朱石坚,等. 硬特性隔振装置混动动力学特性研究[J].振动与冲击,2011,30(1):245-248. HUAN Shi, TAO Wei-jun, ZHU Shi-jian, et al.Chaotic dynamic of harding nonlinear isolation device[J]. Journal of Vibration and Shock, 2011,30(1):245-248.
[14] 徐道临,吕永建,周加喜,等.非线性隔振系统动力学特性分析的FFT多谐波平衡法[J]. 振动与冲击,2012,31(22): 39-44. XU Dao-lin, LÜ Yong-jian, ZHOU Jia-xi, et al. FFT multi-harmonic balance method for dynamic analysis of a nonlinear vibration isolation system[J]. Journal Vibration and Shock, 2012, 31(22): 39-44.
[15] 谢向荣,朱石坚.船舶动力机械双层混合隔振系统非线性动力学特性研究[J].振动与冲击,2010,29(3):174-177. XIE Xiang-rong, ZHU Shi-jian. Study on the nonlinear dynamics of the two-stage hybrid isolation system of power machinery on ships[J]. Journal of Vibration and Shock, 2010, 29(3):174-177.
[16] 段小帅,梁青,陈绍青,等.双层隔振系统隔振效果评价与试验[J].振动、测试与诊断,2010,30(6):694-697. DUAN Xiao-shuai, LIANG Qing, CHEN Shao-qing, et al. Evaluation and experiment on-vibration-isolation effect of double-stage vibration isolation system[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(6):694-697.
[17] 高书磊,霍睿. 柔性基础上非线性隔振系统的动力学分析[J].振动与冲击,2007,26(6):113-115. GAO Shu-lei, HUO Rui. Effect of nonlinear parameter of isolator on equipment’s kinetic energy[J]. Journal of Vibration and Shock, 2007,26(6): 113-115.
[18] 白鸿柏,张培林,郑坚,等.迟滞振动系统及其工程应用[M]. 北京:科学出版社,2002.
[19] Li Yu-long, Bai Hong-bai, He Zhong-bo. Parameter identification of a new metal rubber damper system[J]. Applied Mechanics and Material, 2014,528:54-60.
Chaotic response of metal rubber vibration isolation system on flexible foundation
LI Yu-long, BAI Hong-bai, HE Zhong-bo
Ordnance Engineering College, Shijiazhuang 050003, China)
A metal rubber vibration isolation system was simplified as a two-stage linear-nonlinear vibration isolation system through the equivalent simplification of its flexible foundation. The mathematical model of the system was built, and the state equation was derived. Then the numerical simulation of the system was provided with the Runge-Kutta method and the bifurcation diagrams in terms of excitation force and frequency were obtained. The parameters of the system related to the of arising of chaotic response were identified by the analysis of the time-history, phase trace, poincare map and amplitude spectrum diagrams of the system with different parameters. The general application of the chaotic vibration of metal rubber vibration isolation system was discussed by using a practical example.
metal rubber; nonlinear vibration isolation system; flexible foundation; chaos
武器装备“十二五”预先研究项目(51312060404)
2014-08-20 修改稿收到日期:2014-12-13
李玉龙 男,博士生,1981年5月生
白鸿柏 男,教授,博士生导师,1964年生
TB533;O322
A
10.13465/j.cnki.jvs.2015.14.017

