基于PMCMC-RFS的自主车SLAM算法

苏奎峰， 常天庆， 张 雷， 杨国振

(装甲兵工程学院控制工程系， 北京 100072)

基于PMCMC-RFS的自主车SLAM算法

苏奎峰， 常天庆， 张 雷， 杨国振

(装甲兵工程学院控制工程系， 北京 100072)

针对无人自主车同时定位与地图构建(Simultaneous Localization And Mapping，SLAM)问题，采用随机有限集(Random Finite Set, RFS)方法对环境特征和车辆的位姿进行描述，将SLAM算法涉及到的多路标特征检测、跟踪、识别及相关等问题在一个统一的贝叶斯状态估计框架内表述，从而可以有效地解决后验估计、信息融合等算法严重依赖数据关联结果的问题。同时，为了计算复杂的联合后验分布，解决粒子滤波算法中提议分布选择困难问题，采用序贯蒙特卡罗(Sequential Monte Carlo，SMC)算法为马尔科夫链蒙特卡罗(Markov Chain Monte Carlo，MCMC)采样构建高维提议分布策略，提出了基于PMCMC-RFS(Particle MCMC based RFS)的SLAM问题求解方法。试验结果表明：PMCMC-RFS算法能动态估计感知范围内的特征数量，有效地避免了数据关联问题，从而提高了状态估计性能。

同时定位与地图构建；随机有限集；马尔科夫链蒙特卡罗；粒子滤波

同时定位与地图构建(Simultaneous Localization And Mapping，SLAM)最早由Smith等[1]作为统计状态估计问题而提出，是指无人平台或机器人在未知环境行驶过程中逐步构建环境地图的同时估计自身的位姿状态，是无人自主车辆的关键技术，是环境感知、路径规划、避障以及运动控制的基础。因SLAM具有重要的理论和应用价值，被众多学者认为是移动机器人实现完全自主行驶的关键技术，已成为机器人领域研究的热点之一。

经典SLAM问题采用空间矢量方法描述自主车和路标状态，需要独立估计路标特征、数量以及自主车位姿状态，状态估计结果严重依赖数据关联结果，且对其不确定性非常敏感。此类SLAM算法的主要问题在于：没有将数据关联、状态估计的不确定性集成在统一的贝叶斯框架内考虑，而且在状态估计阶段又假设数据关联结果已知，从而导致算法的环境适应能力和鲁棒性较差。在SLAM 问题中，地图特征实质上是有限集合，采用随机有限集(Random Finite Set，RFS)理论描述和处理此类问题更为合理。将地图特征对应的多路标状态和传感器观测信息表示成RFS，对自主车位姿和地图特征联合后验概率密度分布进行递推贝叶斯估计，进而能够有效描述多种不确定因素的同时，避免了复杂的多目标数据关联问题，解决了复杂环境下路标特征数量不确定的多特征跟踪问题[2-3]。

采用RFS理论可将多传感器信息融合的多路标检测、跟踪、识别以及相关等问题统一起来，能够有效处理后验估计、信息融合算法评估等问题。本文针对路标特征密集、动态特征较多的城乡道路环境，采用RFS理论构建了RFS-SLAM模型，并将SLAM路标估计问题转换为多路标跟踪问题，给出了基于粒子滤波概率密度假设的RFS-SLAM求解方法。为计算复杂的联合后验分布，解决粒子滤波算法中提议分布选择困难问题，采用序贯蒙特卡罗(Sequential Monte Carlo，SMC)算法为马尔科夫链蒙特卡罗(Markov Chain Monte Carlo，MCMC)采样设计高维提议分布，使得可以从SMC或MCMC不能单独采样的高维概率分布密度函数中采样，进而提出了基于PMCMC-RFS(Particle MCMC based RFS) 的SLAM问题求解方法。最后，通过无人自主车现场试验对相应的算法性能进行了分析验证。

1 基于RFS的SLAM模型

(1)

测量信息yk的集合表示为

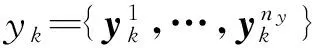
(2)

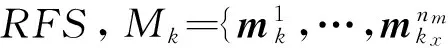
Mk=Mk-1∩C(x0:k-1),

(3)

式中：C(x0:k-1)=C(x0)∪C(x1)∪…∪C(xk-1)。因此，Mk-1就表示k-1时刻之前每个时刻观测特征空间的并集，则遍历过程地图或特征更新的方程为

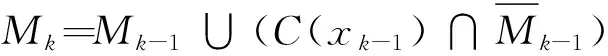
(4)

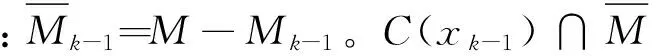
(5)

式中：fM(w|Mk-1)为k-1到k时刻检测范围内特征集合的转移密度；fB(Mk-w|xk)为k时刻进入检测范围内新特征Bk(xk)的密度。

同时,可以采用标准马尔科夫模型对自主车动力学系统进行建模，转移密度表示为fx(xk|xk-1,uk)，uk为控制输入。则k时刻自主车位姿和地图的联合转移密度为

fk|k-1(Mk,xk|Mk-1,xk-1,uk)=

fM(Mk|Mk-1,xk)fx(xk|xk-1,uk)，

(6)

k时刻的量测信息描述为

(7)

式中：Mk(m,xk)为特征m产生的测量RFS;Sk(xk)为k时刻的误检，与当前自主车的位姿xk有关。

yk由ny个随机测量组成，ny也是随机的，其出现的次序相对估计的特征地图没有任何物理意义。特征m产生的测量RFS可以采用Bernoulli分布对RFS进行模型化:

g(yk,xk)=

(8)

对于给定自主车位姿xk，pM(m,xk)为检测到特征m的概率;一旦检测到特征，gk(yk|xk,Mk)就是在m处产生测量yk相对应的似然。根据随机集合统计理论，测量似然

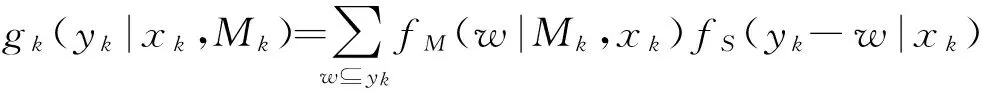
(9)

式中:fM(w|Mk,xk)为观测有限集的密度;fS(yk-w|xk)为误检RFS的密度。

由此可见:似然中直接包含了固有的测量不确定性，fM(w|Mk,xk)也综合了检测不确定量和测量噪声。

令地图Mk和车辆轨迹x1:k的联合后验密度为pk(Mk,x1:k|y1:k,u1:k,x0)，静态地图的递归更新为

pk|k-1(Mk,x1:k)=fx(xk|xk-1,uk)×

∫fM(Mk|Mk-1,xk)×

pk-1(Mk-1,x1:k-1)δMk-1,

(10)

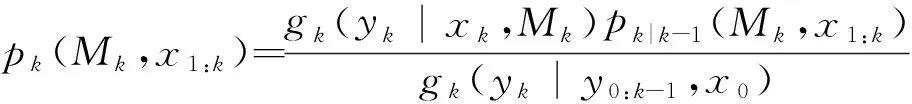
(11)

式中:gk(yk|y0:k-1,x0)=∬gk(yk|Mk,xk)pk|k-1(Mk,xk|y1:k-1,u1:k,x0)δxkδMk，δ表示集合积分。

联合后验密度涵盖了所有地图和自主车位姿的统计信息，可以根据截止到k时刻的测量和控制历史进行推理。RFS-SLAM算法将数据关联和特征数量的不确定性集成到一个单一的贝叶斯滤波器中，不需要独立的数据关联操作和相应的特征管理。RFS-SLAM的联合后验估计等价于轨迹的后验密度估计和基于轨迹的地图后验估计，即

pk|k-1(Mk|x0:k)= ∫fM(Mk|Mk-1,xk)×

pk-1(Mk-1,x1:k-1)δMk-1,

(12)

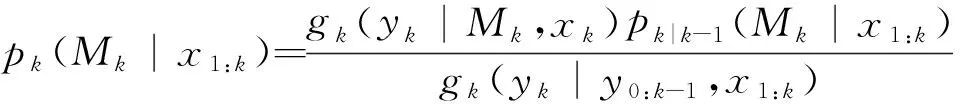
(13)

pk(x1:k)=

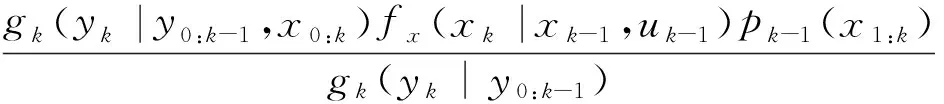
(14)

除了采用测量和地图的随机有限集似然外，由式(12)-(14)确定的RFS-SLAM递归贝叶斯估计模型算法与EKF-FastSLAM[4]算法类似。但EKF-FastSLAM算法将式(14)进一步分解成np个独立的密度函数，其中np为地图中特征的个数，首先完成数据相关和特征数量估计，然后采用独立的估计器对地图进行传递和更新。相比较而言，RFS-SLAM采用RFS的形式描述，地图信息传递采用RFS表示，不依赖数据关联和特征数量估计的结果。

2 基于粒子滤波的RFS-SLAM算法

2.1 RFS-SLAM算法描述

式 (12)给出的RFS-SLAM后验密度计算涉及到多个集合积分的计算问题，相对单一状态估计而言，计算复杂度非常高。SMC采用加权的随机采样近似后验分布[5-6]，能够实现后验密度的递归估计。RFS的置信度在某种意义上就是RFS的概率密度[7]，其采样和近似方法与概率密度函数基本相同。单路标特征粒子滤波算法可以直接应用于多路标特征情况，只是多路标特征的粒子是有限集合，本身维数也可能是变化的。

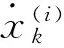
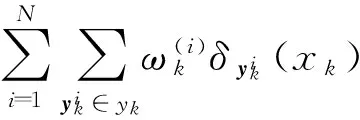
(15)

1) 预测

(1) 采样

(16)

式中：Jk为新产生的粒子数，可以选择状态转移密度函数fk|k-1(ζk|ζk-1,uk,yk)作为重要性采样密度函数；pk(·|yk)表示新特征在传感器感知范围内出现的概率密度函数，根据自主车位姿状态转移和传感器测量特征，采用混合高斯模型给出先验信息。

(2) 计算预测粒子权重

(17)

2) 更新

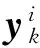
(18)

(2) 对i=1,…,Nk-1+Jk更新权重

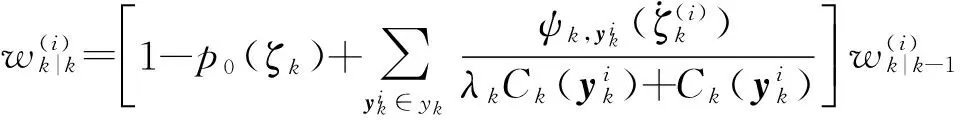
(19)

3) 重采样

4) 状态估计

2.2 基于PMCMC的RFS-SLAM问题求解

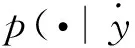
当特征测量集合或目标状态数较大时， RFS递归贝叶斯后验公式中的似然很难计算，从而限制了MCMC算法对后验分布的直接近似。为此，通过引入中间变量的方法采用给出的似然描述方式进行计算，即

(20)

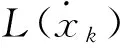
(21)

式中:κk为k时刻的噪声干扰强度；u,v=∫u(t)v(t)dt。

ω(θk) =e。

(22)

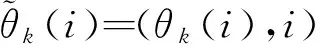
(23)

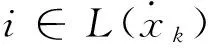
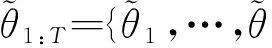
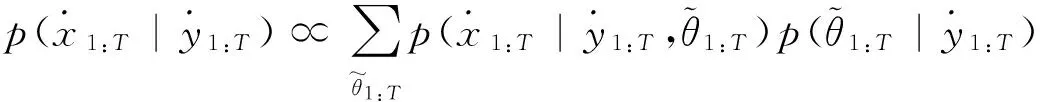
(24)

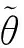
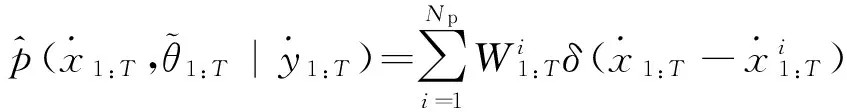
(25)

式中：Np为采样粒子数。

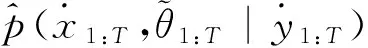
3 算法验证

首先选用如图1所示的仿真测试环境，其中车辆的参考轨迹利用自主车DGPS-RTK模式测量得到，行驶距离、航向角变化等数据根据实车测量得到并加注时间标签，以便在仿真试验时方便对准时间。路标点则采用人工设置，并假定传感器的探测距离为15 m，感知角度为360°。FastSLAM算法采用独立的特征管理操作处理数据关联问题，RFS-SLAM算法则将特征管理、数据关联和状态估计集成在一个统一的贝叶斯更新框架内。

图1 测试环境地图和车辆轨迹

采用EKF-FastSLAM和PMCMC-RFS-SLAM算法估计的东向和北向误差分别如图2、3所示，其中：EKF-FastSLAM算法采用最近邻算法处理相关问题，且根据传感器的测量范围，仅考虑检测范围内的路标，进而实现路标的动态管理。从图2、3中可以看出：PMCMC-RFS-SLAM算法相对EKF-FastSLAM算法对车辆位姿的估计性能平均提高了约1.5倍，且定位不存在跳变现象，相对比较平滑。其主要原因是PMCMC-RFS-SLAM算法不依赖特征相关结果，对特征的数量也不需要进行预定假设。

图2 东向定位误差

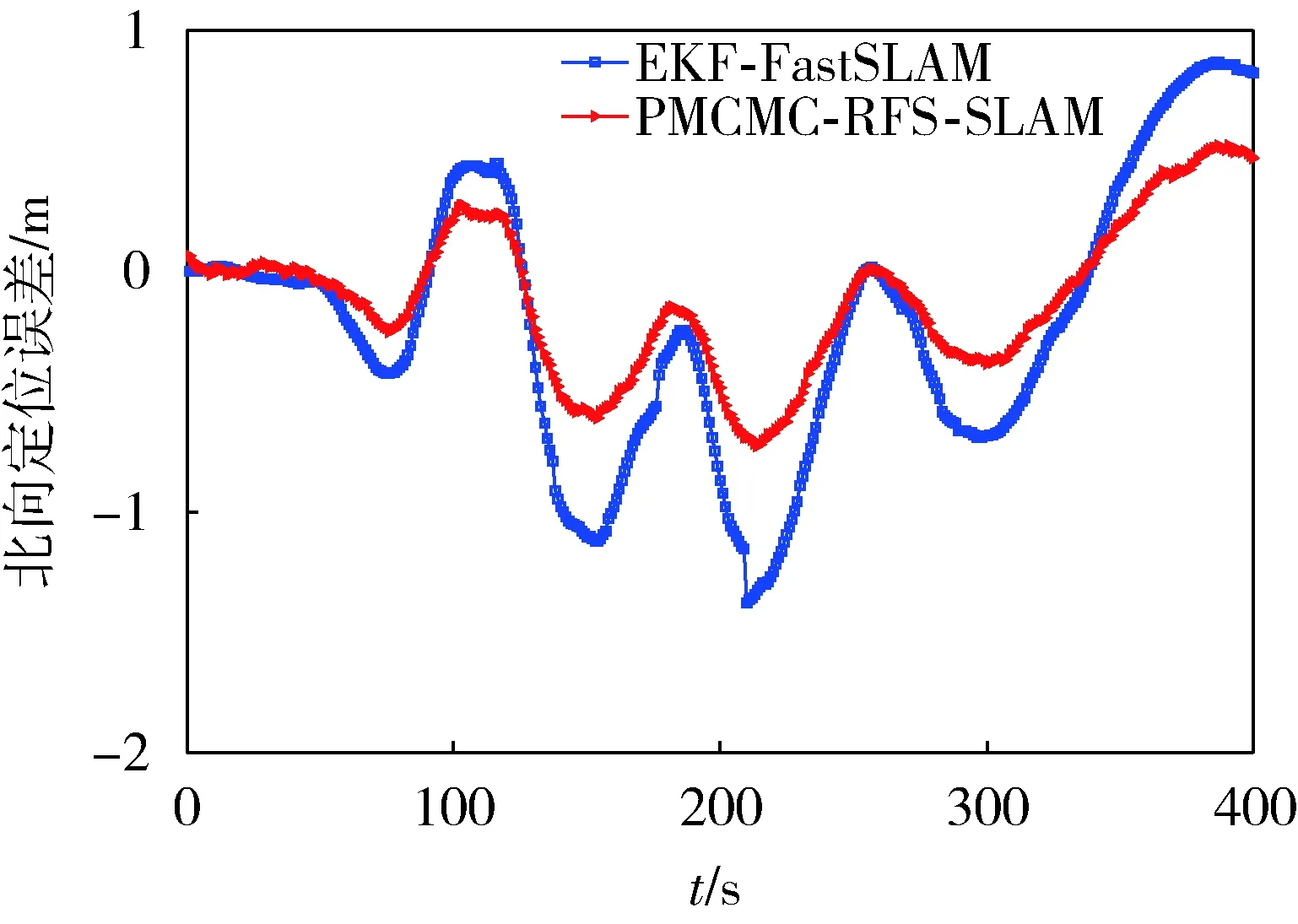
图3 北向定位误差

图4给出了当测量噪声增加时的滤波性能比较，可以看出：随着噪声水平的增加，PMCMC-RFS-SLAM算法性能基本保持稳定，而EKF-FastSLAM算法明显变差。

图4 当测量噪声增加时的滤波性能比较

通过分析图2-4给出的试验结果可知：与经典EKF-FastSLAM算法相比，在具有数据关联不确定和特征误检、漏检的情况下，RFS-SLAM算法能够准确地估计地图中的特征数量以及相应的位置。EKF-FastSLAM算法利用随机向量对自主车的状态转移和传感器的观测信息建模，只能描述观测信息的不确定性，而忽略了传感器漏检、噪声干扰误检以及特征数量不确定等问题;但这些问题又会对SLAM的过程估计产生很大的影响，尤其是影响数据关联的结果，从而导致定位和地图估计精度下降，甚至产生状态估计跳变。而对于RFS-SLAM算法，由于其采用RFS描述系统状态、环境地图和观测信息，在建模的过程中就已经包含了上述特征，能够更为真实地反映多特征、多观测的特点，同时避免了复杂的数据关联问题。

为了进一步验证算法的有效性，选择无人自主车平台为测试对象，采用64线三维激光雷达和惯性导航系统为感知器，以构建SLAM系统。鉴于RFS-SLAM算法通过PMCMC粒子滤波算法实现，因此选择经典的EKF-FastSLAM算法进行比较分析，EKF-FastSLAM算法选择最大似然数据关联。理论上，环境中所有特征都可以用来修正车辆的位姿估计，为了提高系统的可靠性和降低算法的计算复杂度，仍然选择树干和路灯杆作为路标特征。

PMCMC-RFS算法采用RFS构建的SLAM模型将多路标检测、跟踪及数据关联等问题集成到一个统一的贝叶斯框架内，根据计算的概率强度，图5、6分别给出了采用RFS计算得到的位置、路标估计和路标高斯混合后验强度。求解概率强度的局部极大值即可得到路标的位置，极大值的数量就是在传感器感知范围内的路标数量，如图6所示，可见：采用PMCMC-RFS算法解决了路标特征密集、动态特征多的复杂城乡环境中SLAM 求解鲁棒性差的问题，同时有效地解决了高维粒子滤波算法的提议分布选择和高维积分计算困难等问题。

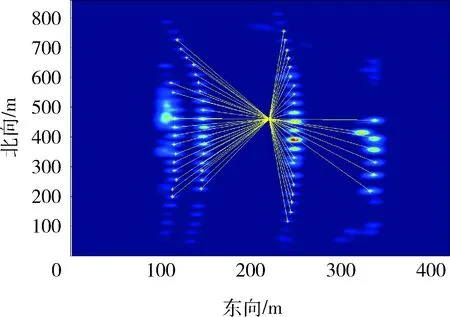
图5 采用RFS计算得到的位置和路标估计

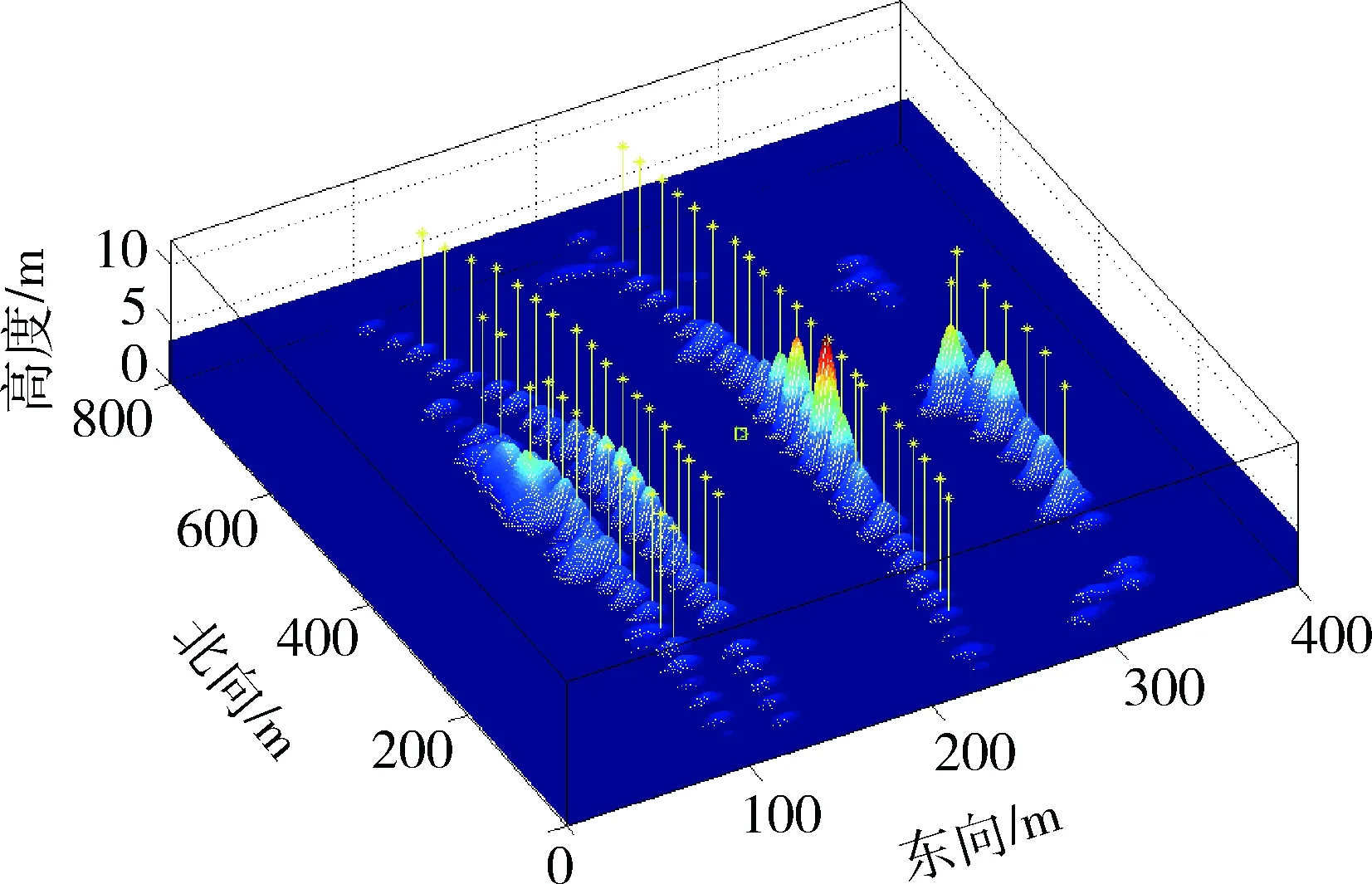
图6 采用RFS计算得到的路标高斯混合后验强度

4 结论

本文采用RFS理论构建了RFS-SLAM模型，并给出了求解集合上的高维积分的PMCMC计算方法。所构建的PMCMC-RFS-SLAM 算法与经典的EKF-FastSLAM算法相比，估计精度提高了大约50%，且解决了经典SLAM 算法对数据关联结果的严重依赖和地图动态管理问题，同时还能够估计视野范围内的特征数量，为准确的位姿估计提供了有效的途径，提高了复杂多路标特征环境SLAM算法的鲁棒性。

[1] Smith R C, Self M,Cheeseman P. A Stochastic Map for Uncertain Spatial Relationships[EB/OL].(2012-05-30)[2014-10-08].http://wenku.baidu.com/view/8ae34d87e53a580217fcfe00.html

[2] Dissanayake M G, Newman P, Clark S, et al. A Solution to the Simultaneous Localization and Map Building (SLAM) Problem[J]. IEEE Transactions on Robotics and Automation,2001,17(3):229-241.

[3] Martinez-Cantin R, de Freitas N, Castellanos J A. Analysis of Particle Methods for Simultaneous Robot Localization and Mapping and a New Algorithm: Marginal-SLAM[C]∥Proceedings of 2007 IEEE International Conference on Robotics and Automation.Roma,Italy:IEEE, 2007: 2415-2420.

[4] Martinez-Cantin R, Castellanos J A. Unscented SLAM for Large-scale Outdoor Environments[C]∥Proceedings of 2005 IEEE International Conference on Intelligent Robots and Systems.Roma,Italy:IEEE,2005:3427-3432.

[5] Havangi R, Nekoui M A, Teshnehlab M, et al. A SLAM Based on Auxiliary Marginalised Particle Filter and Differential Evolution[J]. International Journal of Systems Science, 2014, 45(9): 1913-1926.

[6] Nemeth C, Fearnhead P, Mihaylova L. Sequential Monte Carlo Methods for State and Parameter Estimation in Abruptly Changing Environments[J]. IEEE Transactions on Signal Processing, 2014, 62(5): 1245-1255.

[7] Yoon J H, Kim D Y, Yoon K J. Efficient Importance Sampling Function Design for Sequential Monte Carlo PHD Filter[J]. Signal Processing, 2012, 92(9): 2315-2321.

[8] Mullane J, Vo B N, Adams M D, et al. A Random-Finite-Set Approach to Bayesian SLAM[J]. IEEE Transactions on Robotics,2011, 27(2): 268-282.

[9] Du H Y,Zhao Y X,Yang Y P, et al. SLAM Algorithm Based on Random Finite Set[J]. Systems Engineering and Electronics, 2012, 7:29037.

[10] Vo B N, Singh S, Doucet A. Sequential Monte Carlo Methods for Multitarget Filtering with Random Finite Sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4):1224-1245.

(责任编辑:尚彩娟)

Autonomous Vehicle SLAM Algorithm Based on PMCMC-RFS

SU Kui-feng, CHANG Tian-qing, ZHANG Lei, YANG Guo-zhen

(Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

Aiming at the problem of Simultaneous Localization And mapping (SLAM) for autonomous vehicles, the environment feature as well as vehicle position and attitude are described by using Random Finite Set (RFS), which integrates the aspects such as multi-feature detection, tracking, recognition and correlation related to SLAM algorithm into a single unified Bayesian framework so that the thorny problem that the algorithm of posterior estimation and information fusion relies on the result of association greatly can be effectively solved. Meanwhile, to calculate the complex joint posterior estimation distribution and resolve the proposal distribution selection difficulties in particle filtering algorithm, SLAM resolving method based on Particle Markov Chain Monte Carlo (PMCMC) is proposed using Sequential Monte Carlo (SMC) and Markov Chain Monte Carlo (MCMC). The autonomous ground vehicle experimental results shows that the proposed method can estimate in dynamic manner the feature numbers of perspective scope and has better performance in states estimation without consideration of data association.

Simultaneous Localization And Mapping (SLAM); Random Finite Set (RFS); Markov Chain Monte Carlo (MCMC); particle filter

1672-1497(2015)02-0070-06

2014-12-08

军队科研计划项目

苏奎峰(1976-)，男，讲师，博士。

TP24

A

10.3969/j.issn.1672-1497.2015.02.014