靶场加注系统中阀门特性对管内瞬变过程的影响

高 阳， 冯辅周， 张红星

(1. 装甲兵工程学院机械工程系， 北京 100072； 2. 太原卫星发射基地， 山西 太原 036304)

靶场加注系统中阀门特性对管内瞬变过程的影响

高 阳1， 冯辅周1， 张红星2

(1. 装甲兵工程学院机械工程系， 北京 100072； 2. 太原卫星发射基地， 山西 太原 036304)

针对推进剂加注系统工序转换中因瞬变过程而导致的安全隐患问题，采用数值计算方法，从阀门的特性及动作规律角度入手，研究其对加注工序转换过程中管道压力及流量瞬变过程的影响。通过理论分析与基于案例的数值计算发现：阀门的固有特性与动作规律共同影响着瞬变过程，相同的瞬变结果可由不同类型的阀门与相应的阀门动作规律实现；在阀门动作时间一定，且大于压力波传播周期的情况下，动作规律指数m与固有特性指数n之积等于1时所产生的压力峰值最小；随着mn值偏离数值1程度的增大，管道压力峰值逐渐增大，管道中出现汽蚀的风险也加大。因此，在推进剂加注过程中，应针对阀门类型选择阀门动作规律，以有效控制管内瞬变过程。

加注系统；阀门；瞬变过程；汽蚀

推进剂加注系统的主要任务为在火箭(导弹)发射前指定时间内将液体燃料准确、安全、快速地输送至火箭(导弹)贮箱中，该过程是影响发射成败的关键环节之一[1]。推进剂加注系统通常由加注泵、管道、各类开关阀及电调阀、仪表和控制系统等组成。在加注过程中，为了满足不同工序的加注要求，推进剂的流量及流动路径需要进行多次调整，调整过程主要是通过改变加注泵的转速及相关阀门的开度(或开闭)来实现。若调整过程设置不当，将导致管内压力和流量的瞬时突变，从而产生强烈的流体瞬变过程，该现象也称水锤现象，其压力峰值可达稳定运行时的数倍甚至更高[2-3]，从而严重影响加注过程的安全进行。

国内外均出现过因水锤现象而导致加注系统破坏的报道[4-7]，然而国内在加注系统的水力设计中却较少考虑预防水锤的问题。国外学者[8-11]在确定阀门类型的情况下，根据多种数值寻优计算结果指出：通过调节阀门的动作规律可以有效地控制水锤压力峰值。但以上研究未能给出阀门动作规律与阀门自身特性间的关系。万五一等[12]虽然注意到了上述关系的存在，但同样未能揭示这种关系的实质。由于加注系统中存在多种类型的阀门，其特性各异，因而在不同加注阶段，为控制系统的瞬变过程，应采用的阀门动作规律也存在一定程度的区别。本文主要通过研究关阀过程中阀门特性与阀门关闭规律对管内压力及流量等参数瞬变过程的影响，寻找与阀门特性匹配的阀门动作规律，以削弱瞬变过程的强度，从而降低加注工序转换过程的风险。

1 瞬变流模型

一维管道瞬变流模型由连续性方程和运动方程组成[13]：

(1)

式中：P为表压强；V为截面平均速度；D为管道内径；θ为管道相对水平面的倾角；τ0为壁面施加给流体的剪切应力，通常取准恒定模型；ρ为流体密度；g为重力加速度；

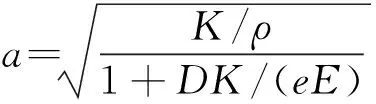
(2)

为管道波速,其中，K为流体的体积弹性模量，e为管道厚度，E为管道杨氏弹性模量。

由于a>>V，因而可忽略模型中对流项，又设管道水平，可进一步简化模型。用水头H、流量Q分别代替模型中的P、V，根据特征线理论[14]，可将模型中的偏微分方程化为特征线上的常微分方程：

(3)

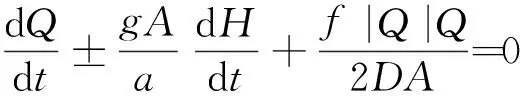
(4)

式(4)中第2项的符号取决于式(3)右侧符号，且式(4)仅在满足式(3)的曲线簇上成立。从式(4)可以看出：管道压力变化的剧烈程度主要取决于流量变化的快慢。

2 阀门特性

通常可将阀门视为节流元件，在定常状态下有

Q=(CdAv)(2gΔh)1/2=Kv(ΔP)1/2，

(5)

式中：Cd为阀门排量系数；Av为阀口流通面积；Δh为阀门进出口水头差，将其转换为标准单位后即为进出口压差ΔP；Kv为阀门流量系数。

令阀门的进出口压差恒定，分别用下标“1”、“2”表示阀门的2种不同开度状态，则有

(6)

式中:τ21的取值因阀门在2种状态下的开度而异。当令状态“1”为阀门全开状态时，τ21将只与状态“2”的阀门开度有关，此时将τ21简化表示为τ。令阀门由全闭到全开的行程为α0，由全闭到任意开度的行程为α，则有

τ=f(α/α0),

(7)

式(7)即为阀门的理想流量特性，通常通过试验得到，它是阀门的固有特性。阀门理想流量特性可由简单幂函数[15]表示为

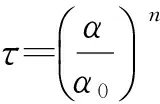
(8)

式中：n∈R+，它的不同取值对应不同类型的阀门，如图1所示。

图1 阀门特性曲线

令r=α/α0为阀门相对开度，由式(6)、(8)可得

Q=Qmaxrn，

(9)

对式(9)关于r取导数可得

(10)

显然，对于n∈(1,+∞)，随着开度的增加，单位开度变化引起的流量变化将越来越大；而对于n∈(0,1),则恰好相反。

3 阀门特性与瞬变过程关系

为不失一般性，取介质为清水，参照文献[16]，考虑简单管模型，即在长L=600 m、直径D=0.5 m的水平管上游设置液位恒定为Hr=150 m的水源，下游设置阀门与大气连接，如图2所示。

图2 简单管模型

模型中管道波速a=1 200 m/s，管道摩擦因数为f=0.018，(CdAv)0=0.009 m2。最初阀门处于全开状态，管内流量为Q0，阀门将在时间t0内由稳定的全开状态按照如下规律完全关闭：

r=α/α0=(1-t/t0)m。

(11)

式中:m为阀门的动作规律指数。取t0>2L/a，即不考虑直接水锤情况，该假设符合加注系统结构特点，因为在加注系统中阀门通常安装在较短的直管道上，而阀门动作时间通常在1 s左右。

由式(8)、(11)可得

τ=(1-t/t0)mn。

(12)

忽略水源侧管道入口处水头损失，令式(12)中的m=1，即阀门线性关闭，参照文献[16],取t0=2.1 s，分别令n=0.2，0.5，1.0，1.5，3.0，暂不考虑汽蚀的影响，采用特征线方法(Method Of Characteristics,MOC)计算阀门前节点的流量及压力随时间的变化情况，分别如图3、4所示。

通过对比可知：图4中红色曲线(m=1，n=1.5)与文献[16]中结果一致，从而验证了算法的正确性。由图3可见：当m=1时，在关阀过程中，随着n值的增大，阀门前流量发生剧烈变化的时段从关阀后期向前期转移。综合分析图3、4可知：在阀门前流量发生剧烈变化的同时，也伴随着压力的急剧变化，压力峰值出现的时刻也向前转移。

图3 不同阀门特性下的阀前流量随时间变化曲线

图4 不同阀门特性下的阀前压力随时间变化曲线

从图4中各曲线压力峰值来看：在m=n=1时产生的压力峰值最小，且压力过渡相对平缓。从图3也可以发现：在m=n=1时阀前流量变化速率近似线性，比较稳定。此外，从图4还可以看出：随着n值远离1，阀前出现负压的风险加大，极易形成汽蚀，存在进一步产生更为剧烈的弥合水锤的可能。

令式(12)中n=1，即阀门流量特性为线性，取t0=2.1 s，分别令m=0.2，0.5，1.0，1.5，3.0，同样暂不考虑汽蚀的影响，计算得到的阀门前节点的流量及压力波动情况分别与图3、4一致，仅需将图中m和n的值调换即可。事实上，从式(12)可以看出：m和n共同决定着τ与t之间的关系，虽然m与n的物理意义不同，但在MOC的计算过程中m和n本身是可互换的，只要它们的乘积相同，就会得到相同的计算结果。分别取mn=0.1，0.5，0.8，1.0，1.2，1.5，5.0，在此基础上分别取不同m、n的组合进行数值计算，计算所得瞬变压力峰值如表1所示。

表1 不同m、n组合下计算所得瞬变压力峰值

从表1中可以看出：当mn=1时所获得的压力峰值最小，随着mn取值远离1，压力峰值逐步增大，且向mn<1方向增加迅速。

由上述分析可知：在边界条件及初始值一定，且阀门动作时间大于压力波传播周期2L/a的情况下，可得到如下结论。

1) 阀门动作在管道中产生的瞬变效果主要由2方面因素共同决定，即阀门固有特性和阀门动作规律：前者取决于n值;而后者取决于m值。

2) 管道中的相同瞬变效果可由不同类型的阀门与其相应的动作规律来实现。

3) 在相同的关闭时间内，当mn=1时，所产生的压力峰值最小，且压力过渡平缓。

4)mn取值偏离1的程度越大，阀前出现负压的可能性越大，越容易形成汽蚀。当mn>>1时，关阀初期阀门处将出现剧烈的流量变化，从而引起较大的压力波动；当mn<<1时，这种剧烈的流量变化将出现在关阀末期，同样会引起很大的压力波动。

5) 随着阀门关闭时间t0的延长，单位时间内阀门的行程变化将减小，因而所引起的流量变化随之减小，根据式(4)及上述案例的分析，在整个关阀过程中所引起的压力变化也将减小。

由于在推进剂加注管路中球阀应用最多，因而在此需要对它进行特别的说明。按照本文分析，为了降低球阀关闭过程中的瞬变过程强度，应使mn=1，即m=1/3，在上述案例中，球阀的关闭规律应如图5所示。通过对比图5及图1中的球阀特性曲线可知两者的变化刚好相反：图5中随着开度的减小，单位时间内阀门的行程越来越大；而图1中随着开度的减小，单位开度阀门的流量变化越来越小。

图5 球阀关闭规律

4 结论

为削弱加注系统工序调整过程中产生的瞬变过程强度，以避免其对系统的破坏，本文从在调整过程中起重要作用的阀门入手，通过理论分析及仿真计算，研究了阀门的特性及其关闭规律与管内瞬变过程的关系，并得到了阀门类型与其关闭规律的最佳匹配关系。理论上该匹配关系对包括加注系统在内的各种管道系统均适用。

由于推进剂加注系统结构复杂，管道众多，管内瞬变过程的影响因素多样，阀门仅是其中最重要的因素之一，因而下一步将对其他因素进行分析，并在此基础上寻求对管内瞬变过程的最优控制方法。

[1] 周载学. 发射技术:下[M]. 北京: 中国宇航出版社, 2009.

[2] 王鑫,韩伟实. 压水堆核电厂主给水管道水锤计算及分析[J]. 原子能科学技术, 2010, 44(S1): 192-197.

[3] 田淳, 张宗坤, 郝瑞霞,等. 电厂输水管道水击波传播过程仿真[J]. 计算机仿真, 2011, 28(11): 279-282.

[4] 何家声. 低温系统水击及其防范[J]. 航天发射技术, 2007(90): 34-37.

[5] Moor W I,Arnold R I. Failure of Appollo Saturn V Liquid Oxygen Loading Systems[J]. Advances in Cryogenic Engineering, 1968(13): 13-16.

[6] 尼亚波部拉诺夫瓦费林. 液体低温系统[M]. 赵运生，崔春娥，译.北京: 低温工程编辑部, 1993.

[7] 高阳, 冯辅周, 江鹏程,等. 火箭靶场加注系统瞬变过程及其影响因素试验研究[J]. 机械设计与制造, 2015(3): 82-86.

[8] Streeter V L. Valve Stroking to Control Waterhammer[M]. Michigan: The University of Michigan Industry Program of the College of Engineering, 1962.

[9] Propson T P. Valve Stroking to Control Transient Flows in Liquid Piping Systems[M]. Michigan: The University of Michigan Industry Program of the College of Engineering, 1970.

[10] Driels S M. Valve Stroking in Separated Pipe Flow[J]. Journal of Hydraulic Division, 1974, 100(11): 1549-1563.

[11] Yao E, Kember G,Hansen D. Analysis of Water Hammer Attenuation in Applications with Varying Valve Closure Times[J]. Journal of Engineering Mechanics, 2015, 14(1): 1-9.

[12] 万五一, 练继建,李玉柱. 阀门系统的过流特性及其对瞬变过程的影响[J]. 清华大学学报:自然科学版, 2005, 45(9): 1198-1201.

[13] Chaudhry M H. Applied Hydraulic Transients[M]. New York: Springer, 2014.

[14] 王学芳, 叶宏开, 汤荣铭,等. 工业管道中的水锤[M]. 北京: 科学出版社, 1995.

[15] Azoury P H, Baasiri M,Najm H. Effect of Valve-closure Schedule on Water Hammer[J]. Journal of Hydraulic Engineering, 1986,112(10): 890-903.

[16] Wylie E B,Streeter V L. Fluid Transients[M]. New York: McGRAW-HILL International Book Company, 1978.

(责任编辑:尚彩娟)

Influence of Characteristics of Valve in Loading System of Launch Site on Hydraulic Transients in Loading Pipes

GAO Yang1, FENG Fu-zhou1, ZHANG Hong-xing2

(1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China;2. Taiyuan Launching Base of Satellites, Taiyuan 036304, China)

Considering the potential hazards during the loading period transformation in propellant loading system, from the perspective of valve characteristics and its action trail, this paper studies their influence on pipe transient pressure and flow rate using numerical method. With the help of theoretical analysis and numerical computation, some meaningful points become clear: both valves’ inherent characteristics and action trail influence transient process in pipes, and the similar transient process could result from different combination of valve type and valve action trail; with constant valve action time which is longer than the propagation period of pressure wave, the pressure peak reaches its minimum when the product value ofmnis 1, wheremis the valve action trail exponential andnis the inherent characteristics one; with the deflection ofmnfrom 1, both the pressure peak and the possibility of cavitation increase. Therefore, during the loading process, in order to control the transient process efficiently, the action trail of valve should be determined according to the valve’s type.

loading system; valve; transient process; cavitation

1672-1497(2015)02-0081-04

2014-11-30

军队科研计划项目

高 阳(1986-)，男，博士研究生。

V554+.4

A

10.3969/j.issn.1672-1497.2015.02.016