基于电磁驱动的引信动态模拟研究

詹 超， 向红军， 雷 彬

(军械工程学院弹药工程系， 河北 石家庄 050003)

基于电磁驱动的引信动态模拟研究

詹 超， 向红军， 雷 彬

(军械工程学院弹药工程系， 河北 石家庄 050003)

针对引信模拟试验传统方法的不足，提出了将电磁发射技术应用到引信模拟试验中。阐述了基于电磁驱动的引信模拟系统的结构组成和工作原理，建立了数学模型，并通过对所建模型的仿真分析，验证了电磁发射技术在引信模拟试验中应用的可行性，分析了充电电压、电容和触发位置对试验弹受力和速度的影响，结果表明：通过调节这些参数，可根据所模拟引信的要求改变试验弹受力情况。

电磁驱动；引信；动态模拟

引信作为弹药的控制部分，对弹药的安全性和可靠性起着至关重要的作用。目前，对引信的性能检验主要有靶场试验和实验室模拟试验[1]。传统的实验室模拟试验装置包括基于气体炮和真空炮的试验[2-3]装置以及基于小型火箭[4]的试验装置，但是这些试验装置都存在设备笨重、操作复杂、模拟结果不精确和模拟引信型号单一等缺点。电磁发射技术作为一种新的驱动技术，将其应用到引信的模拟发射中，具有控制精确、适应性好、结构相对轻便以及可实现设备全电化等优点。电磁发射技术兴起于20世纪初，自20世纪60年代以来得到迅速发展[5-7]。目前，世界各国都将电磁发射技术作为未来武器系统的驱动方式，美国在电磁发射技术领域一直处于世界领先地位[8]。电磁发射主要分为电磁轨道发射和电磁线圈发射，其中，线圈发射又分为同步感应、异步感应和螺旋线圈3类发射方式。由于同步感应线圈发射方式具有弹丸无需连接外部电源、力学结构合理、发射管为圆柱管状等特点，相比较而言最适合作为引信动态模拟的驱动方式。同步感应线圈炮模拟引信环境力作为一种新的方法，其研究主要集中在原理分析、仿真试验和样机研制阶段。由电磁线圈驱动的试验弹速度主要由脉冲功率电源的储能决定，由于受试验条件限制，现阶段主要以低初速弹药的引信为研究对象，如迫击炮和枪榴弹引信。本文仿真模型基于枪榴弹引信模拟要求进行设计。

1 结构组成与工作原理

1.1 结构组成

引信动态模拟系统由直线驱动系统、旋转电机、试验弹和接收装置等组成，其中：直线驱动系统主要由高功率脉冲电源(脉冲储能电容器)、三电极间隙放电开关、驱动线圈、电枢及触发控制电路等组成，如图1所示；试验弹由引信加固装置、电磁屏蔽装置及内置的引信体组成。电枢受电磁力作用向前推动试验弹运动，完成引信膛内受力的模拟。

图1 直线驱动系统基本组成

1.2 工作原理

驱动线圈由高功率脉冲电源馈电，当闭合开关时，驱动线圈在脉冲电流的作用下产生变化的磁场，使电枢产生感应电流(涡流)，通过其与磁场相互作用产生电磁力，推动试验弹运动。对于膛内加速时间长或者膛压曲线复杂的引信，可以设计多级加速。即当被第1级加速的试验弹运动到第2级驱动线圈的合适位置后，给第2级驱动线圈馈电，电枢中感应出的涡流与驱动线圈产生的磁场相互作用，产生电磁力，推动发射组件继续被加速。以此类推，试验弹被一系列驱动线圈不断加速，直到达到受力模拟要求。本文采用单级线圈驱动，对电磁发射技术在引信中的应用做初步的分析和论证。

2 数学模型

数学模型主要包括等效电路方程、动力学方程和运动学方程。

2.1 等效电路方程

驱动系统的等效电路如图2所示，其中：R0、L0分别为供电回路电阻和电感；R1、L1分别为驱动线圈的电阻和电感；R2、L2分别为电枢的电阻和电感；C为电容器电容。为了消除回路中的反向电流，在回路中加入了续流硅堆D。

图2 驱动系统的等效电路

在t时刻，等效电路方程如下：

(1)

(2)

式中：U0为电容器初始充电电压；M12为驱动线圈与电枢的互感；i1为驱动线圈回路电流；i2为电枢回路电流。

2.2 动力学方程

对于弹丸受到的电磁力，可以采用电感法进行计算，其依据[7]是：力是储存能量在运动中的变化率，即在运动方向上的能量梯度。在理想情况下，图2所示的单级感应线圈炮在t时刻系统总储能为

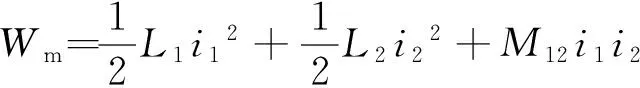
(3)

发射组件沿水平方向运动，自感项磁能不变化，只有互感项磁能随位置变化。在不考虑摩擦力和空气阻力影响的情况下，t时刻作用在发射组件上沿水平方向的力为

(4)

2.3 运动学方程

设装有引信的试验弹质量为mp，由引信驱动系统的动力学方程可得试验弹t时刻的加速度为

(5)

t时刻试验弹的速度为

(6)

t时刻试验弹的位移为

(7)

3 驱动系统工作过程动态仿真

3.1 仿真模型

由于受电感梯度随位置变化、驱动线圈电流瞬间发电以及试验弹位置变化等因素的影响，试验弹所受驱动力的理论计算十分困难。本文采用有限元分析软件对所建立的模型进行仿真，仿真模型如图3所示。

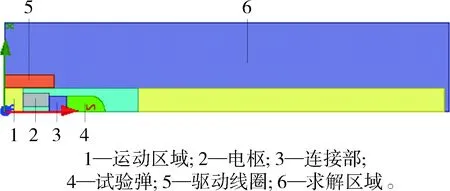
图3 仿真模型

采用电磁场有限元分析软件对引信模拟发射模型进行静磁场仿真分析[9-10]。由于驱动系统为轴对称结构，采用柱坐标系(Z-R)仿真环境，可以简化为二维模型，这样既可以保证计算精度，又可以大大降低计算量。

图3给出的驱动线圈发射器的仿真模型中，包括运动区域、求解区域、电枢及驱动线圈。运动区域和求解区域的材料属性分别设为空气、真空。图4给出了仿真区域的网格划分情况，为了保证仿真计算精度，将弹丸、驱动线圈及运动区域的网格划分得比较密集，而将求解区域的网格划分得相对比较稀疏。

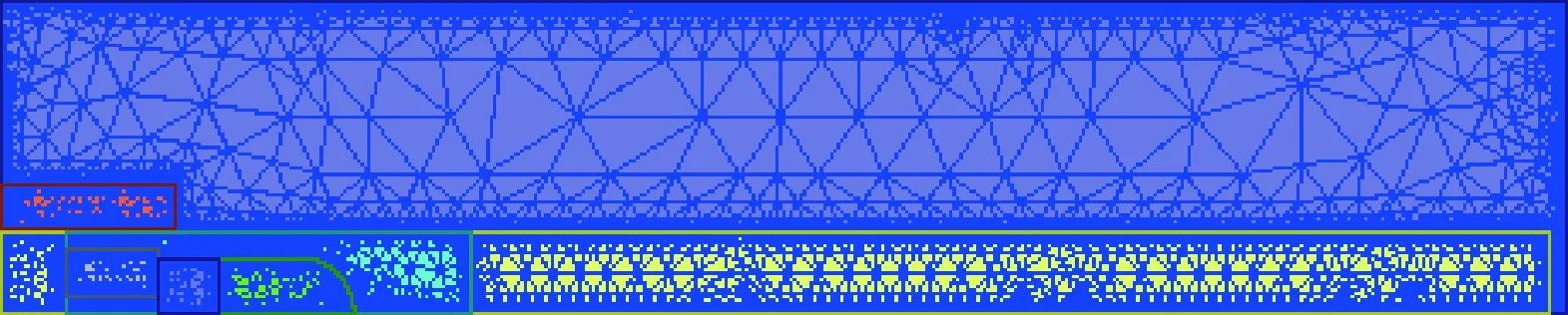
图4 仿真区域的网格划分

在仿真过程中，通过外接电路的方式为驱动线圈加载电压，仿真外接电路如图5所示。在外接电路中，脉冲储能电容器的电压设置为8 kV，电容设

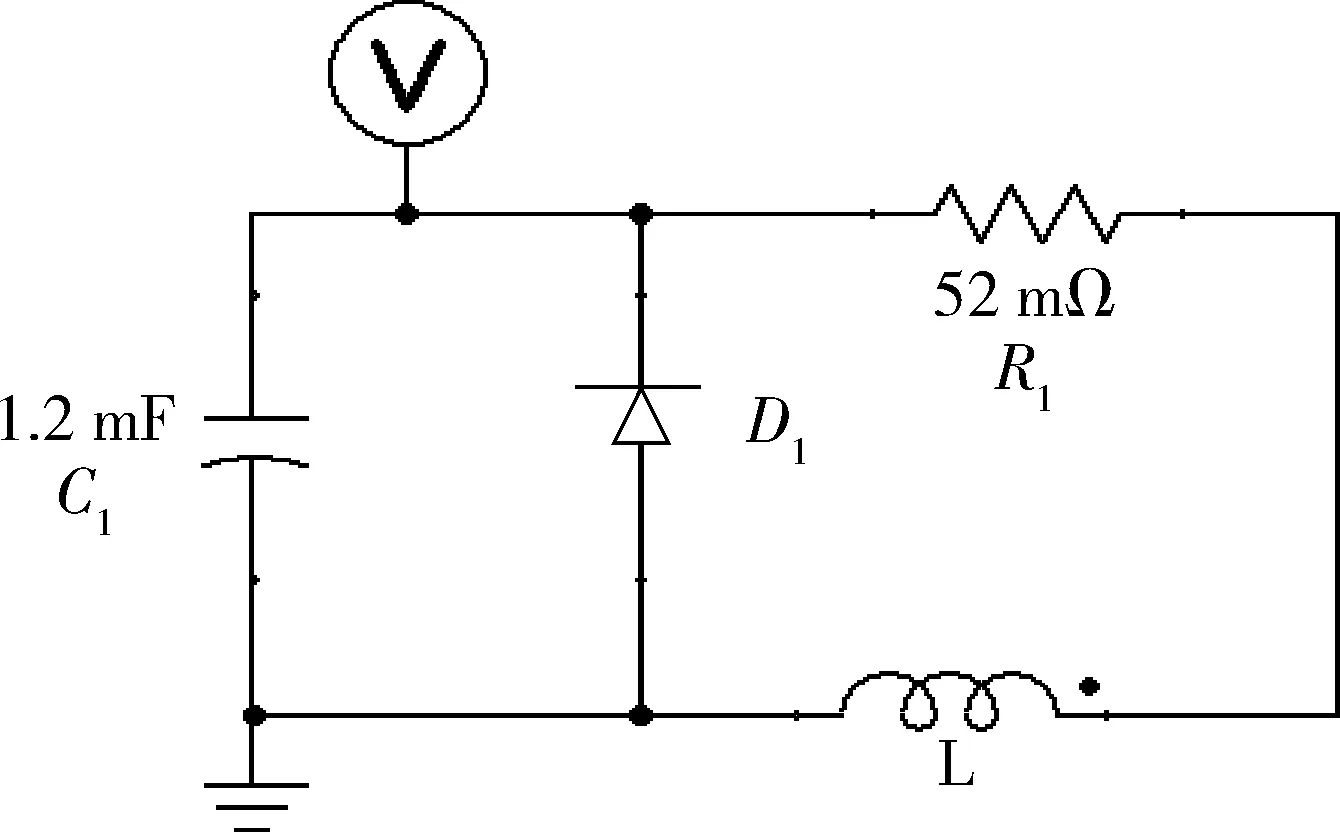
图5 仿真外接电路

置为1.2 mF，驱动线圈的电阻为52 mΩ，仿真的起始时间为0 ms，终止时间为3 ms，仿真时间步长为0.01 ms。

3.2 仿真结果分析

仿真结果中，电压、电流、电磁力和速度随时间的变化曲线分别如图6-9所示。从图6可以看出：电容器的初始充电电压为8 kV，放电开始后，电压逐渐下降，在1.2 ms时电容器两端的电压衰减到0 V。从图7可以看出：驱动线圈的放电电流先逐渐增大，在1 ms时驱动线圈的最大放电电流为11 kA，此后驱动线圈的电流逐渐衰减，直到0 A。从图8可以看出：发射过程中，试验弹受到的电磁力先增大后减小，在1.05 ms时驱动线圈电磁力最大，为68.9 kN，在试验弹总质量为0.6 kg时，其最大加速度(即引信受到的最大过载)约为11.483×103g(g为重力加速度)。从时间上也可以看出：在驱动线圈的放电电流达到最大值时，电磁力并没有同步达到最大值，而是有0.05 ms的延迟。从图9可以看出：试验弹经过加速，电枢速度逐渐增大，在t=1.85 ms时得到的最大发射速度为107.8 m/s，此后近似做匀速运动。

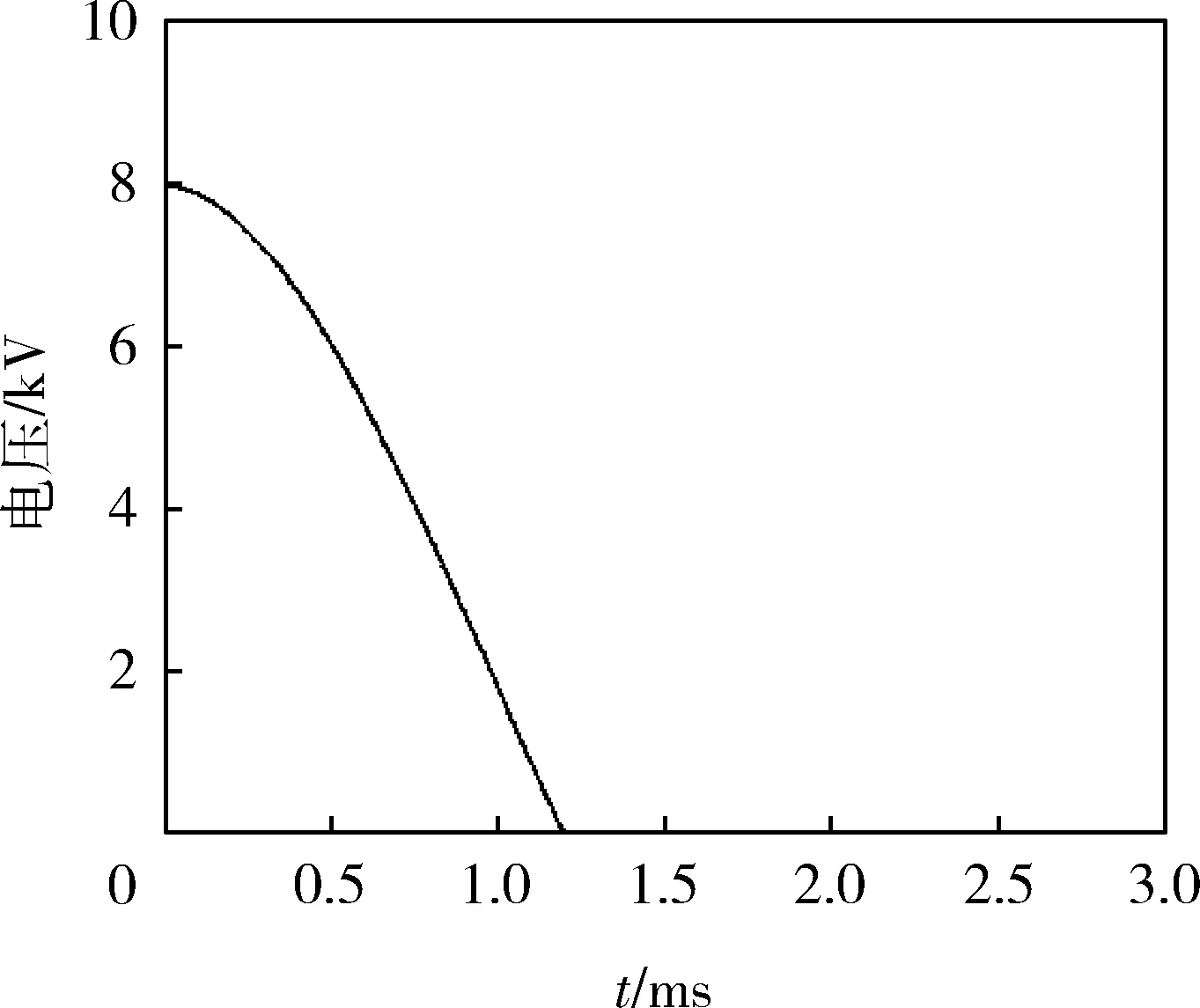
图6 电压随时间的变化曲线

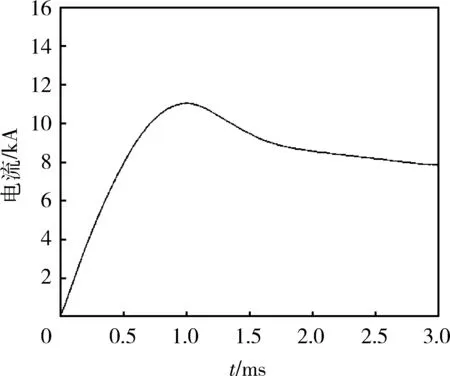
图7 电流随时间的变化曲线

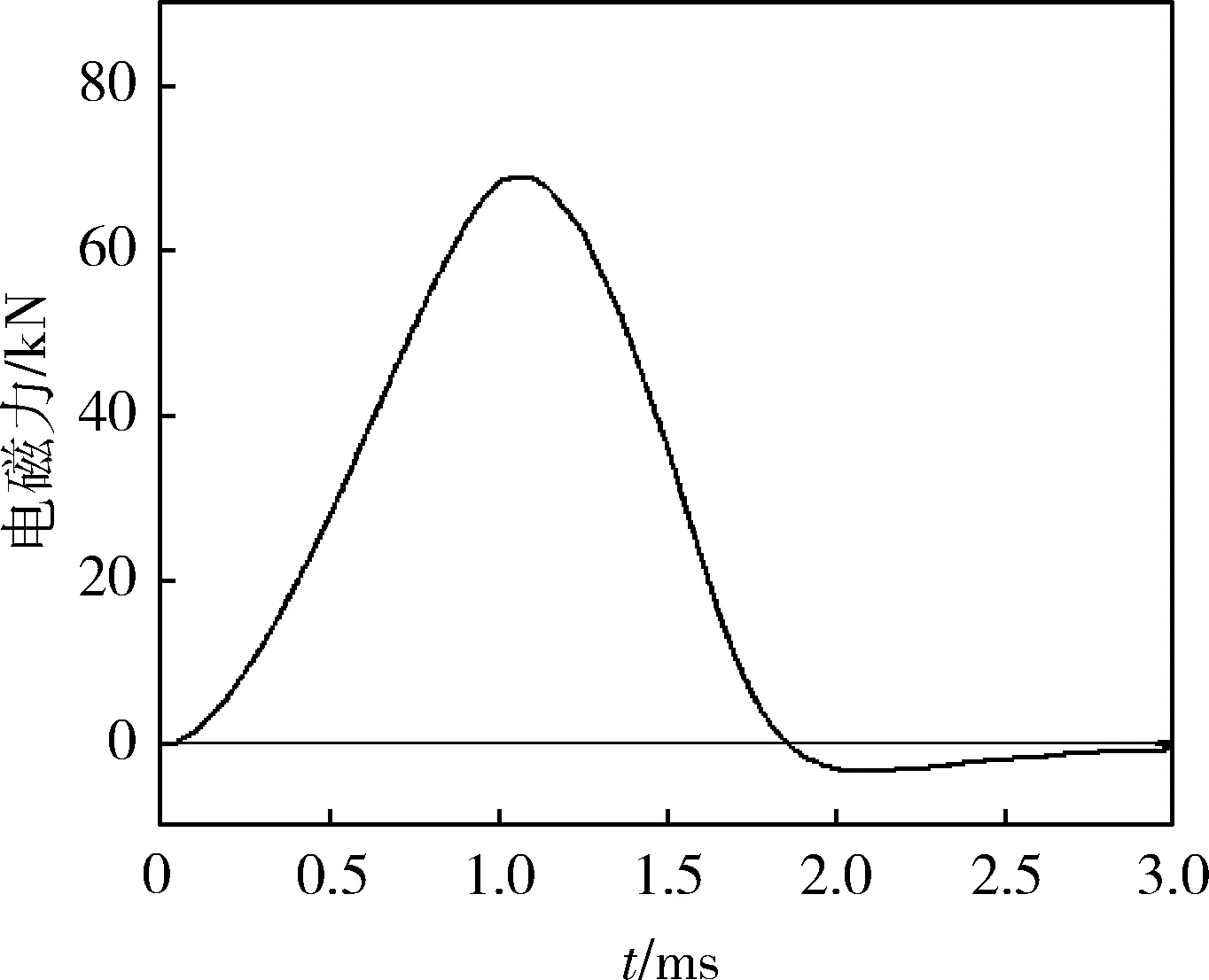
图8 电磁力随时间的变化曲线

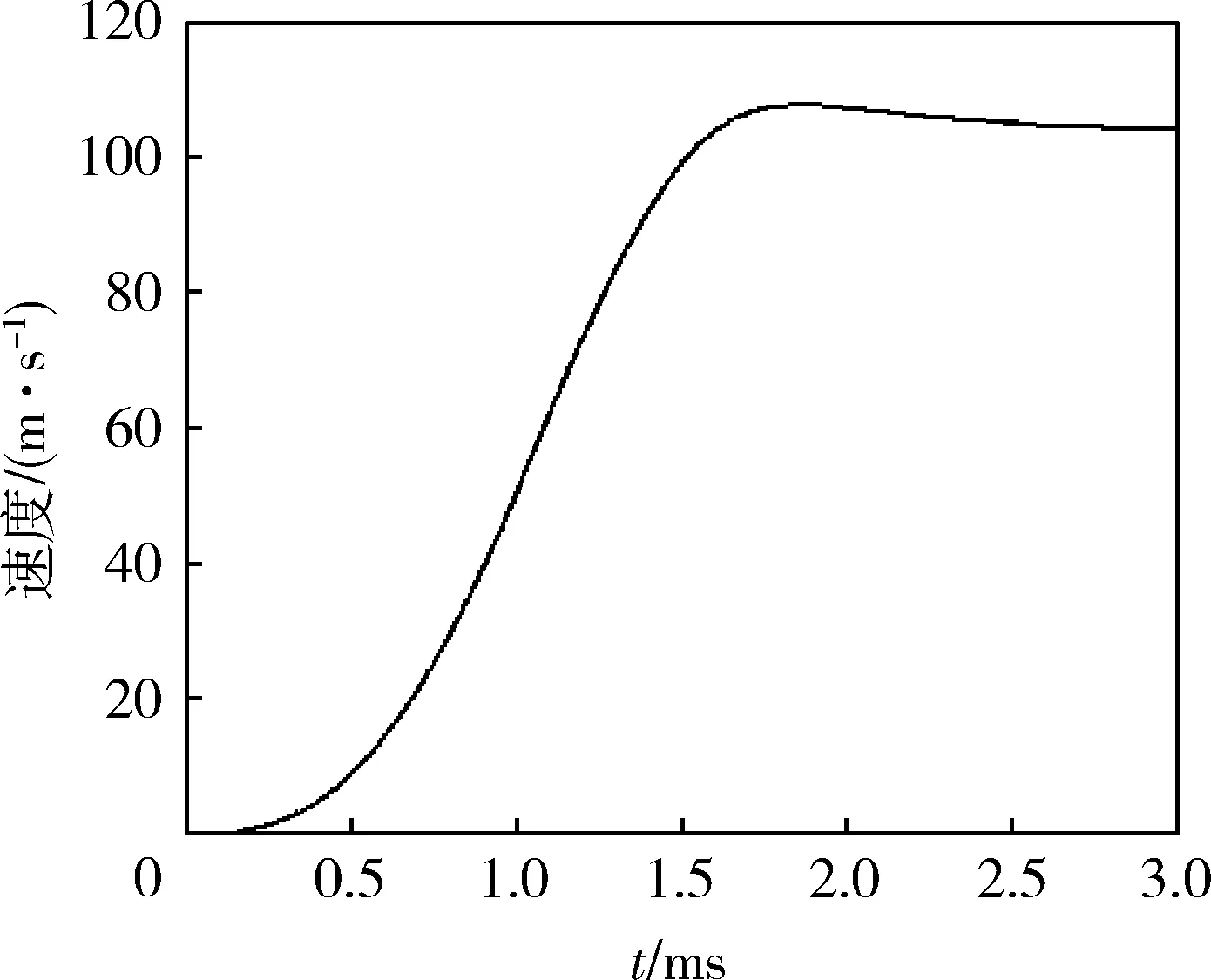
图9 速度随时间的变化曲线

以上仿真结果表明：通过电磁直线加速器可以实现对试验弹的加速，用以模拟引信发射过程中受到的最大直线加速惯性力。

4 充电电压、电容和触发位置对弹道特性的影响

4.1 充电电压、电容对弹道特性的影响

1) 充电电压对弹道特性的影响

在仿真模型和电路其他参数不变的情况下，分别设定充电电压为5、6、7、8、9、10 kV。经过仿真计算，得到不同充电电压下试验弹所受电磁力和速度随时间的变化曲线，分别如图10、11所示。

图10 不同充电电压下试验弹所受电磁力 随时间的变化曲线

图11 不同充电电压下试验弹速度 随时间的变化曲线

从图10可以看出：充电电压为5、6、7、8、9、10 kV时，试验弹受到的最大电磁力分别为23.4、35.9、51.5、68.9、89.5、110 kN，即随着充电电压的增大，试验弹受到的最大电磁力也在逐渐增大，并且所受电磁力的上升和下降速度也明显增大。受力上升阶段越陡，即所模拟的加速度越大，加速过程更加明显，这表明：通过调整储能电容器的充电电压，可以实现对引信受到的直线加速惯性力的调整，从而实现不同引信受到的直线加速惯性力的动态模拟，满足一种试验平台可同时模拟多种引信的需要。

从图11可以看出：不同充电电压下试验弹的速度都是先上升，然后逐渐趋于平稳；充电电压为5、6、7、8、9、10 kV时，对应的试验弹最大初速分别为57.4、73.9、90.8、107.8、125.1、141.5 m/s，即随着充电电压的增大，试验弹的最大初速也在逐渐增大。

2) 充电电容对弹道特性的影响

在相同仿真模型以及充电电压为8 kV且保持不变的情况下，改变充电电路电容为0.9、1.2、1.5、1.8 mF，仿真分析得到的试验弹所受电磁力和速度随时间的变化曲线分别如图12、13所示。

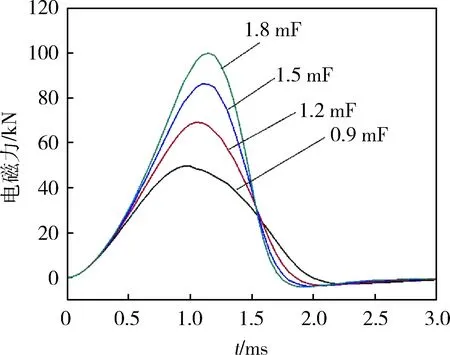
图12 不同充电电容下试验弹所受电磁力 随时间的变化曲线

图13 不同充电电容下试验弹速度 随时间的变化曲线

从图12可以看出：充电电容为0.9 mF时，在t=0.95 ms时刻，试验弹受到的最大电磁力为49.5 kN；充电电容为1.2 mF时，在t=1.05 ms时刻，试验弹受到的最大电磁力为68.9 kN；充电电容为1.5 mF时，在t=1.1 ms时刻，试验弹受到的最大电磁力为86.2 kN；充电电容为1.8 mF时,在t=1.15 ms时刻，试验弹受到的最大电磁力为100 kN。可见：随着充电电容的增大，试验弹受到的峰值过载逐渐增大，而且电磁力的上升和下降速度也在逐渐增大。

从图13可以看出：随着充电电容的增大，试验弹速度也在逐渐增大，充电电容为0.9、1.2、1.5、1.8 mF时，对应的试验弹峰值速度依次为89、107.8、123.5、136.2 m/s。

综合分析电容器的充电电压和充电电容可以看出：增大充电电容和充电电压，都可以使试验弹受到的峰值过载和试验弹的速度增大。但增大充电电容会使试验弹受到的电磁力前沿更加陡峭，呈现尖峰状态，这与引信实际的内弹道特性存在一定的差异。因此，要使电磁力的上升沿或下降沿比较平缓，以模拟峰值过载的持续时间，可以通过综合调整充电电压、充电电容予以实现。

从分析结果也可以看出：通过调整充电电压和充电电容，可以比较方便地调整试验弹的内弹道特性，以模拟不同引信的直线加速惯性力。

4.2 触发位置对弹道特性的影响

为分析不同初始位置对试验弹所受电磁力的影响，定义触发位置s为驱动线圈尾部到电枢尾部的距离。

在充电电压为8 kV、充电电容为1.2 mF时，分析s=50，45，40，35，30 mm时的加速性能。利用图5所示的仿真模型，通过仿真得到不同触发位置下试验弹所受电磁力和试验弹速度随时间的变化曲线，分别如图14、15所示。

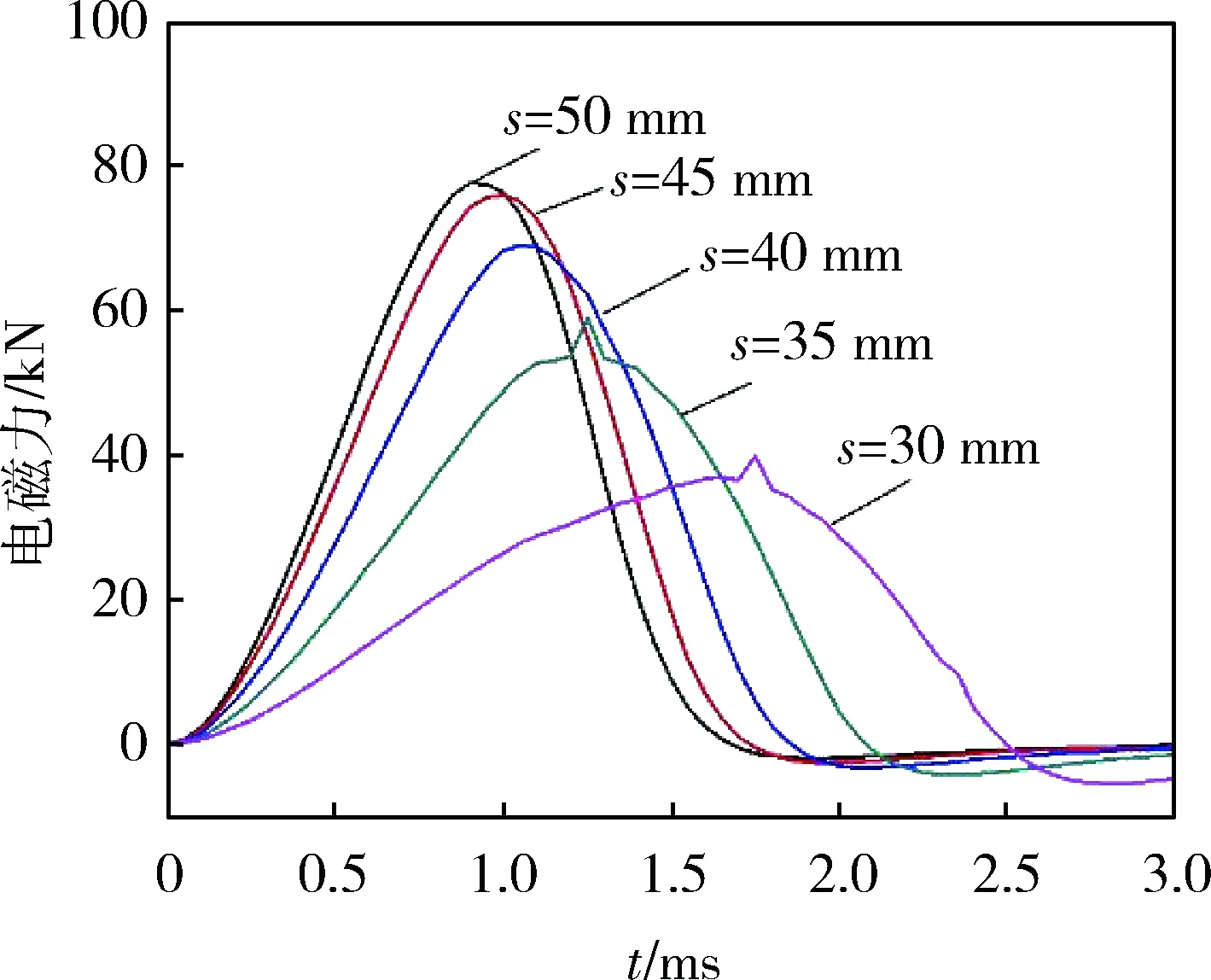
图14 不同触发位置下试验弹所受电磁力 随时间的变化曲线

图15 不同触发位置下试验弹速度 随时间的变化曲线

从图14可以看出：随着试验弹初始位置的变化，其受到的电磁力也发生了相应变化,当s=30 mm时，试验弹受到的电磁力在1.75 ms时达到最大值39.9 kN；当s=35 mm时，试验弹受到的电磁力在1.25 ms时达到最大值59.1 kN；当s=40 mm时，试验弹受到的电磁力在1.05 ms时达到最大值68.9 kN；当s=45 mm时，试验弹受到的电磁力在1 ms时达到最大值76 kN；当s=50 mm时，试验弹受到的电磁力在0.9 ms时达到最大值77.7 kN。可见：随着驱动线圈尾部和电枢尾部之间距离的增大，试验弹受到的电磁力峰值在逐渐增大，但是峰值的持续时间在逐渐缩短；同时，随着s的增大，电磁力的上升和下降时间也将缩短。因此，要延长电磁力峰值的持续时间，也可以通过调整试验弹和驱动线圈之间的相对位置来实现。

从图15可以看出：试验弹初始位置的变化，不仅使驱动线圈的放电电流和试验弹受到的电磁力发生了变化，同样使试验弹的发射速度发生了变化，当s=30 mm时，试验弹在2.5 ms时达到最大速度86.7 m/s；当s=35 mm时，试验弹在2.1 ms时达到最大速度101 m/s；当s=40 mm时，试验弹在1.85 ms时达到最大速度107.8 m/s；当s=45 mm时，试验弹在1.75 ms时达到最大速度109 m/s；当s=50 mm时，试验弹在1.7 ms时达到最大速度105.7 m/s。

5 结论

电磁线圈发射技术作为一种新的驱动技术应用到引信模拟试验中，具有明显的优势。对于不同的引信，通过调整充电电压、电容和触发位置，能够精确控制试验弹受力和加速时间，使其符合所模拟引信的要求，实现了一套设备模拟多种不同类型引信的需求。研究结果将为后期单级或多级电磁线圈发射技术在引信模拟试验中的应用提供指导。

[1] 张景玲，纪永祥. 引信试验鉴定技术[M]. 北京: 国防工业出版社, 2006: 214-215.

[2] 齐杏林，杨清熙. 基于气体炮的引信动态模拟方法综述[J]. 探测与控制学报, 2011, 33(6): 1-4.

[3] 杨清熙，齐杏林，赵志宁，等. 撞击减速法模拟引信后坐加速度的影响因素[J]. 弹箭与制导学报, 2012, 32(3): 111-117.

[4] 范安乐，唐晓峰. 引信试验用模拟火箭弹[J]. 探测与控制学报, 2008, 30(3): 29-36.

[5] Andrews J A. Coilgun Structures[J]. IEEE Transactions on Magnetics, 1993, 29(1): 637-642.

[6] Mcnab R. Electric Gun Research[J]. IEEE Transactions on Magnetics, 1999, 35(1): 250-261.

[7] 王莹.电发射技术概论[J].电工技术杂志,2003(10):94-98.

[8] 邹本贵，曹延杰. 美军电磁线圈发射技术发展综述[J]. 微电机, 2011, 44(1): 86-89.

[9] 赵博, 张洪亮. Ansoft 12在工程电磁场中的应用[M]. 北京: 中国水利水电出版社, 2010:33-35.

[10] 赵科义，李治源，程树康. 单级感应线圈炮工作过程的动态仿真[J]. 高电压技术, 2008, 35(8): 1667-1671.

(责任编辑:尚彩娟)

Research on Fuze Dynamic Simulation Based onElectromagnetic Coil Launcher

ZHAN Chao, XIANG Hong-jun, LEI Bin

(Department of Ammunition Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)

Aiming at the limitations of traditional simulation test methods in fuze, the application of electromagnetic launch technology on the fuze simulation test is proposed. The fundamental constitution and working principle are elaborated, and the mathematical model of the working process is established. Through the simulation and analysis, feasibility of fuze test with electromagnetic launch technology is validated. The influence of the charging voltage, the capacitance and the trigger position on the force and speed are analyzed. The results show that: the force of the tested projectile can be changed according to the requirements of simulation of fuze by adjusting those parameters.

electromagnetic drive; fuze; dynamic simulation

1672-1497(2015)02-0056-05

2015-01-04

军队科研计划项目

詹 超(1991-)，男，硕士研究生。

TJ430.6+8

A

10.3969/j.issn.1672-1497.2015.02.011