固态发酵罐热－固耦合应力及强度分析*

薛晓宁，赖祥彬，张 建，刘 林，石 凯，曾 涛

(广东海洋大学工程学院，广东湛江 524000)

0 引言

固态发酵(Solid State Fermentation)，是指微生物在没有或基本没有游离水的固态湿培养基上生长、繁殖、代谢的发酵过程，发酵设备必须满足微生物生长环境和发酵工艺的要求，固态发酵设备是目前制约固态发酵技术生产应用的主要瓶颈［1］，发酵罐是发酵设备的核心功能装置，本研究设计的发酵罐能完成发酵物料的在位加湿混合、高温灭菌、降温冷却、自动接种，可对发酵环境的温度、湿度、空气和二氧化碳含量等发酵过程参数进行检测，传热传质得到强化，可为饲料、中药、生物肥等行业菌种筛选、发酵工艺优化、传热传质和过程检测、控制的试验研究及生产工艺制订提供装置平台。

发酵罐属中低压压力容器，工作时必须对罐体、管路系统清洗、灭菌，还需对发酵原料灭菌、冷却，罐体内部、夹套中的温度、压力变化剧烈，罐体上接口又很多，对罐体结构强度进行研究十分重要。发酵罐主要承受内部压力、温度载荷，在ANSYS中应力与温度可直接耦合分析［2］，因此，笔者在罐体结构设计的基础上，利用有限元对发酵罐进行热－应力耦合应力分析，确定罐体整体及其危险部位，为发酵罐设计提供技术依据。

1 发酵罐设计要求、结构及参数

(1)设计要求 本文以课题已研制的发酵罐样机的罐体为分析对象，发酵罐为搅拌器卧式结构，罐体带热交换外夹套，设有安全通气阀、接种口、进料口、取样口、视镜等;罐体全容积80 L，装料系数小于50%。罐体工作参数:罐内与夹套设计压力≤0.27 MPa，罐内最高温度155℃，夹套内最高温度165℃，夹套冷却水温度在+8℃ ～16℃范围。

(2)发酵罐结构 设计的发酵罐结构如图1，罐体proe模型如图2，主要结构参数如表1。

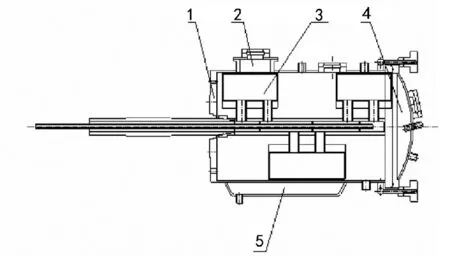
图1 发酵罐整体结构图

图2 罐体有限元分析Proe模型

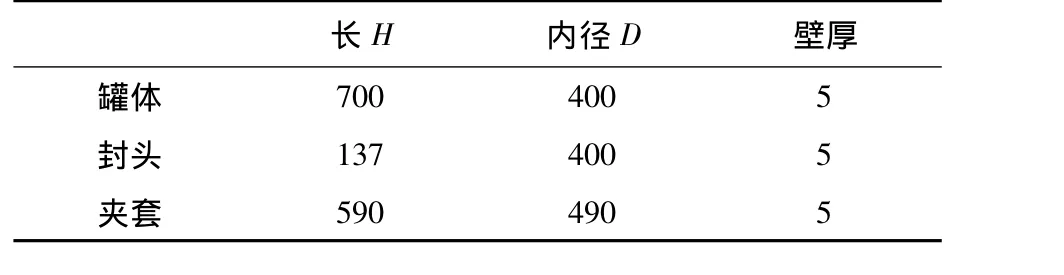
表1 罐体主要结构参数 /mm

(3)材料参数 罐体材料选用316不锈钢，密度7980 kg·m－3，杨氏模量199 GPa，泊松比0.3，膨胀系数17.06，导热系数15.21。

2 发酵罐强度评定依据

根据文献［3］可知:当压力容器在高于常温低于蠕变温度下工作时，其强度指标可按当前温度下的强度极限、屈服极限确定。

本研究中最高的蒸汽温度为165℃，远超出常温，但远低于奥氏体不锈钢的蠕变温度约550℃［4］，故其强度指标按工作温度下的强度极限σb、屈服极限σs确定，由文献［5］查得0Cr17Ni12Mo2(316不锈钢)在165 ℃下的 σs=157.4 MPa，σb=447.5 MPa，高屈强比合金钢安全系数可取为ns=1.5，nb=2.6～3.0［6］。

发酵罐的强度评定可采用第三强度理论［4］:

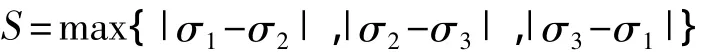
式中:S为应力强度;σ1、σ2、σ3为分别为第一、二和三主应力。

根据 JB4732－95钢制压力容器设计标准规定［4］:设Sm为设计应力强度，k为载荷组合系数，根据发酵罐载荷情况，取k=1;一次总体薄膜应力强度Pm应不超过设计许用应力强度kSm，即Pm≤Sm;一次局部薄膜应力强度Pl，应不超过设计许用应力强度1.5kSm，即 Pl≤1.5Sm;一次薄膜加一次弯曲应力强度Pl+Pb，应不超过设计许用应力强度1.5 kSm，即 Pl+Pb≤1.5Sm;一次应力加二次应力强度 Pl+Pb+Q，应不超过设计许用应力强度3Sm，即Pl+Pb+Q≤3Sm。

根据发酵罐实际受载情况，本研究中按Pl+Pb+Q≤3Sm评定强度，许用应力强度Sm=σs=157.4 MPa。

3 罐体分析

3.1 罐体结构建模

罐体结构及参数如前所述，发酵罐主要承受的载荷为内部压力、温度载荷，故采用热－应力耦合方式分析。罐体在整体结构分析时暂不考虑焊缝等局部结构，而将其看成一个完整结构，这样处理的目的在于找到整个罐体结构的总体应力、应变分布情况，为进一步细化分析做准备，如图3所示，发酵罐属对称结构，取发酵罐结构的1/2建立分析模型。

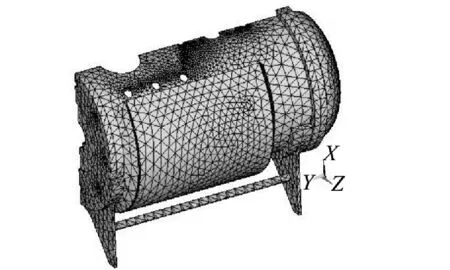
图3 分析模型与网格划分

3.2 分析过程与结果

(1)选择单元类型［2］

单元类型的选择关系到分析结构的精确度及分析结果的可靠性，本文中选用Solid226单元类型，为20节点的六面体单元，每个节点有四个自由度，分别为 UX，UY，UZ，TEMP，满足发酵罐模拟分析要求。

(2)网格划分［2］

单元类型选择coupled－field brick 20 node226，参数按前述定义数据，将proe模型导入有限元分析，将参数导入各个零件中，划分网格，在罐体开口处应力集中比较大，此处网格应比较密集，网格划分结果如图3所示。

(3)载荷约束施加及求解［2］

在对称剖分面上施加对称约束，在支架脚的面上施加UX向的约束(支架起支撑作用)，在罐体及封头内表面上施加一个P=0.27 MPa，t=155℃的约束，在夹套内部各个面上施加一个P=0.27 MPa，t=165℃的约束，计算求解，得到分析结果。

(4)分析结果

图4为整个罐体的总应力云图，图5为罐体应变云图，图6为罐体与夹套焊接处延路径的应力、应变分布。

图4 罐体整体结构总应力分布

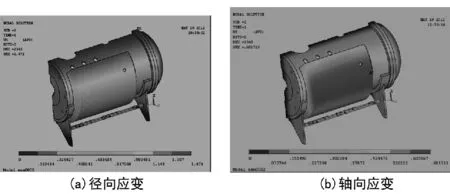
图5 罐体应变云图

图6 罐体与夹套焊接处路径应力应变分布

3.3 结果分析与强度评估

由图4、图5、图6以及罐体分部件应力云图的分析结果知，罐体总体的最大应力为357 MPa，根据在160℃的材料屈服极限158.6 MPa，该应力已大于屈服极限，但根据文献［3］可知，此处结构中会产生二次应力，其许用应力δm≤3［σ］，所以罐体结构安全。

罐体的整体的应力较大区域主要集中在罐体与夹套焊合后的内、外承压区、高温区;A区域应力值偏大，由于结构不连续B区域应力值也很大;由图5的分析结果表明，在径向、环向和轴向应变中径向膨胀部位的径向应变最大;因此，在做进一步细化分析时，重点考察危险区域上的零件、径向应变偏大的部位;由图6所示的A－B路径应力应变分布曲线图可知，应力、应变主要集中在夹套顶部与罐体相互焊接的位置，此处为整体结构的危险部位。

图4所示A区域应力较大，故选取A区域进行强度评估。由有限元计算结果，根据第三强度理论:S=max{|σ1－σ2|，|σ2－σ3|，|σ3－σ1|}=254 MPa，此处结构应力值为一次应力加二次应力强度Pl+Pb+Q，许用极限为3Sm=472.2 MPa，即 S≤3Sm［4］，结构强度安全。

4 夹套分析

4.1 分析过程［2］

(1)建立有限元模型

夹套与罐体焊合为一体，建立夹套的分析模型。

(2)单元类型的选择

选取单元类型Solid226热固耦合场单元，参数设定按前述取值，采用smartsize网格划分形式划分网格，结果如图7(a)。

(3)施加载荷约束及求解［6－8］

在夹套、罐体的内表面加载P=0.27 MPa的压力，在法兰端施加UX、UZ、UY向的约束，前盖焊接端施加UY约束。定义初始零应力温度为20℃，在罐体内部表面上155℃，在夹套四周加载165℃温度载荷，然后分析求解，得到分析结果，图7为夹套沿罐体轴向路径的应力、应变分布。

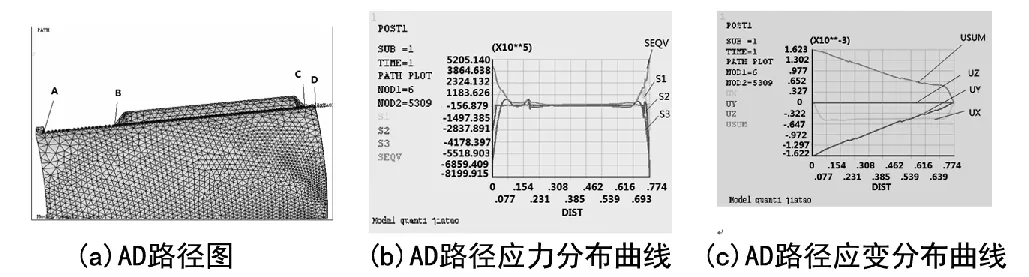
图7 夹套沿罐体轴向路径应力应变分布

4.2 结果分析与强度评估

由夹套应力分析云图可知，夹套上最大应力为294 MPa，根据在160℃的材料屈服极限158.6 MPa，该应力已大于屈服极限，但根据文献［3］可知，此处结构中会产生二次应力，其许用应力δm≤3［σ］，所以该处结构在安全范围;在法兰焊接、前端盖处的局部位置的应力在586～733 MPa之间，由文献［3］可知，采用塑性分析法时在结构不连续处产生的一次和二次应力之和可以大于3［σ］，但三个主应力之和则必须小于4［σ］，故此处结构安全。

根据第三强度理论计算可得应力强度S=|σ1－σ2|=454 MPa，此处结构应力许用值［4］为 S=Pl+Pb+Q≤3Sm=472.2 MPa，可知结构强度安全。观察AD路径应力应变分布曲线，可知应力主要集中在A、B、C、D四点，应变主要集中在AB段。

5 罐体接管开口处分析

由于发酵罐罐体接口多，开孔大，加剧了开孔边缘的应力集中，导致结构不连续，削弱了整体结构的强度，应力集中不仅与开孔有关，还与开孔部位的变形协调有很大关系［8］，对罐体开口进行分析是关键，重点分析罐体接管开口相贯线处的应力、应变。

5.1 分析过程［2］

(1)建立有限元模型

考虑到前端盖与罐体的壁厚尺寸相差大，对罐体应力、应变影响大，将前端盖与罐体建立整体模型，其为对称结构，取接口1/2建模。

(2)划分网格

开口接管处应力比较集中，故应加大此处的网格密度，网格划分的结果如图8(a)。

施加载荷约束［9］在法兰连接处约束 UX，UY，UZ自由度，在前盖上约束UY自由度，在罐体的内部及外部夹套安装部分和前盖内侧上施加P=0.27 MPa的压力，在罐体内部及前盖内侧施加TEMP=155℃，在罐体外部夹套安装部分施加TEMP=165℃，分析计算得到结果，罐体接管开口内侧相贯线应力应变分布如图8所示。

图8 罐体接管开口内侧相贯线应力应变分布

5.2 结果分析与强度评估

在开口接管过渡处的最大应力为536 MPa，根据其载荷形式可知存在二次应力，此处应力允许大于3［δ］，但三个主应力之和应小于4［σ］，依据应力云图，此处结构在安全范围。在开口接管过渡处其应力局部达到516 MPa，根据文献［9］，在应力最大处向周围延伸不大于的区域属于局部应力，R为罐体内壁与外壁半径的中半径，δ为该处最小壁厚，在Ansys中测量，该局部范围为17 mm，故此处属于局部应力，在接口与罐体连接的边缘处最大应力达到1 610 MPa，在实际结构中通过圆角或倒角过渡等结构优化、焊接工艺优化，可使该应力值大幅下降。接管过渡处的应力分为总体薄膜应力、局部薄膜及弯曲应力，前两种必须在设计必须考虑，而弯曲应力主要为二次应力，二次应力在不循环加载的情况下，对结构安全是不会造成影响的，在接管处存在的主要为弯曲应力，包括压力载荷、热载荷产生的弯曲应力，故接管连接处结构安全。由三个主应力及应变的的分布可知，接管结构处的应力应变主要为环向膨胀，这与理论分析结果相符合。

根据第三强度理论计算整体结构的应力强度为S=|σ3－σ1|=344.8 MPa，该结构中许用应力强度［4］为S=Pl+Pb+Q≤3Sm=472.2 MPa，可知结构安全。

由图8相贯线路径应力应变分布可知，应力、应变主要在B区域明显偏高，主要原因是此处结构的不连续。

6 结语与讨论

(1)本文利用有限元的热固耦合等分析方法对发酵罐整体、危险部位进行了应力、应变分析，确定了应力、应变最大值位置，进行了强度安全性校核，分析结果与实际情况接近。

(2)研究方法及结论对发酵罐强度评估、结构优化、制造具有实际指导意义与借鉴价值，为发酵罐结构优化提供了依据，为进一步研究打下了基础。

(3)在高温下用应变片测发酵罐应变误差大，依据较低温度(约70℃ ～80℃)下的应变测试数据，通过有限元模拟仿真找到发酵罐高温带压工况下的应变，将是进一步开展研究的重点;发酵罐工作过程中温度高、变化大，焊缝应力状态复杂［7］，影响因素多，破坏性大，利用有限元对焊缝进行深入研究十分必要。

［1］ Ashok Pandey.Recent advances in solid－state fermentation［J］.Biochemical Engineering Journal，2009(5):13－18.

［2］ 倪 栋，段 进，徐成久.通用有限元分析ANSYS7.0实例精解［M］.北京:电子工业出版社，2003.

［3］ 范钦珊.压力容器应力分析与强度设计［M］.北京:原子能出版社，1977.

［4］ JB4732－95.钢制压力容器分析设计标准［S］.

［5］ 贺匡国.化工容器及设备简明设计手册［M］.北京:化工工业出版社，2002.

［6］ 陈祝年.焊接工程师手册［M］.北京:机械工业出版社，2002.

［7］ 张 祥，张 涛.基于ANSYS压力容器筒体与平板封头焊缝残余应力有限元分析［J］.焊管，2009，36(5):22－24.

［8］ 徐 岩，郑洪涛，梁海东，等.椭圆形封头大开孔结构强度分析［J］.热能与动力工程，2007，22(4):405－408.

［9］ 林国庆，王茂廷.基于ANSYS软件对压力容器开孔接管区的应力与疲劳分析［J］.轻工机械，2011，29(2):117－119.