W-代数偏序集及其性质

折海芳, 赵 彬

(陕西师范大学 数学与信息科学学院, 陕西 西安 710119)



W-代数偏序集及其性质

折海芳, 赵 彬*

(陕西师范大学 数学与信息科学学院, 陕西 西安 710119)

引入了W-引代数偏序集与强W-代数偏序集的概念。讨论了W-代数偏序集、Exact偏序集以及代数偏序集的关系，证明了W-代数偏序集在保定向并的单的核算子下的像是W-代数偏序集。最后得到了每一点有最小局部基的弱Domain是强W-代数Domain,证明了弱Domain上的Scott连续映射保局部基当且仅当它保Weakly way below关系。

W-代数偏序集； 代数偏序集；Exact偏序集； 弱Domain； 局部基

从20世纪70年代初Scott的开创性工作以来,Domain理论因具有理论计算机科学和数学的双重背景而一直受到诸多学者的关注。对Domain的推广是Domain理论研究的一个重要内容。迄今为止,较为成功的推广是拟连续Domain[1]和Z-连续偏序集[2]。作为Domain的另一推广,2007年Mashburn在文献[3]中引入了Weakly way below关系、Exact偏序集和弱Domain的概念,并讨论了它们的一些基本性质。文献[4]研究了Exact偏序集的乘积和映射性质,并且讨论了Exact偏序集的基。文献[5]讨论连续定向完备偏序集(Dcpo)的特征时引入了局部基的概念,并讨论了由此涉入的一些关系定理。本文在Exact偏序集的基础上应用Weakly way below关系推广了代数偏序集,给出了W-代数偏序集的概念,并讨论了W-代数偏序集与Exact偏序集以及W-代数偏序集与代数偏序集的关系。最后文章讨论了弱Domain的局部基的相关性质。

1 预备知识

定义1[6]设L是偏序集，A⊆L。若∀x∈A,y∈L,y≤x时有y∈A，则称A是下集。若∀x∈A,y∈L,y≥x时有y∈A,则称A是上集。

定义2[6]设L是偏序集，D⊆L。若D≠∅且∀x、y∈D,∃z∈D，使得x、y≤z，则称D是定向子集。若L中任一定向子集的上确界存在，则称L为Dcpo。

定义3[7]设L是偏序集，x、y∈L。若对L中任意定向集D,∨D存在且y≤∨D时∃d∈D,使得x≤d,则称xWay belowy，记为x≪y。记x={u∈L|u≪x},x={u∈L|x≪u}。

定义4[7]设L是偏序集,k∈L。若k≪k，则称k为紧元。记L中全体紧元之集为K(L)。

定义5[7]设L是偏序集。若∀x∈L,x是定向集且x=∨x，则称L是连续偏序集。

命题1[7]设L是连续偏序集，x、z∈L。若x≪z,则∃y∈L，使得x≪y≪z，即≪满足插入性质。

定义6[7]设L是偏序集。若∀x∈L,↓x∩K(L)是定向集且x=∨(↓x∩K(L)),则称L是代数偏序集。

定义7[3]设L是偏序集，x、y∈L。若对L中任意定向集D,∨D存在且y=∨D时∃d∈D，使得x≤d，则称xWeakly way belowy，记为x≪wy。记wx={u∈L|u≪wx},wx={u∈L|x≪wu}。

命题2[3]设L是偏序集，x、y、z∈L,则有:

(1)x≪y⟹x≪wy;

(2)x≪wy⟹x≤y;

(3)x≤y≪wz⟹x≪wz。

注1由上述命题知，wx为下集，但wx一般不是上集(见例2)。

定义8[3]设L是偏序集。若∀x∈L,wx是定向集,且∨wx=x,则称L为Exact偏序集。若L还是Dcpo，则称L为Exact Domain。

命题3设L是偏序集，x、y∈L,则x=∨wx当且仅当xy时∃u∈L，使得u≪wx且uy。

命题4[8]每个连续偏序集都是Exact偏序集。

注2每个代数偏序集都是Exact偏序集。

定义9[3]设L是偏序集，R是L上的二元关系，∀x、y、z∈L。若xRy≤z,∃d∈L，使得zRd时有xRz，则称关系R是Weakly increasing的。

定义10[3]设L是偏序集。若L是Exact Domain，且≪w是Weakly increasing的，则称L是弱Domain。

命题5每个Domain都是弱Domain。

命题6[3]设L是弱Domain，则≪w具有插入性质。

定义11[6]设L是偏序集，p:L→L是映射。若∀x、y∈L，有

(1)x≤y⟹p(x)≤p(y);

(2)p(x)=p(p(x))。

则称p是投射算子。

若p还满足

(3)p(x)≤x(x≤p(x))。

则称p是核(闭包)算子。

定义12[7]设L是偏序集,f:L→L是保序映射。若∀D∈D(L)，且∨D存在，有f(∨D)=∨f(D),则称f是Scott连续映射。

在本文中，D(L)表示L上的所有定向子集。所用而未标注的概念和符号请参考文献[2-3]。

2 W-代数偏序集

定义13设L是偏序集，k∈L。若k≪wk，即∀D∈D(L)，∨D存在且k=∨D时∃d∈D，使得x≤d，则称k为弱紧元。记L中全体弱紧元之集为Kw(L)。

由命题2知，紧元一定是弱紧元，但反之不成立。

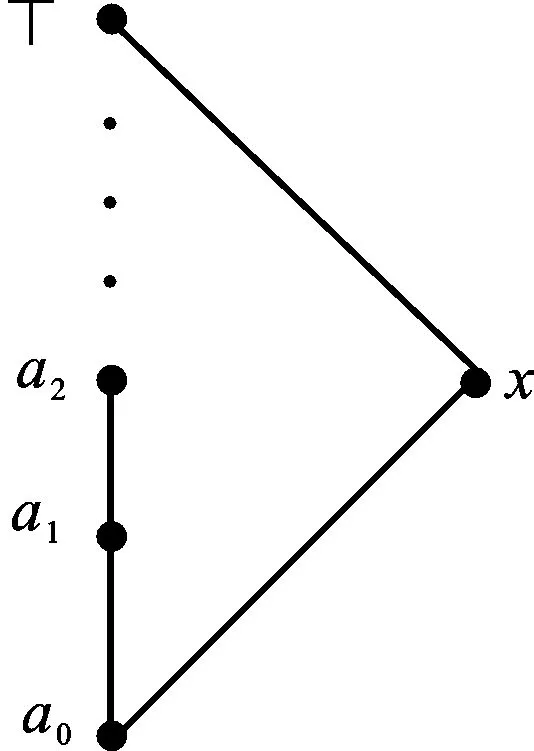
图1 L上的序关系≤Fig.1 Order relation ≤ of L

可以验证x是弱紧元但不是紧元。

命题7设L是偏序集,若∀x∈L,wx是上集，则K(L)=Kw(L)。

证明显然有K(L)⊆Kw(L)。反之，∀x∈Kw(L)，有x≪wx。下证x≪x。∀D∈D(L),x≤∨D。由wx是上集知,x≪w∨D。则∃d∈D,使得x≤d。故x≪x,即x∈K(L)。从而，K(L)=Kw(L)。

定义14设L是完备格。若L满足：

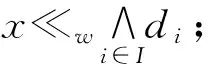
则称L是W-稳定的。

命题8设L是完备格。若L是W-稳定的，则Kw(L)是完备格。

定义15设L是偏序集。若∀x∈L,wx∩Kw(L)是定向集，且x=∨(wx∩Kw(L))，则称L为W-代数偏序集。若≪w还是Weakly increasing的，则称L为强W-代数偏序集。若DcpoL是(强)W-代数偏序集，则称L为(强)W-代数Domain。

上述所定义的W-代数偏序集以及强W-代数偏序集不一定是代数偏序集，见例2。

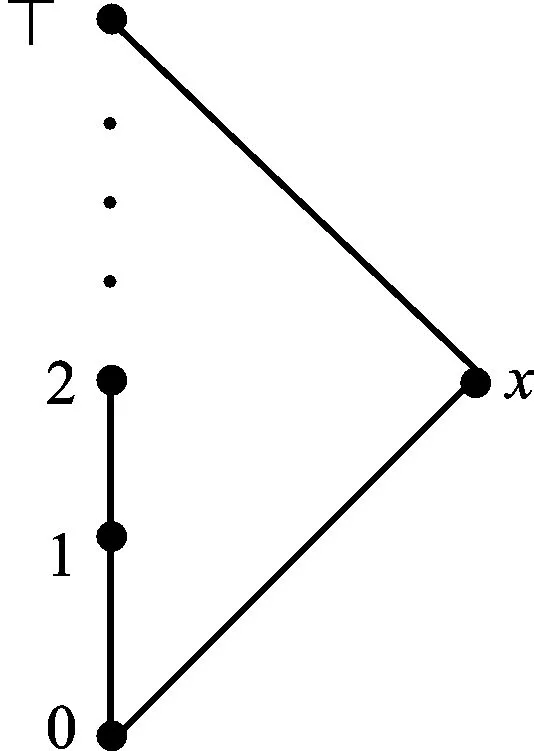
图2 L上的序关系≤Fig.2 Order relation ≤ of L

可以验证，L是(强)W-代数偏序集。由于x不是紧元，故L不是代数偏序集。

(2) 设L=N∪{a,b,c,d}。其中L上的序关系≤如图3所示。

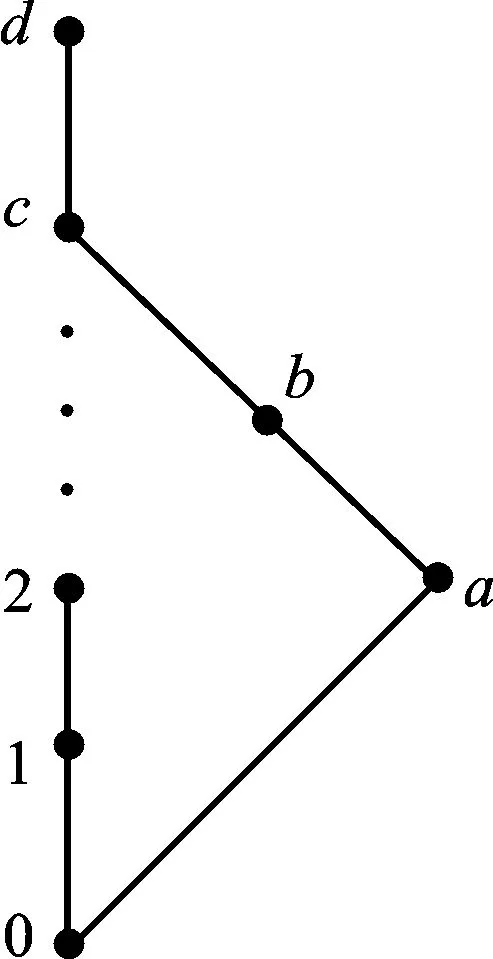
图3 L上的序关系≤Fig.3 Order relation ≤ of L

可以验证，L是W-代数偏序集，且a≪wb≤c≪wd不能推出a≪wc。故L不是强W-代数偏序集，也不是代数偏序集。

命题9设L是偏序集。若∀x∈L，存在定向集D⊆wx∩Kw(L),使得x=∨D,则L是W-代数偏序集。

证明(1)wx∩Kw(L)是定向集。∀a、b∈wx∩Kw(L)，则a≪wa≪wx,b≪wb≪wx。从而有a≪wx,b≪wx。又x=∨D,故∃da、db∈D,使得a≤da,b≤db。又D是定向集，故∃d∈D，使得da、db≤d。又D⊆wx∩Kw(L),故

d∈wx∩Kw(L)且a,b≤d。

(2)x=∨(wx∩Kw(L))。由D⊆wx∩Kw(L)知，∨D≤∨(wx∩Kw(L))。由x=∨D知,x≤∨(wx∩Kw(L))。反之，由于wx∩Kw(L)⊆↓x，则∨(wx∩Kw(L))≤∨↓x=x。故

x=∨(wx∩Kw(L)。

推论1每个代数偏序集都是W-代数偏序集。

证明设L是代数偏序集,则∀x∈L，↓x∩K(L)是定向集，且x=∨(↓x∩K(L))。由命题9知，只需证↓x∩K(L)⊆wx∩Kw(L)。由于∀y∈↓x∩K(L),y≪y≤x,故y≪y≪x,由命题2知

y≪wy≪wx,即y∈wx∩Kw(L)。

命题10设L是偏序集，则L是W-代数偏序集当且仅当L是Exact偏序集，且∀x、y∈L，若x≪wy，则∃k∈Kw(L)使得x≤k≪wy。

证明必要性。首先证明L是Exact偏序集。由L是W-代数偏序集知，∀x∈L,wx∩Kw(L)是定向集且x=∨(wx∩Kw(L))。又因为wx∩Kw(L)⊆wx，故L是Exact偏序集。

其次证明，∀x、y∈L。若x≪wy,则∃k∈Kw(L)使得x≤k≪wy。

由L是W-代数偏序集知，∀y∈L,wy∩Kw(L)是定向集，且y=∨(wy∩Kw(L))。

设x≪wy,则∃k∈wy∩Kw(L),使得x≤k，从而x≤k≪wy且k∈Kw(L)。

k∈wx∩Kw(L),且a、b≤k。

(ⅱ)x=∨(wx∩Kw(L))。显然有∨(wx∩Kw(L))≤x。反之，假设x∨(wx∩Kw(L)),由命题3知，∃u∈L，使得

u≪wx且u∨(wx∩Kw(L))。

由u≪wx以及已知条件知，∃k∈Kw(L)使得u≤k≪wx。从而k∈wx∩Kw(L)且u≤k。所以

u≤k≤∨(wx∩Kw(L)),

矛盾。故x≤∨(wx∩Kw(L))。从而

x=∨(wx∩Kw(L))。

推论2每个强W-代数Domain都是弱Domain。

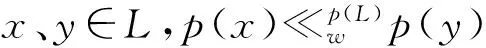
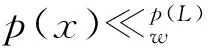
p(y)=p(p(y))=p(∨wp(y))=

p(p(∨wp(y)))=

∨p(L){p(u)|u≪wp(y)},

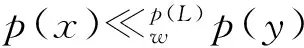
命题12设L是W-代数偏序集,p:L→L是保定向并的投射算子，则Kw(p(L))⊆p(Kw(L))。

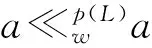
命题13设L是W-代数偏序集，p:L→L是保定向并的单的核算子，则p(L)是W-代数偏序集。

证明设y∈p(L)⊆L,则y∈L。由L是W-代数偏序集知，wy∩Kw(L)是定向集，且y=∨(wy∩Kw(L))。由于p保定向并，故

y=p(y)=p(∨(wy∩Kw(L)))=

∨p(wy∩Kw(L))。

下证p(wy∩Kw(L))⊆。其中

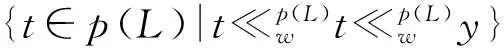
∀t∈p(wy∩Kw(L)),则∃x∈wy∩Kw(L)使得t=p(x),则。由命题11知，。即。∀D∈D(p(L)),t=∨p(L)D,则p(x)=t=p(t)=p(∨p(L)D)。由p是核算子知，∨LD存在且∨p(L)D=∨LD,则p(x)=p(∨LD)。再由p是单的知，x=∨LD。由知，∃d∈D,使得x≤d。从而p(x)≤p(d)=d,即t≤d。故,即

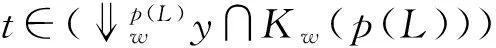
3 弱Domain的局部基

定义16设L是Dcpo，x∈L。若Dx⊆wx,Dx是定向集且∨Dx=x,则称Dx是x的局部基。

命题14设L是Dcpo，则L是Exact偏序集当且仅当∀x∈L,x有局部基。

命题15设L是弱Domain，x∈L，且D⊆wx。则D是x的局部基当且仅当∀y∈wx,∃d∈D,使得y≪wd。

证明必要性。∀y∈wx,由命题6知，∃z∈L使得y≪wz≪wx。又因为D是x的局部基，则x=∨D,所以∃d∈D使得y≪wz≤d≪wx。由≪w是Weakly increasing的知，y≪wd。

充分性。设d1、d2∈D,则d1、d2≪wx。由wx是定向集知，∃d′∈wx使得d1、d2≤d′且d′≪wx，由条件知∃d∈D使得d′≪wd,则d1、d2≤d。从而D是定向集。显然有x=∨wx≤∨D≤x故x=∨D,即D是x的局部基。

命题16设L是弱Domain，x∈L，且D⊆wx。则D是x的局部基当且仅当D是定向集且∀y∈L，若xy，则∃d∈D使得dy。

证明必要性。显然D是定向集。由D是x的局部基知，x=∨D。若xy,则∨Dy。故∃d∈D使得dy;

充分性。只需证x=∨D。由D⊆wx知，∨D≤∨wx=x。反之，假设x∨D，则由条件知∃d∈D使得d∨D，矛盾，故x≤∨D。从而x=∨D。

命题17设L是弱Domain，x∈L,且D⊆wx,则D是x的局部基当且仅当∀y∈L，若y∈wx,则∃d∈D，使得y≤d。

证明必要性。由命题15可知。

充分性。设d1、d2∈D，则d1、d2≪wx。由wx是定向集知,∃d′∈wx，使得d1、d2≤d′。又由条件知∃d∈D使得d′≤d。这时有d1、d2≤d，故D是定向集。显然有x=∨wx≤∨D≤x。故x=∨D,即D是x的局部基。

命题18设L是弱Domain,x∈L。若D是x的最小局部基，则D⊆Kw(L)。

证明由D是x的最小局部基知，D⊆wx。假设∃b∈DKw(L)。下证D{b}也是x的局部基。

∀d1、d2∈D{b},由D是定向集知∃d0∈D使得d1、d2≤d0,再由D是定向集知∃d3∈D使得b、d0≤d3。由命题15知∃d∈D使得d3≪wd。从而d1、d2≤d,b≪wd。故b≠d。所以D{b}是定向集。由D是x的局部基以及命题15知，∃d0∈D使得b≪wd0。且d0∈D{b}。从而x=∨D=∨(D{b}),即x=∨(D{b});

从而D{b}是x的局部基。这与D的最小性矛盾,故D⊆Kw(L)。

推论3设L是弱Domain。若∀x∈L,x有最小局部基，则L是强W-代数Domain。

命题19设L、M是弱Domain，则Scott连续映射f:L→M保局部基当且仅当f保Weakly way below关系。

证明必要性。设x、y∈L且x≪wy,Dy是y的局部基，则由命题15知，∃d∈Dy使得x≪wd。因为f保局部基，所以f(Dy)是f(y)的局部基。则f(d)∈f(Dy)⊆wf(y)。从而

f(x)≤f(d)≪wf(y),则f(x)≪wf(y)。

充分性。设Dx是x的局部基，则Dx⊆wx,x=∨Dx。由连续映射f保Weakly way below关系知，f(Dx)⊆wf(x)且f(Dx)是定向集，且

∨f(Dx)=f(∨Dx)=f(x)。

故f(Dx)是f(x)的局部基，即f保局部基。

4 结语

本文在代数偏序集的基础上,引入了W-代数偏序集的概念,讨论了W-代数偏序集、Exact偏序集以及代数偏序集的关系。最后引入弱Domain的局部基的概念,讨论了局部基的相关性质。这些结果将有利于对保局部基的Scott连续映射的性质展开进一步的研究。

[1] Gierz G, Lawson J D, Stralka A. Quasicontinuous posets[J].Houston Journal of Mathematics, 1983, 9(2): 191-208.

[2] Wright J B, Wagner E G, Thather J W. A uniform approach to inductive posets and inductive closure[J].Theoretical Computer Science, 1978, 7(1): 57-77.

[3] Mashburn J.A comparison of three topologies on ordered sets[J].Topology Proceedings, 2007, 31: 1-21.

[4] 俞挺, 徐晓泉.Exact偏序集的乘积和映射性质[J].江西师范大学学报: 自然科学版, 2008, 32(3): 292-295.

[5] 赵彬, 刘妮.连续domain的特征与浓度[J].陕西师范大学学报: 自然科学版, 2002, 30(2): 1-6.

[6] Davey B A, Priestley H A.Introduction to lattice and order[M].Cambridge:Cambridge University Press,1990.

[7] Gierz G, Hofmann K H, Keimel K, et al.Continuous lattices and domains[M].Cambridge: Cambridge University Press, 2003.

[8] 陈昱.半连续格及相容连续偏序集研究[D].扬州: 扬州大学数学科学学院, 2009.

〔责任编辑 宋轶文〕

W-algebraic poset and its properties

SHE Haifang, ZHAO Bin*

(School of Mathematics and Information Science, Shaanxi Normal University,Xi′an 710119, Shaanxi, China)

The concepts ofW-algebraic poset and strongW-algebraic poset are introduced.The relationship amongW-algebraic poset,Exact poset and algebraic poset is investigated.The image of aW-algebraic poset under an injective kernel operator preserving sups of directed sets isW-algebraic poset.It is shown that it is a strongW-algebraic domain if every point of a weak domain has a minimum local basis.It is also shown that a Scott continuous mapping of a weak domain preserves local basis if and only if it preserves Weakly way below relation.

W-algebraic poset; algebraic poset; Exact poset; weak domain; local basis

06A11, 06B35

1672-4291(2015)03-0013-05

10.15983/j.cnki.jsnu.2015.03.134

2014-09-09

国家自然科学基金资助项目(11171196,11301316); 中央高校基本科研业务费专项资金项目(GK201302003)

折海芳,女,硕士研究生,研究方向为格上拓扑与模糊推理。E-mail: shehaifang123@126.com

*通信作者：赵彬,男,教授,博士生导师。E-mail: zhaobin@snnu.edu.cn

O153.1

A