基于单神经元和前馈补偿的电动加载复合控制

王修岩，谷新铭，李宗帅

（中国民航大学航空自动化学院，天津300300）

电动负载模拟器能够在实验室条件下模拟飞行器飞行过程中所受到的气动载荷，跟随舵机运动并对期望力矩进行加载。作为承载对象的舵机承受负载模拟器施加的加载力矩并进行角位移控制。舵机的主动运动对加载力矩有很强的耦合作用，并影响着加载系统的力矩跟踪精度［1］。所以如何克服由舵机运动产生的多余力矩、提高系统加载精度并保证系统的鲁棒性成为现在电动加载系统要解决的重要问题。

单神经元神经网络的结构简单，自适应能力强，且具有一定的非线性映射能力，运行时间短，收敛速度快，适合在线运行［2］。将单神经元与传统的PID 控制相结合，可以对PID 参数进行在线整定，抗干扰能力强，适合于存在较强位置扰动的电动负载模拟器的控制。

为了进一步提高电动加载系统的收敛速度和跟踪精度，本文提出了用基于扰动因子的自适应粒子群算法和单神经元神经网络复合优化PID参数，从而能显著地改善系统的控制性能。

1 电动负载模拟器控制系统

电动负载模拟系统是一个具有强位置扰动的伺服系统［3］，以转矩为被控量。承载对象舵机进行主动运动，加载系统跟随其运动并对力矩进行加载，所以舵机运动引起的强位置扰动严重影响着加载系统的力矩跟踪性能。

加载对象舵机并非某一固定型号，由于舵机在中低频的力负载刚度大［4］，可以假设其刚度无穷大来简化系统模型，简化后的系统模型如图1所示。

图1 电动加载系统结构图Fig.1 System structure diagram of electric load

选用直流力矩电机为电动负载模拟器的执行元件，系统的动态方程可表示为

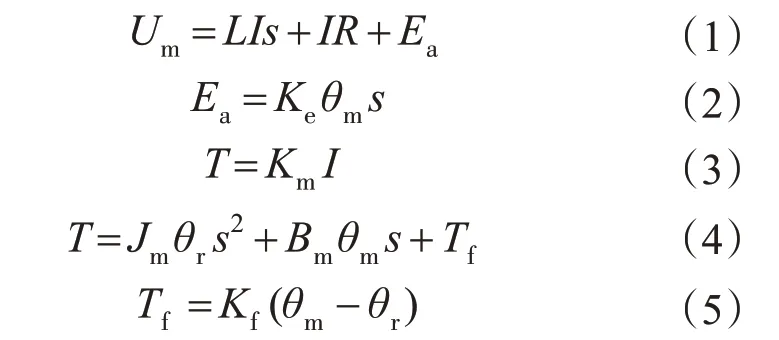
式中：Um为直流力矩电机的电枢电压，V；I为电枢电流，A；R为总回路电阻，Ω；Ea为电机运动产生的反电动势，V；L为回路的等效电感，mH；Ke为电机的反电动势常数，V·s/rad；T为电磁转矩，N·m；Km为电机的转动常数，N·m/A；Jm为转动惯量，kg·m2；Bm为电机的阻尼系数，N·m·s/rad；Kf为连接刚度，N·m/rad；θm为电机的转角；θr为舵机转角。

由式（1）～式（5）可将电动加载系统简化为带有干扰输入θr的单输入单输出系统，表达式为

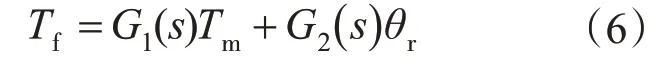
其中

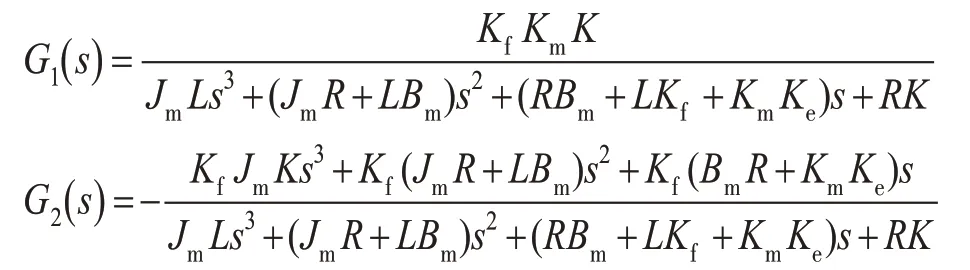
当加载指令力矩输入Tm=0时，系统的力矩输出Tf不为零，此时产生的就是系统多余力矩［5］，如下式所示：

由此可见，舵机的角位移变化使系统产生了多余力矩，相当于给电动加载系统增加了外部扰动。多余力矩超前于加载力矩，并且舵机的扰动频率越高，多余力矩越大，因此要对多余力矩进行抑制来提高系统的加载性能。

2 复合控制系统

用改进的粒子群算法（PSO）优化单神经元PID控制，系统的整体控制结构图见图2。单神经元具有自适应能力，通过改进的粒子群算法优化其权值及系数来适应被控对象的变化，实现参数的自学习，提升单神经元PID控制器的控制效果。

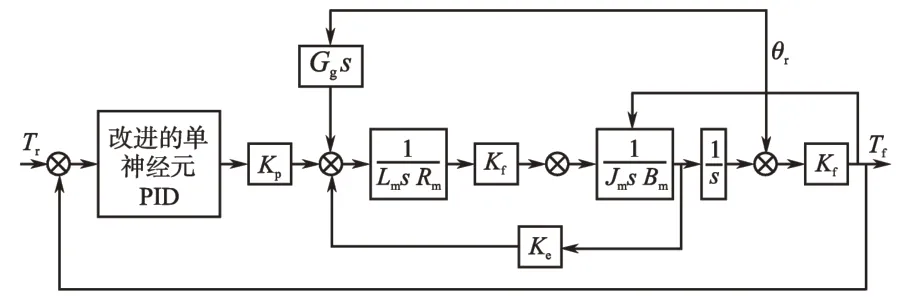
图2 电动负载模拟器复合控制Fig.2 Combined control of electric load simulator

2.1 前馈补偿控制器

在本文中，利用前馈-反馈控制实现对电动负载模拟器的整体控制，前馈补偿实现对舵机位置扰动引起的多余力矩的抑制，闭环负反馈控制是消除干扰引起的小扰动，达到较好的跟踪性能。在电动负载模拟系统中，舵机的主动运动使系统产生了多余力矩，且正比于舵机的角速度。按照前馈补偿对系统多余力矩进行抑制，如图3所示［6］。

图3 速度前馈补偿Fig.3 Feedforward compensation of speed

系统的扰动前馈补偿传函为

1944年底，为逃避武汉大轰炸，全家躲到乡下父亲的朋友家。农历腊月小年这一天，父亲自知挺不过去了，嘱咐家人将他移至小柴房里。当时，姐姐告诉他，汉口大屋被炸毁了。她问父亲：“哪里难过？”父亲回答：“年难过！”父亲死前清醒，不言不语，所有苦难都压在心里，就在小年这天咽的气。

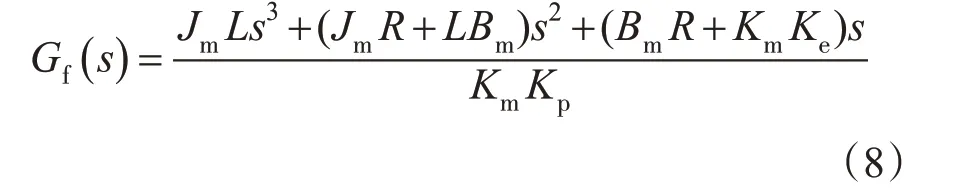
由式（8）可知，多余力矩的大小受舵机的速度、角速度及角加速度的影响。从补偿环节看，分子的阶数比分母高，系统中会引入微分运算，也就引入了系统噪声。为了避免微分噪声环节的存在，引入常数α将式（8）改为以下形式：

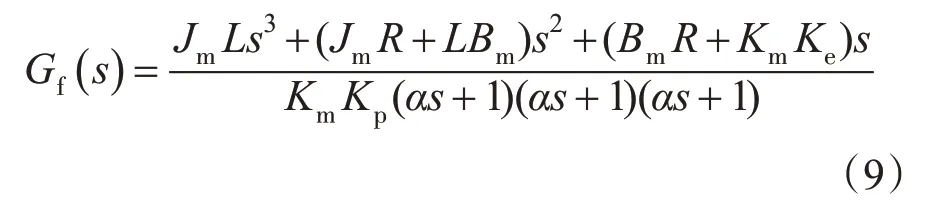
2.2 单神经元自适应PID控制算法

由图4 可以看出，神经网络的3 个权值分别作为了比例、积分、微分系数，在本文中利用改进的PSO 算法优化权值ω和比例系数K 来实现PID控制参数的自适应在线调节，直到控制器稳定。

由文献［7］可知，单神经元有x1，x2，x33 个输入状态变量，其输出为

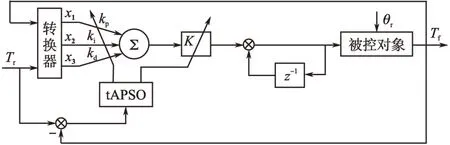
图4 改进PSO优化单神经元PID控制Fig.4 Improved PSO algorithm to optimize the single neuron PID control

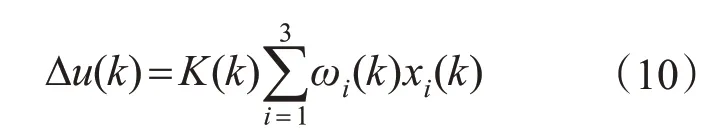
式中：K为神经元的比例系数，为正值。

控制器输出为

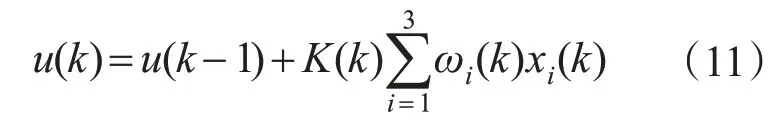
比例系数K对系统的性能产生很大的影响，K越大则系统的快速性越好，但超调量大甚至会导致系统的不稳定；若K很小，系统的响应速度很慢。在本文中，为了调节系统的动静态特性将K设置为一个随系统变化的量。当系统误差大时，K较大，以提高响应速度，使误差尽快减小；误差较小时，K减小，保证系统的稳定性。

2.3 改进的PSO算法优化单神经元PID

单神经元PID的控制过程就是不断优化神经网络的权值，使系统的输出误差不断减小，但是神经网络的权值与目标函数之间是一种非线性的映射关系，采用梯度下降法优化权值其收敛速度慢、精度低，所以，在本文中采用改进的粒子群算法在线优化神经网络的权值和系数的4 维参数，加快电动负载模拟器的收敛速度，改善系统力矩跟踪精度。

2.3.1 扰动因子的引入

基本的粒子群算法在迭代初期搜索速度很快，但是随着迭代次数的增加，容易陷入局部最优。在本文中，采用停滞步数t，ts作为变动条件，加入扰动因子［9］对个体极值和全局极值进行更新，可表示为

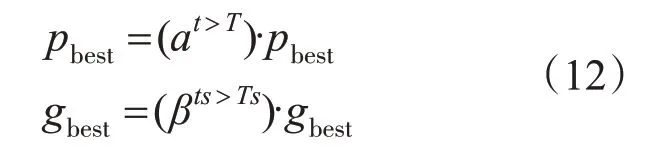
其中

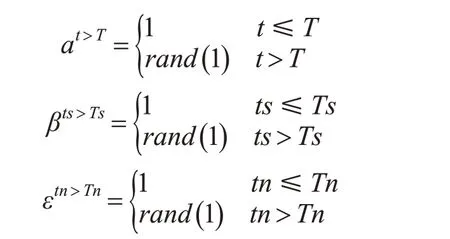
加入扰动因子后PSO 算法的速度和位置更新公式可表示为

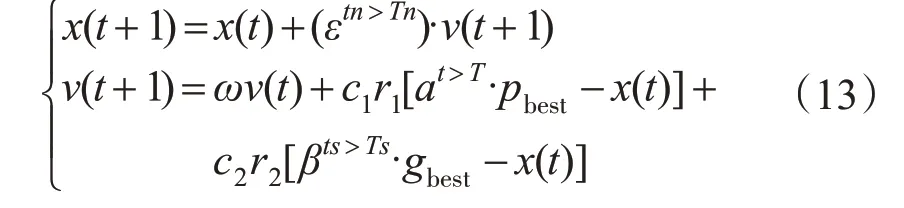
2.3.2 惯性权重ω的调整

惯性权重ω对PSO算法的寻优性能具有重要影响，较大的ω有利于提升全局搜索能力，较小的ω则有利于局部寻优，保证收敛［10］。一般ω的取值范围在［0.4，0.9］之间，本文利用指数来调整惯性因子，利用下式自适应在线更新权重：

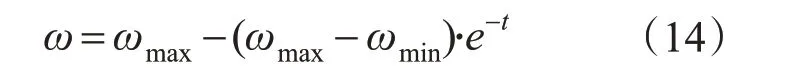
2.3.3 优化目标的选取

选用包含采样时间t 和误差e 的积分性能指标作为优化的目标函数，即

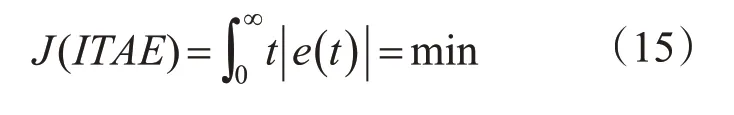
3 仿真及结果验证

根据图1 的电动负载模拟器复合控制结构，通过舵机频率及参数的变化来检验加载系统的性能，利用Matlab2012a对控制系统进行仿真。

3.1 对多余力矩的抑制能力

当系统不加入任何控制时，舵机幅值为±3.5°，频率为1 Hz的正弦信号，此时系统多余力矩如图5a 所示，达到约22 N·m。采用了混合控制策略后，多余力矩得到了不同程度的抑制，如图5b 所示，采用复合控制系统多余力矩降低到了0.03 左右，显示出在复合控制下系统的多余力矩得到了较好的抑制。

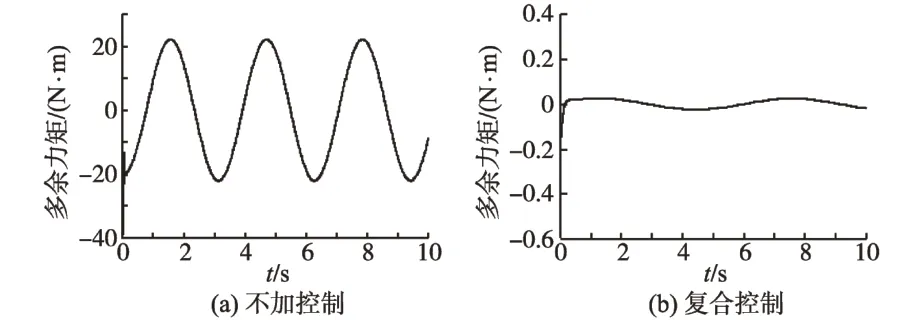
图5 系统多余力矩Fig.5 System extra torque

3.2 动态跟踪能力

电动加载系统的动态跟踪性能【11】是指当有舵机的位置扰动存在时，在不同的加载频率下指令力矩的跟踪情况。给定舵机的扰动信号为幅值±3.5°、频率5 Hz 的正弦信号，指令力矩信号的幅值为±3.5°，图6a 和6b 分别为加载频率5 Hz 和10 Hz时加载力矩跟踪情况。由图6 的力矩误差跟踪曲线可以看出，当加载频率分别为5 Hz 和10 Hz时，复合控制的跟踪精度远大于传统的PID控制，由此可以看出在该复合控制下电动负载模拟器有较好的动态跟踪性能，但是随着加载频率的增大跟踪进度略有下降。

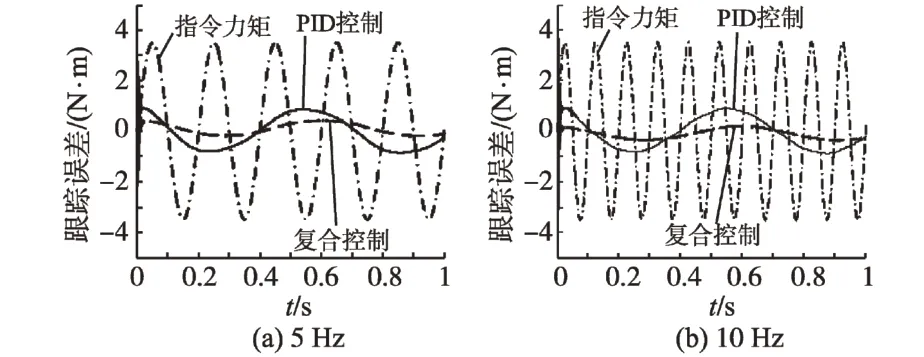
图6 跟踪误差Fig.6 Tracking error

3.3 系统的鲁棒性

由于电动加载系统的强耦合性存在，承载舵机的变化对控制性能有重要的影响。在指令力矩为0，舵机的信号频率分别为1 Hz和10 Hz的情况下，系统的等效转动惯量由0.04 kg·m2变为0.4 kg·m2，阻值由7.5 Ω变为2 Ω时，变化前后的多余力矩如图7、图8所示。当频率为1 Hz时，两种控制策略下多余力矩的变化都不是很大，当扰动频率为10 Hz 时，PID 控制前后多余力矩变化了1.5 N·m，而复合控制下多余力矩变化很小，说明了该复合控制方法能较好地适应参数变化并抑制多余力矩。

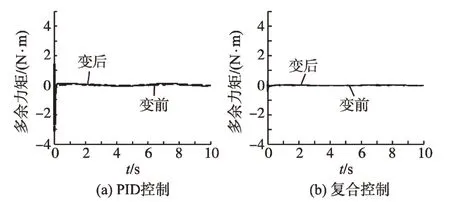
图7 1 Hz时两种控制下的多余力矩Fig.7 Two under the control surplus torque in 1 Hz

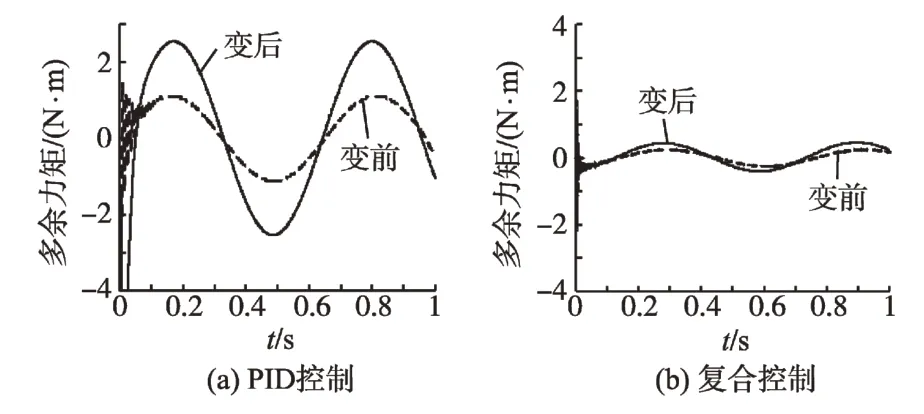
图8 10 Hz时两种控制下的多余力矩Fig.8 Two under the control surplus torque in 10 Hz

4 结论

本文提出了一个电动负载模拟器的多余力矩抑制和加载力矩的跟踪的复合控制方法。该方法通过前馈补偿实现对电动加载系统舵机位置干扰的抑制，并用基于扰动因子的粒子群算法在线更新单神经元PID参数实现反馈控制减小加载力矩的跟踪误差。通过与传统PID 控制相比较，验证了该复合控制的有效性。结果表明，基于扰动因子的粒子群算法实现了多余力矩的抑制，大大减小了加载力矩的跟踪误差，并对系统参数变化有较好的鲁棒性能。

［1］ 韩红业.舵机电动加载控制系统设计与仿真［D］.西安：西北工业大学，2007.

［2］ 李俊丽，何勇，王生泽.单神经元PID 在多电机同步控制中的应用［J］.机电工程，2010，27（8）：14-63.

［3］ 朱伟.电动负载模拟器控制方法研究［D］.西安：西北工业大学，2005.

［4］ 苏东海，刘峰，王洁.被动式加载系统多余力矩的本质特征分析［J］.沈阳工业大学学报，2001，23（6）：449-451.

［5］ 司丹丹，赵晓蓓，符文星，等.应用多路前馈和负反馈提高电动加载系统性能研究［J］.测控技术，2008，27（5）：90-93.

［6］ Rodic M，Jezemik K，Triep K.Dynamic Emulation of Mechanical Loads：an Advanced Approach［J］.IEEE Electric Power Applications，2006，153（2）：159-166.

［7］ 李书舟，容慧.单神经元自适应PID算法在无刷直流电机控制系统上的应用研究［J］.自动化与仪器仪表，2014（4）：44-46.

［8］ kennedy J，Eberhart R.Particle Swarm Optimization［C］//IEEE Intermational Conference on Neural Networks.Perth，1995：1942-1948.

［9］ 赵志刚，张振文，石辉磊.带扰动因子的自适应粒子群算法［J］.计算机科学，2013，40（12）：68-103.

［10］冯冬青，邢广成，费敏锐，等.基于改进PSO 算法的多变量PID 型神经网络控制［J］.系统仿真学报，2011，23（2）：363-385.

［11］王超.电动负载模拟器设计与研究［D］.哈尔滨：哈尔滨工业大学，2010.