4种三电平载波调制策略对比研究

李宁，王跃，王兆安，张辉

（1.西安理工大学自动化与信息工程学院，陕西 西安710048；2.西安交通大学电气工程学院，陕西 西安710049）

三电平中点钳位（neutral point clamped，NPC）变流器具有输出功率大、输出波形THD小、器件电压应力和系统EMI低等多方面的优点［1-5］，因而被广泛地应用于高压大功率场合。

如图1 所示为三电平NPC 变流器主电路拓扑，其中Udc为直流总电压，C1，C2为直流电容，Sa1—Sa4、Sb1—Sb4和Sc1—Sc4为三相功率器件，VD1—VD6为钳位二极管，Ua，Ub，Uc为变流器侧输出相电压，ia，ib，ic为变流器侧输出相电流，io为直流电容中点电流，P，O，N为相电压输出的3种状态。

图1 三电平NPC变流器主电路拓扑图Fig.1 Main circuit topology of NPC three-level converter

调制策略是三电平NPC 变流器的一项关键技术，也是研究热点和难点。目前存在多种三电平调制策略，载波调制策略［6-7］（carrier-based PWM strategy）是应用十分广泛的其中一种。如图2 所示为三电平NPC 变流器传统载波调制策略示意图，图2 中Urx为x（x=a，b，c）相调制波，Uc1和Uc2为上下载波。由于载波所在区域之间不存在公共部分，这种策略被称为载波层叠策略。根据载波层叠策略中载波之间的相位关系，又可以将载波层叠策略分为2 种：1）载波同相层叠策略（PD-PWM）——上下2 个载波的相位相同，如图2a 所示；2）载波反相层叠策略（POD-PWM）——上下2 个载波的相位相反，如图2b所示。

图2 2种三电平载波层叠调制策略示意图Fig.2 Schematic diagram of two kinds of three-level carrier cascading PWM strategy

近年来的研究发现载波之间的偏移关系可影响调制策略的性能，因而产生了载波交叠调制（COPWM）策略［8-13］，具体如图3 所示。其中Urx，Uc1和Uc2为x相调制波和载波，V为载波宽度的标幺值（V＞1），根据载波交叠策略中载波之间的相位关系，也可以将载波交叠策略分为同相交叠策略（COPWM-A）和反相交叠策略（COPWM-B），如图3a和图3b所示。

图3 2种三电平载波交叠调制策略示意图Fig.3 Schematic diagram of two kinds of three-level carrier overlapping PWM strategy

本文针对上文提到的4 种调制策略，通过3方面的性能对其进行对比研究：1）4 种策略对中点电压波动的影响；2）4 种策略输出波形的基波幅值；3）4种策略输出波形的THD特性。

1 4种策略对电容电压的影响

中点电压波动问题是NPC 变流器的固有问题，现有研究表明：中点电压波动正比于中点电流波动［14-16］，下文将通过对4 种调制策略对中点电流的影响分析调制策略对电容电压的影响。

1.1 应用载波层叠法时中点电流io的表达式

三电平NPC 变流器中点电流由3部分组成，如下式所示：

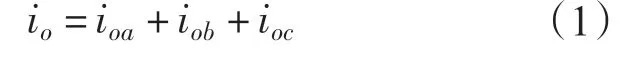
式中：iox为由x（x=a，b，c）相电流引起的中点电流。

当采用载波层叠法时，iox与相电流的关系可表示为

式中：Urx为x相参考电压标幺值。

将式（2）带入式（1）有：

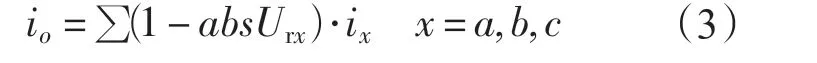
在三相3线系统中，存在如下关系：

据此可以得到中点电流io在1个工频周期内的分段表达式，具体如下式所示：

式中：M为系统的调制度；I为相电流峰值；φ 为功率因数角；ω 为系统角频率。

根据式（5）可求得一个工频周期内中点电流的最大值与参数的关系，如下式所示：

1.2 采用载波交叠法时中点电流io的表达式

当调制策略为载波交叠法时，中点电流iox的表达式为

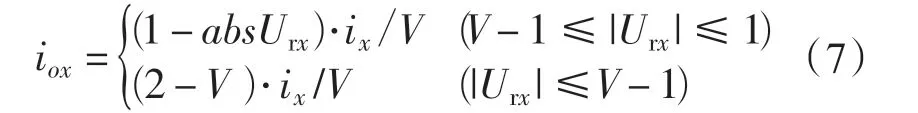
将式（7）带入式（1）可以得到应用载波交叠法时的中点电流io的表达式。该表达式受三相调制波与V 关系的影响，其表达式和一个工频周期中的最值表达式十分复杂，这里不一一列举。

如图4 所示为在调制度M、功率因数角φ 相同而载波幅度V值不同的情况下载波交叠法和载波层叠法产生的中点电压波动的峰值比，由图4可知：1）在相同的情况（M，φ）下，载波交叠法的中点电压波动峰值至多是载波层叠法的1/V；2）如果M≤V，载波交叠法不引起中点电压的波动；3）如果M＞V，载波交叠法与载波层叠法所产生的中点电压波动峰值比受M 和φ 的影响，M 值越小，比值越小，φ 值越大，比值越小。

图4 载波交叠法与载波层叠法产生的中点电压波动峰值比Fig.4 The ratio of the NP potential fluctuation peak value between COPWM-A（COPWM-B）and POD（PD）

2 4种策略对输出波形的影响

为了研究4种策略输出脉冲的THD特性，应用双重傅里叶级数对输出相电压脉冲进行傅里叶分析［17］，双重傅里叶级数的展开式及各项系数分别如下式所示：

式中：ωs为调制波频率；ωc为载波频率。

在求解各项系数时，经常需求解形如cos(ξ cos θ)，sin(ξ cos θ)等包含另一个三角变量的三角函数的积分，此时可利用下式的雅克比-安格尔将其展开成贝塞尔级数形式［17］。

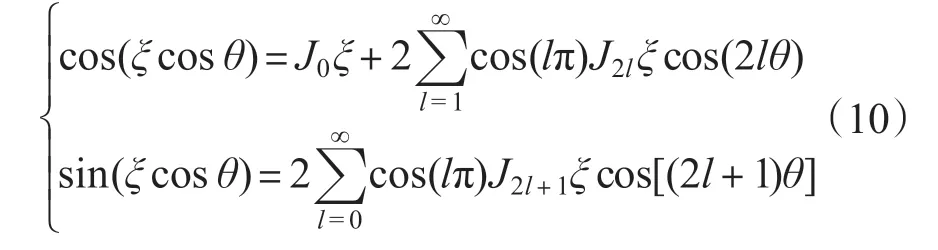
2.1 载波层叠法的输出THD分析

根据式（8）～式（10），可以推导出三电平载波同相层叠法输出的相电压和线电压的表达式，输出相电压傅里叶级数各项系数及输出线电压傅里叶级数各项系数如下：

同理推导出三电平载波反相层叠法输出的相电压和线电压脉冲傅里叶级数各项系数，见下式：

2.2 载波交叠法的输出THD分析

当采用载波交叠策略时，类似于上文的分析也可以推导出载波同相交叠和载波反相交叠法输出相电压和线电压的表达式，这里不一一赘述。经过本文的分析和推导可得4种载波调制策略输出的相电压和线电压所含成分，具体如表1和表2所示。图5给出了理论情况下载波交叠法与载波层叠法输出电压的基波幅值之比。

表1 4种调制输出相电压对比Tab.1 Phase voltage comparison of 4 kinds PWM strategy

表2 4 种调制输出线电压对比Tab.2 Line voltage comparison of 4 kinds PWM strategy

图5 载波交叠法与载波层叠法输出电压基波幅值比Fig.5 The fundamental amplitude ratio between COPWM-A（COPWM-B）and PD-PWM（POD-PWM）

根据表1、表2和图5可知：

1）4 种策略输出电压相位与调制波相位相同，载波层叠法的基波幅值与调制波幅值相同，载波交叠法的基波幅值受载波宽度V和调制度M的双重影响，在同一载波宽度下，载波交叠法的基波幅值随M 的增大而减小；在同一调制度下，当M较小（M＜0.7）时，载波交叠法的基波幅值随V的增加而增加，当M较大（M＞0.7）时，载波交叠法的基波幅值随V的增加而减小。

2）4种策略输出相电压中的谐波分量为基波倍频分量、载波倍频分量和边带谐波分量，其中2种层叠策略输出相电压的基波倍频分量为零，2种交叠策略输出相电压中含有奇数次基波倍频分量；两种反相策略输出相电压的载波倍频分量为零，只含有n为奇数次的边带谐波；2种同相策略输出相电压中包含奇数次载波倍频分量和m+n为奇数次的边带谐波。

3）4 种载波调制策略的输出线电压中的谐波分量为基波倍频分量和边带谐波分量，其中2种层叠策略输出线电压的基波倍频分量为零，只含m+n 为奇数且n 不为3 的倍数次的边带谐波，2 种交叠策略输出相电压中包含6k±1 次的基波倍频分量和n 为奇数而非3 的倍数次的边带谐波。

3 实验验证

为了验证本文分析的正确性，搭建了三电平NPC 逆变器平台进行实验验证。采用DSP+FPGA控制整个系统。直流侧电容值为2 000 μF，直流侧电压为100 V，负载侧滤波器采用LCL 结构（3 mH，17 μF和3 mH），实验负载为阻性负载，阻值为50 Ω，系统的等效开关频率为2 kHz。

图6～图9 分别为采用载波层叠调制策略（M=0.8）和载波交叠调制策略（M=0.8，V=1.6）时输出相电压（以直流侧中点为基准）和线电压的脉冲波、中点电压的波动情况和滤波后的线电压波形及各实验结果的FFT 分析，表3～表6 为实验结果对比。

图6～图9和表3～表6证明了前文分析的正确性，同时还可得到如下结论：1）不同调制策略引起的中点电压波动交流分量中，最主要的成分是3 次谐波，这是由于中点电流的表达式在一个工频周期中改变6 次造成的；其次会有一定的直流分量和开关次谐波及其边带谐波，前者是由系统参数不对称引起的，后者是PWM 策略本身固有的特点。2）同相策略输出的相电压THD 略大于反相策略输出的相电压THD，这是由于同相策略输出相电压的谐波能量十分集中，大部分都在载波频率上，而反相策略输出相电压的谐波能量相对分散，以边带谐波为主；同相策略输出的线电压THD小于反相策略输出的线电压THD，这是由于在m为奇数时，反相策略输出线电压中的边带谐波距其中（载波奇数倍）点较近，谐波幅值大。

图6 载波同相层叠法的实验结果（M=0.8）Fig.6 Experimental results of PD-PWM（M=0.8）

图7 载波反相层叠法的实验结果（M=0.8）Fig.7 Experimental results of POD-PWM（M=0.8）

图8 载波同相交叠法的实验结果（M=0.8，V=1.6）Fig.8 Experimental results of CO-PWMA（M=0.8，V=1.6）

图9 载波反相交叠法的实验结果（M=0.8，V=1.6）Fig.9 Experimental results of CO-PWMB（M=0.8，V=1.6）

表3 4种策略输出相电压脉冲实验结果对比Tab.3 Output phase voltage experimental results of four kinds of carrier modulation strategy

表4 4种策略输出线电压脉冲实验结果对比Tab.4 Output line voltage experimental results of four kinds of carrier modulation strategy

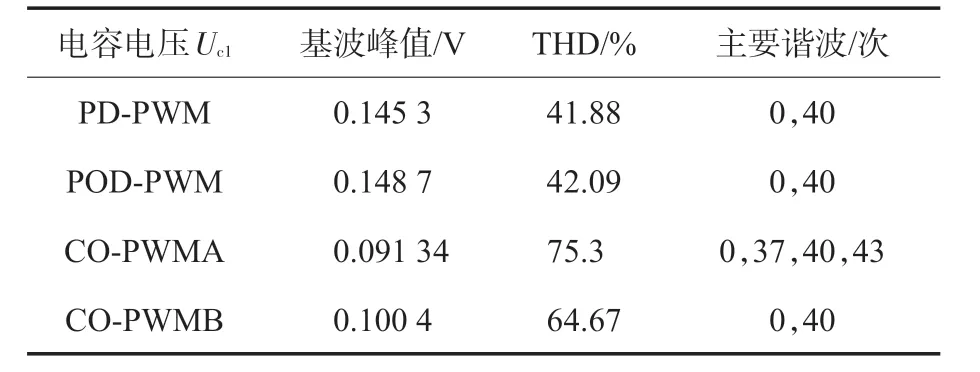
表5 4种策略中点电压波动实验结果对比Tab.5 NP voltage fluctuation experimental results of four kinds of carrier modulation strategy

表6 4种策略滤波后的线电压实验结果对比Tab.6 Output line voltage experimental results of four kinds of carrier modulation strategy（After filtering）

4 结论

本文研究了4 种三电平载波调制策略对中点电压的影响及其输出相电压和线电压的基波分量及谐波特性，通过本文的分析得到如下的结论：1）载波交叠策略比载波层叠策略具有更小的中点电压波动；2）载波交叠策略比载波层叠策略具有更高的直流电压利用率，但会引入较难滤除的低次谐波；3）在输出波形相电压THD特性方面，反相层叠策略小于同相层叠策略，反相交叠策略小于同相交叠策略；在输出波形线电压THD方面，反相层叠策略和反相交叠策略分别大于同相层叠策略和同相交叠策略。

［1］ Nabae A，Takahashi I，Akagi H.A New Neutral Point Clamped PWM Inverter［J］.IEEE Transaction on Industry Applications，1981，17（5）：518-523.

［2］ 谢桢，魏建勋，付立军，等.三电平H 桥直流换流器电流连续模式下的建模与控制器设计［J］.电网技术，2013，37（5）：1230-1236.

［3］ 谢小荣，严干贵，陈远华.三电平PWM 变频调速控制系统的MATLAB 仿真平台［J］.电网技术，2003，27（9）：18-22.

［4］ 贺昱曜，冯伟，宋石磊.Z 源级联三电平中点钳位逆变器［J］.电网技术，2012，36（4）：219-224.

［5］ 宋文祥，董英，阮智勇.电网电压不平衡时三电平整流器静止坐标系控制研究［J］.电网技术，2013，37（1）：94-99.

［6］ McGrath B P，Holmes D G.Multicarrier PWM Strategies for Multilevel Inverters［J］.IEEE Transaction on Industrial Electronics，2002，49（4）：858-867.

［7］ Holmes D，Lipo T.Pulse Width Modulation for Power Converters：Principles and Practice［C］//Wiley-IEEE Press，2003.

［8］ Zheng Hong，Zhu Baohua，Zhang Hanghui，et al.Carrier Overlaping-switch Frequency Optional PWM Method for Cascaded Multilevel Inverter［C］//International Conference on Electrical and Control Engineering，China，2010.

［9］ Shanthi B，Natarajan S P.Comparative Study on Carrier Overlapping PWM Strategies for Five Level Flying Capacitor Inverter［J］.International Journal of Sciences and Techniques of Automatic Control&Computer Engineering，2010，4（1）：1158-1173.

［10］Bensraj R，Natarajan S P，Padmathilagam V.Multicarrier Trapezoidal PWM Strategies Based on Control Freedom Degree for MSMI［J］.ARPN Journal of Engineering and Applied Sciences，2010，5（5）：32-41.

［11］张云，孙力，吴凤江，等.电容箝位型非对称H 桥五电平逆变器正弦脉宽调制控制［J］.中国电机工程学报，2009，29（21）：40-45.

［12］王鸿雁，张超，王小峰，等.基于控制自由度组合的多电平PWM 方法及其理论分析［J］.中国电机工程学报，2006，26（6）：42-48.

［13］王小峰，何湘宁，邓焰.载波交叠特性PWM 方法在飞跨电容多电平逆变器中的应用研究［J］.中国电机工程学报，2007，27（10）：98-102.

［14］赵慧杰，钱照明，李骏，等.载波PWM 方法三电平逆变器中点电位控制研究［J］.电力电子技术，2007，41（3）：28-30.

［15］胡存刚，王群京，李国立，等.基于虚拟空间矢量的三电平NPC 逆变器中点电压平衡控制方法［J］.电工技术学报，2009，24（5）：100-107.

［16］原熙博，李永东，王琛琛.基于零序分量注入的三电平PWM 整流器目标优化控制［J］.电工技术学报，2009，24（3）：116-121.

［17］Holmes D G，Thomas A L.Pulse Width Modulation for Power Converters：Principles and Practice［M］.Hoboken，NJ：Wiley-IEEE Press，2003：623-633.